全桥逆变里的180度导电角：揭开它的神秘面纱

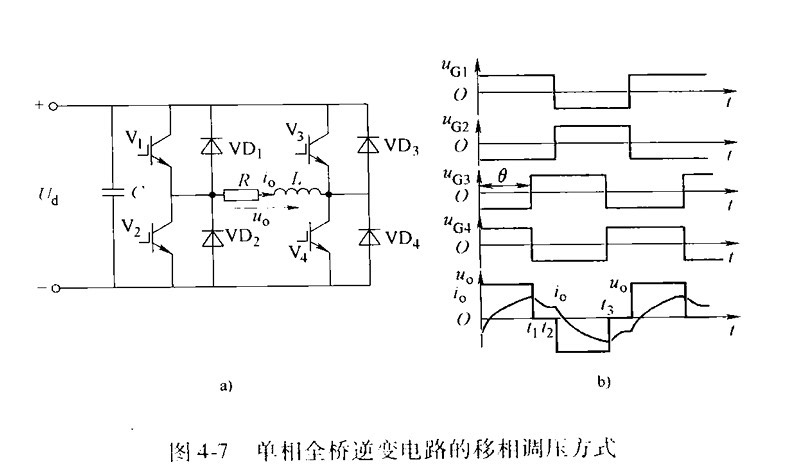
全桥逆变采用180度导电角度方式 Matlab仿真报告四个桥臂看作两个半桥组合而成，两对桥臂交替导通180度，在阻感负载时，还可以采用移相的方式调节输出电压，这种方式称为移相调压。

全桥逆变器是电力电子领域里的常客，而在全桥逆变中，180度导电角度的方式更是经常被提及的热门话题。让我来慢慢理清楚这其中的奥秘。

从结构说到180度导电

全桥逆变器，简单来说，就是由四个开关器件组成的桥式电路，这四个桥臂可以灵活组合，产生我们想要的输出波形。而当我们把这四个桥臂看作两个半桥组合时，就可以巧妙地利用它们的交替导通特性。

这里有个关键点：四个桥臂交替导通180度。这180度的意义在于，每个桥臂在一个开关周期内导通一半的时间，这样可以保证输出波形的对称性，同时也让各个开关器件的应力分布更加均匀。

我们来试着用Matlab仿真一下，看看这种180度导电方式的波形是怎样的：

matlab 复制代码

% 设置采样频率和时间步长
Fs = 10000;
t = 0:1/Fs:0.02;

% 设置开关频率和占空比
f = 500;
duty = 0.5;

% 生成PWM信号
PWM1 = sign(sin(2*pi*f*t));
PWM2 = -sign(sin(2*pi*f*t));

% 绘制波形图
figure;
plot(t, PWM1, 'b', 'LineWidth', 2);
hold on;
plot(t, PWM2, 'r', 'LineWidth', 2);
title('180度导电角度PWM波形');
 xlabel('时间（秒）');
 ylabel('电压（V）');
legend('桥臂1', '桥臂2');

从仿真波形中可以看出，两个桥臂的PWM信号严格对称，彼此相差180度。这种对称性正是全桥逆变器稳定运行的基础。

移相调压：阻感负载中的秘密武器

当我们面对阻感负载时，仅仅依靠导通角度可能无法完全满足调节需求。这时候，移相调压就登场了。

移相调压的基本思想是在全桥逆变的基础上，通过改变桥臂的导通相位来调节输出电压的幅度。这个相位差的大小直接影响输出电压的有效值。这种方法特别适合于需要平滑调压的应用场景。

让我用一个简单的例子来说明移相调压的原理。假设我们有一个阻感负载，其等效电路可以表示为一个电阻和一个电感串联。当改变桥臂的导通相位时，输出电压的波形会发生怎样的变化呢？

matlab 复制代码

% 设置相位差
phase_shift = 30; % 相位差以度为单位

% 将相位差转换为弧度
phase_shift_rad = phase_shift * pi / 180;

% 生成移相后的PWM信号
PWM1_shifted = sign(sin(2*pi*f*t));
PWM2_shifted = sign(sin(2*pi*f*t + phase_shift_rad));

% 绘制移相后的波形
figure;
plot(t, PWM1_shifted, 'b', 'LineWidth', 2);
hold on;
plot(t, PWM2_shifted, 'r', 'LineWidth', 2);
title('移相调压PWM波形');
xlabel('时间（秒）');
ylabel('电压（V）');
legend('桥臂1', '桥臂2');

从波形中可以看出，桥臂1和桥臂2之间的相位差已经改变，这会直接影响到输出电压的大小。

仿真中的几点收获

在Matlab仿真过程中，有几个地方让我印象深刻：

波形的对称性：严格的对称性是全桥逆变的基础，任何微小的偏差都会导致输出波形的畸变。
相位差的影响：移相调压的效果非常直观，相位差越大，输出电压的变化越明显。
开关器件的应力：180度导电方式确保了开关器件的应力分布更加均匀，这对实际应用中的可靠性非常重要。

通过这次仿真，我对全桥逆变器的工作原理和调压方法有了更深刻的理解。

在电力电子的世界里，每一个波形都蕴含着智慧的设计和巧妙的构思。全桥逆变器的180度导电方式，就是其中最经典的设计之一。希望这篇博文能为你理解全桥逆变器提供一些思路和帮助。