在4*∞的矩形空间内,按照从上到下,从左到右,最近取点法画函数y=2a2+1的图像

这个图像可以分成3部分

其中第1,3部分分布规律相对清晰
|-----|------|------|-----|----|----|----|-----|-----|-----|-----|----|----|-----|-----|-----|----|----|----|----|----|----|----|----|----|----|----|----|----|----|----|----|----|----|----|----|----|----|----|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 |
| 275 | 198 | 34 | 275 | 65 | 26 | 26 | 103 | 103 | 103 | 103 | 17 | 17 | 17 | 17 | 5 | 7 | 7 | 7 | 9 | 9 | 6 | 9 | 9 | 7 | 7 | 9 | 9 | 7 | 7 | 9 | 9 | 9 | 9 | 12 | 12 | 12 | 12 | 8 |
| 658 | 2801 | 263 | 40 | 40 | 40 | 40 | 85 | 85 | 85 | 49 | 49 | 49 | 49 | 103 | 103 | 5 | 9 | 9 | 6 | 6 | 7 | 7 | 7 | 7 | 7 | 7 | 7 | 7 | 9 | 9 | 9 | 9 | 7 | 7 | 7 | 7 | 7 | 7 |
| 26 | 13 | 2801 | 658 | 26 | 40 | 40 | 49 | 49 | 49 | 49 | 85 | 85 | 85 | 103 | 7 | 7 | 7 | 7 | 9 | 9 | 6 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 7 | 7 | 7 | 7 | 7 | 7 | 7 | 7 | 12 | 12 |
| 65 | 18 | 198 | 275 | 26 | 26 | 65 | 103 | 103 | 17 | 17 | 17 | 17 | 103 | 17 | 17 | 17 | 17 | 9 | 9 | 7 | 7 | 7 | 7 | 7 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 7 | 7 | 9 | 9 | 8 | 8 | 8 |
中间第2部分看似混乱,但仍然可以发现对称状结构。如果认为y=2a2+1的图像就是卡门涡街,那就相当于假设由层流到湍流的过渡就是两股流体搅到一起。这个假设能解释雷诺数吗?
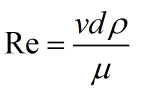
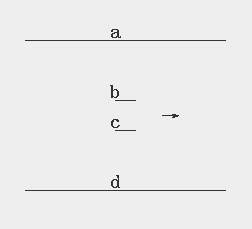
有一个圆管ad,这里假设管内液体分子呈片状存在,因为近中心处速度最大,设中心处有两个片状结构b和c,
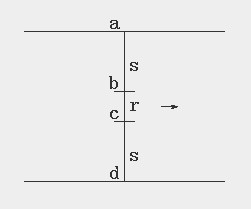
设b距上管壁的距离是s,bc的距离是r,c距下管壁的距离为s。因为分子尺度的r要远远小于s。因此2s≈管内径d。
考虑牛顿内摩擦定律
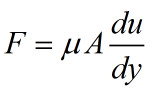
其中 μ 是动力粘度,A 是面积,u是相对速度,y 是平板间距
在运动中设c相对b静止,片层b 移动,
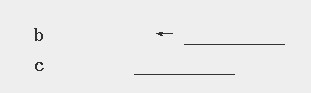
并产生摩擦力,这个摩擦力平行于b,在b和a之间还有多个片,b与这些片之间同样产生摩擦力,并最终将bc之间的摩擦力传导到a。就像c拉绳子,最终力总会作用到墙壁。所以A就是片的面积,V是b片的速度, c与a的距离为y=s+r约为S。
同样如果设b静止,c运动,结论一致,b和c之间的摩擦力最终都传导到对面的管壁。
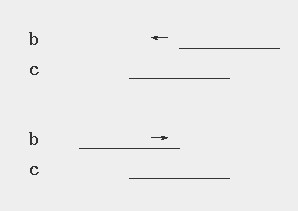
b相对c做往复运动,这个效果就像b在绕着c旋转,因此设
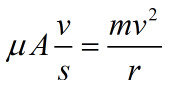
m是分子片的质量
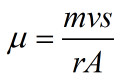
化简得到分子片的动力粘度
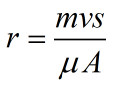
分子片的间距
现在假设分子片的厚度是h
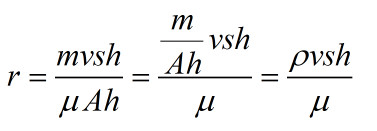
等式右侧上下乘h,所以Ah就是体积
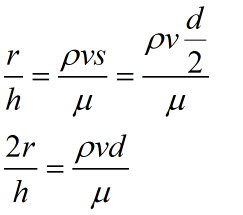
因为s为内径的一半,所以得到ρvd/μ=2r/h。r是距离,h是厚度,二者单位一致,因此2r/h是一个无量纲的量。