本文主要记录笔者备战蓝桥杯的记录。
前言
本文主要记录笔者备战蓝桥杯第二天的过程,包含一道基础题和一道进阶题。
一、基础题:拼接平方数
我先把题目测试链接粘贴在下面:
P8615 [蓝桥杯 2014 国 C] 拼接平方数 - 洛谷
题目详细叙述如下:
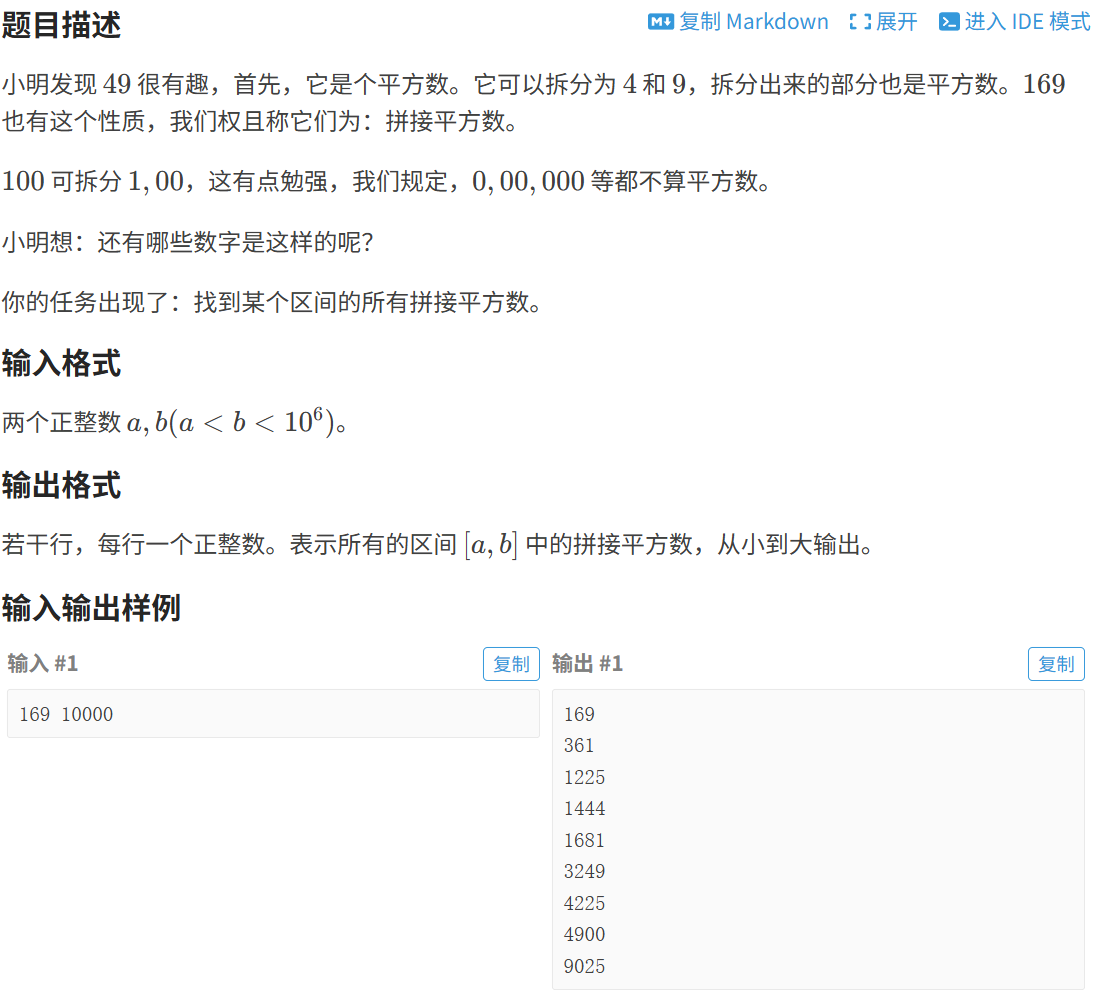
我的思路是首先,通过scanf函数读取用户输入的区间上下限a和b,确定后续需要遍历检查的数字范围。接着,用for循环遍历区间内的每一个整数n,对每个n都先进行第一层关键校验------判断其本身是否为平方数。这里采用的校验方式是通过sqrt函数计算n的平方根,将结果强制转换为整数得到root,再通过计算root的平方是否等于n来验证,若不相等,则说明n不符合基础条件,直接跳过对该数的后续处理,进入下一个数字的检查。 在确认n是平方数后,代码开始处理数字拆分的核心步骤。这里引入了divisor变量,初始值设为10,并且每次循环都会乘以10,其作用是作为数字拆分的位数分隔标识。通过整数除法n / divisor得到数字的高位部分left,通过取余运算n % divisor得到数字的低位部分right,这种拆分方式会按不同位数对n进行分割,比如对于三位数,divisor=10时拆成百位和后两位,divisor=100时拆成前两位和个位。 拆分完成后,代码会对left和right进行双重验证,首先确保两者都为非零值,避免出现无效的拆分结果,随后沿用之前验证平方数的方法,分别计算left和right的平方根并取整,通过平方验证判断它们是否为平方数。一旦找到一组符合条件的left和right,就将标记变量found设为1,立即跳出拆分循环,避免重复验证,并打印当前的数字n。我的代码如下:
cpp
#include <stdio.h>
#include <math.h>
int main() {
int a, b;
scanf("%d %d", &a, &b);
for (int n = a; n <= b; n++) {
int root = (int)sqrt(n);
if (root * root != n) continue;
int found = 0;
for (int divisor = 10; divisor < n; divisor *= 10) {
int left = n / divisor;
int right = n % divisor;
if (left > 0 && right > 0) {
int left_ = (int)sqrt(left);
int right_ = (int)sqrt(right);
if (left_ * left_ == left && right_ * right_ == right) {
found = 1;
break;
}
}
}
if (found) printf("%d\n", n);
}
return 0;
}
二、进阶题:排列数
我先把题目测试链接粘贴在下面:
题目详细叙述如下:

本题涉及到了动态规划,我目前还没有学习到,还是问了AI。它是这么说的,这段C语言代码是一个基于动态规划的组合计数工具,核心目标是计算特定规模与状态下的合法情况总数,并对结果取123456的模。它通过规模递增的方式,利用状态转移规则逐步推导结果,适用于解决"规模可拆分、状态可传递"的计数问题,比如特定约束下的排列组合、结构生成等场景。 代码的核心是二维数组dp,其中dp[i][j]代表问题规模为i时处于状态j的合法情况数量,第一维i对应问题的核心规模(如元素个数、结构长度等),第二维j对应具体的状态标识(如特征计数、匹配次数等)。为了避免内存中的脏数据影响计算,代码一开始就用memset函数将dp数组全部初始化为0,随后进行关键的初始化赋值:当规模为1时,只有状态0存在1种合法情况,即dp[1][0] = 1,这是整个计算的基础起点;而当规模i大于等于2时,状态0的合法情况数固定为2,即dp[i][0] = 2,这应该是问题本身约束下的固定基础情况。 状态转移是代码的核心计算环节,它遵循"从规模i推导规模i+1"的逻辑,通过三种不同的路径实现状态的更新。第一种路径是规模增加后状态保持不变,dp[i+1][j]会累加dp[i][j]乘以(j+1)的结果,这里的(j+1)对应这种转移方式下的可选方案数;第二种路径是规模增加后状态变为j+1,累加的是dp[i][j]乘以2的结果,意味着这种转移有2种固定选择;第三种路径是状态变为j+2,累加的是dp[i][j]乘以(i - j - 2)的结果,该系数与当前的规模i和状态j直接相关,反映了不同条件下可选方案的差异。每一步累加后都会通过mod函数取模123456,既能满足题目对结果的要求,又能有效避免整数累加导致的溢出问题,确保计算过程的稳定性。 使用这段代码时需要注意几个关键限制:数组dp的最大尺寸定义为505,这意味着输入的n值不能超过504,否则会出现数组越界的错误;输入的k值需要保证k-1不超过n的范围,否则dp[n][k-1]会默认取0,即无合法情况;代码未对输入的n和k做合法性校验,使用时需自行确保输入数据符合上述范围要求,避免运行异常。代码如下:
cpp
#include <stdio.h>
#include <string.h>
#define MOD 123456
#define MAX_SIZE 505
// 取模函数(确保结果非负且在MOD范围内)
int mod(int a) {
return a % MOD;
}
int main() {
int n, k;
int dp[MAX_SIZE][MAX_SIZE];
// 初始化dp数组为0,避免脏数据影响
memset(dp, 0, sizeof(dp));
// 读取输入n和k
scanf("%d %d", &n, &k);
// 动态规划初始化
dp[1][0] = 1; // 规模为1时,状态j=0的数量为1
for (int i = 2; i < n; i++) {
dp[i][0] = 2; // 规模≥2时,状态j=0的数量固定为2
for (int j = 0; j <= i; j++) {
// 状态转移:从规模i转移到规模i+1,更新不同j值的状态数
dp[i+1][j] = mod(dp[i+1][j] + mod(dp[i][j] * (j + 1)));
dp[i+1][j+1] = mod(dp[i+1][j+1] + mod(dp[i][j] * 2));
dp[i+1][j+2] = mod(dp[i+1][j+2] + mod(dp[i][j] * (i - j - 2)));
}
}
// 输出结果:规模为n、状态为k-1的数量,取模MOD
printf("%d\n", mod(dp[n][k-1]));
return 0;
}
总结
本文记录了蓝桥杯备赛过程,包含两道编程题解析。基础题"拼接平方数"通过遍历区间数字,验证其是否为平方数并能拆分为两个平方数之和。进阶题"排列数"采用动态规划方法,使用二维数组存储状态,通过三种转移路径计算特定规模的合法排列数,并对结果取模。文章展示了算法实现思路和关键代码片段,体现了从基础到进阶的解题过程。