本文主要记录笔者备战蓝桥杯的过程。
目录
前言
本文主要记录笔者备战蓝桥杯的过程,包括一道基础题和一道进阶题。
一、基础题:刷题统计
我先把题目测试链接粘贴在下面:
P8780 [蓝桥杯 2022 省 B] 刷题统计 - 洛谷
题目详细叙述如下:
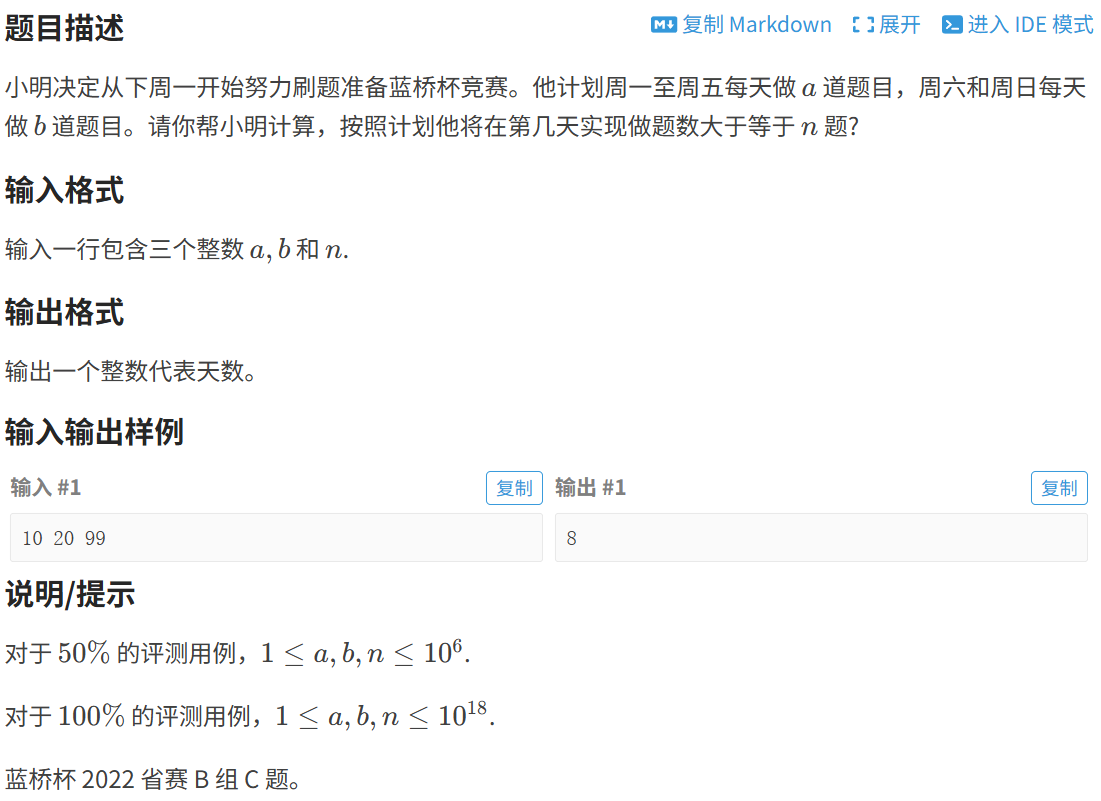
我的核心思路是先整后零计算消耗完总量n的总天数,先根据每周前5天每天消耗a、后2天每天消耗b的规则,算出单周总消耗5*a + 2*b,通过整数除法得到能完整消耗的周数weeks,并从n中扣除这些整周的消耗量,再遍历一周7天,按前5天扣a、后2天扣b的规则逐天处理剩余的n,统计不足一周的消耗天数days,最终总天数为7*weeks + days,代码如下:
cpp
#include <stdio.h>
int main(){
long long a = 0;
long long b = 0;
long long n = 0;
scanf("%lld %lld %lld", &a, &b, &n);
long long weeks = n / (5 * a + 2 * b);
n -= (weeks * (5 * a + 2 * b));
int days = 0;
for(int i = 0; i < 7; i++){
if(n > 0){
if(i < 5){
n -= a;
}else{
n -= b;
}
days++;
}else{
break;
}
}
printf("%lld", 7 * weeks + days);
}
二、进阶题:选素数
我先把题目测试链接粘贴在下面:
题目详细叙述如下:
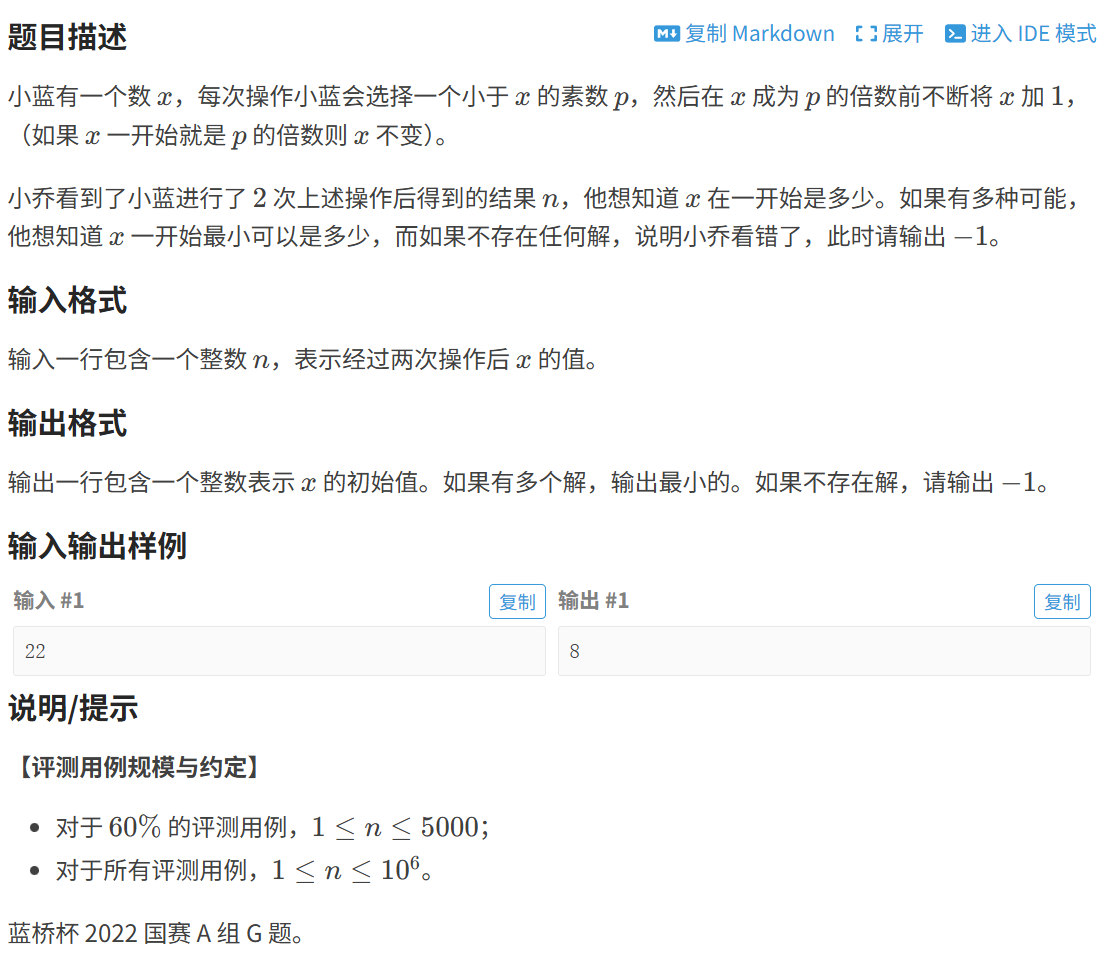
核心思路是反向推导+素因数限定范围+最小化验证,首先明确选小于当前数的素数p,补到p的倍数的操作逻辑,反向来看,若操作结果是res,则操作前的数需在(res-p, res]之间(且p是res的素因数、p小于操作前的数)。解题时,先从最终结果n出发,找出n的所有素因数(作为第二次操作的候选素数p1),据此确定第二次操作前数y的合法范围(需满足y>p1且y∈(n-p1, n]),遍历这些y并验证其选p1操作后是否得到n;再对每个合法的y,找出y的所有素因数(作为第一次操作的候选素数p2),确定第一次操作前数x的合法范围(需满足x>p2且x∈(y-p2, y]),遍历x验证其选p2操作后是否得到y,过程中记录最小的x;最终若找到最小x则输出,无合法值则输出-1。代码如下:
cpp
#include <stdio.h>
#include <limits.h>
#include <stdbool.h>
// 计算两个数的最大值(long long类型)
long long max(long long a, long long b) {
return a > b ? a : b;
}
// 判断一个数是否为素数
bool is_prime(long long num) {
if (num < 2) return false;
if (num == 2) return true;
if (num % 2 == 0) return false;
for (long long i = 3; i * i <= num; i += 2) {
if (num % i == 0) return false;
}
return true;
}
// 获取一个数的所有不同素因数(存到factors数组,count为因数数量)
void get_prime_factors(long long num, long long factors[], int *count) {
*count = 0;
if (num < 2) return;
// 处理素因数2
if (num % 2 == 0) {
factors[(*count)++] = 2;
while (num % 2 == 0) num /= 2;
}
// 处理奇数素因数
for (long long i = 3; i * i <= num; i += 2) {
if (num % i == 0) {
factors[(*count)++] = i;
while (num % i == 0) num /= i;
}
}
// 剩余的数本身是素因数
if (num > 1) factors[(*count)++] = num;
}
// 模拟单次操作:num选素数p后得到的结果
long long get_oper_result(long long num, long long p) {
if (p >= num || !is_prime(p)) return -1; // 非法输入(p不满足条件)
// 计算≥num的最小p的倍数:(num + p - 1)/p 是向上取整的结果
return (num + p - 1) / p * p;
}
int main() {
long long n;
scanf("%lld", &n);
long long min_x = LLONG_MAX; // 初始化最小x为极大值
long long n_factors[100]; // 存储n的素因数
int n_factor_count = 0;
get_prime_factors(n, n_factors, &n_factor_count);
// 遍历n的每个素因数(作为第二次操作的p1)
for (int i = 0; i < n_factor_count; i++) {
long long p1 = n_factors[i];
// 计算第二次操作前y的合法范围:(n-p1, n] 且 y > p1
long long y_start = max(p1 + 1, n - p1 + 1);
long long y_end = n;
if (y_start > y_end) continue; // 无合法y,跳过
// 遍历所有可能的y
for (long long y = y_start; y <= y_end; y++) {
// 验证y经过p1操作是否得到n
if (get_oper_result(y, p1) != n) continue;
// 获取y的所有素因数(作为第一次操作的p2)
long long y_factors[100];
int y_factor_count = 0;
get_prime_factors(y, y_factors, &y_factor_count);
if (y_factor_count == 0) continue;
// 遍历y的每个素因数p2,找第一次操作的x
for (int j = 0; j < y_factor_count; j++) {
long long p2 = y_factors[j];
// 计算第一次操作前x的合法范围:(y-p2, y] 且 x > p2
long long x_start = max(p2 + 1, y - p2 + 1);
long long x_end = y;
if (x_start > x_end) continue;
// 遍历x找最小合法值
for (long long x = x_start; x <= x_end; x++) {
if (get_oper_result(x, p2) == y) {
if (x < min_x) {
min_x = x;
}
break; // x从小到大遍历,第一个即为当前p2下的最小x
}
}
}
}
}
// 输出结果
if (min_x == LLONG_MAX) {
printf("-1\n");
} else {
printf("%lld\n", min_x);
}
return 0;
}
总结
本文主要记录笔者备战蓝桥杯的过程,包括一道基础题和一道进阶题的讲解。