本文主要记录笔者蓝桥杯备战过程
目录
前言
本文记录笔者备战蓝桥杯第三天的过程,包括一道基础题和一道进阶题。
一、基础题:乘法表
我先把题目测试链接粘贴在下面:
P8723 [蓝桥杯 2020 省 AB3] 乘法表 - 洛谷
题目详细叙述如下:
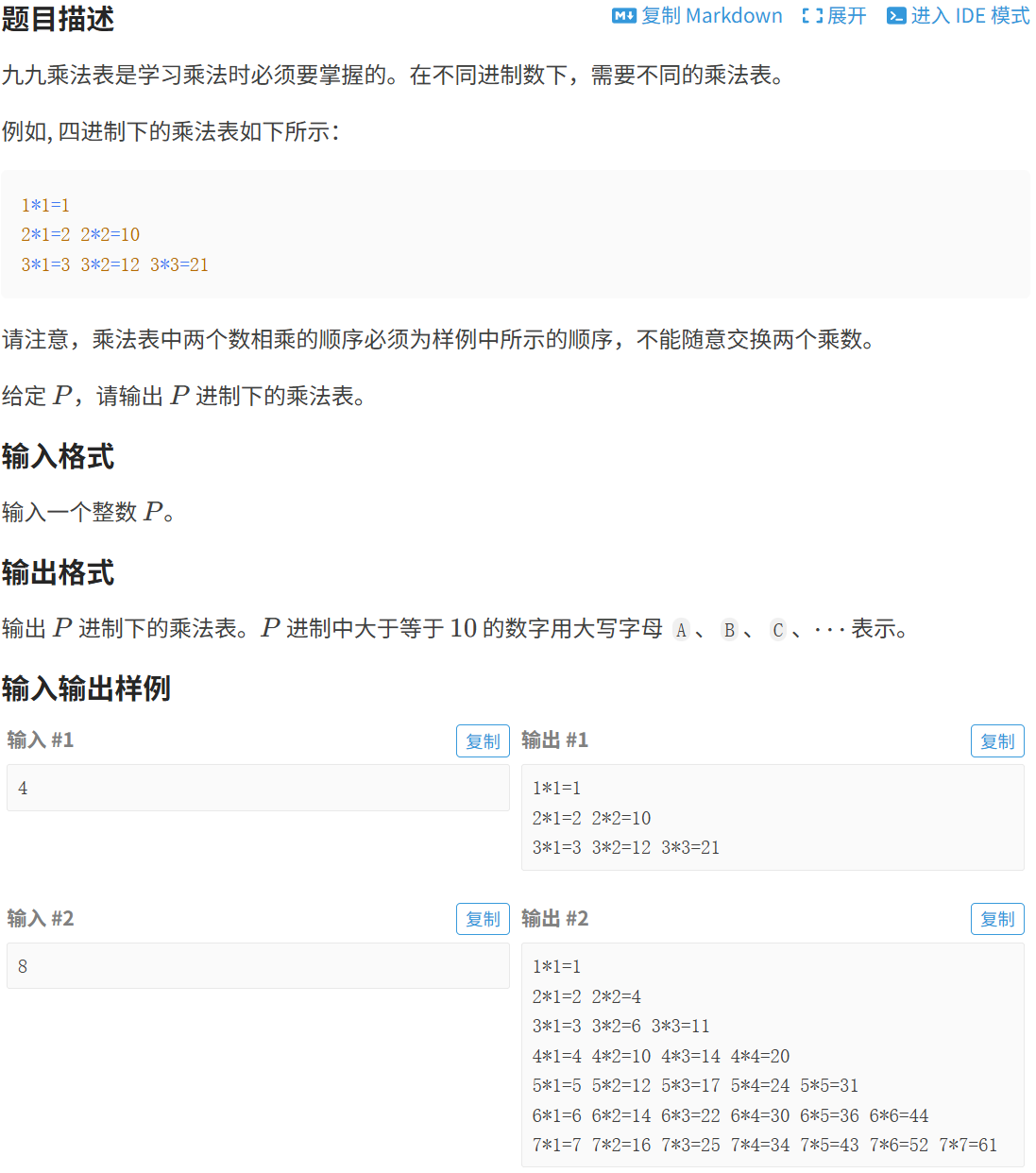
我的思路是通过signal数组建立0-9、A-Z与0-35的直接映射,以双重上三角循环(i从1到p-1、j从1到i)生成乘数组合,先计算十进制乘积sum,再根据sum是否小于p判断其p进制为1位或2位,分别通过signal数组索引取值存入tmp数组,最终按p进制乘数*p进制乘数=p进制乘积的格式输出,且仅在非行尾式子后加空格,形成无多余空格、布局整齐的p进制乘法表。我的代码如下:
cpp
#include <stdio.h>
#include <stdlib.h>
int main(){
int p = 0;
scanf("%d", &p);
char* signal = "0123456789ABCDEFGHIJKLMNOPQRSTUVWXYZ";
for(int i = 1; i < p; i++){
for(int j = 1; j <= i; j++){
char tmp[3] = {0};
int sum = i * j;
if(sum < p){
tmp[0] = signal[sum];
}else{
tmp[1] = signal[sum % p];
tmp[0] = signal[sum / p];
}
printf("%c*%c=%s", signal[i], signal[j], tmp);
if (j != i) {
printf(" ");
}
}
printf("\n");
}
return 0;
}
二、进阶题:奇偶覆盖
我先把题目测试链接粘贴在下面:
P8734 [蓝桥杯 2020 国 A] 奇偶覆盖 - 洛谷
题目详细叙述如下:
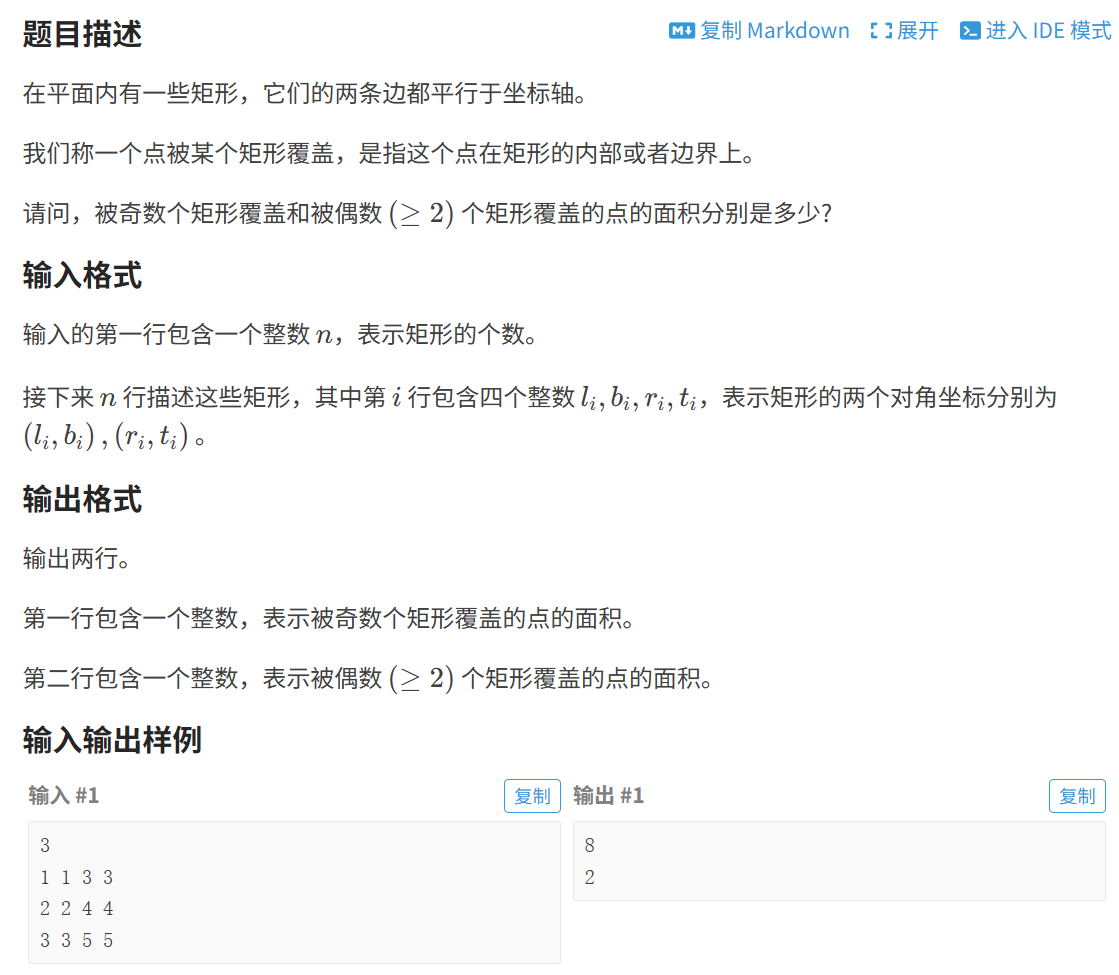
这道题则是涉及到了扫描线和线段树,我问了下AI,它是这么做的,将每个矩形拆分为上下两条水平边界扫描线(上边界标记添加覆盖,下边界标记删除覆盖),按y坐标升序排序扫描线;对所有矩形的x坐标离散化,构建线段树维护x轴区间的覆盖次数,实时计算当前y区间内奇数覆盖次数的长度和≥2次偶数覆盖次数的长度;扫描线从下到上移动,每次用当前有效长度乘以扫描线移动的高度差,分别累加得到两类覆盖面积,最终输出结果,时间复杂度O (nlogn),适用于大数据量场景。代码如下:
cpp
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#define ll long long
#define N 1000005
#define lson p<<1
#define rson p<<1|1
// 扫描线结构体(存储x区间、y坐标、标记:添加1/删除-1)
typedef struct Line {
ll l, r, h;
int mark;
} Line;
// 线段树结构体(维护x轴区间的覆盖状态)
typedef struct segment_tree {
ll l, r; // 对应X数组的左右索引(实际坐标通过X数组映射)
ll len1, len2; // len1:奇数覆盖次数的长度;len2:≥2次偶数覆盖次数的长度
int sum; // 区间覆盖次数
} segment_tree;
// 全局变量(避免函数传参冗余,适配线段树全局存储)
segment_tree t[N << 2]; // 线段树数组(4倍空间)
Line line[N << 1]; // 扫描线数组(2n个边界)
ll X[N << 1]; // 存储所有x坐标(用于离散化)
ll ans1, ans2; // 结果:ans1=奇数覆盖面积,ans2=≥2次偶数覆盖面积
ll n; // 矩形个数(最终会变成2n,存储扫描线数量)
// 快速读入函数(C语言实现,兼容大数字)
void read(ll *a) {
char ch;
int f = 1;
ll k = 0;
ch = getchar();
while (ch < '0' || ch > '9') {
if (ch == '-') f = -1;
ch = getchar();
}
while (ch >= '0' && ch <= '9') {
k = k * 10 + ch - '0';
ch = getchar();
}
*a = k * f;
}
// qsort比较函数:扫描线按y坐标升序排序
int cmp_line(const void *x, const void *y) {
Line *a = (Line *)x;
Line *b = (Line *)y;
return a->h < b->h ? -1 : 1;
}
// qsort比较函数:x坐标升序排序(用于离散化)
int cmp_x(const void *x, const void *y) {
ll *a = (ll *)x;
ll *b = (ll *)y;
return *a < *b ? -1 : 1;
}
// 去重函数:对排序后的X数组去重,返回去重后长度
int unique(ll *arr, int len) {
int tot = 1;
for (int i = 2; i <= len; i++) {
if (arr[i] != arr[tot]) {
arr[++tot] = arr[i];
}
}
return tot;
}
// 线段树push_up:更新当前节点的len1和len2(核心逻辑)
void push_up(int p) {
if (t[p].sum == 0) { // 无覆盖,继承左右子节点的长度
t[p].len1 = t[lson].len1 + t[rson].len1;
t[p].len2 = t[lson].len2 + t[rson].len2;
} else if (t[p].sum % 2 == 0) { // 偶数次覆盖(≥2)
t[p].len1 = t[lson].len1 + t[rson].len1; // 奇数长度继承子节点
t[p].len2 = X[t[p].r] - X[t[p].l] - t[p].len1; // 总长度 - 奇数长度 = 偶数≥2长度
} else { // 奇数次覆盖
t[p].len2 = t[lson].len1 + t[rson].len1; // 子节点奇数长度变为当前偶数≥2长度
t[p].len1 = X[t[p].r] - X[t[p].l] - t[p].len2; // 总长度 - 偶数≥2长度 = 奇数长度
}
}
// 线段树构建:初始化区间[l, r](基于X数组的索引)
void build(int p, int l, int r) {
t[p].l = l;
t[p].r = r;
t[p].sum = 0;
t[p].len1 = 0;
t[p].len2 = 0;
if (l + 1 == r) { // 叶子节点(对应X[l]到X[r]的区间)
return;
}
int mid = (l + r) >> 1;
build(lson, l, mid);
build(rson, mid, r);
}
// 线段树修改:对x轴区间[L, R]添加覆盖标记w(1=添加,-1=删除)
void modify(int p, ll L, ll R, int w) {
// 区间无交集,直接返回
if (X[t[p].r] <= L || X[t[p].l] >= R) {
return;
}
// 完全覆盖当前节点的x区间,更新sum并push_up
if (L <= X[t[p].l] && X[t[p].r] <= R) {
t[p].sum += w;
push_up(p);
return;
}
// 递归修改左右子节点
modify(lson, L, R, w);
modify(rson, L, R, w);
push_up(p); // 回溯更新当前节点
}
int main() {
read(&n);
ll xa, xb, ya, yb;
for (ll i = 1; i <= n; i++) {
read(&xa);
read(&ya);
read(&xb);
read(&yb);
// 收集所有x坐标(用于离散化)
X[2 * i - 1] = xa;
X[2 * i] = xb;
// 拆分矩形为上下边界扫描线:上边界(y=ya)添加,下边界(y=yb)删除
line[2 * i - 1] = (Line){xa, xb, ya, 1};
line[2 * i] = (Line){xa, xb, yb, -1};
}
n <<= 1; // 扫描线总数=2*原矩形数
// 排序:扫描线按y升序,x坐标按升序(用于离散化)
qsort(line + 1, n, sizeof(Line), cmp_line);
qsort(X + 1, n, sizeof(ll), cmp_x);
// x坐标离散化(去重),得到有效x区间数量
int tot = unique(X, n);
// 构建线段树(基于离散化后的x索引)
build(1, 1, tot);
// 扫描线遍历:从下到上处理每个y区间
for (ll i = 1; i < n; i++) {
// 修改当前扫描线对应的x区间覆盖状态
modify(1, line[i].l, line[i].r, line[i].mark);
// 累加面积:当前有效长度 × 扫描线移动的高度差(line[i+1].h - line[i].h)
ans1 += t[1].len1 * (line[i + 1].h - line[i].h);
ans2 += t[1].len2 * (line[i + 1].h - line[i].h);
}
// 输出结果
printf("%lld\n%lld\n", ans1, ans2);
return 0;
}
总结
本文记录了蓝桥杯备战的第三天学习内容,包括一道基础题和一道进阶题的解题过程。基础题"乘法表"通过建立字符映射和双重循环实现了p进制乘法表的生成。进阶题"奇偶覆盖"则运用了扫描线算法和线段树技术,通过离散化处理和区间维护计算了奇数覆盖和偶数覆盖的面积。两题分别展示了基础编程能力和高级算法应用,体现了从简单到复杂的编程思维训练过程。