探索质心侧偏角 - 质心侧偏角速度相平面

质心侧偏角-质心侧偏角速度相平面(sideslip angle phase plane) 质心侧偏角-质心侧偏角速度相平面程序，其中包括相平面绘制，鞍点绘制，双线法边界绘制及公式E1和E2的计算与拟合。已一键出图，包括斜率计算，带自编说明文档和双线法拟合数据。

最近捣鼓了一个超有趣的玩意儿 - 质心侧偏角 - 质心侧偏角速度相平面程序，跟大家分享分享。

相平面在动力学分析里那可是相当重要的工具，它能直观呈现系统状态随时间的变化。在我们这个场景下，质心侧偏角和质心侧偏角速度的相平面，对于理解车辆动力学等相关系统的行为特性有极大帮助。

相平面绘制

咱先来看相平面绘制部分的代码，以Python为例：

python 复制代码

import numpy as np
import matplotlib.pyplot as plt

# 假设我们已经有质心侧偏角alpha和质心侧偏角速度r的数据
alpha = np.linspace(-np.pi/4, np.pi/4, 100)
r = np.sin(alpha)

plt.plot(alpha, r)
plt.xlabel('质心侧偏角 ($\alpha$)')
plt.ylabel('质心侧偏角速度 ($r$)')
plt.title('质心侧偏角 - 质心侧偏角速度相平面')
plt.grid(True)
plt.show()

这里简单地生成了一些模拟数据（实际应用肯定是从传感器或复杂模型获取真实数据啦），然后用 matplotlib 库绘制相平面。np.linspace 生成了质心侧偏角的范围，np.sin(alpha) 模拟了质心侧偏角速度和质心侧偏角的关系（实际关系复杂得多）。plt.plot 绘制两者关系，xlabel、ylabel 和 title 分别给图表加上合适的标签和标题，grid(True) 显示网格，最后 show() 展示图形。

鞍点绘制

找到鞍点对于分析系统的稳定性等特性很关键。假设我们有一个函数来判断鞍点（实际计算鞍点要根据系统的具体动力学方程）：

python 复制代码

def find_saddle_point(alpha, r):
    # 这里简单假设鞍点是数据中间点，实际要根据具体算法找
    index = len(alpha) // 2
    return alpha[index], r[index]

saddle_alpha, saddle_r = find_saddle_point(alpha, r)
plt.scatter(saddle_alpha, saddle_r, color='red', label='鞍点')
plt.legend()

这段代码里，findsaddlepoint 函数很简陋地以数据中间点当作鞍点（实际肯定得按系统动力学方程来精确计算）。然后用 scatter 函数把鞍点标在相平面上，红色点，还加了个标签说明这是鞍点。

双线法边界绘制及公式E1和E2的计算与拟合

双线法边界绘制以及E1、E2公式的计算拟合是重头戏。下面假设我们有两个函数来计算E1和E2：

python 复制代码

def calculate_E1(alpha, r):
    # 这里假设简单公式 E1 = alpha + r
    return alpha + r

def calculate_E2(alpha, r):
    # 这里假设简单公式 E2 = alpha - r
    return alpha - r

E1 = calculate_E1(alpha, r)
E2 = calculate_E2(alpha, r)

# 这里假设拟合双线（实际要复杂的拟合算法）
fit_line1 = np.polyfit(alpha, E1, 1)
fit_line2 = np.polyfit(alpha, E2, 1)
fit_fn1 = np.poly1d(fit_line1)
fit_fn2 = np.poly1d(fit_line2)

plt.plot(alpha, fit_fn1(alpha), label='拟合E1线')
plt.plot(alpha, fit_fn2(alpha), label='拟合E2线')
plt.legend()

在这段代码里，calculateE1**和 calculate E2 简单假设了计算公式（实际根据系统物理原理确定）。接着计算出E1和E2的值，然后用 np.polyfit 进行一阶多项式拟合，np.poly1d 创建拟合函数，最后把拟合线也画在相平面上。

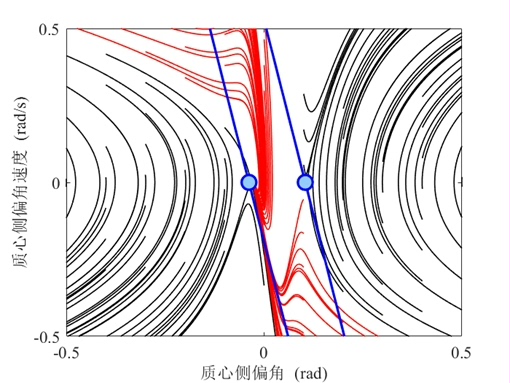
这次已一键出图，还包括斜率计算，而且带了自编说明文档和双线法拟合数据。整个过程不仅能加深对车辆动力学等相关系统的理解，代码实现过程也很有趣，大家不妨自己动手试试，说不定能发现更多有意思的东西。