通用图像融合方法利用梯度迁移学习与融合规则展开
A General Image Fusion Approach Exploiting Gradient Transfer Learning and Fusion Rule Unfolding
作者: Wu Wang, Liang-Jian Deng, Qi Cao, Gemine Vivone
发表期刊: IEEE TRANSACTIONS ON PATTERN ANALYSIS AND MACHINE INTELLIGENCE
论文地址: https://ieeexplore.ieee.org/document/11359013
摘要
基于深度学习的通用图像融合方法的目标是通过单一模型解决多种图像融合任务,从而促进模型在实际应用中的部署。然而,现有方法在模型训练和网络设计两个层面上均未能提供高效且全面的解决方案。在模型训练方面,现有方法无法有效利用不同任务之间的互补信息;在网络设计方面,则主要依赖经验驱动的网络结构设计。为了解决上述问题,本文提出了一种综合性的通用图像融合框架,结合了新提出的梯度迁移学习与融合规则展开。在训练阶段,为了充分利用不同任务之间的互补信息,我们基于这样一个思想提出了一种序列式梯度迁移框架:不同的图像融合任务往往包含互补的结构细节,而图像梯度能够有效表征这些细节。在网络设计方面,为了摆脱启发式设计的限制,我们演化出一种基础的图像融合规则,并将其融入深度平衡模型中,从而构建了一种更加高效且通用的图像融合网络,能够统一处理多种融合任务。针对三种不同的图像融合任务,即多聚焦图像融合、多曝光图像融合以及红外与可见光图像融合,所提出的方法不仅生成了具有更丰富结构信息的融合图像,而且在客观评价指标上也取得了极具竞争力的性能。此外,在此前未见过的图像融合任务(即医学图像融合)上的泛化实验结果表明,本文方法显著优于现有对比方法。代码将在可能接收后公开。
关键词---图像融合,通用学习框架,梯度迁移学习,融合规则展开,多聚焦图像融合,多曝光图像融合,红外与可见光图像融合。
1 引言

成像传感器由于物理限制,只能捕获场景的特定部分。图像融合算法旨在通过融合来自不同源图像的信息,生成一幅综合输入数据优势的单一图像,从而克服这些限制。本文聚焦于针对典型图像融合任务而设计的图像融合算法,包括多聚焦图像融合(MFIF)、多曝光图像融合(MEIF)、红外与可见光图像融合(IVF)以及医学图像融合(MIF)。其示意图如图 1 所示。
传统的图像融合方法通过手工设计的特征和融合规则来生成融合结果。其中,基于变换的图像融合方法由于能够建模多种图像融合方式而得到了广泛研究。典型的变换包括小波变换和非下采样轮廓波变换。这些方法虽然具有较好的可解释性并能够利用领域知识,但在刻画有效图像融合所需的非线性关系方面存在不足,因此其性能往往受到限制。
得益于其强大的表示能力,深度学习(DL)方法已成为图像融合研究中的重要方向。基于 DL 的图像融合方法可分为非通用方法和通用方法。由于非通用图像融合方法只能解决单一的图像融合任务,近年来的研究重点转向了能够通过单一模型解决多种图像融合任务的通用图像融合方法。尽管取得了一定进展,现有的通用图像融合方法在模型训练和网络设计两个方面仍未能提供高效且全面的解决方案。
在模型训练方面,大多数方法采用任务特定学习或多任务学习策略。任务特定学习为每个任务使用相同的神经网络分别训练独立模型,但该方法无法利用任务之间的信息。为了解决这一问题,U2Fusion 和 TCMOE 采用多任务学习从多种图像融合数据中进行学习。然而,多任务学习方法面临任务冲突问题,这会导致模型在某些任务上的性能下降。例如,在 MEIF 任务中,源图像可能包含欠曝光或过曝光区域,融合图像需要呈现正常曝光;而在 MFIF 任务中,则要求融合图像保持源图像的曝光特性。因此,MEIF 任务与 MFIF 任务的目标存在冲突,使得基于多任务学习的方法难以在多种图像融合任务上同时取得理想性能。综上所述,任务特定方法无法利用跨任务信息,而多任务学习方法又受到任务冲突的限制,从而影响整体效果。
在网络设计方面,现有基于 DL 的通用图像融合方法通常依赖经验进行网络结构设计,这一过程往往耗时且难以解释。例如,CDDFuse 将卷积神经网络(CNN)、可逆神经网络(INN)和 Transformer 融合为一种混合结构,需要付出大量努力以实现不同架构之间的有效协同。
为了解决上述问题,我们从模型训练和网络设计两个层面提出了一种综合性框架。具体而言,在模型训练方面,为了在避免任务冲突的同时有效利用跨任务的互补信息,我们开展了一系列实验,分析任务特定学习方法在跨任务推理过程中生成的融合图像的视觉特性。实验结果表明,针对单一任务训练的模型在全局亮度和曝光等方面会产生明显失真,但在局部结构信息上存在互补性。基于实验结果,我们得出两点结论:
i) 不同图像融合任务之间存在冲突,使得单一模型难以在多种图像融合任务上同时取得良好性能;
ii) 不同图像融合任务之间存在信息互补性。
我们进一步通过分析融合图像的梯度图验证了这一观察结果。基于上述发现,我们提出了一种结合序列式梯度迁移的训练框架。在该框架中,我们依次使用 MFIF、MEIF 和 IVF 任务的数据对模型进行训练,其中前一阶段训练得到的模型作为后一阶段的教师模型,其生成的图像梯度被用于下一阶段的训练。通过为每一类任务训练独立模型,我们有效避免了任务目标冲突的问题;同时,跨任务的梯度迁移使模型能够提取不同任务之间的互补结构信息。
在网络设计方面,我们不再依赖经验驱动的设计方式,而是从一种适用于多种图像融合任务的基本融合规则出发,将其展开为一个可学习的迭代算法。进一步地,我们引入深度平衡(DEQ)模型,对该算法进行隐式建模,从而避免显式展开,构建了一种高效且通用的图像融合网络。该方法在保持可比性能的同时,显著减少了模型参数量和训练内存开销。
我们将序列式梯度迁移训练算法与基于基本融合规则的隐式展开网络整合到一个统一框架中。该综合方法不仅提升了多种任务下的融合性能,还提高了计算效率,从而提供了一种更加平衡且实用的解决方案。
我们的主要贡献如下:
• 受不同任务和模型之间普遍存在的互补结构信息启发,我们提出了一种新颖且首次提出的通用图像融合训练范式。与任务特定模型不同,该框架通过序列式梯度迁移机制显式挖掘任务间相关性。
• 基于多种图像融合任务可通过基本融合规则进行统一建模的认识,我们提出了一种源自经典融合公式的统一深度展开网络。
• 为了提升效率,我们将 DEQ 模型引入网络中,构建了一种隐式结构,从而消除了对迭代展开的需求。该改进在保持竞争性性能的同时,显著提高了内存和参数效率。
• 在四种图像融合任务上的大量实验表明,所提出的方法在视觉质量和客观评价指标方面均取得了极具竞争力的性能,同时展现出显著的效率优势。此外,该方法在未见过的数据和任务上表现出良好的泛化能力。消融实验进一步验证了所提出框架中各核心组件的有效性。
2 相关工作
在本节中,我们回顾了与本文研究最为相关的已有工作,从而突出本文工作的创新性。
2.1 图像融合方法
2.1.1 传统图像融合方法
传统的图像融合方法通常在某一变换域中进行图像融合。首先,利用预定义的变换将源图像投影到变换域中;随后,通过简单的人工设计规则(如取最大值规则、加权平均规则)完成融合;最后,通过逆变换得到最终的融合图像。常用的变换包括小波变换、移位特征变换、非下采样轮廓波变换以及目标增强多尺度变换。这类方法依赖人工设计的变换进行特征提取,并采用简单的融合规则,往往难以有效表征复杂特征。
2.1.2 基于深度学习的非通用图像融合方法
基于深度学习的非通用图像融合方法通常针对特定任务进行设计。这类方法大体可分为两类:基于 CNN 的方法和基于 Transformer 的方法。基于 CNN 的方法更擅长提取局部特征,代表性工作包括 LRRNet 等。例如,LRRNet 提出了一种卷积稀疏字典编码网络,用于解决 IVF 问题。基于 Transformer 的方法在捕获全局特征方面更具优势。例如,YDTR 采用 Y 形 Transformer 架构来解决 IVF 任务。近期提出的 EAT 模型引入了一种焦点 Transformer 网络,用于关注显著区域并建立长程多曝光关系,从而通过对抗学习解决 MEIF 问题。此外,ITFuse 作为一种用于 IVF 的交互式 Transformer 框架,通过特征交互模块和重建机制来缓解信息损失。与此同时,基于 GAN 的图像融合方法,通过生成器和判别器学习分布映射。FusionGAN 是首个专门针对 IVF 任务设计的 GAN 方法。
2.1.3 基于深度学习的通用图像融合方法
IFCNN 是首个基于深度学习的通用图像融合模型。该方法通过在模拟的 MFIF 数据集上进行大量数据增强来训练一个鲁棒模型,使其能够泛化到其他图像融合任务。随后,U2Fusion 采用持续学习的方式,同时对多种图像融合任务进行无监督学习。相比之下,SwinFusion、CddFuse、CUNet、PMGI、SDNet、SFINet 以及 DCINN 等方法采用任务特定训练策略,为每个任务分别独立训练模型。近年来,TCMOA 和 PSLPT 利用多任务学习来构建通用图像融合模型。TIMFuse 首先通过多任务学习获得一个预训练模型,然后针对每个具体任务进行微调以提升性能。在这些方法中,U2Fusion 与本文方法最为相似。然而,本文方法与 U2Fusion 存在两个关键差异。首先,我们为每一种图像融合任务训练一个独立模型,而 U2Fusion 对所有任务仅使用一个模型。这种单模型策略容易引发任务冲突问题(导致性能下降),而本文方法有效避免了这一问题。其次,我们在序列式训练过程中引入迁移学习,以提取互补的结构信息,从而更好地保留结构细节。
2.2 迁移学习
迁移学习旨在利用在先前任务或领域中学到的知识来提升新任务或新领域中的学习性能。尽管迁移学习已广泛应用于图像分类、目标检测和图像分割等计算机视觉任务中,但在图像融合领域的研究仍相对较少。在本文中,我们采用迁移学习技术来利用不同图像融合任务之间互补的结构信息。
2.3 深度平衡模型
大多数基础模型(如 ResNet、DenseNet 和 SwinTransformer)由一系列参数不同的基本模块组成,这些模块按顺序执行前向计算以学习映射关系。因此,为了进行前向传播和梯度计算,必须存储每一层的特征图。随着模型深度或宽度的增加,参数数量和计算成本也会相应增加。与此不同,深度平衡(DEQ)模型通过反复使用同一个基本模块来学习非线性映射。由于该迭代过程可视为不动点迭代,当迭代次数趋于无穷时,过程将收敛到平衡点。DEQ 模型通过数值分析方法直接求解该平衡点,从而避免显式的前向计算。因此,DEQ 模型无需存储中间结果,从而降低了训练过程中的内存需求。DEQ 模型已在语义分割、目标检测等多种计算机视觉任务中展现出良好性能。本文基于这样一个认识:深度展开模型可以被视为一种不动点迭代过程,并可通过 DEQ 模型高效求解。在此基础上,我们提出了一种针对融合规则驱动展开模型的全新 DEQ 求解器,以进一步提升效率。
2.4 图像融合的深度展开
大多数基于 DL 的图像融合方法通常依赖经验进行网络结构设计,这一过程不仅耗时,而且可解释性较差。相比之下,深度展开方法通过展开优化算法来构建图像融合网络,从而有效缓解了上述问题。在 MCSC 中,作者首先提出了一种多模态卷积稀疏字典学习模型。LRRNet 针对多模态图像融合问题引入了一种低秩表示学习模型。文献通过展开一个双层优化算法来解决多模态图像融合问题,而 AUIF 则通过展开图像分解算法构建了一种图像融合网络。此外,M2CDL 提出了一种多尺度、多模态的卷积字典学习模型。现有的深度展开方法主要集中于通过展开特定优化算法来构建网络,其应用范围通常局限于多模态图像融合问题。然而,在通用图像融合任务中,深度展开方法的研究仍存在明显不足。不同于上述方法,本文通过展开基本融合规则来构建通用图像融合网络。该方法不仅保留了现有深度展开方法的优势,而且实现了对多种图像融合任务的统一建模。因此,所提出的网络能够适应超越多模态图像融合的更广泛图像融合场景。
3 提出的方法
本文提出了一种综合性的图像融合框架,涵盖网络设计与模型训练两个方面。首先,我们介绍用于模型训练的序列式梯度迁移框架。随后,在网络设计方面,我们阐述基于基本融合规则的深度展开网络。
3.1 序列式梯度迁移框架
我们的方法源于如下观察:针对特定任务训练的模型在同任务测试时往往难以充分保留结构信息;然而,当在不同任务之间进行交叉测试时,这些模型往往会呈现出互补的结构信息。基于这一观察,我们提出序列式梯度迁移框架,以利用跨任务的结构信息,从而增强对源图像结构细节的保留能力。
3.1.1 关键观察
为说明我们的关键观察,我们在 MFIF、MEIF 和 IVF 三个任务上,使用相同的网络结构分别独立训练了三个模型(网络结构细节见第 3.2 节)。在 MFIF 任务中,我们使用 RealMFF 数据集;在 MEIF 任务中,我们使用广泛采用的 SICE 数据集;在 IVF 任务中,我们使用 TNO 数据集。由于 RealMFF 和 SICE 数据集带有标注,我们采用基于 SSIM 指标的损失函数进行有监督训练。对于无标注的 TNO 数据集,我们采用了 SwinFusion 使用的无监督损失函数,该方法表现出较高性能。

同任务测试结果如图 2 第三列所示。对于 MFIF 任务,性能令人满意。然而,在 MEIF 任务中,融合图像缺乏局部细节,可能是由于源图像之间存在显著曝光差异,从欠曝光与过曝光区域引入噪声所致。对于 IVF 任务,生成图像未能保留红外图像中的结构信息,这可能源于显著的模态差异以及源图像本身较低的视觉质量。总体而言,任务特定训练方法难以保留源图像的结构信息。
跨任务测试结果如图 2 第四、第五列所示。对于 MFIF 任务,同任务性能较强,跨任务结果并未呈现互补信息。在 MEIF 任务中,尽管基于 MFIF 数据训练的模型相较同任务结果引入了明显的全局亮度失真,但其呈现出显著的结构信息互补性。类似地,IVF 任务在跨任务测试时也体现出这种互补性。我们将这些现象归因于 MFIF 任务的数据质量高于 IVF 与 MEIF 任务:在高质量数据上训练的模型更倾向于保留结构信息。支持该推断的证据包括在、文献中先在高质量模拟数据上进行预训练,再对 IVF 数据进行微调。通过分析对应图像的梯度图,我们进一步验证了结构信息互补性的存在。

为验证该观察并非孤立现象、且与网络结构无关,我们进一步采用相同的数据集与训练流程训练了两种具有代表性的通用图像融合方法:U2Fusion 与 SwinFusion。训练后的模型在同任务与跨任务设置下进行评估。实验结果如图 3 所示,其中每个任务展示两组样本用于说明。可以观察到,U2Fusion 与 SwinFusion 均表现出跨任务迁移效应,并且该现象在多组样本中一致存在。基于这一观察,我们提出了一种专门用于提取与迁移互补结构信息的学习框架,以提升结构细节的保留能力。
3.1.2 训练框架
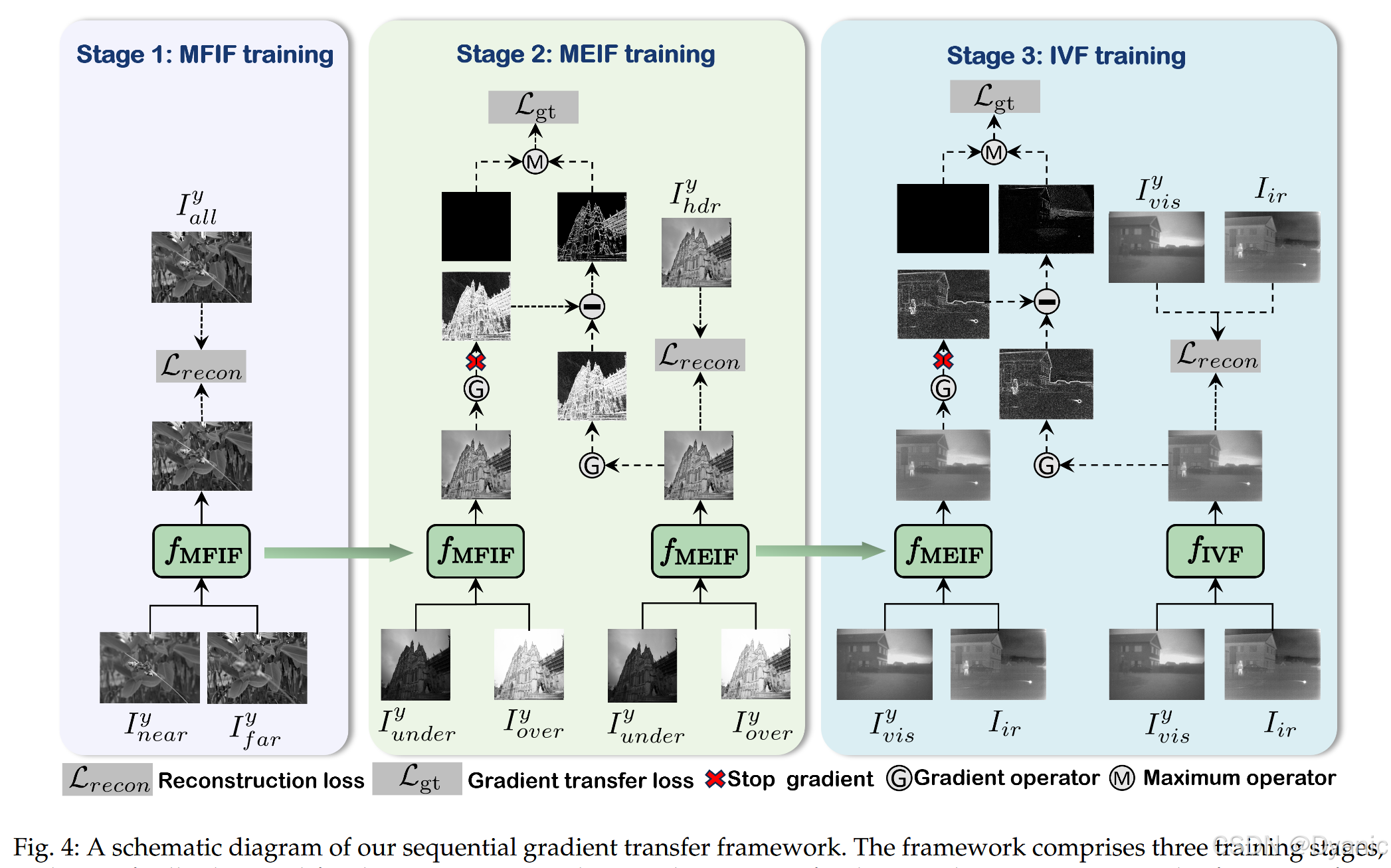
受上述观察启发,并考虑到图像梯度能够有效表征图像的结构信息,我们提出一个三阶段的序列式梯度迁移学习框架(如图 4 所示),以获取跨任务的互补结构信息。在这三个阶段中,我们依次针对 MFIF、MEIF 与 IVF 任务训练三个模型。对于 MFIF 任务,我们将 I near I_{\text{near}} Inear、 I far I_{\text{far}} Ifar 与 I all I_{\text{all}} Iall 分别定义为近焦图、远焦图与全焦图(即参考图像)。对于 MEIF 任务,令 I under I_{\text{under}} Iunder、 I over I_{\text{over}} Iover 与 I hdr I_{\text{hdr}} Ihdr 分别表示欠曝光图、过曝光图与高动态范围图(即参考图像)。对于 IVF 任务,令 I vis I_{\text{vis}} Ivis 与 I ir I_{\text{ir}} Iir 分别表示可见光图像与红外图像。我们的目标是为每个任务在同一网络结构下训练三个模型,即 f MFIF f_{\text{MFIF}} fMFIF、 f MEIF f_{\text{MEIF}} fMEIF 与 f IVF f_{\text{IVF}} fIVF。
鉴于数据集中同时包含 RGB 与灰度图像,我们将所有 RGB 图像转换至 YCrCb 颜色空间,并仅使用 Y 分量进行训练。在得到目标图像的 Y 分量后,我们对源图像的 Cr 与 Cb 分量采用简单的加权平均组合,以得到目标图像的 Cr 与 Cb 分量。各阶段使用的损失函数包含图像重建损失项与梯度迁移损失项:
L = L recon + λ L gt (1) L = L_{\text{recon}} + \lambda L_{\text{gt}} \tag{1} L=Lrecon+λLgt(1)
其中 L recon L_{\text{recon}} Lrecon 表示重建损失, L gt L_{\text{gt}} Lgt 表示梯度迁移损失, λ \lambda λ 为权重系数。为有效训练网络,我们将整个流程划分为三个训练阶段(更多细节见图 4):
• 在第一阶段训练中,考虑到 MFIF 任务能够为 MEIF 与 IVF 任务提供互补结构信息,并且 MFIF 可通过任务特定训练有效解决(如图 2 所示),我们首先聚焦于 MFIF 任务的训练。训练过程优化如下重建损失函数:
L recon s 1 = 1 − SSIM ( f MFIF ( I near y , I far y ) , I all y ) (2) L^{s1}{\text{recon}} = 1-\text{SSIM}\left(f{\text{MFIF}}(I^y_{\text{near}}, I^y_{\text{far}}), I^y_{\text{all}}\right) \tag{2} Lrecons1=1−SSIM(fMFIF(Ineary,Ifary),Ially)(2)
其中 s 1 s1 s1 表示阶段 1,SSIM 为结构相似性指标,变量 I near y I^y_{\text{near}} Ineary、 I far y I^y_{\text{far}} Ifary 与 I all y I^y_{\text{all}} Ially 分别表示近焦、远焦与全焦图像的 Y 分量。在该阶段,由于未应用梯度迁移策略,梯度迁移损失的权重设为 0。
• 在第二阶段训练中,我们继续训练 MEIF 任务模型,并利用 f MFIF f_{\text{MFIF}} fMFIF 中包含的互补结构信息。鉴于图像梯度能有效捕获结构信息,我们利用图像梯度进行互补结构信息迁移,同时避免迁移潜在的负面信息。具体通过优化如下梯度迁移 l 1 l_1 l1 损失实现:
L gt = ∣ ∣ Max ( ∇ f MFIF ( I under y , I over y ) − ∇ f MEIF ( I under y , I over y ) , 0 ) ∣ ∣ 1 (3) L_{\text{gt}} = ||\text{Max}\left(\nabla f_{\text{MFIF}}(I^y_{\text{under}}, I^y_{\text{over}}) - \nabla f_{\text{MEIF}}(I^y_{\text{under}}, I^y_{\text{over}}), 0\right)||_1 \tag{3} Lgt=∣∣Max(∇fMFIF(Iundery,Iovery)−∇fMEIF(Iundery,Iovery),0)∣∣1(3)
其中 ∣ ∣ ⋅ ∣ ∣ 1 ||\cdot||1 ∣∣⋅∣∣1 为 l 1 l_1 l1 范数,Max 为取最大值算子, ∇ \nabla ∇ 为梯度算子, I under y I^y{\text{under}} Iundery 与 I over y I^y_{\text{over}} Iovery 分别对应欠曝光与过曝光图像的 Y 分量。该形式确保仅迁移满足 ∇ f MFIF ( I under y , I over y ) > ∇ f MEIF ( I under y , I over y ) \nabla f_{\text{MFIF}}(I^y_{\text{under}}, I^y_{\text{over}}) > \nabla f_{\text{MEIF}}(I^y_{\text{under}}, I^y_{\text{over}}) ∇fMFIF(Iundery,Iovery)>∇fMEIF(Iundery,Iovery) 的区域,因为更大的梯度意味着更显著的结构信息。此外,我们还继续优化(2)中的重建损失。
• 在第三阶段,我们训练 IVF 任务模型。来自 MEIF 任务的互补信息同样通过梯度迁移用于辅助学习。梯度迁移损失与(3)类似计算。由于缺少标注数据,我们遵循 SwinFusion 的做法,采用如下重建损失:
L recon s 3 = L int + β 1 L text + β 2 L stru (4) L^{s3}{\text{recon}} = L{\text{int}} + \beta_1 L_{\text{text}} + \beta_2 L_{\text{stru}} \tag{4} Lrecons3=Lint+β1Ltext+β2Lstru(4)
其中 L int L_{\text{int}} Lint 表示强度损失, L text L_{\text{text}} Ltext 表示梯度域纹理损失, L stru L_{\text{stru}} Lstru 表示结构损失, β 1 \beta_1 β1 与 β 2 \beta_2 β2 为权重系数。 L int L_{\text{int}} Lint 可计算为:
L int = ∣ ∣ f IVF ( I vis y , I ir ) − Max ( I vis y , I ir ) ∣ ∣ 1 (5) L_{\text{int}} = ||f_{\text{IVF}}(I^y_{\text{vis}}, I_{\text{ir}}) - \text{Max}(I^y_{\text{vis}}, I_{\text{ir}})||_1 \tag{5} Lint=∣∣fIVF(Ivisy,Iir)−Max(Ivisy,Iir)∣∣1(5)
其中 I vis y I^y_{\text{vis}} Ivisy 表示可见光图像的 Y 分量。 L text L_{\text{text}} Ltext 可计算为:
L text = ∣ ∣ ∇ f IVF ( I vis y , I ir ) − Max ( ∇ I vis y , ∇ I ir ) ∣ ∣ 1 (6) L_{\text{text}} = ||\nabla f_{\text{IVF}}(I^y_{\text{vis}}, I_{\text{ir}}) - \text{Max}(\nabla I^y_{\text{vis}}, \nabla I_{\text{ir}})||_1 \tag{6} Ltext=∣∣∇fIVF(Ivisy,Iir)−Max(∇Ivisy,∇Iir)∣∣1(6)
此外, L stru L_{\text{stru}} Lstru 可计算为:
L stru = 1 − SSIM ( f IVF ( I vis y , I ir ) , I vis y ) + 1 − SSIM ( f IVF ( I vis y , I ir ) , I ir ) (7) L_{\text{stru}} = 1-\text{SSIM}\left(f_{\text{IVF}}(I^y_{\text{vis}}, I_{\text{ir}}), I^y_{\text{vis}}\right) + 1-\text{SSIM}\left(f_{\text{IVF}}(I^y_{\text{vis}}, I_{\text{ir}}), I_{\text{ir}}\right) \tag{7} Lstru=1−SSIM(fIVF(Ivisy,Iir),Ivisy)+1−SSIM(fIVF(Ivisy,Iir),Iir)(7)
备注 1(MEIF 任务的颜色问题)
如前所述,在 MEIF 任务训练过程中,源图像被转换到 YCrCb 颜色空间,仅使用 Y 分量进行训练,然后采用简单加权平均方法计算目标 Cr 与 Cb 分量。然而在 MEIF 任务中,由于源图像之间存在显著曝光差异,该方法可能导致严重的颜色失真。为解决该问题,我们设计了 ColorNet(细节见补充材料第 1 节),对第二阶段训练生成的融合图像进行颜色校正。ColorNet 利用融合图像的 Y 分量以及源图像的 Cr 与 Cb 分量来预测准确的 Cr 与 Cb 分量。ColorNet 通过如下 l 1 l_1 l1 损失进行训练:
L color = ∣ ∣ f color ( I under crcb , I over crcb , I ^ hdr y ) − I hdr crcb ∣ ∣ 1 (8) L_{\text{color}} = ||f_{\text{color}}(I^{\text{crcb}}{\text{under}}, I^{\text{crcb}}{\text{over}}, \hat{I}^{y}{\text{hdr}}) - I^{\text{crcb}}{\text{hdr}}||_1 \tag{8} Lcolor=∣∣fcolor(Iundercrcb,Iovercrcb,I^hdry)−Ihdrcrcb∣∣1(8)
其中 f color f_{\text{color}} fcolor 表示 ColorNet, I under crcb I^{\text{crcb}}{\text{under}} Iundercrcb 与 I over crcb I^{\text{crcb}}{\text{over}} Iovercrcb 分别表示欠曝光与过曝光图像对应的 CrCb 分量, I ^ hdr y = f MEIF ( I under y , I over y ) \hat{I}^{y}{\text{hdr}} = f{\text{MEIF}}(I^y_{\text{under}}, I^y_{\text{over}}) I^hdry=fMEIF(Iundery,Iovery) 表示融合得到的 Y 分量, I hdr crcb I^{\text{crcb}}_{\text{hdr}} Ihdrcrcb 为参考 CrCb 分量。
3.2 网络设计
在介绍完序列式梯度迁移训练算法后,我们将详细描述在该训练算法下训练的通用图像融合网络。我们的目标是基于一个基本融合原则构建通用图像融合网络。我们首先给出该规则的一般形式;然后对其展开以形成可学习的图像融合算法;接着将该算法与 DEQ 模型结合以提出更高效的解决方案;最后对这些算法进行参数化,得到两种通用图像融合网络 FRUFN 与 EFRUFN。
3.2.1 融合规则展开网络(FRUFN)
(I)数学推导
对于包括 MFIF、MEIF、IVF 与 MMF 在内的广泛图像融合任务,存在一个能够促进统一建模的基本融合原则。令矩阵 I 1 I_1 I1 与 I 2 I_2 I2 表示单波段源图像, I ^ \hat{I} I^ 表示融合结果。基本图像融合规则可一般表述为:
I ^ = T − 1 ( M ⊙ T 1 ( I 1 ) + ( 1 − M ) ⊙ T 2 ( I 2 ) ) (9) \hat{I} = T^{-1}\left(M \odot T_1(I_1) + (1-M)\odot T_2(I_2)\right) \tag{9} I^=T−1(M⊙T1(I1)+(1−M)⊙T2(I2))(9)
其中 T 1 ( ⋅ ) T_1(\cdot) T1(⋅) 与 T 2 ( ⋅ ) T_2(\cdot) T2(⋅) 为变换,用于将单波段源图像投影到高维空间, T − 1 T^{-1} T−1 为逆变换, ⊙ \odot ⊙ 表示逐元素乘法, M M M 为与融合规则对应的掩码。在变换后的高维空间中,有:
F = M ⊙ F 1 + ( 1 − M ) ⊙ F 2 (10) F = M \odot F_1 + (1-M)\odot F_2 \tag{10} F=M⊙F1+(1−M)⊙F2(10)
其中 F 1 = T 1 ( I 1 ) F_1=T_1(I_1) F1=T1(I1)、 F 2 = T 2 ( I 2 ) F_2=T_2(I_2) F2=T2(I2) 为变换后的源图像,并且 I ^ = T − 1 ( F ) \hat{I}=T^{-1}(F) I^=T−1(F)。我们将(10)展开为迭代过程:
F ( n + 1 ) = M ( n ) ⊙ F 1 + ( 1 − M ) ⊙ F ( n ) (11) F^{(n+1)} = M^{(n)} \odot F_1 + (1-M)\odot F^{(n)} \tag{11} F(n+1)=M(n)⊙F1+(1−M)⊙F(n)(11)
其中 n ∈ N + n\in\mathbb{N}^+ n∈N+ 为第 n n n 次迭代,初始化为 F ( 1 ) = F 2 F^{(1)}=F_2 F(1)=F2。相较于(10),该形式允许在不同迭代中使用不同融合规则,从而更具灵活性。值得注意的是,许多主流神经网络由一系列相同的基本单元与残差连接构成。我们的目标是基于(11)设计通用图像融合网络。受这些网络结构启发,我们将(11)改写为残差形式:
F ( n + 1 ) = F ( n ) + M ( n + 1 ) ⊙ ( F 1 − F ( n ) ) (12) F^{(n+1)} = F^{(n)} + M^{(n+1)} \odot (F_1 - F^{(n)}) \tag{12} F(n+1)=F(n)+M(n+1)⊙(F1−F(n))(12)
然而在(12)中, F ( n ) F^{(n)} F(n) 与 F 1 F_1 F1 仅通过 M ( n + 1 ) M^{(n+1)} M(n+1) 间接交互,效率不足。为此,我们引入额外变换 T ( n ) T^{(n)} T(n) 以增强交互能力:
F ( n + 1 ) = F ( n ) + M ( n + 1 ) ⊙ T ( n ) ( F 1 − F ( n ) ) (13) F^{(n+1)} = F^{(n)} + M^{(n+1)} \odot T^{(n)}(F_1 - F^{(n)}) \tag{13} F(n+1)=F(n)+M(n+1)⊙T(n)(F1−F(n))(13)
随后,我们对固定掩码 M ( n + 1 ) M^{(n+1)} M(n+1) 与变换 T ( n ) T^{(n)} T(n) 进行参数化,得到可学习算法:
F ( n + 1 ) = F ( n ) + G ϕ ( n ) ( F 1 − F ( n ) , M ( n ) ) ⊙ T θ ( n ) ( F 1 − F ( n ) ) (14) F^{(n+1)} = F^{(n)} + G_{\phi^{(n)}}(F_1 - F^{(n)}, M^{(n)}) \odot T_{\theta^{(n)}}(F_1 - F^{(n)}) \tag{14} F(n+1)=F(n)+Gϕ(n)(F1−F(n),M(n))⊙Tθ(n)(F1−F(n))(14)
其中 T θ ( n ) T_{\theta^{(n)}} Tθ(n) 为可学习变换, θ ( n ) \theta^{(n)} θ(n) 为其参数; G ϕ ( n ) G_{\phi^{(n)}} Gϕ(n) 为掩码生成器, ϕ ( n ) \phi^{(n)} ϕ(n) 为其参数,并且 M ( n + 1 ) = G ϕ ( n ) ( F 1 − F ( n ) , M ( n ) ) M^{(n+1)} = G_{\phi^{(n)}}(F_1 - F^{(n)}, M^{(n)}) M(n+1)=Gϕ(n)(F1−F(n),M(n))。 G ϕ ( n ) G_{\phi^{(n)}} Gϕ(n) 不仅利用残差 F 1 − F ( n ) F_1-F^{(n)} F1−F(n),还利用上一迭代学习到的掩码 M ( n ) M^{(n)} M(n) 来预测当前迭代的掩码。此外,我们还将初始变换 T 1 T_1 T1 与 T 2 T_2 T2 参数化为可学习变换 T θ 1 T_{\theta_1} Tθ1 与 T θ 2 T_{\theta_2} Tθ2。当迭代达到预设最大次数 N N N 后,通过可学习逆变换 T θ 3 − 1 T^{-1}_{\theta_3} Tθ3−1 得到融合结果:
I ^ = T θ 3 − 1 ( F ( N ) ) (15) \hat{I} = T^{-1}_{\theta_3}(F^{(N)}) \tag{15} I^=Tθ3−1(F(N))(15)
所提出的算法结合了深度学习模型与传统基于变换方法的优势,算法总结见算法 1(见补充材料)。它允许使用 ResNet、视觉 Transformer 等先进网络对变换与掩码生成器进行参数化;同时通过可学习掩码适配不同融合规则,提高了融合过程的灵活性。
(II)基于推导的网络架构设计
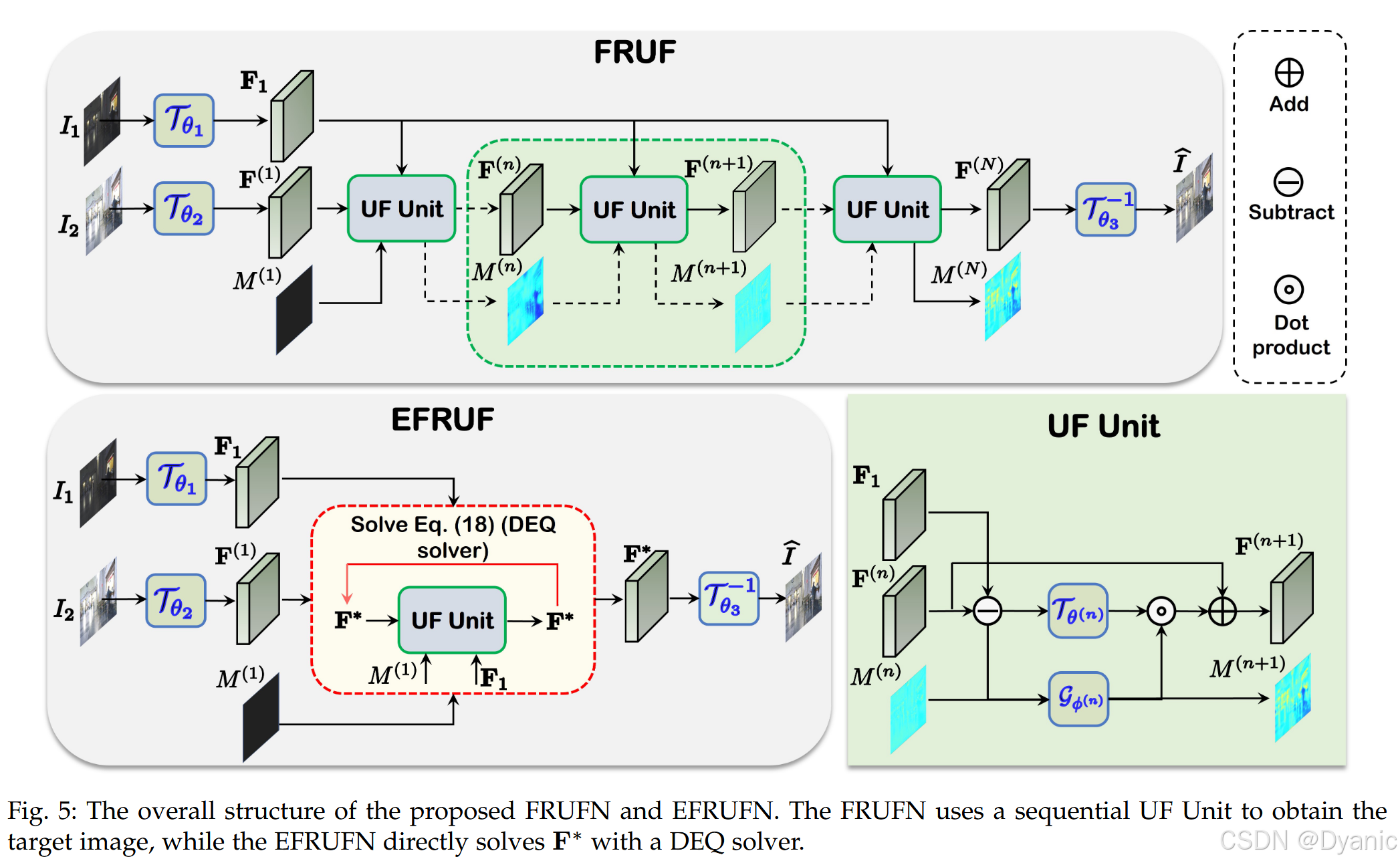
本节基于第 3.2.1(I)的推导分析,提出对应的深度学习网络结构------融合规则展开网络(FRUFN)。如图 5 所示,FRUFN 接收源图像 I 1 I_1 I1 与初始掩码 M ( 1 ) M^{(1)} M(1),以迭代方式细化变换后的源图像 I 2 I_2 I2,并预测新的掩码。我们将 M ( 1 ) M^{(1)} M(1) 初始化为零矩阵。FRUFN 包含三个主要组件:i)初始变换 T θ 1 T_{\theta_1} Tθ1 与 T θ 2 T_{\theta_2} Tθ2,将源图像投影到特征空间;ii)展开单元(UF Unit),通过从 I ∗ 1 I*1 I∗1 中提取互补信息迭代细化融合结果;iii)逆变换 T θ 3 − 1 T^{-1}{\theta_3} Tθ3−1,将特征重建为最终融合图像。我们经验性地将 T θ 1 T_{\theta_1} Tθ1 与 T θ 2 T_{\theta_2} Tθ2 设计为一层卷积与两个残差块(如图 6 所示)。UF Unit 通过对(14)中的 T θ ( n ) T_{\theta^{(n)}} Tθ(n) 与 G ϕ ( n ) G_{\phi^{(n)}} Gϕ(n) 参数化进行构建。对于目标是从两幅源图像中提取丰富互补信息的 T θ ( n ) T_{\theta^{(n)}} Tθ(n),我们采用基于 CNN-Transformer 混合结构的全局-局部变换(GLT)进行建模。动态可学习掩码 G ϕ ( n ) G_{\phi^{(n)}} Gϕ(n) 负责学习语义注意权重,以促进两幅源图像间的特征交互,我们使用多尺度掩码生成器(MSMG)对其建模。
全局-局部变换(GLT)
由于 T θ ( n ) T_{\theta^{(n)}} Tθ(n) 用于学习源图像的互补特征,这些特征既包含局部特征(例如可见光图像中的高频细节),也包含全局特征(例如红外图像中的显著目标),因此我们提出 GLT(见图 6 下半部分)来建模 T θ ( n ) T_{\theta^{(n)}} Tθ(n)。GLT 采用 CNN-Transformer 混合结构,其中 CNN 负责学习局部特征,Transformer 负责学习全局特征。具体而言,我们使用两层卷积学习局部特征,并使用 Swin-Transformer block(SwinBlock)学习长程特征,因为其能够处理不同分辨率图像,并由于移位窗口机制而具有较高的内存效率。鉴于 SwinBlock 训练时可能存在收敛不稳定问题,我们在卷积层与 SwinBlock 之间插入两层归一化以稳定训练。
多尺度掩码生成器(MSMG)
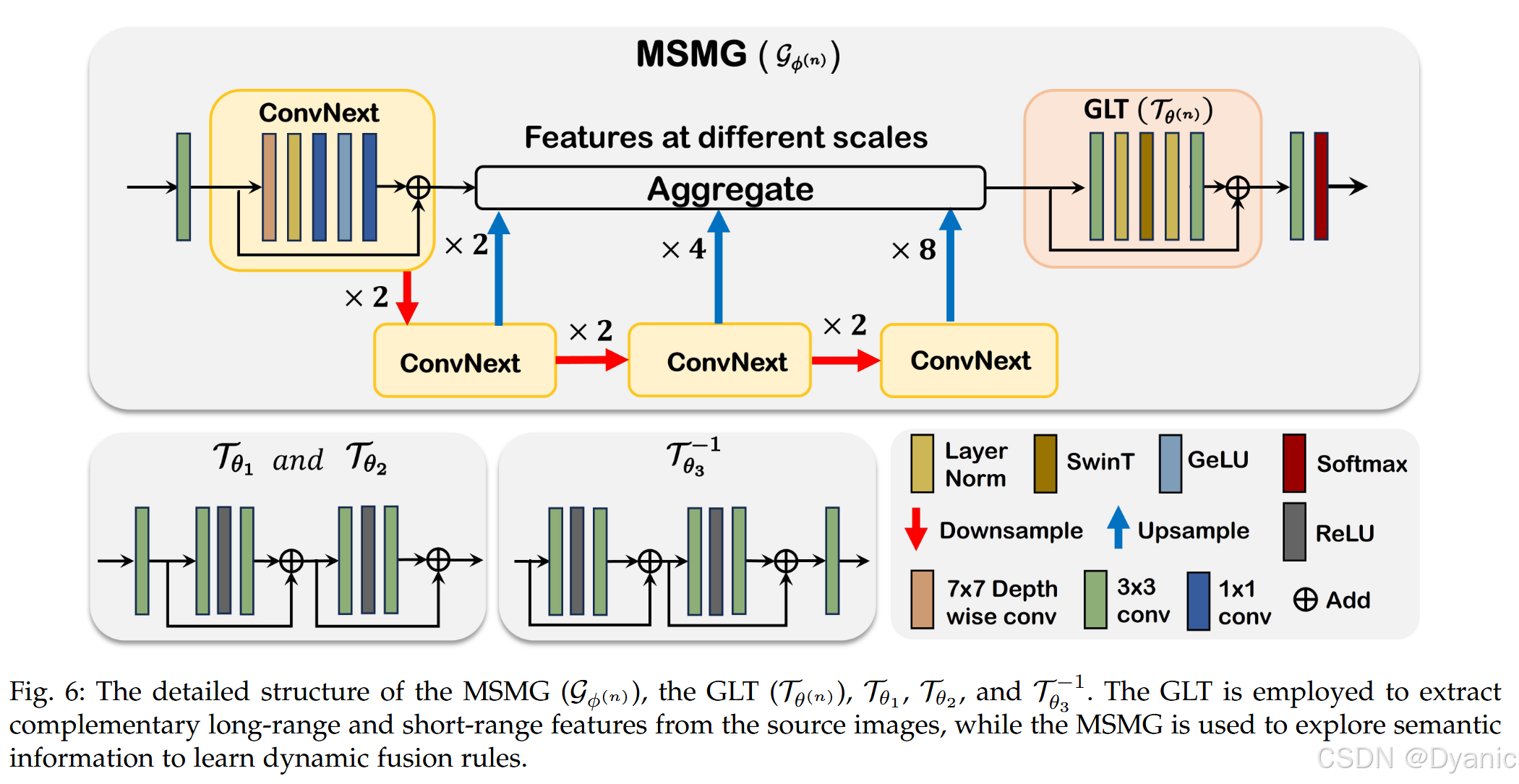
为建模自适应可学习掩码,神经网络需要能够挖掘语义信息,因此必须具备较大的感受野。受语义分割任务相关架构启发,我们将掩码生成器设计为多尺度结构(见图 6)。具体而言,特征首先经过一层卷积,然后通过最大池化以 2、4、8 倍下采样生成多尺度特征。在每个尺度上,我们使用 ConvNext Block 来丰富多尺度特征。随后,将多尺度特征进行聚合,并进一步送入 GLT 模块以提取更多语义信息。最后,将提取的语义信息投影到两通道特征图,并在通道维度上通过 SoftMax 归一化得到语义图。由此,语义图能够自动区分两幅源图像的信息,并灵活地为其分配合适权重。
3.2.2 高效融合规则展开网络(EFRUFN)
(I)数学推导
由于所提出的算法 1 在每次迭代中使用不同参数,随着迭代次数增加,不仅参数量会增大,内存使用与计算复杂度也会增加。为解决该问题,我们基于(14)提出一种跨迭代参数共享的高效策略,从而显著降低所需参数量:
F ( n + 1 ) = F ( n ) + G ϕ ( F 1 − F ( n ) , M ( n ) ) ⊙ T θ ( F 1 − F ( n ) ) (16) F^{(n+1)} = F^{(n)} + G_{\phi}(F_1 - F^{(n)}, M^{(n)}) \odot T_{\theta}(F_1 - F^{(n)}) \tag{16} F(n+1)=F(n)+Gϕ(F1−F(n),M(n))⊙Tθ(F1−F(n))(16)
其中可学习参数 ϕ \phi ϕ 与 θ \theta θ 在所有迭代中共享。尽管该权重共享策略更加参数高效,但仍保留了原算法的内存与计算需求。将权重共享算法视为不动点过程后,我们可利用 DEQ 来求解。具体地,将(16)右侧视作关于 F ( n ) F^{(n)} F(n) 的统一变量,可重写为:
F ( n + 1 ) = H θ , ϕ ( F ( n ) ) (17) F^{(n+1)} = H_{\theta,\phi}(F^{(n)}) \tag{17} F(n+1)=Hθ,ϕ(F(n))(17)
其中 H θ , ϕ ( F ( n ) ) = F ( n ) + M ( n + 1 ) ⊙ T θ ( F 1 − F ( n ) ) H_{\theta,\phi}(F^{(n)}) = F^{(n)} + M^{(n+1)} \odot T_{\theta}(F_1 - F^{(n)}) Hθ,ϕ(F(n))=F(n)+M(n+1)⊙Tθ(F1−F(n)),并且 M ( n + 1 ) = G ϕ ( F 1 − F ( n ) , M ( n ) ) M^{(n+1)} = G_{\phi}(F_1 - F^{(n)}, M^{(n)}) M(n+1)=Gϕ(F1−F(n),M(n))。若迭代过程收敛,则继续更新不会改变 F ( n + 1 ) F^{(n+1)} F(n+1)。令 F ∗ F^* F∗ 表示平衡点(或收敛点),不动点迭代可表示为:
F ∗ = H θ , ϕ ( F ∗ ) (18) F^* = H_{\theta,\phi}(F^*) \tag{18} F∗=Hθ,ϕ(F∗)(18)
该方程可由 DEQ 高效求解。我们在补充材料的算法 2 中总结了最终的高效算法。具体而言,DEQ 算法主要包含前向与反向过程。在前向过程中,DEQ 可采用加速算法(如 Broyden 方法或 Anderson mixing)来求解不动点问题;同时 DEQ 不存储所有中间结果,从而显著降低计算复杂度与内存消耗。理论上,高效算法的训练内存保持常数,而原算法的训练内存随迭代次数线性增长。
在反向过程中,由于 DEQ 在前向传播中不存储所有特征图,无法直接用链式法则计算参数梯度,而是通过隐式求导间接计算梯度。例如,对于(18)所示不动点表示,对应损失 L L L 关于 θ \theta θ 的梯度为:
∂ L ∂ θ = ∂ L ∂ F ∗ ( E − ∂ L ∂ F ∗ ) − 1 ∂ H θ , ϕ ( F ∗ ) ∂ θ (19) \frac{\partial L}{\partial \theta} = \frac{\partial L}{\partial F^*} \left(E-\frac{\partial L}{\partial F^*}\right)^{-1} \frac{\partial H_{\theta,\phi}(F^*)}{\partial \theta} \tag{19} ∂θ∂L=∂F∗∂L(E−∂F∗∂L)−1∂θ∂Hθ,ϕ(F∗)(19)
其中 E E E 为单位矩阵。由该式可知,我们只需要最终输出 F ∗ F^* F∗,无需获取全部中间结果即可计算梯度。然而,(19)中的 ( E − ∂ L ∂ F ∗ ) − 1 \left(E-\frac{\partial L}{\partial F^*}\right)^{-1} (E−∂F∗∂L)−1 仍难以计算,因为对高维矩阵求逆并不容易,在实现中只能近似计算。文献提出用 E ≈ ( E − ∂ L ∂ F ∗ ) − 1 E \approx \left(E-\frac{\partial L}{\partial F^*}\right)^{-1} E≈(E−∂F∗∂L)−1 来近似该项,并在实验上验证该策略不会损害性能。于是,梯度可近似为:
∂ L ∂ θ ≈ ∂ L ∂ F ∗ ∂ H θ , ϕ ( F ∗ ) ∂ θ (20) \frac{\partial L}{\partial \theta} \approx \frac{\partial L}{\partial F^*} \frac{\partial H_{\theta,\phi}(F^*)}{\partial \theta} \tag{20} ∂θ∂L≈∂F∗∂L∂θ∂Hθ,ϕ(F∗)(20)
(II)基于推导的网络架构设计
基于(18),我们提出 FRUFN 的高效版本,命名为 EFRUFN。图 5(b) 展示了所提出 EFRUFN 的整体流程。EFRUFN 与 FRUFN 在 T θ 1 T_{\theta_1} Tθ1、 T θ 2 T_{\theta_2} Tθ2 与 T θ 3 − 1 T^{-1}{\theta_3} Tθ3−1 等部分相似,我们同样使用 UF Unit 来建模 H θ , ϕ ( F ∗ ∗ ) H{\theta,\phi}(F^**) Hθ,ϕ(F∗∗)。不同于 FRUFN 通过顺序迭代 UF Unit 得到变换域融合结果,EFRUFN 通过求根方法直接计算 F ∗ F^* F∗。因此,EFRUFN 相较 FRUFN 在参数效率与内存效率方面更优。
4 实验
本节致力于描述实验设置与实验结果。我们将首先聚焦于 MFIF、MEIF 和 IVF 任务。随后,我们将通过在 MIF 任务上测试来突出模型的泛化能力。此外,我们将通过若干消融实验验证所提出设计的效率。最后,我们将给出一些讨论,包括参数数量与训练内存需求等关键方面。
4.1 实验设置
4.1.1 网络配置
在网络配置方面,FRUFN 与 EFRUFN 中 SwinBlock、ConvNext block 以及 ResBlock 的特征图通道数均设置为 32。GLT 与 MSMG 中 SwinBlock 的深度与头数分别设置为 2 和 6。GLT 与 MSMG 中 SwinBlock 的窗口大小分别设置为 2 和 4,其中 MSMG 采用更大的窗口大小以扩大感受野。FRUFN 的迭代次数设置为 5。对于 EFRUFN,最大迭代次数同样设置为 5(更多实现细节请参见补充材料第 2 节)。
4.1.2 数据集信息
对于 MFIF 任务,我们使用 RealMFF 与 MFIWHU 数据集。RealMFF 由真实世界样本组成,我们选择其中 700 个样本用于训练(数据集配置见补充材料表 1)。WHU-MFI 为模拟数据集,我们选择其中 96 个样本用于训练。MEIF 任务训练使用 SICE 数据集。SICE 为模拟数据集,我们选择 201 对样本用于训练,其余样本对用于测试。由于每对样本包含多组欠曝光与过曝光图像,我们从每对样本中随机选择一组欠曝光与过曝光图像用于训练。IVF 任务训练方面,我们从 RoadScene(RS)数据集中选取 190 个样本,并从 TNO 数据集中选取 30 个样本用于训练。
4.1.3 评价指标
对于 MFIF、IVF 与 MIF 任务,由于测试集缺少参考(真值)数据,我们使用 EN、MI、SCD 和 MS-SSIM 进行定量评估。此外,除了这些基于浅层特征或信息论的指标,我们还引入了基于深度学习的指标 UNIQUE。与前述指标不同,该指标更强调感知质量。对于带参考图像的 MEIF 任务,我们使用 PSNR、MEF-SSIM 与 MS-SSIM 来评估融合图像与参考图像之间的保真度。相关指标的代码由文献提供。
4.2 MFIF 实验
在 MFIF 实验中,我们使用 Lytro 数据集。原始 Lytro 数据集包含 38 对图像,我们去除视觉质量较差与未配准的图像对,并使用剩余 22 对图像进行测试。我们将所提出方法与非通用图像融合方法进行比较,包括 GFDF、CNNFuse、SESF、ZMFF;同时与通用图像融合方法进行比较,包括 SwinFusion、U2Fusion、IFCNN、TCMOA 和 GIFNet。
4.2.1 视觉结果

图 7 展示了在 Lytro 数据集上的融合结果。评估 MFIF 算法性能的一个重要标准是:在决策边界附近(远焦区域与近焦区域之间的边界)是否能产生较小的失真。为便于分析,我们同时给出局部放大图。从图中可以看出,GFDF、CNNFuse 和 U2Fusion 在决策边界附近丢失了远焦细节。SESF 与 IFCNN 生成的决策边界不准确,而我们的方法能够生成准确的决策边界,并同时保留远焦与近焦细节。TCMOA 与 GIFNet 的融合结果不仅决策边界不清晰,而且在近焦区域存在明显模糊。
4.2.2 定量结果
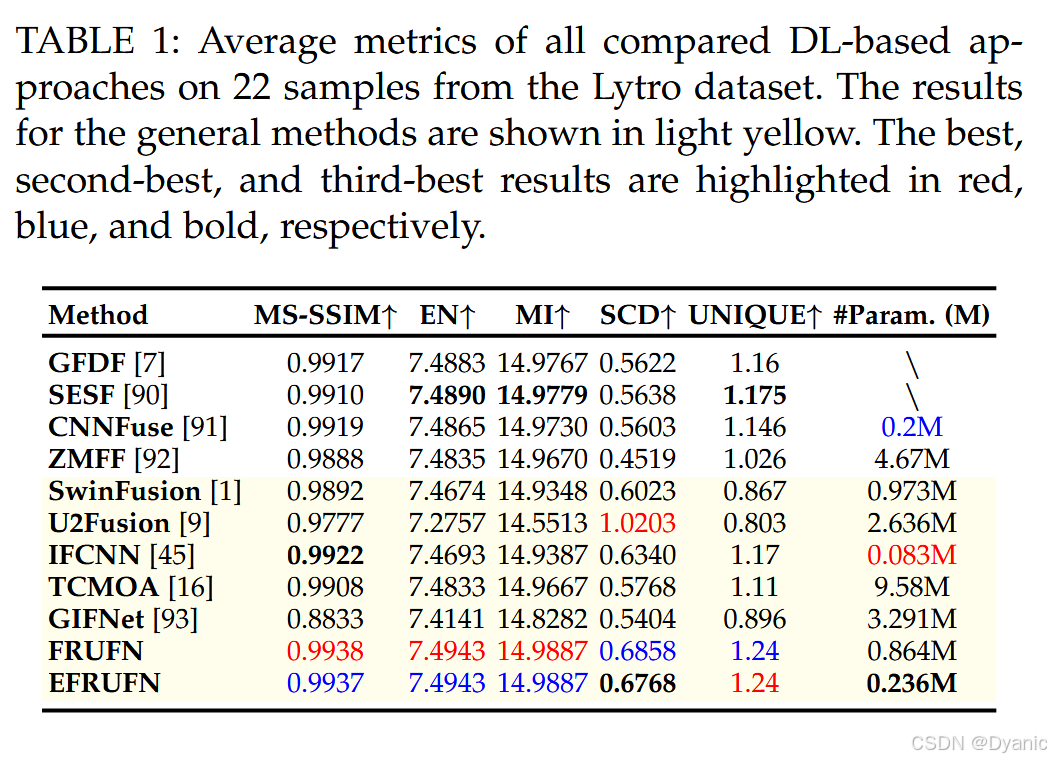
表 1 给出了定量评估结果。以 MS-SSIM、EN、MI 与 UNIQUE 作为质量指标时,我们的方法优于其他对比方法。尽管 U2Fusion 在 SCD 指标上取得最佳结果,但在其余三项指标上表现较差。结合视觉对比实验可知,U2Fusion 的融合结果过度模糊。总体而言,在未显著增加参数量的前提下,我们的方法在所用质量指标上表现出明显优势。此外,EFRUFN 仅用约四分之一的参数量即可取得与 FRUFN 几乎一致的定量结果。
4.3 MEIF 实验
在 MEIF 实验中,我们使用 SICE 数据集。为便于资源管理并保证一致性,我们在测试前将高分辨率原图缩放至 512 × 512 512 \times 512 512×512。我们将所提出方法与多种通用方法比较,包括 IFCNN、U2Fusion 和 SwinFusion;同时与多种非通用方法比较,包括 BHFMEF、DPEMEF、IID、TransMEF、TCMOA 和 GIFNet。
4.3.1 视觉结果

图 8 展示了各方法的融合结果。从红色箭头指示区域可观察到,对比方法未能有效保留背景天空区域的结构细节。此外,IID、TransMEF、SwinFusion 与 U2Fusion 生成的图像存在欠曝光,而 IFCNN 的融合图像则显得过曝光。TCMOA 的结果出现结构畸变,而 GIFNet 的融合结果明显欠曝光。相比之下,我们的方法能够更好地保留源图像的结构信息,并生成曝光更合适的图像。
4.3.2 定量结果
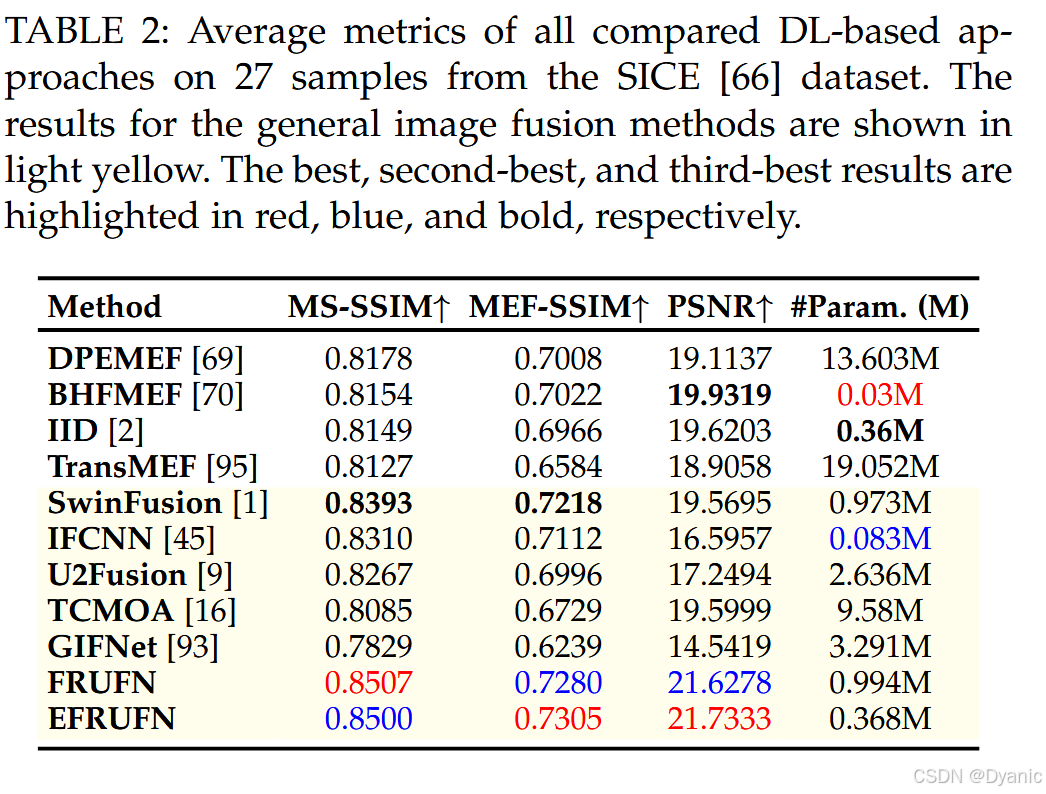
从表 2 可见,FRUFN 与 EFRUFN 在所有指标上均显著优于其他对比方法。FRUFN 与 EFRUFN 的性能相近。在模型参数量方面,大多数方法的参数规模处于同一数量级。
4.4 IVF 实验
在 IVF 实验中,我们使用 RS 与 TNO 数据集。我们将方法与通用与非通用图像融合方法均进行比较。非通用方法包括 RecoNet、LRRNet、EMMA 与 MMIF-INet。通用方法包括 SwinFusion、CDDFuse、U2Fusion、IFCNN、TIMFuse、TCMOA、LFDT 以及 GIFNet。
4.4.1 视觉结果

TNO 数据集上的视觉结果如图 9 所示,而 RS 数据集的对应结果见补充材料图 2。如图 9 所示,从绿色矩形框的局部放大图可以看到,ReCoNet、LRRNet 与 TIMFuse 丢失了红外图像的结构信息。从红色矩形框的局部放大图可见,ReCoNet、SwinFusion、CDDFuse、EMMA 与 TIMFuse 丢失了红外图像的结构信息。蓝色矩形框的局部放大图表明,IFCNN、SwinFusion 与 CDDFuse 的融合结果过于模糊。TCMOA 的结果在背景区域细节呈现不足,而 GIFNet 的结果在显著前景结构上亮度过低。此外,U2Fusion 的结果整体亮度偏低。总体而言,我们的方法能够更好地保留源图像的结构信息。
4.4.2 定量结果
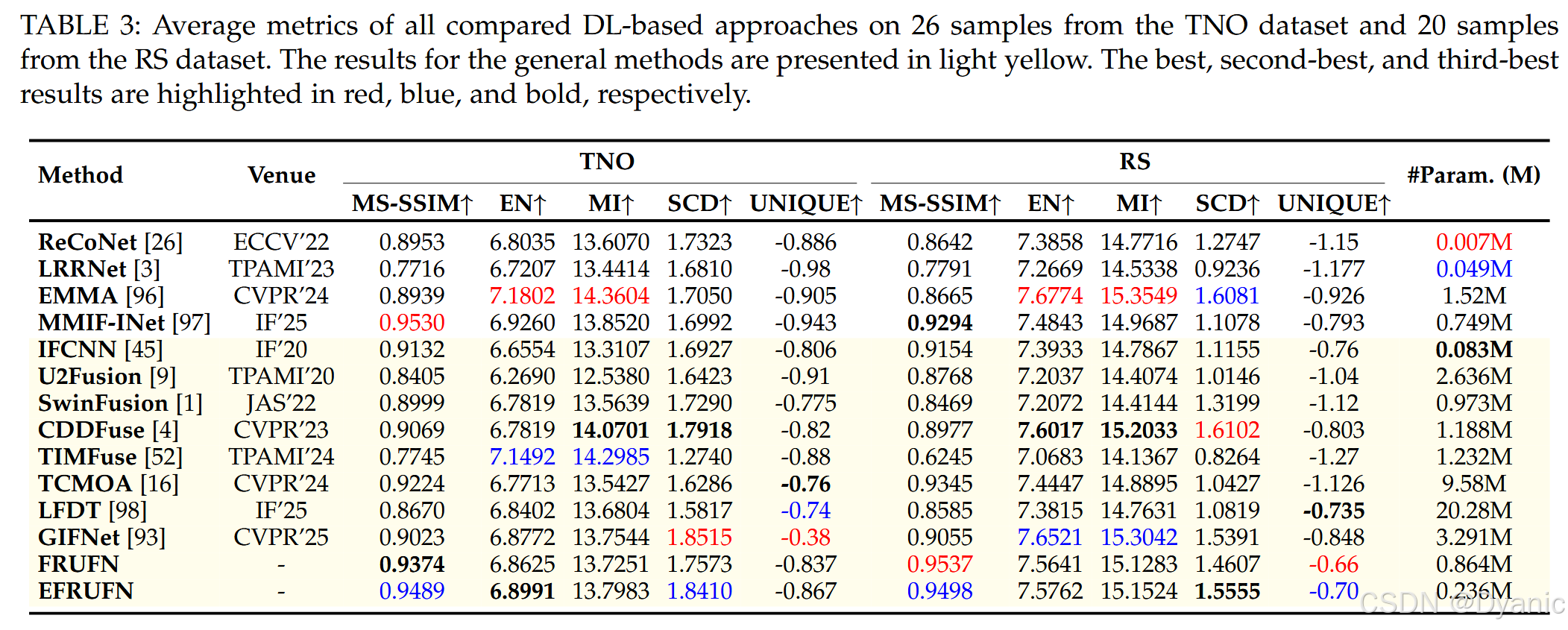
表 3 给出了定量评估结果。相较其他通用图像融合方法,我们的方法在大多数指标上具有竞争力,但在某些情况下略逊于非通用方法 EMMA。然而,与 EMMA 相比,我们的方法具有两点显著优势:第一,EFRUFN 的参数量显著更少;第二,FRUFN 与 EFRUFN 在 MS-SSIM 指标上优于 EMMA,表明其在结构信息保留方面更具优势。
4.5 泛化实验
本节中,我们直接将第二阶段训练得到的模型应用于 MIF 任务,以测试模型的泛化能力。我们选取两类研究较多的 MIF 任务:MRI-CT 图像融合与 MRI-SPECT 图像融合。测试图像来自 Harvard Medical Image 数据集。具体而言,我们随机选择 20 对图像用于 MRI-CT 任务测试,另选 20 对用于 MRI-SPECT 任务测试。我们将所提出方法与非通用方法对比,包括 GeSeNet、FusionMamba、MMIFINet;并与通用方法对比,包括 SwinFusion、CDDFuse、U2Fusion、IFCNN、TIMFuse、LFDT 与 GIFNet。
4.5.1 视觉结果
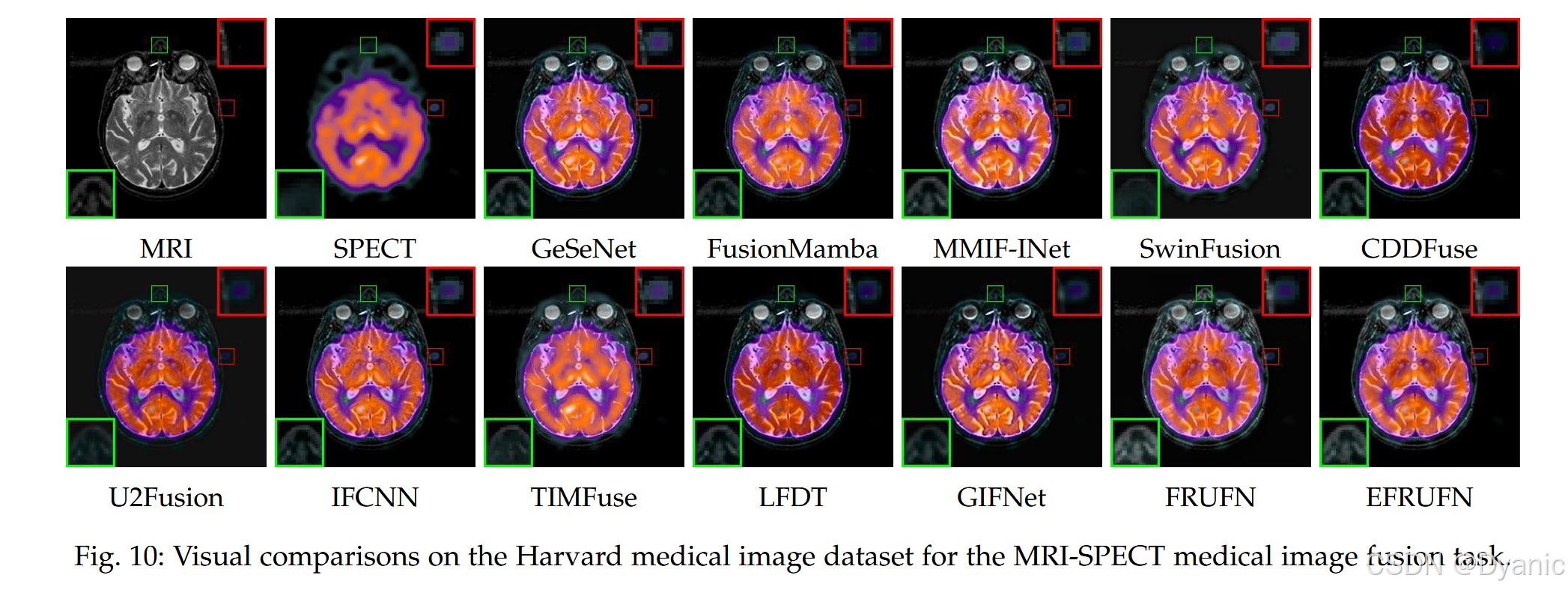
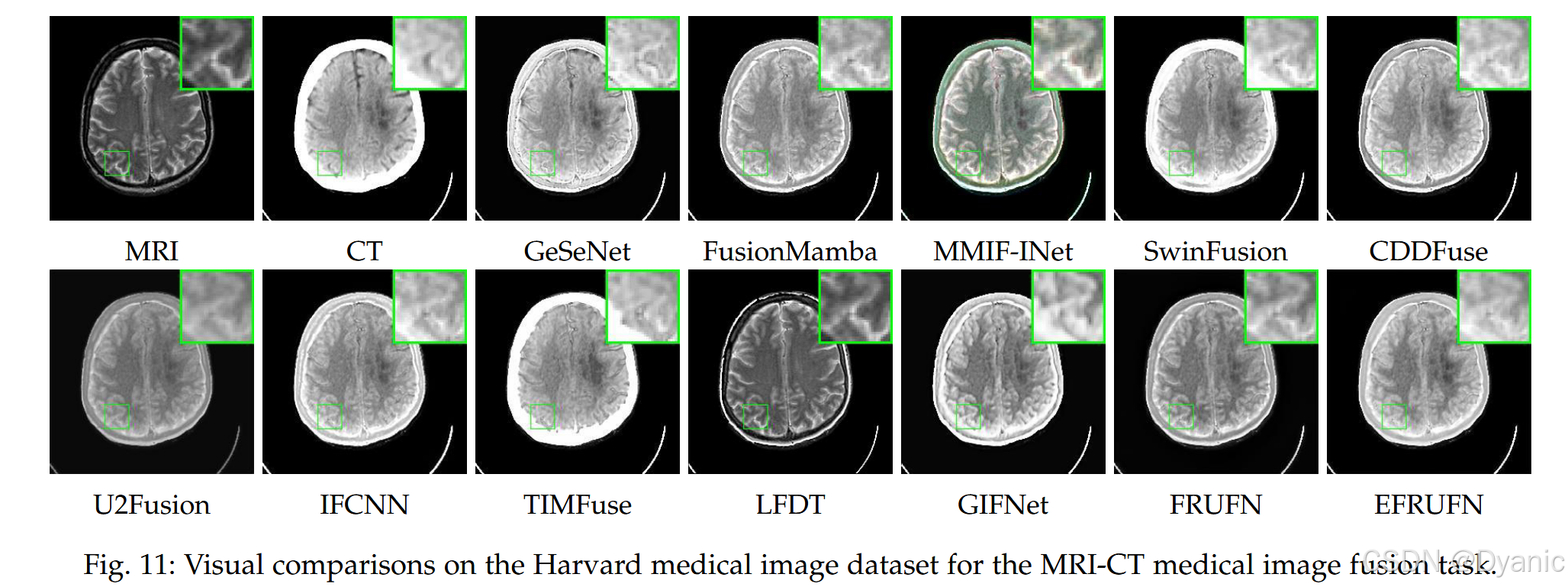
MRI-SPECT 图像融合任务的视觉结果如图 10 所示。从绿色矩形框的局部放大图可见,SwinFusion 丢失了 MRI 图像的结构信息,且 U2Fusion 与 TIMFuse 的结果在结构细节上显得过度模糊。从红色矩形框的局部放大图可见,MATR 与 CDDFuse 丢失了 SPECT 图像的结构信息。GIFNet 与 FusionMamba 的结果丢失了原始 MRI 图像中的细粒度细节信息。总体而言,我们的方法生成的融合图像能够同时保留 MRI 与 SPECT 图像的结构信息。图 11 展示了 MRI-CT 图像融合任务的融合结果。从矩形框局部放大图可见,FRUFN 与 EFRUFN 的结果相比其他方法具有更锐利的边缘与更高的对比度。值得注意的是,我们的模型并未在 MIF 数据上训练,但仍能生成高质量融合图像,这表明我们的方法具有很强的泛化能力,能够在未见过的 MIF 数据上同样表现良好。
4.5.2 定量结果
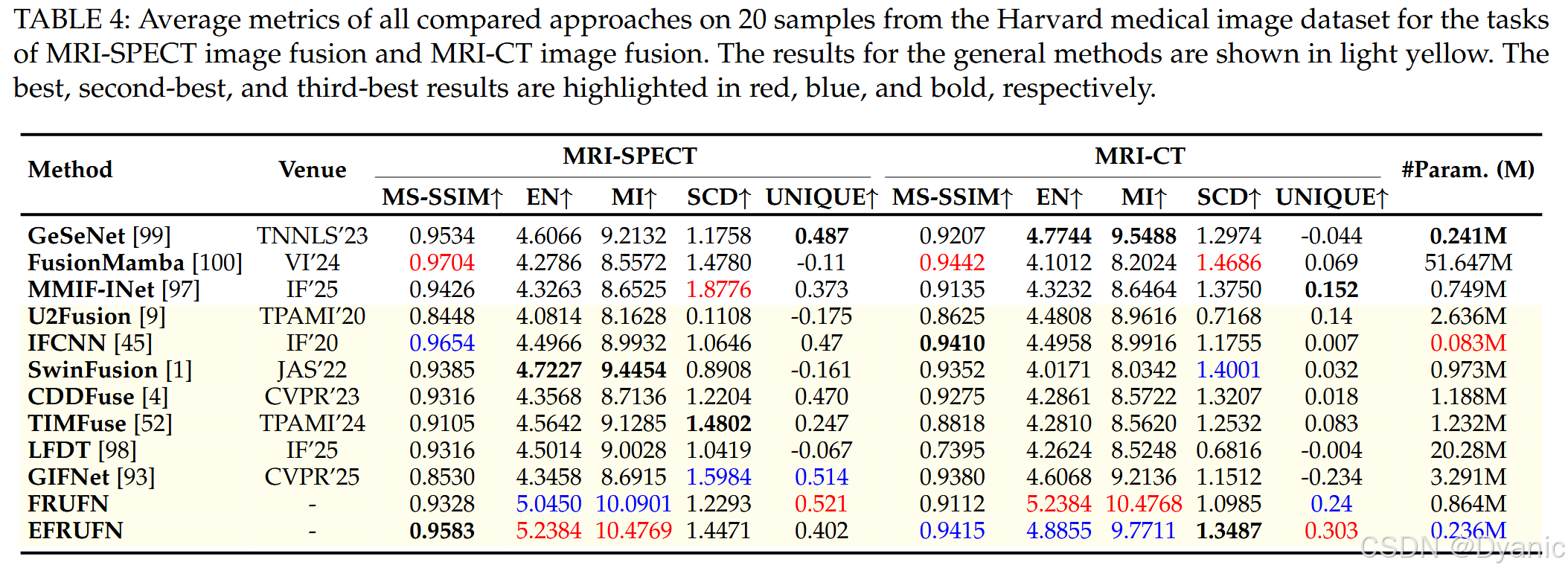
表 4 给出了定量评估结果,显示 FRUFN 在几乎所有情况下都明显优于其他对比方法。EFRUFN 在多项质量指标上也表现强劲。值得注意的是,尽管 FusionMamba 的 MS-SSIM 得分优于我们的方法,但其参数量显著更大。出色的定量结果清晰地凸显了我们方法优秀的泛化能力。
4.6 计算复杂度与运行时间比较

本节比较通用图像融合方法的计算复杂度。表 5 汇总了各方法的 FLOPs、MACs 与运行时间。需要注意的是,U2Fusion 使用较旧版本的 TensorFlow 实现,而其他方法均基于 PyTorch 开发。因此,直接在计算复杂度与运行时间上将 U2Fusion 与其他方法对比在方法论上并不一致。基于此,我们在对比分析中排除了 U2Fusion 的复杂度与运行时间统计。表中结果表明,我们的方法相比 IFCNN 具有更高计算复杂度与更长运行时间,但优于 TCMOA,并与其他方法保持竞争力。此外,EFRUFN 相较 FRUFN 的 FLOPs、MACs 与运行时间略有增加,这归因于其数值算法在推理过程中需要存储中间结果,从而带来一定的计算开销。
4.7 消融实验:序列式梯度迁移框架
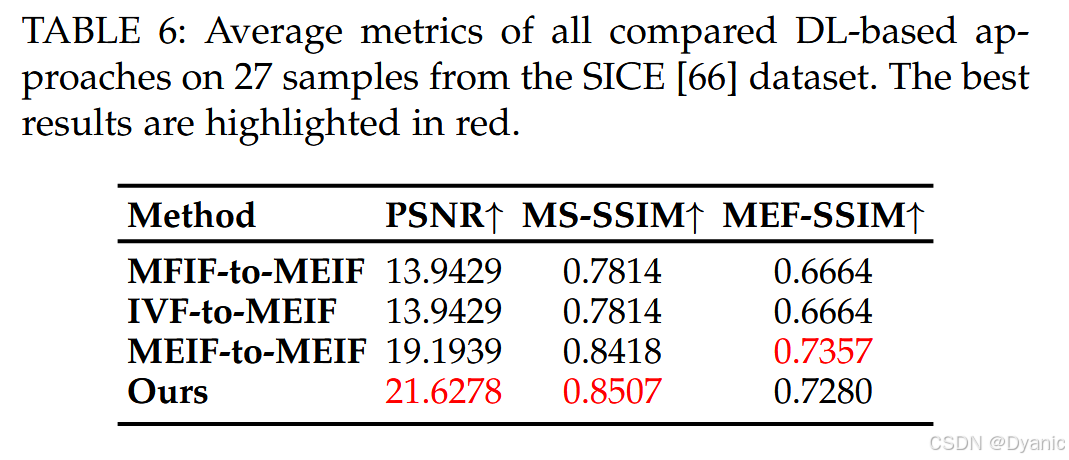
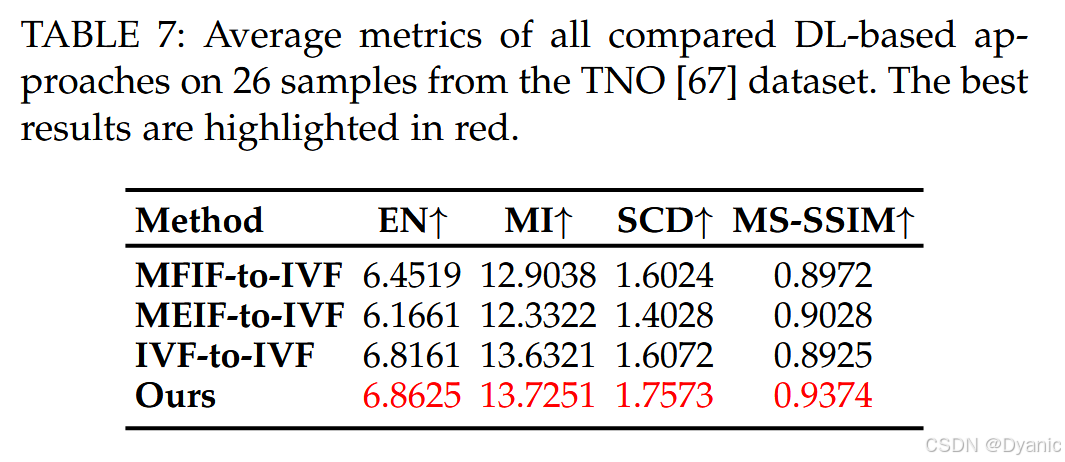
为验证所提出序列式迁移框架的有效性,我们在两个任务(MEIF 与 IVF)上基于 FRUFN 进行了系列消融实验。在 MEIF 与 IVF 任务中,我们对比了三种独立训练(分别针对 MFIF、MEIF、IVF)模型的直接测试结果,与采用序列式梯度迁移训练得到的模型结果。MEIF 与 IVF 任务的定量结果分别见表 6 与表 7。由表可见,序列式梯度迁移学习能够提升 MEIF 与 IVF 两个任务的性能。
4.8 消融实验:网络结构
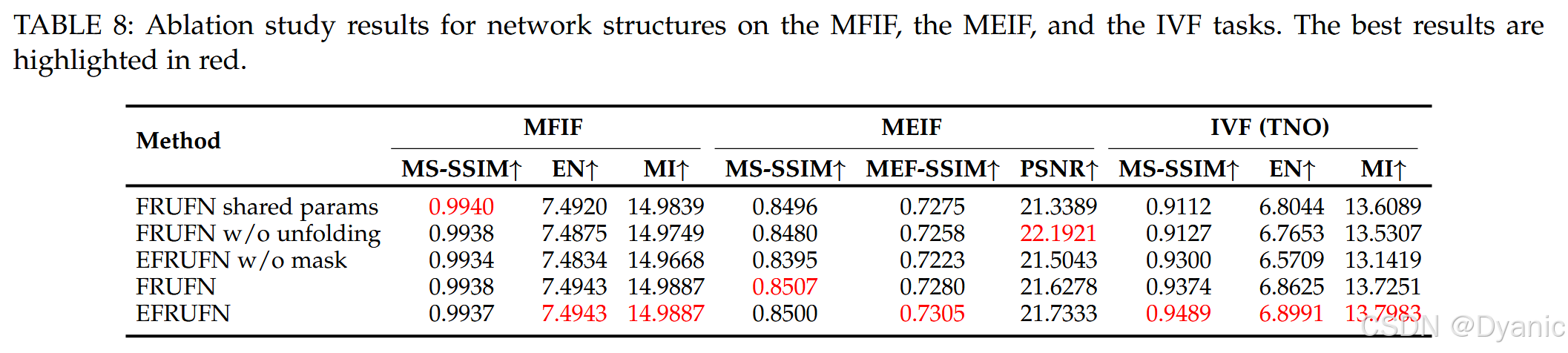
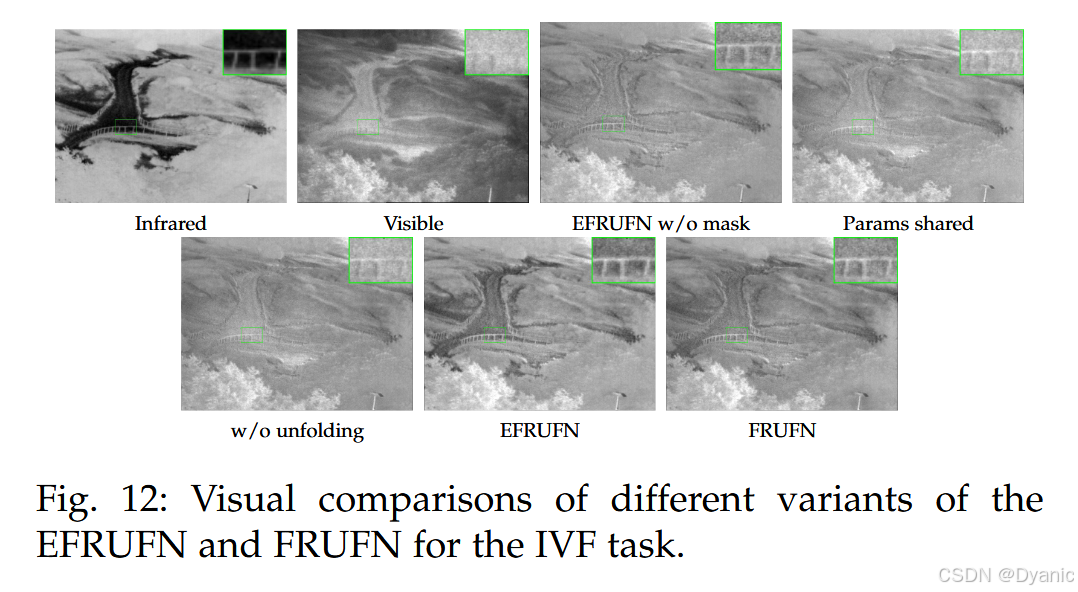
本文提出展开范式与动态可学习掩码以增强模型的泛化能力。为研究这些新设计的作用,我们进行了数值与视觉两类消融实验。更具体地,我们额外训练了 FRUFN 与 EFRUFN 的三个变体模型,分别通过移除展开范式或移除动态可学习掩码来构造。表 8 展示了数值消融实验结果。由表可见,去除所提出机制会导致 IVF 与 MIF 任务性能下降,而对 MFIF 任务影响较小。此外,我们在图 12 中给出了 IVF 任务上的视觉消融结果。图中显示,省略展开范式或改用简单的参数共享会降低模型表征能力,从而导致融合图像结构过度模糊。进一步地,若缺少动态可学习掩码,模型无法区分前景与背景,导致图像对比度明显下降。
4.9 EFRUFN 与 FRUFN 的效率比较
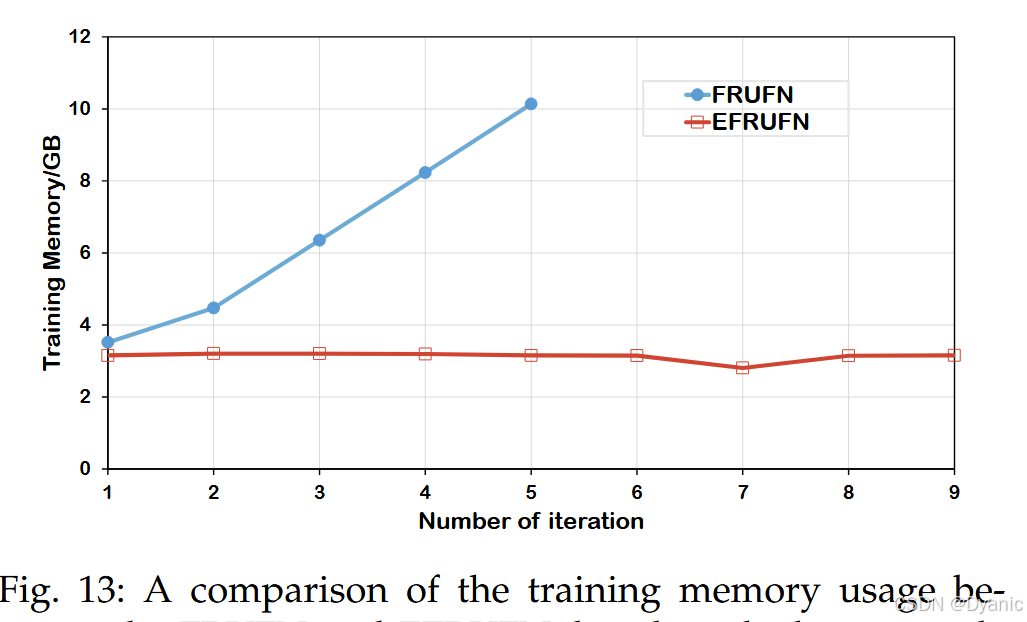
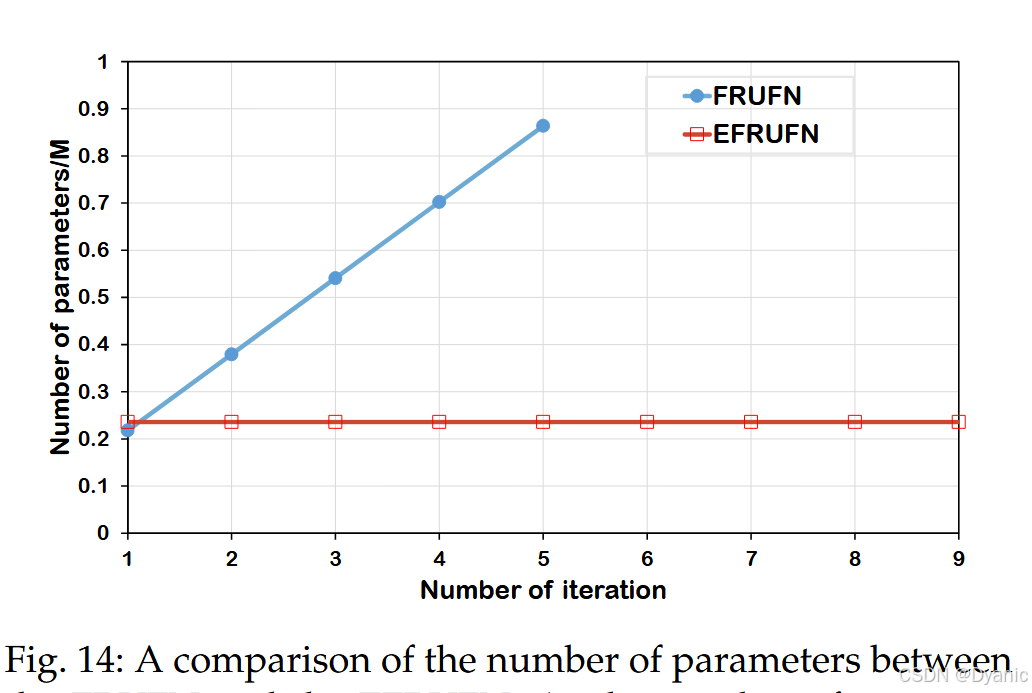
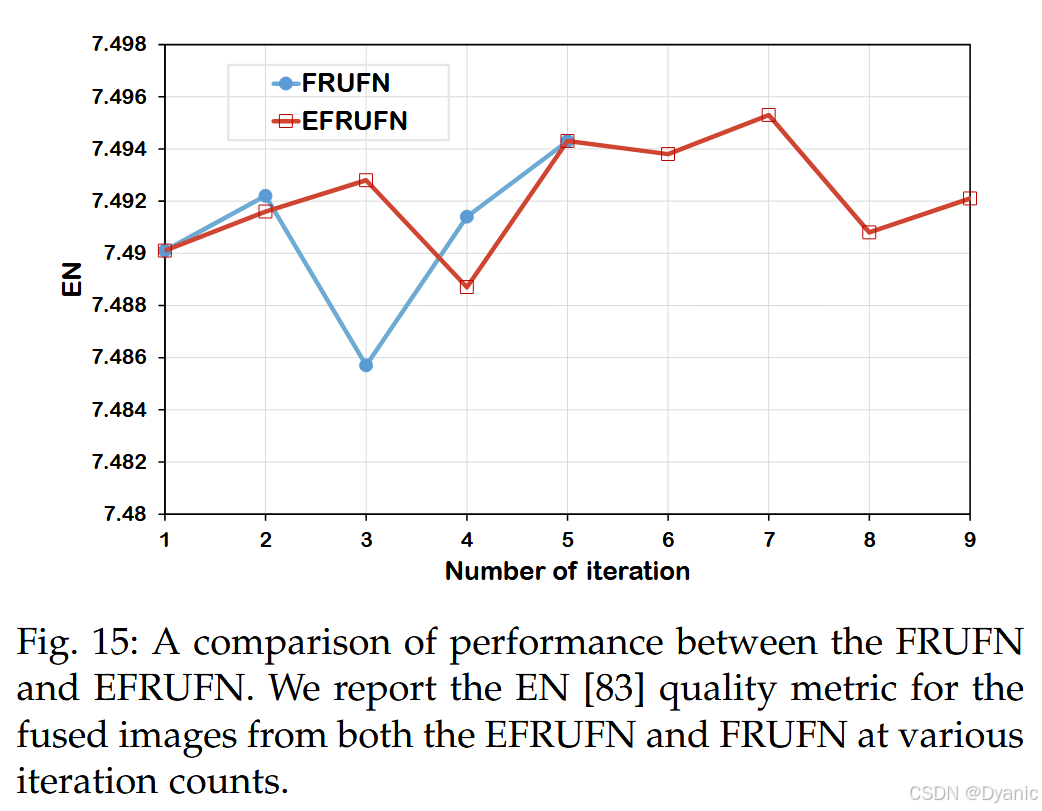
本节比较 EFRUFN 与 FRUFN 的效率。图 13 给出了 batch size 设为 4 时的总训练内存。可以明显看出,FRUFN 的内存消耗随迭代次数线性增长,而 EFRUFN 的内存使用量与迭代次数无关、保持恒定。由于 GPU 内存限制,FRUFN 最多只能进行 5 次迭代,而 EFRUFN 可支持无限次迭代。因此,EFRUFN 比 FRUFN 更具内存效率。图 14 显示,EFRUFN 的参数量随迭代次数增加保持稳定;相反,FRUFN 的参数量随迭代次数线性增长,这表明 EFRUFN 在参数效率方面优于 FRUFN。此外,图 15 表明 EFRUFN 与 FRUFN 在不同迭代次数下的性能相近。然而,FRUFN 受 GPU 内存限制只能迭代 5 次,而 EFRUFN 可在无此限制下迭代更多次数,从而可能获得更好的性能。综上,EFRUFN 在训练时需要更少模型参数与更少 GPU 内存,同时可达到与 FRUFN 相当的性能。
5 结论
本文提出了一种通用图像融合的综合方法,在模型训练与网络结构设计方面均引入了创新。在模型训练方面,我们提出了序列式梯度迁移框架,利用跨任务结构互补信息,显著提升了模型对源图像结构完整性的保留能力。在网络设计方面,我们提出了一种基于核心融合原则深度展开的通用图像融合网络,简化了传统上耗时且劳动密集的网络设计过程。大量实验表明,与现有方法相比,我们的方法能够生成具有更优结构细节保留的融合结果。此外,所提出方法展现出很强的泛化能力,即使面对此前未见过的图像融合任务也能取得良好表现。