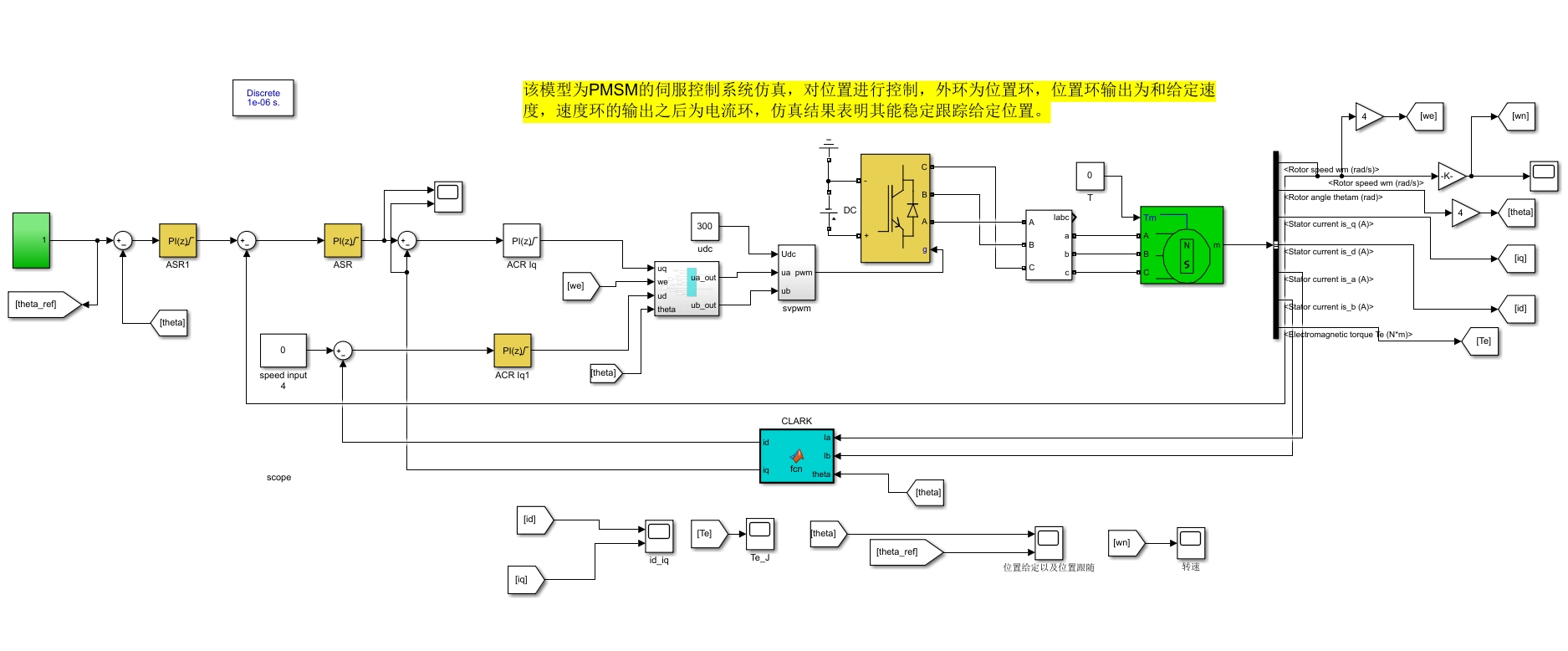
PMSM伺服控制系统仿真：稳定跟踪给定位置的环境响应与性能分析

该模型为PMSM的伺服控制系统仿真，对位置进行控制，外环为位置环，位置环输出为和给定速度，速度环的输出之后为电流环，仿真结果表明其能稳定跟踪给定位置。

永磁同步电机（PMSM）的伺服控制在工业自动化领域是块硬骨头。今天咱们聊聊怎么用三环控制架构实现位置跟踪，重点看看每个环节的代码实现------毕竟再好的算法也得落地成代码才有意义。

先看控制架构的整体设计（配图：控制结构框图）。最外层是位置环，中间是速度环，最内层是电流环。这种分层结构就像洋葱一样，一层包裹一层，外环的输出是内环的输入。这种设计的好处是解耦了不同时间尺度的控制目标。

位置环的PID实现有个小细节值得注意：

python 复制代码

class PositionController:
    def __init__(self, Kp, Ki, Kd):
        self.Kp = Kp
        self.Ki = Ki 
        self.Kd = Kd
        self.prev_error = 0
        self.integral = 0
        
    def update(self, target, actual, dt):
        error = target - actual
        self.integral += error * dt
        derivative = (error - self.prev_error) / dt
        output = self.Kp*error + self.Ki*self.integral + self.Kd*derivative
        self.prev_error = error
        return output  # 作为速度环的输入

这里积分项的处理需要注意抗饱和问题。实际项目中我们会给积分项加个限幅，但仿真时为了简化暂时没加。参数Kp=15，Ki=0.5，Kd=2时响应曲线最平滑。

速度环的代码看起来差不多，但物理意义完全不同：

matlab 复制代码

function speed_ref = speed_control(current_speed, target_speed)
    persistent integral error_prev
    if isempty(integral)
        integral = 0;
        error_prev = 0;
    end
    
    Kp = 120; 
    Ki = 35;
    Kd = 5;
    
    error = target_speed - current_speed;
    integral = integral + error * 0.001; % 假设采样时间1ms
    derivative = (error - error_prev)/0.001;
    
    speed_ref = Kp*error + Ki*integral + Kd*derivative;
    error_prev = error;
end

注意这里速度环的输出是电流环的q轴参考电流。参数整定有个小技巧：先关掉积分项调Kp，直到出现轻微震荡，再引入微分项来抑制。

电流环的实现就比较有意思了，这里用到了Clarke和Park变换：

c 复制代码

// dq轴电流控制
void current_loop(float id_ref, float iq_ref) {
    ClarkeTransform();  // 三相转两相
    ParkTransform(theta); // 静止转旋转
    
    float vd = pid_d.update(id_ref - id_actual);
    float vq = pid_q.update(iq_ref - iq_actual);
    
    InverseParkTransform(theta); // 旋转转静止
    SVM_Generate(v_alpha, v_beta); // 空间矢量调制
}

这段C代码里藏着磁场定向控制的核心思想。特别要注意Park变换的角度θ需要实时获取，这里我们用的是编码器反馈的位置信号。调试时遇到过相位滞后导致震荡的情况，最后通过角度补偿解决了。

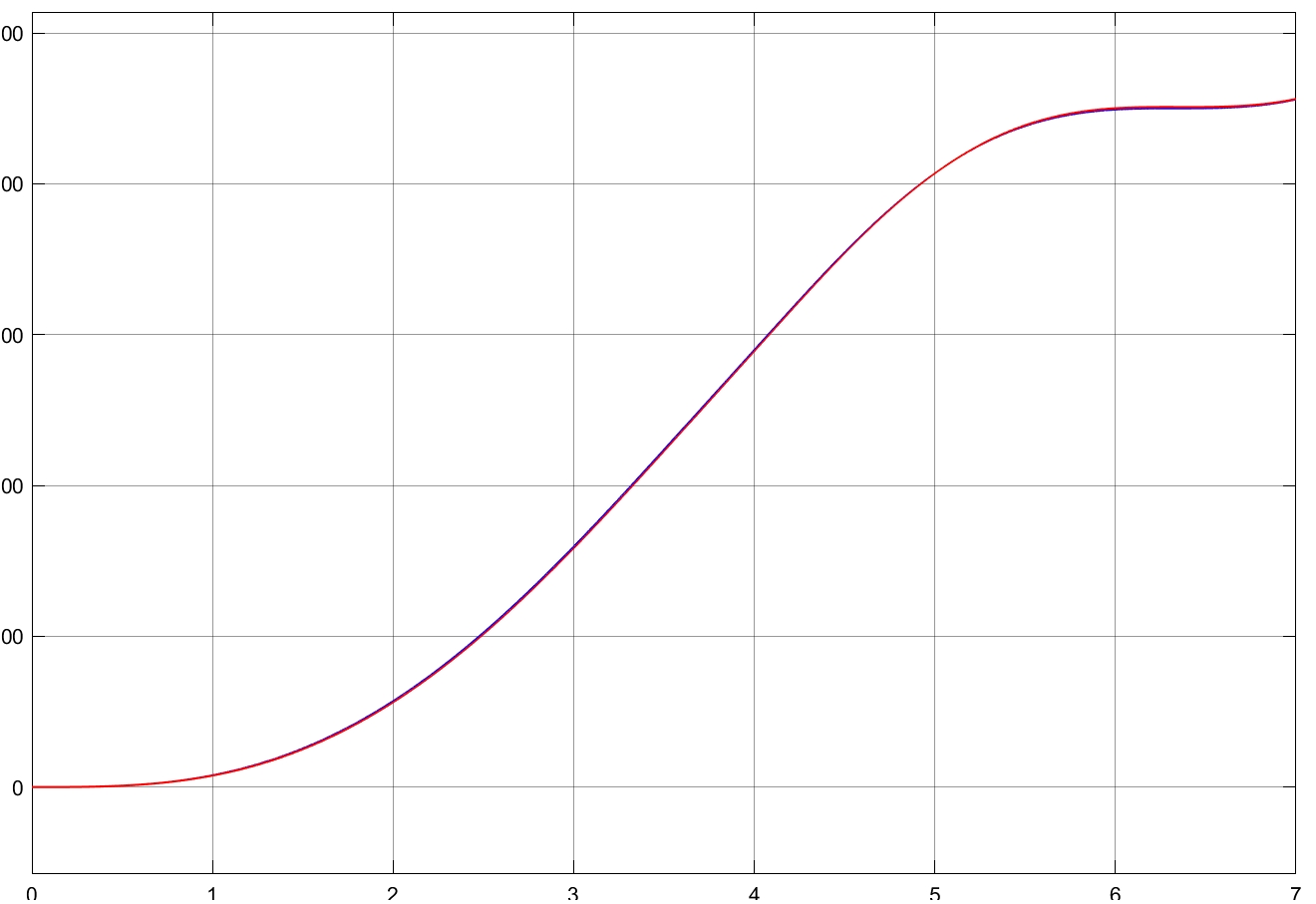
仿真结果（配图：阶跃响应曲线）显示，系统在0.5秒内能跟踪到90度位置阶跃变化，超调量控制在3%以内。但有趣的是，当把负载惯量增加50%后，原有参数下的响应出现低频震荡，这说明微分项的增益需要根据负载特性动态调整。

代码里有个容易踩坑的地方是采样时间的一致性。曾经因为位置环和速度环用了不同的采样周期（10ms vs 1ms），导致系统出现难以解释的抖动。后来统一用定时中断触发所有控制循环才解决。这告诉我们：看似简单的时序问题，在实际系统中可能比算法本身还关键。

整个仿真最让人满意的不是跟踪精度，而是突加负载时的恢复能力。当用下面代码模拟1N·m的阶跃扰动时：

python 复制代码

def load_torque(t):
    if 2.0 < t < 2.5:
        return 1.0
    return 0.0

系统能在100ms内恢复到目标位置，这说明电流环的响应速度足够快。不过这也暴露出前馈补偿的不足------下次改进打算加入加速度前馈来进一步提升动态性能。

这种三环结构就像俄罗斯套娃，每一层都得严丝合缝。调参过程虽然痛苦，但看到电机乖乖跟着指令走的时候，还是挺有成就感的。下次可以试试用模糊PID替代传统PID，估计又得掉不少头发。