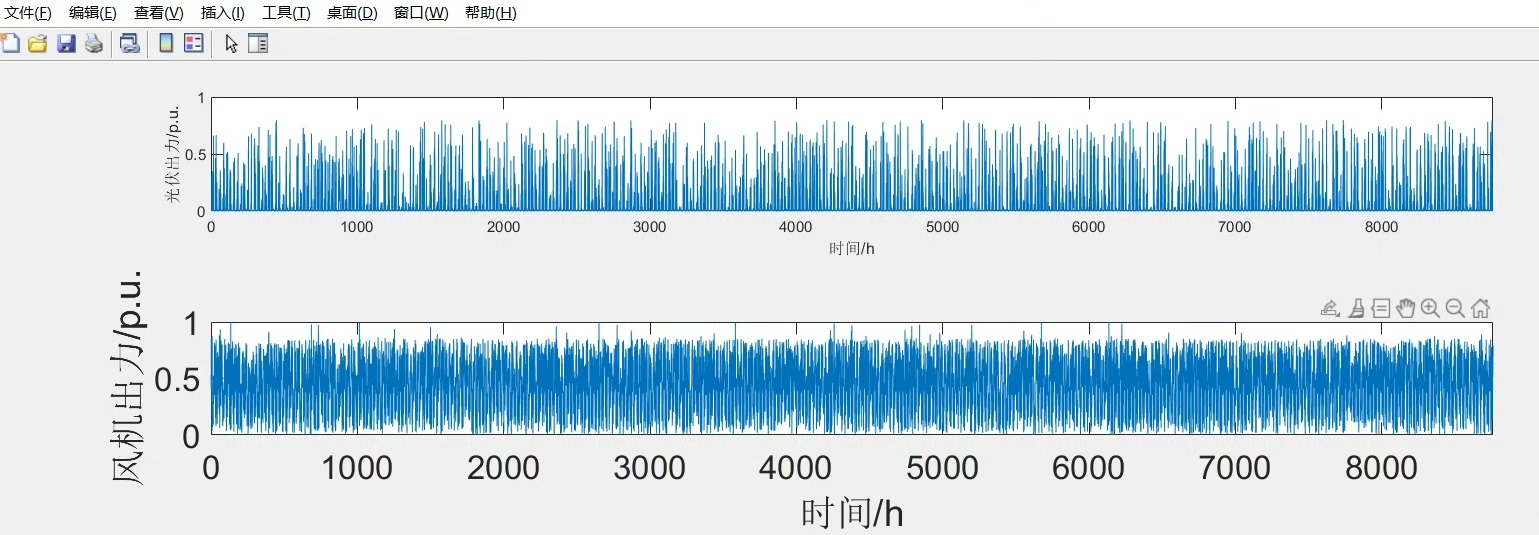
基于Copula理论与K-means的考虑风光出力相关性的风光场景生成与削减 关键词:Copula 场景生成 风光出力相关性 k-means算法 参考文档: [1]《基于核密度估计和 Copula 函数的风、光出力场景生成》 [2]《融合风光出力场景生成的多能互补微网系统优化配置_白凯峰》 仿真软件: matlab 主要内容:代码主要做的是风光场景生成的内容,与目前大部分的基于蒙特卡洛或者拉丁超立方等方法不同,代码在场景生成的过程中考虑了风光出力的相关性,并通过Frank-Copula函数描述风光之间的相关性,从而生成具有相关性的风光场景!最后,通过k-means算法,对生成的大规模风光场景进行削减,最终得到五个场景,并给出各个场景的概率! 注意事项:代码注释详细。 程序运行稳定,仿真结果如下截图所示。 靠谱运行可靠值得信赖。
最近在研究风光场景生成相关的内容,发现了一个超有意思的代码,它是基于Copula理论与K-means来考虑风光出力相关性的。
代码核心亮点
这个代码和常见的基于蒙特卡洛或者拉丁超立方等方法不太一样哦。它在生成场景的过程中,着重考虑了风光出力的相关性,并且通过Frank-Copula函数来描述风光之间的这种相关性,以此生成具有相关性的风光场景。这一点真的很独特!
Copula理论与Frank-Copula函数
Copula理论在这里起到了关键作用。简单来说,它能把多维随机变量的联合分布分解为多个一维边缘分布和一个Copula函数。Frank-Copula函数就是其中一种用来描述变量之间相关性的函数。
matlab
% 假设这里有风光出力的边缘分布数据
wind_data = [......];
solar_data = [......];
% 使用Frank-Copula函数来描述相关性
theta =......; % 相关参数
copula_function = frankCopula(theta);
joint_distribution = copulaFunction(copula_function, wind_data, solar_data);在这段代码里,首先我们有了风光出力各自的边缘分布数据。然后通过设置theta参数来定义Frank-Copula函数,接着利用这个函数得到联合分布joint_distribution。这个联合分布就包含了风光出力之间的相关性信息啦。
k-means算法进行场景削减
生成了大规模的风光场景后,代码又通过k-means算法对这些场景进行削减。
matlab
% 假设生成了大量的风光场景数据scenarios
scenarios = [......];
k = 5; % 设定要削减到的场景数量为5
[idx, C] = kmeans(scenarios, k);
% 统计每个聚类的概率
unique_labels = unique(idx);
probabilities = histcounts(idx, unique_labels) / length(idx);这里,我们先有了所有的风光场景数据scenarios。然后设定k = 5,表示我们要把场景削减到5个。通过kmeans函数,它会自动将这些场景数据聚成5类,每一类就是我们最终得到的一个场景。最后通过统计每个聚类中的数据点数量,再除以总数据点数量,就得到了各个场景的概率probabilities。
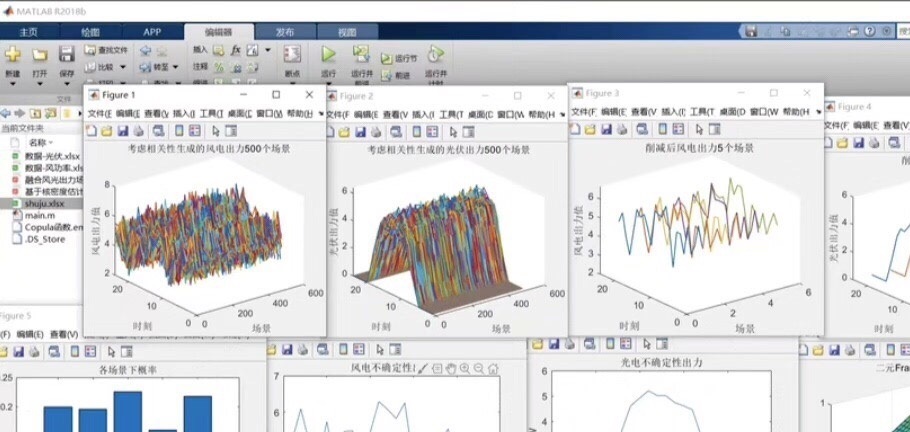
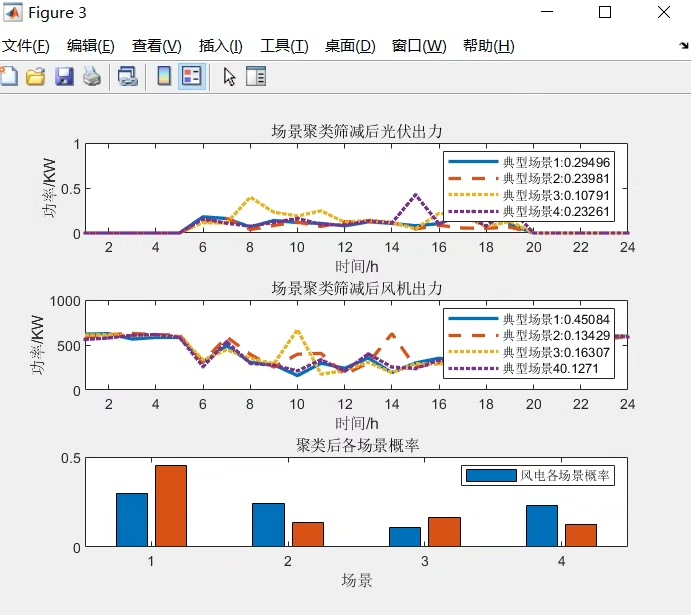
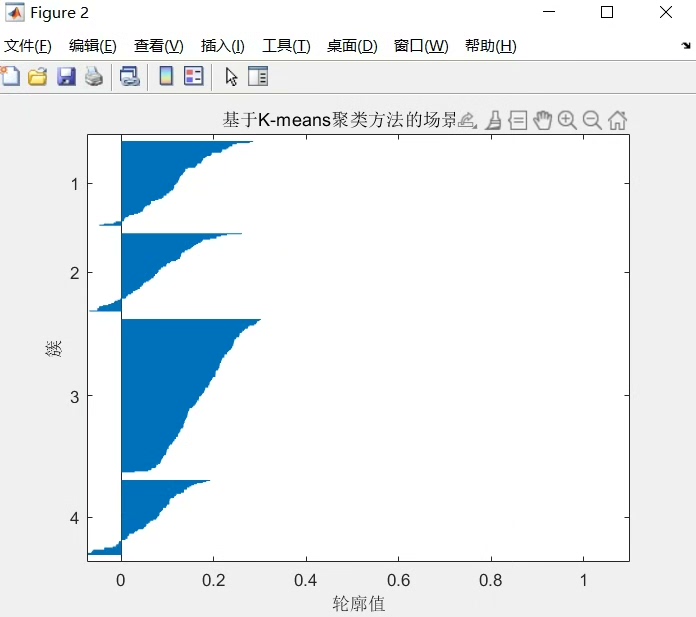
运行结果展示
这个程序运行得相当稳定,仿真结果也很直观。从截图中可以清晰地看到生成的风光场景以及经过削减后得到的五个场景,每个场景还有对应的概率显示。
不得不说,这种基于Copula理论与K-means的方法真的为风光场景生成与削减提供了一种很新颖且有效的思路。它让我们能更准确地考虑风光出力之间的相关性,得到更符合实际情况的场景结果。大家要是对风光发电相关的研究感兴趣,不妨也来试试这个方法呀!