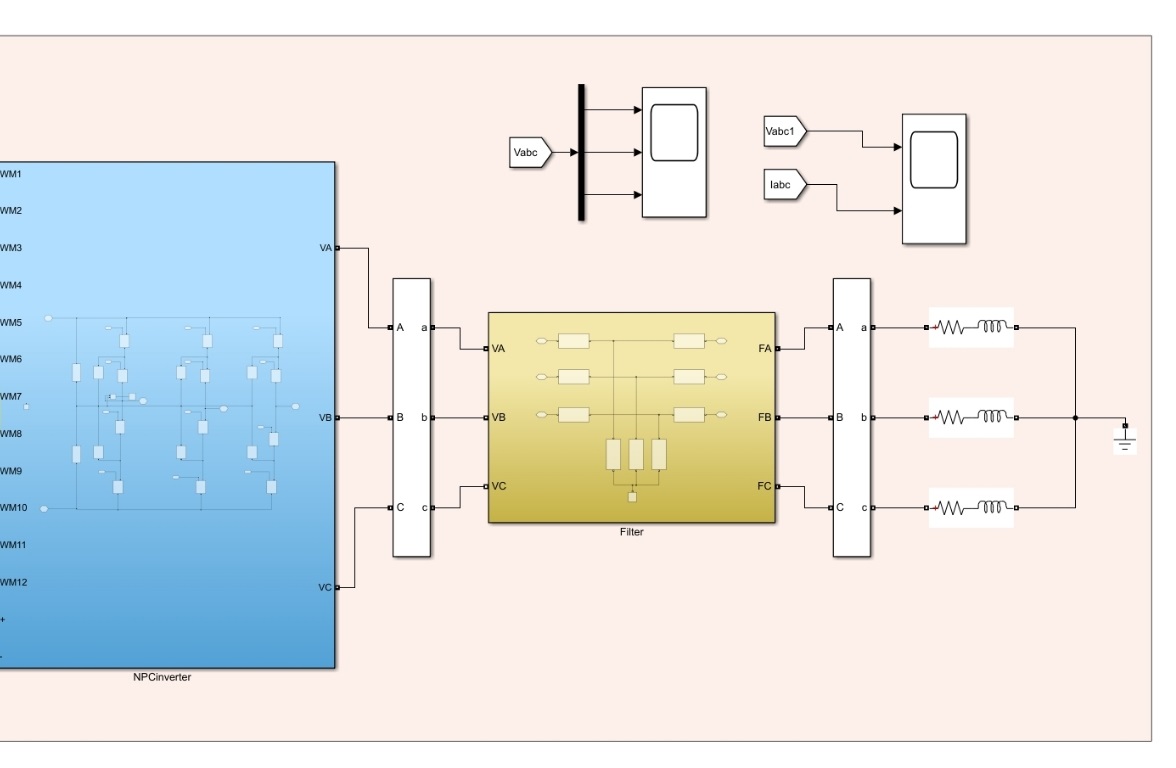
三电平NPC逆变器矢量控制（SVPWM）matlab2021a 采用矢量控制，大扇区、小扇区、...

三电平NPC逆变器矢量控制（SVPWM）matlab2021a 采用矢量控制，大扇区、小扇区、矢量作用时间等均用程序编写，可以得到马鞍波调制波形逆变器输出三电平相电压波形，五电平线电压波形，经过滤波器后，可以得到对称的三相电压，电流

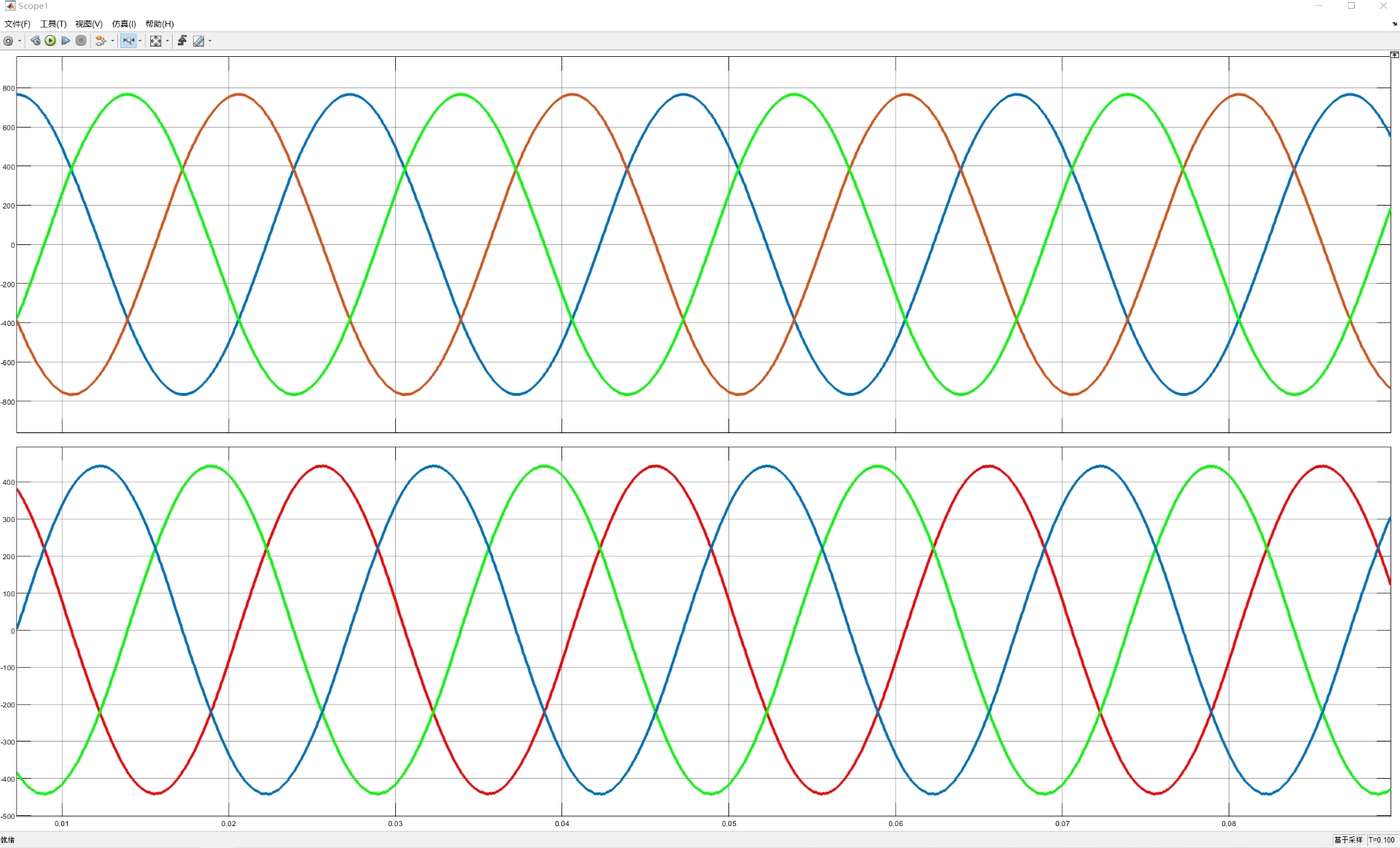
三电平NPC逆变器的矢量控制搞起来就像在玩一场精密的时间分配游戏。最近在Matlab2021a里折腾SVPWM实现时发现，想要让马鞍波完美呈现，关键得处理好空间矢量的时空分布。这里分享几个核心代码片段，看看怎么用程序实现从矢量分配到波形生成的完整链路。

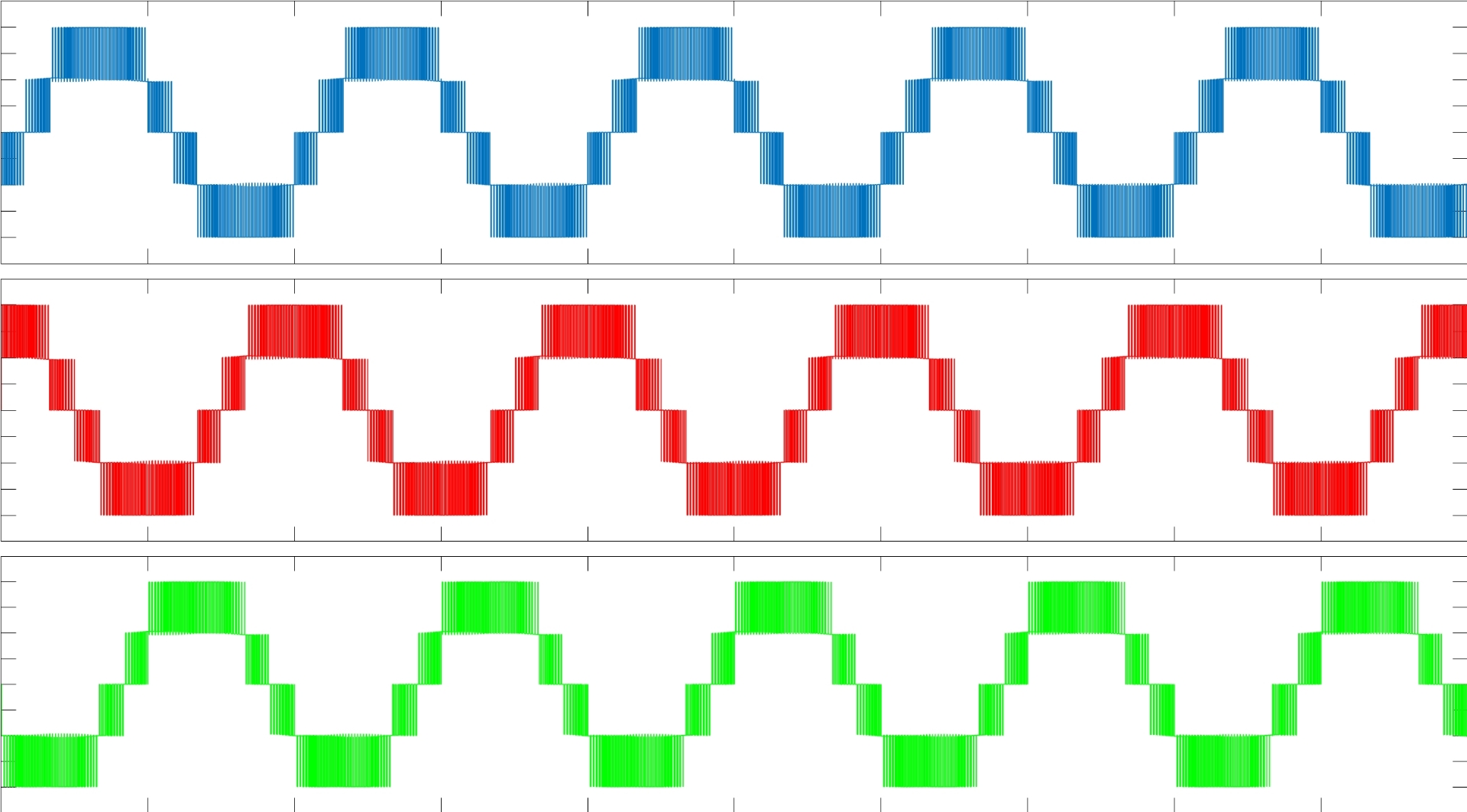
先说扇区判断这个头疼问题。传统三电平有6个大扇区，每个大扇区又包含4个小扇区。咱们用Clarke变换后的Vα、Vβ坐标来定位参考矢量：

matlab 复制代码

function sector = getSector(v_alpha, v_beta)
    theta = mod(atan2(v_beta, v_alpha), 2*pi);
    sector = floor(theta/(pi/3)) + 1; 
    % 这里可以加个边界条件处理，防止越界
    if sector >6, sector = 1; end 
end

这段代码把360度空间切成6块披萨，但实际运行时会发现矢量跳变的问题------特别是当参考矢量在扇区边界附近抖动时。后来加了滞后比较才稳定下来，就像给矢量运动装了缓冲垫。

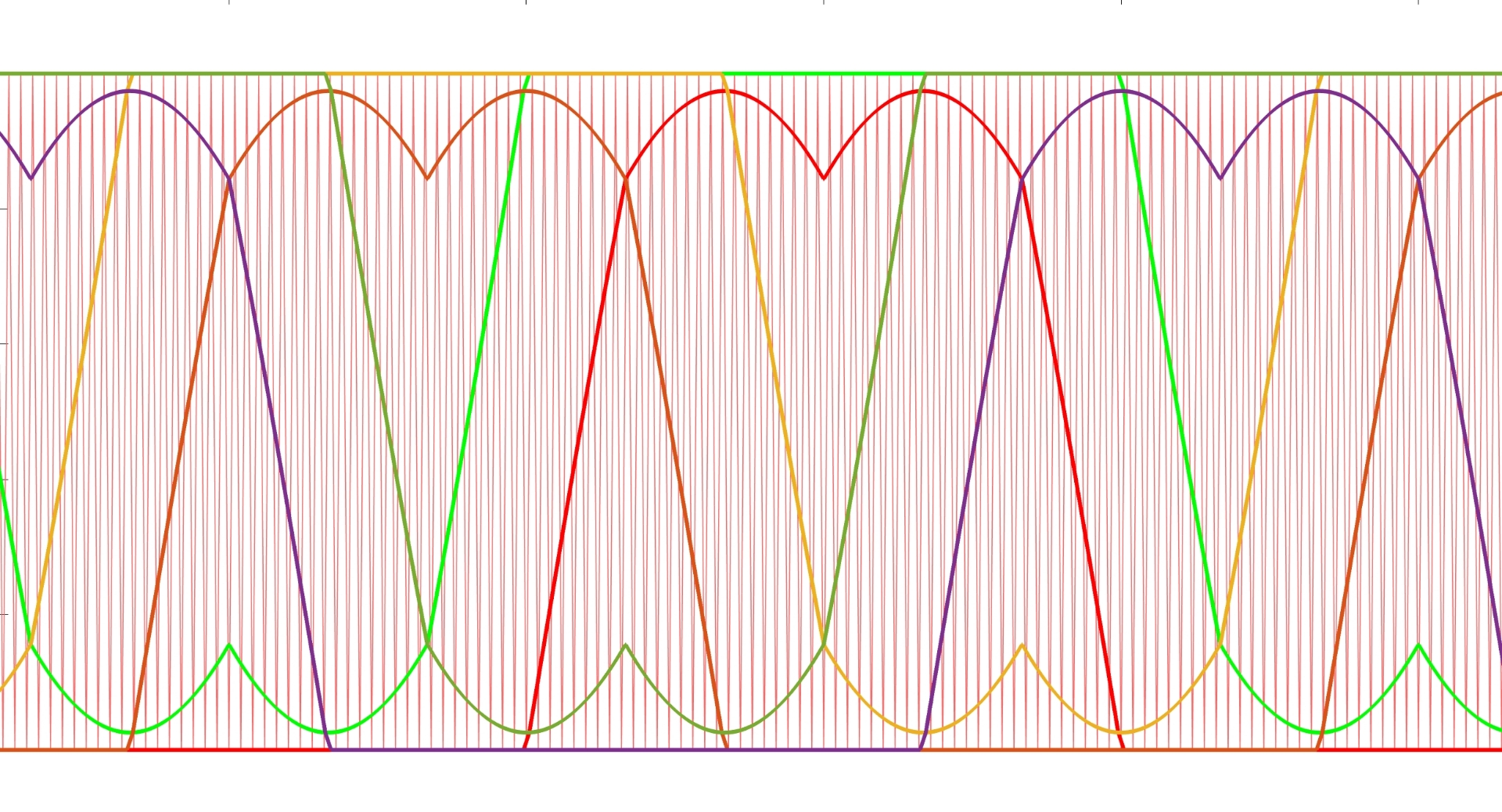
时间分配算法才是真正的重头戏。每个采样周期要计算三个最近矢量的作用时长，这里用到了伏秒平衡原理：

matlab 复制代码

Ts = 1e-4; % 开关周期
Vdc = 600; 
t1 = (v_alpha * sin(pi/3 - theta) - v_beta * cos(pi/3 - theta)) * Ts / (Vdc * sin(pi/3));
t2 = (v_beta * cos(theta) - v_alpha * sin(theta)) * Ts / (Vdc * sin(pi/3));
t0 = Ts - t1 - t2;
% 这里常出现负时间问题，需要做饱和处理
[t1, t2] = deal(max(t1,0), max(t2,0));

调试时发现当参考矢量接近区域边界时，t1或t2容易变负数。这时候需要启动修正策略，比如按比例缩放有效矢量时间，保证总时长不变。

生成马鞍波的时候，PWM比较值计算是个技术活。五电平线电压的实现关键在于相邻矢量的交替作用：

matlab 复制代码

function cmp_val = genCompare(v_ref, sector)
    % 三电平特有的中点电位补偿逻辑
    cmp_base = [0.25 0.5 0.75]; 
    % 根据扇区选择矢量作用顺序
    seq_matrix = [1 2 3; 2 3 4; ... ]; 
    active_seq = seq_matrix(sector,:);
    % 时间分配结果映射到具体开关状态
    t_seq = [t0/4, t1/2, t2/2, t0/4]; 
    % 生成三角载波比较值
    cmp_val = cumsum(t_seq) .* [cmp_base(active_seq(1)), ... ];
end

这里有个坑------中点电压平衡问题。后来在代码里加了个滞环控制，实时监测上下电容电压，动态调整小矢量选择策略，波形畸变明显改善。

滤波器的设计直接影响最终波形质量。用二阶LC滤波时，截止频率要设在开关频率的1/10左右：

matlab 复制代码

L = 3e-3; % 3mH
C = 10e-6; % 10μF
f_sw = 10e3; 
% 临界阻尼设计避免震荡
R_damp = 2*sqrt(L/C); 
% 实际用传递函数验证相位裕度
sys = tf(1,[L*C L/R_damp 1]);
bode(sys); % 检查-3dB点是否符合预期

最后跑出来的相电压波形呈现典型的三电平台阶，线电压则展现出五电平结构。电流波形经过滤波后THD能控制在3%以内，特别是轻载时依然保持光滑的正弦形态。有个有趣的发现：当调制比超过0.9时，马鞍波的凹陷特征会突然变得明显，就像被捏扁的正弦波，这时候要特别注意过调制处理策略。