基于阶梯碳交易的含P2G - CCS耦合和燃气掺氢的虚拟电厂优化调度探索

基于阶梯碳交易的含P2G-CCS耦合和燃气掺氢的虚拟电厂优化调度参考文献：基于阶梯碳交易的含P2G-CCS耦合和燃气掺氢的虚拟电厂优化调度 matlab+yalmip+cplex 主要内容：代码针对 P2G-CCS 耦合和燃气掺氢子系统，建立了掺氢燃气轮机、掺氢燃气锅炉、两段式电转气和碳捕集系统的数学模型；其次，在低碳政策层面，建立了阶梯碳交易模型对系统碳排放进行约束；最后，在建模基础上，提出了以碳交易成本、购气和煤耗成本、碳封存成本、机组启停成本和弃风成本之和最低为目标函数的优化调度策略。附带详细的复现过程说明文档！出图比所发文章更多更细致，额外考虑了各主体的功率平衡，复现了各情景下的情况。

最近在研究基于阶梯碳交易的含P2G - CCS耦合和燃气掺氢的虚拟电厂优化调度相关内容，和大家分享一下我的心得。

这次研究主要借助matlab + yalmip + cplex工具来实现。咱们先从代码针对的子系统数学模型说起。

一、子系统数学模型

1. 掺氢燃气轮机

它的运行特性需要精确建模，假设其输出功率 $P*{gt}$ 与输入的掺氢燃气量 $F*{gt}$ 以及氢气比例 $x_{h2}$ 相关。在Matlab代码中，可以这样简单示意：

matlab 复制代码

% 假设已知的一些参数
eta_gt = 0.3; % 燃气轮机效率
LHV_gas = 50000; % 天然气低热值
LHV_h2 = 120000; % 氢气低热值

% 输入变量
F_gt = 10; % 输入的掺氢燃气量
x_h2 = 0.2; % 氢气比例

% 计算输出功率
P_gt = eta_gt * ( (1 - x_h2) * LHV_gas + x_h2 * LHV_h2 ) * F_gt;

这里通过燃气轮机效率eta_gt，以及天然气和氢气的低热值，结合输入的燃气量和氢气比例，算出输出功率。实际模型肯定更复杂，比如还得考虑温度、压力等因素对效率的影响，但这能让大家有个基本概念。

2. 掺氢燃气锅炉

它的模型重点在于热量转换，假设其产生的热量 $Q*{gb}$ 与输入的掺氢燃气量 $F*{gb}$ 和氢气比例 $x_{h2}$ 有关。代码示例如下：

matlab 复制代码

% 假设已知参数
eta_gb = 0.8; % 燃气锅炉效率

% 输入变量
F_gb = 8; % 输入的掺氢燃气量

% 计算产生的热量
Q_gb = eta_gb * ( (1 - x_h2) * LHV_gas + x_h2 * LHV_h2 ) * F_gb;

这个代码通过燃气锅炉效率eta_gb来计算产生的热量，实际中也需要考虑更多细节，比如不同工况下的效率变化等。

3. 两段式电转气和碳捕集系统

对于两段式电转气，涉及到电转气效率、不同阶段的转换关系等。碳捕集系统则要考虑捕集效率、成本等因素。假设电转气总效率为 $\\eta*{p2g}$ ，输入电功率 $P*{in}$ ，产生的合成气量 $F_{s}$ ：

matlab 复制代码

% 假设已知参数
eta_p2g = 0.6;

% 输入变量
P_in = 20; % 输入电功率

% 计算合成气量
F_s = eta_p2g * P_in / LHV_s; % LHV_s为合成气低热值

碳捕集系统假设捕集效率为 $\\eta*{ccs}$ ，碳排放 $E$ ，捕集的碳量 $E*{captured}$ ：

matlab 复制代码

% 假设已知参数
eta_ccs = 0.8;

% 输入变量
E = 100; % 碳排放

% 计算捕集的碳量
E_captured = eta_ccs * E;

二、阶梯碳交易模型

在低碳政策层面，建立阶梯碳交易模型来约束系统碳排放。简单来说，碳排放总量 $E*{total}$ 如果在某个阈值 $E* {threshold1}$ 以下，碳交易价格为 $C*{1}$ ；超过 $E* {threshold1}$ 但在 $E*{threshold2}$ 以下，碳交易价格为 $C*{2}$ ，以此类推。Matlab代码中可以通过条件判断来实现：

matlab 复制代码

% 假设已知参数
E_threshold1 = 500;
E_threshold2 = 800;
C_1 = 10;
C_2 = 20;

% 计算出的碳排放总量
E_total = 600;

if E_total <= E_threshold1
    C = C_1;
elseif E_total <= E_threshold2
    C = C_2;
else
    % 更多阶梯的情况
    C = 30;
end

三、优化调度策略

在上述建模基础上，提出优化调度策略，目标函数是让碳交易成本、购气和煤耗成本、碳封存成本、机组启停成本和弃风成本之和最低。假设碳交易成本 $Cost*{carbon}$ 、购气和煤耗成本 $Cost* {gas\\*coal}$ 、碳封存成本 $Cost* {sequestration}$ 、机组启停成本 $Cost*{start\\* stop}$ 、弃风成本 $Cost*{wind\\*curtailment}$ ：

matlab 复制代码

Cost_carbon = C * E_total;
Cost_gas_coal = price_gas * F_gas + price_coal * M_coal; % price_gas和price_coal分别为气价和煤价，F_gas为购气量，M_coal为煤耗量
Cost_sequestration = cost_sequestration * E_captured; % cost_sequestration为单位碳封存成本
Cost_start_stop = sum(start_stop_cost); % start_stop_cost为每次机组启停成本数组
Cost_wind_curtailment = price_wind * P_wind_curtailment; % price_wind为风电价格，P_wind_curtailment为弃风量

Total_cost = Cost_carbon + Cost_gas_coal + Cost_sequestration + Cost_start_stop + Cost_wind_curtailment;

四、复现过程及出图

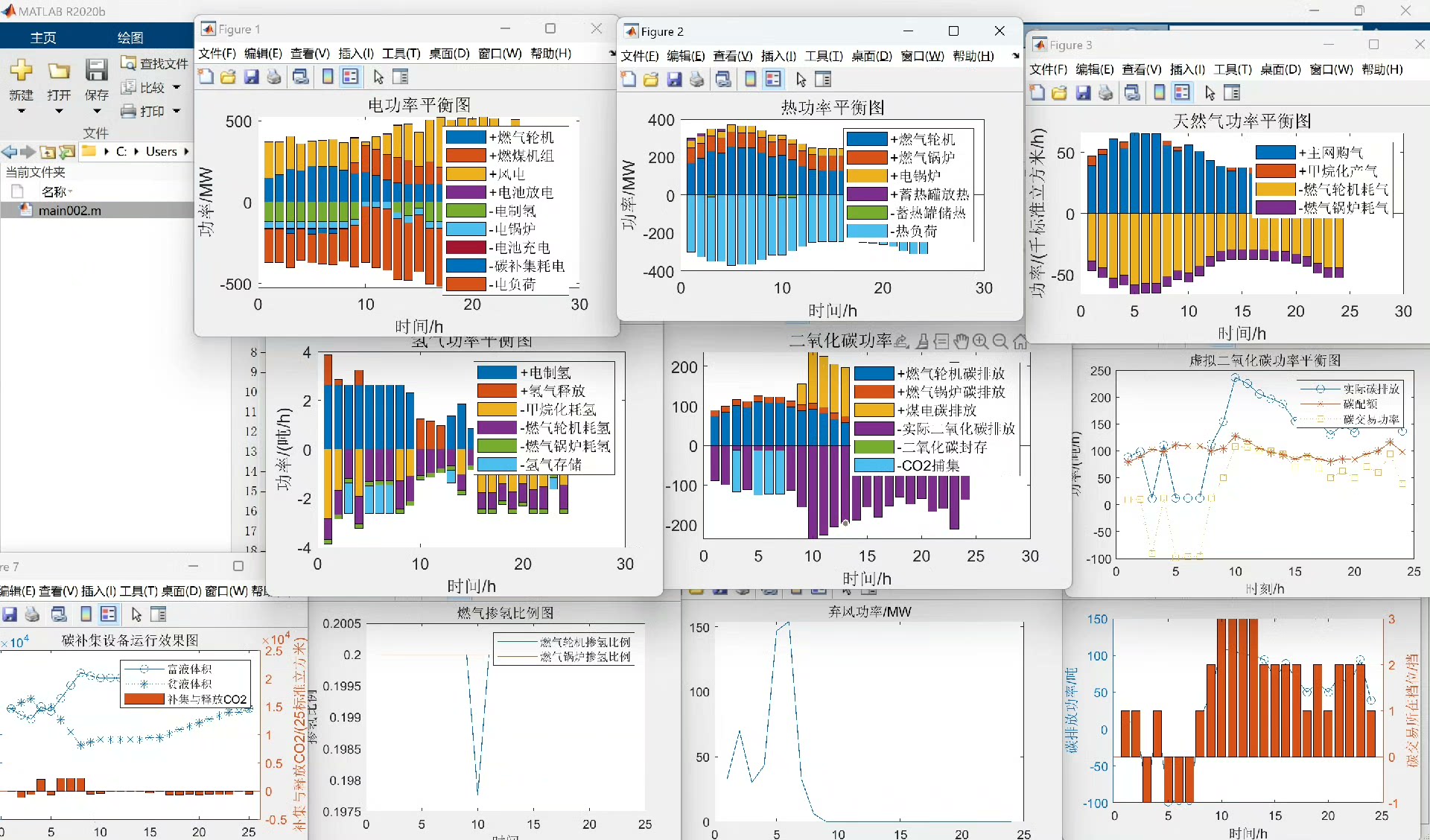
这次还附带详细的复现过程说明文档哦。在出图方面，比所发文章更多更细致，而且额外考虑了各主体的功率平衡，复现了各情景下的情况。比如通过Matlab的绘图函数plot，我们可以绘制不同情景下各子系统的功率变化，像这样：

matlab 复制代码

% 假设已经计算出不同时间点的子系统功率
time_points = 1:10;
P_gt_values = [10, 12, 15, 13, 14, 16, 18, 17, 15, 14];
P_gb_values = [8, 9, 10, 9, 11, 12, 11, 10, 9, 8];

figure;
plot(time_points, P_gt_values, 'r', 'DisplayName', '燃气轮机功率');
hold on;
plot(time_points, P_gb_values, 'b', 'DisplayName', '燃气锅炉功率');
xlabel('时间点');
ylabel('功率 (MW)');
legend;
title('不同时间点燃气轮机和燃气锅炉功率变化');

这样就能直观地看到不同子系统在不同时间的功率情况，对于分析系统运行状态很有帮助。

通过这些数学模型、策略以及复现过程，我们对基于阶梯碳交易的含P2G - CCS耦合和燃气掺氢的虚拟电厂优化调度有了更深入的理解和实践。希望对大家有所启发！