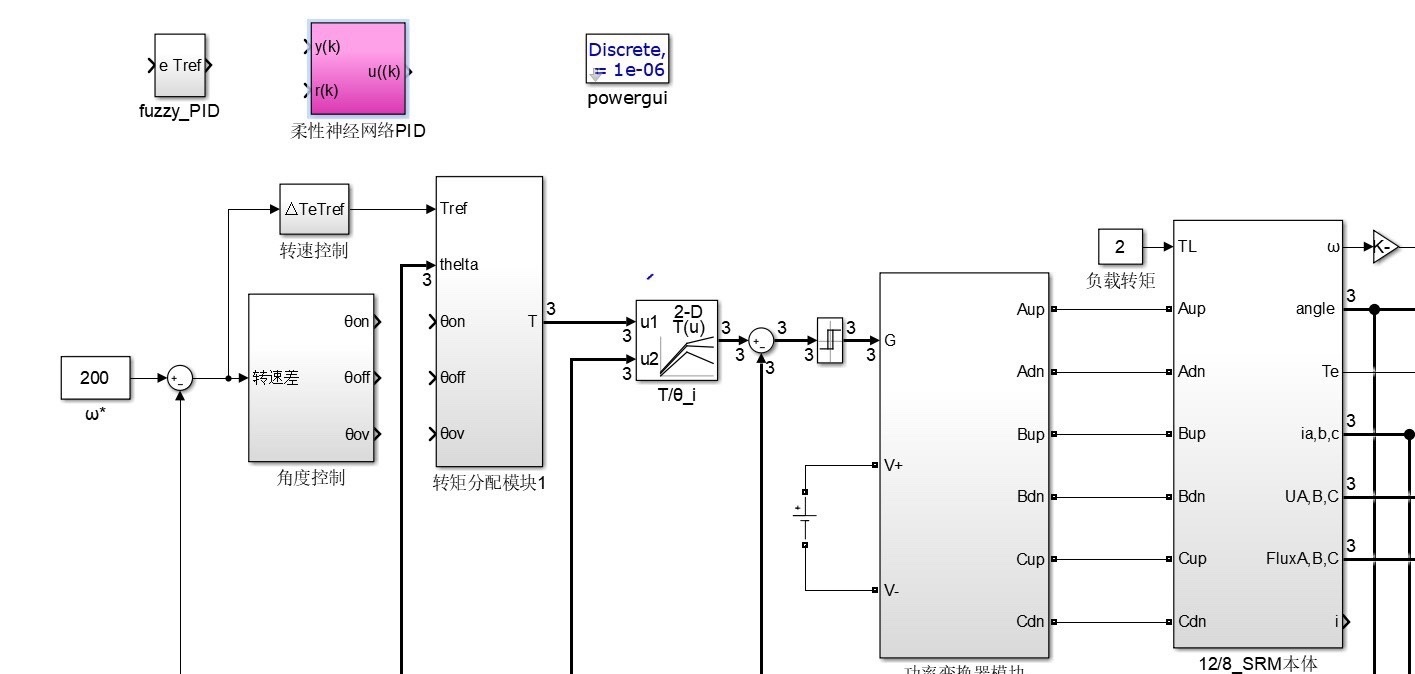
开关磁阻电机控制仿真：Matlab 2016b的探索之旅

开关磁阻电机控制仿真(matlab 2016b版本仿真模型 自用) 模型包涵： 开关磁阻电机传统控制：电流斩波控制、电压PWM控制、角度位置控制。 智能控制：12/8三相开关磁阻电机有限元分析本体建模、转矩分配函数控制、模糊PID控制、模糊角度控制、神经网络在线自适应迭代控制。 部分离线迭代算法：遗传算法优化PID、粒子群算法优化PID。 毕业研究生自用仿真模型 .

嘿，大家好！今天来和大伙分享下我在开关磁阻电机控制仿真这块的研究成果，基于Matlab 2016b版本搭建的仿真模型，超实用，研究生毕业自用的哦！

一、模型构成

（一）传统控制策略

1. 电流斩波控制

   • 电流斩波控制（CCC）的核心思路是通过斩波来限制电流。在Matlab里，我们可以通过设定电流的上下限来实现。
     matlab
% 假设电机参数已经设定好
upperlimit = 10; % 电流上限
     lower limit = 8; % 电流下限
while true
current = getcurrent(); % 获取当前电流值，这里假设get current()是获取电流的函数
if current > upperlimit
     % 关断开关，降低电流
     switch off();
elseif current < lowerlimit
     % 开通开关，升高电流
     switch on();
end
end

   • 这段代码逻辑很清晰，不断监测电流，超过上限就关开关，低于下限就开开关，从而将电流控制在一定范围内。这种控制方式能有效限制电流峰值，保护功率器件。

2. 电压PWM控制

   • 电压PWM控制就是通过调节占空比来改变施加在电机上的平均电压。
     matlab
dutycycle = 0.5; % 初始占空比
     sampling time = 0.001; % 采样时间
t = 0:samplingtime:1; % 时间向量
     voltage = zeros(size(t));
     for i = 1:length(t)
     if mod(i,floor(1/duty cycle)) <= floor(dutycycle1/duty* cycle)
voltage(i)=Vmax; % V max为最大电压
else
voltage(i)=0;
end
end

   • 上面代码创建了一个时间向量，根据设定的占空比在不同时间点赋予电压值，实现PWM波形。改变占空比就能调整电机的平均电压，进而控制电机转速。

3. 角度位置控制

   • 角度位置控制主要是根据电机转子位置来控制开通和关断角度。
     matlab
rotorposition = get rotorposition(); % 获取转子位置，假设get rotorposition()是获取位置函数
     turn onangle = 10; % 开通角度
     turn offangle = 30; % 关断角度
     if rotor position >= turnon angle && rotorposition < turn offangle
     switch on();
else
switch_off();
end

   • 通过判断转子位置是否在设定的开通和关断角度区间内，决定开关的状态，以此来控制电机转矩。

（二）智能控制策略

1. 12/8三相开关磁阻电机有限元分析本体建模

   • 有限元分析本体建模能更精确地模拟电机的电磁特性。在Matlab中，可以借助一些专业的有限元分析工具箱。不过这块代码相对复杂，涉及到网格划分、材料属性设置等。
     matlab
% 简单示意设置材料属性
material = 'iron';
setmaterial property(material); % 假设setmaterial property()是设置材料属性函数

   • 材料属性设置好后，进行网格划分，不同的结构和精度要求会有不同的划分方式，这里就不详细展开代码了。

2. 转矩分配函数控制

   • 转矩分配函数控制（TDFC）是将总转矩合理分配到各相。
     matlab
totaltorque = get totaltorque(); % 获取总转矩
     torque perphase = zeros(3,1); % 三相转矩初始值
     for i = 1:3
     torque perphase(i)=total torque*tdf(i); % tdf是转矩分配函数值数组
end

   • 上述代码根据转矩分配函数值数组tdf，将总转矩分配到三相，使得电机转矩波动更小。

3. 模糊PID控制

   • 模糊PID控制结合了模糊控制的灵活性和PID控制的精确性。
     matlab
% 假设已经有模糊推理系统fis
error = geterror(); % 获取误差
     de = get d_error(); % 获取误差变化率
[kp,ki,kd]=evalfis([error,de],fis); % 根据模糊推理系统计算PID参数

   • 通过模糊推理系统fis，根据误差和误差变化率实时调整PID参数，提高系统的响应速度和稳定性。

4. 模糊角度控制

   • 模糊角度控制根据电机运行状态模糊调整开通和关断角度。
     matlab
% 假设已经有模糊推理系统fisangle
     speed = get speed(); % 获取电机速度
load = getload(); % 获取负载
     [on angle,offangle]=evalfis([speed,load],fis angle); % 根据模糊推理系统计算开通和关断角度

   • 利用模糊推理系统fis_angle，综合考虑速度和负载，动态调整角度，优化电机性能。

5. 神经网络在线自适应迭代控制

   • 神经网络在线自适应迭代控制利用神经网络强大的非线性映射能力来调整控制参数。
     matlab
net = feedforwardnet([10]); % 创建一个有10个隐藏层神经元的前馈神经网络
trainX = [errordata;de data]; % 误差和误差变化率数据作为输入
trainY = [kpdata;ki data;kddata]; % PID参数数据作为输出
     net = train(net,trainX,trainY); % 训练神经网络
     new error = getnew error(); % 获取新的误差
newde = get newd error(); % 获取新的误差变化率
[newkp,new ki,newkd]=net([new error;new_de]); % 根据训练好的网络计算新的PID参数

   • 先训练神经网络，然后根据新的误差和误差变化率实时计算新的PID参数，实现自适应控制。

（三）部分离线迭代算法

1. 遗传算法优化PID

   • 遗传算法（GA）可以在众多参数组合中找到较优的PID参数。
     matlab
% 定义适应度函数
function fitness = pidfitness(kp,ki,kd)
     % 假设已经有系统模型，根据kp,ki,kd计算系统响应，得出适应度值
     sys = tf([kpkd kp* ki kp],[1 0 0]);
     [y,t]=step(sys);
     fitness = sum(abs(y - desired* response)); % desiredresponse为期望响应
     end
     % 设置遗传算法参数
     nvars = 3; % 三个变量，kp,ki,kd
     lb = [0 0 0]; % 变量下限
     ub = [100 100 100]; % 变量上限
     options = gaoptimset('Generations',100,'PopulationSize',50);
     [x,fval] = ga(@(kp,ki,kd)pid fitness(kp,ki,kd),nvars,[],[],[],[],lb,ub,[],options);

   • 遗传算法通过不断迭代，寻找使适应度函数最优的PID参数组合，这里以系统响应与期望响应的误差绝对值和作为适应度函数。

2. 粒子群算法优化PID

   • 粒子群算法（PSO）也是一种优化算法，它模拟鸟群觅食行为。
     matlab
% 定义适应度函数同遗传算法
function fitness = pidfitness(kp,ki,kd)
     sys = tf([kpkd kp* ki kp],[1 0 0]);
     [y,t]=step(sys);
     fitness = sum(abs(y - desired* response));
end
% 设置粒子群算法参数
nvars = 3;
lb = [0 0 0];
ub = [100 100 100];
options = optimoptions('particleswarm','SwarmSize',50,'MaxIterations',100);
[x,fval] = particleswarm(@(kp,ki,kd)pid_fitness(kp,ki,kd),nvars,lb,ub,[],options);

   • 粒子群算法通过粒子在解空间的飞行，寻找最优解，同样以适应度函数来评估解的优劣。

这个开关磁阻电机控制仿真模型涵盖了多种控制策略和优化算法，在实际应用和研究中都很有价值，希望对大家有所帮助呀！