教材《概率论与随机过程》北京邮电大学出版社
适用于本科计算机专业
赌徒破产模型是一个完美的框架 ,几乎所有的核心概念都可以在这个模型里找到直观例子。
我们用这个模型为主线,把所有知识点串一遍。
一、主线:赌徒破产模型(基本设置)(or 随机游动,醉汉回家)
状态 :赌徒A当前的钱数 {0,1,2,...,n}
规则:每次赌博,以概率 p 赢1元,以概率 q=1−p输1元。
-
如果钱到 0,破产,游戏结束(吸收)。
-
如果钱到 n,赢够,游戏结束(吸收)。
-
在 1,2,...,n−1 之间持续游走。(暂态)
1、如果状态 ii 是吸收态(pii=1),则从 ii 出发下一步必然回到 ii,所以 首次返回概率 fii=1 → 是常返态。并且吸收态的平均返回时间 μi=1(如果从自身出发立即返回),所以是 正常返。
2、1 到 n-1 是暂态, 最终以概率 1 进入吸收态 0 或 n(有限步内),有可能在进入吸收态后永不回到中间态,所以 fii<1 → 暂态。暂态没有平均返回时间(因为平均返回时间 μi 的定义以常返为前提,即 fii=1 时才有意义)。
3、周期
-
对于吸收态 0:能回到 0 的步数集合是 {1,2,3,...},因为p00(1)=1,从 0 出发第 1 步、第 2 步...都仍在 0,gcd=1 → 周期为 1(非周期)。
-
对于吸收态 n:同理,周期 1。
-
对于中间状态 1,2,...,n−1:回到原点的步数必须是偶数(左右步数相等),所以步数集合是 {2,4,6,...} → gcd=2 → 周期为 2。
4、遍历性
遍历状态 = 正常返 + 非周期(周期1)(+ 互通类内所有状态满足此条件)。
赌徒模型中:
-
0,n:正常返 + 周期 1 → 遍历。
-
中间状态 1,...,n−1:暂态 → 不是遍历。
5、赌徒模型不是不可约
| 状态 | 常返/暂态 | 正常返/零常返(常返时才讨论) | 周期 | 遍历? |
|---|---|---|---|---|
| 0 | 常返 | 正常返 (μ=1) | 1 | 是 |
| n | 常返 | 正常返 (μ=1) | 1 | 是 |
| 1...n-1 | 暂态 | 不讨论 | 2 | 否 |
二、顺着主线:引入定义
1. 马氏性
P(Xn+1=j∣X0,...,Xn=i)=P(Xn+1=j∣Xn=i)
在赌徒模型中:下一局输赢(状态变化)只取决于当前钱数,与之前怎么赢/输无关 ------ 天然满足马氏性。
2. 齐次性
一步转移概率 pi,i+1=p,pi,i−1=q,与时间 n 无关 → 齐次链。
3. n步转移概率 pij(n)
从钱 i开始,经过 n 局后钱变为 j的概率。
C-K方程:
pij(m+n)=∑kpik(m)pkj(n)
矩阵形式:P(n)=P^n
在赌徒模型里:想算 n 步后钱的分布,就要算 Pn。
4. 有限维分布
初始分布 πi(0)=P(X0=i)
绝对分布 πj(n)=P(Xn=j)
公式:
π(n)=π(0)Pn
即 n 步后分布 = 初始分布 × n步转移矩阵。
在赌徒模型里:给定初始钱数i(即初始分布集中在 i),则 π(n) 就是 n 局后钱数的分布。
三、状态分类(这是重点)
1. 可达与互通
可达 i→j:存在 n 使 pij(n)>0。
互通 i↔j:互相可达。
赌徒模型中:
-
1↔2↔⋯↔n−1 (互通)
-
0 只到自身,n只到自身(吸收)
-
从 0 不能到其他状态(除了自身),所以 0 与中间状态不互通。
2. 常返 vs 暂态
常返 :从 i 出发,最终回到 i 的概率 fii=1 。
暂态:fii<1。
判断常返的另一个等价定理:
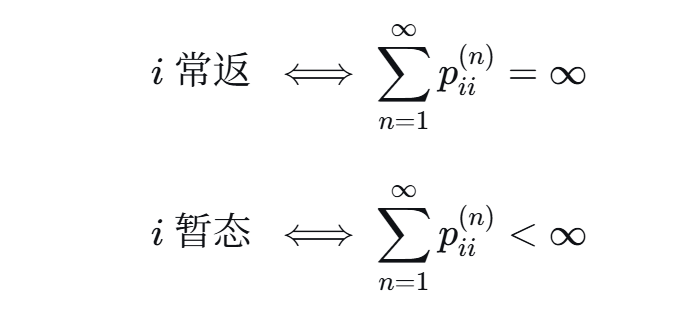
级数收敛 → 暂态。
3. 正常返 vs 零常返
常返时,定义 平均返回时间:

-
如果 μi<∞ → 正常返
-
如果 μi=∞ → 零常返(返回时间均值为无穷)
有限链定理:有限状态马氏链,没有零常返状态,常返必是正常返。
4. 周期
定义:状态 ii 的周期
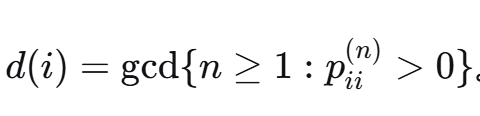
5. 遍历状态
正常返 + 非周期 → 遍历。
四、类性质
-
互通的状态 常返性相同、正常/零常返相同、周期相同。
-
赌徒模型中间互通类 {1,...,n−1} 都是暂态(有吸收可达,不闭)。
-
吸收态 {0},{n} 各自是闭集(出去概率为0)。
五、状态空间分解定理
状态空间 E= 非常返集 D ∪ 常返闭集 C1∪C2∪...
赌徒模型:
E={0}∪{n}∪{1,2,...,n−1}
-
{0},{n}:两个常返闭集(正常返,吸收)
-
{1,...,n−1}{1,...,n−1}:非常返集 D
满足:从 D 可进入常返闭集,但反过来不行。
六、平稳分布与极限分布
平稳分布 π=(π0,...,πn) 满足:
πP=π,∑πj=1
物理意义:如果初始分布是 π,那么任意时刻分布都是 π(不变)。
极限分布:
limn→∞pij(n)=πj(与i无关)
存在的条件:链不可约 + 遍历(所有状态正常返非周期)。
赌徒模型:
-
可约(因为有多个闭集),极限分布与初态有关:如果从中间出发,最终被 0 或 n 吸收的概率不同,极限分布可能是 (1,0,...,0) 或 (0,...,0,1),取决于初态。
-
平稳分布:有多个,因为每个吸收闭集上可定义一个平稳分布(集中在吸收态上)。方程 πP=ππP=π 的解不唯一。
七、解题与串联主线的方法
-
先画状态图,标转移概率。
-
判断互通、闭集。
-
判断常返/暂态:
-
吸收态 → 常返
-
有限状态非闭互通类 → 暂态(若有别的闭集可达)
-
利用定理:有限链常返态都是正常返。
-
-
周期:看回自身的步数集合的 gcd。
-
平稳分布:解 πP=π,看链结构:
-
多个闭集 → 多个平稳分布
-
不可约遍历 → 唯一平稳分布 = 极限分布
-
八、核心定理快速回顾

如果按这个主线------从赌徒模型出发,引入每个概念,再用模型解释 就不会乱。
做题时,先归类模型(是否有限、互通性、闭集),然后套用上面定理,不用每次都从定义硬算。