文章目录
- [1. 2ASK的基本原理](#1. 2ASK的基本原理)
- [2. 2ASK调制器](#2. 2ASK调制器)
-
- [2.1 模拟调制器(DSB-SC Modulator)](#2.1 模拟调制器(DSB-SC Modulator))
- [2.2 键控调制器(Keying Modulator)](#2.2 键控调制器(Keying Modulator))
- [3. 2ASK信号的波形与频谱](#3. 2ASK信号的波形与频谱)
- [4. 2ASK信号的解调](#4. 2ASK信号的解调)
-
- [4.1 AWGN信道下2ASK的最佳接收模型](#4.1 AWGN信道下2ASK的最佳接收模型)
- [4.2 2ASK误码性能分析](#4.2 2ASK误码性能分析)
- [4.3 OOK信号的非相干解调](#4.3 OOK信号的非相干解调)
1. 2ASK的基本原理
2ASK(binary amplitude shift keying,二进制幅移键控)核心原理是用二进制基带信号控制载波幅度的两种状态,这两种状态理论上可以是任意两个不同的幅度值(比如 A cos 2 π f c t A\cos 2\pi f_{\rm c} t Acos2πfct 和 0.5 A cos 2 π f c t 0.5A\cos 2\pi f_{\rm c} t 0.5Acos2πfct)。
OOK(on-off keying,通断键控)是2ASK的特例,它直接将载波的两种幅度状态定义为 "有载波"(对应数字"1")和"无载波"(对应数字"0") ,波形如图1所示,其数学表达式为:
s 2 A S K ( t ) = { A cos 2 π f c t , 传输 " 1 " 时 0 , 传输 " 0 " 时 s_{\rm 2ASK}(t)=\begin{cases}A\cos2\pi f_ct, & 传输"1"时 \\ 0, & 传输"0"时\end{cases} s2ASK(t)={Acos2πfct,0,传输"1"时传输"0"时其中, f c f_c fc为载波频率, A A A为载波幅度。
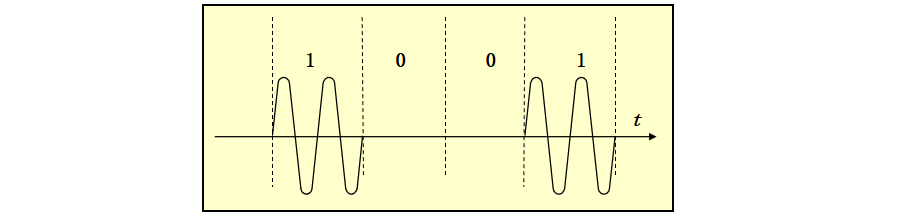
图1 OOK波形示意图
2. 2ASK调制器
图2给出了两种典型的2ASK调制器结构。
2.1 模拟调制器(DSB-SC Modulator)
- 结构:脉冲调制输出的基带信号 m ( t ) m(t) m(t),与载波 A cos 2 π f c t A\cos2\pi f_{\rm c}t Acos2πfct相乘。
- 原理:利用乘法器实现频谱搬移,将基带信号频谱搬移到 ± f c \pm f_{\rm c} ±fc处,类似于模拟调制中的DSB-SC调制,形成双边带信号。
2.2 键控调制器(Keying Modulator)
- 结构:通过数字基带信号控制开关电路,实现载波的"通/断"控制。
- 原理:传输"1"时开关闭合,载波输出;传输"0"时开关断开,无信号输出,本质是一种简单的振幅键控方式(OOK)。
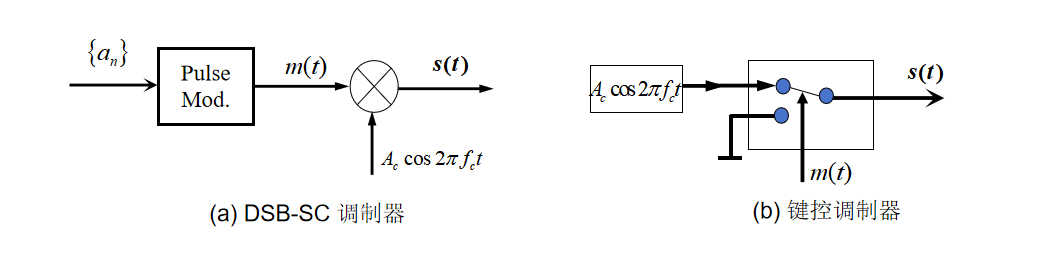
图2 2ASK调制器
3. 2ASK信号的波形与频谱
根据基带脉冲的带宽特性,2ASK信号分为两种类型。
3.1 无限带宽2ASK信号:发送信号的基带脉冲为方波
(1)波形特征
图3(a)为基带信号 m ( t ) m(t) m(t)波形,它是二进制不归零矩形脉冲序列,而矩形脉冲的频谱是无限带宽 的。 m ( t ) m(t) m(t)经过图3(b)的调制器,与载波 A c cos 2 π f c t A_c\cos2\pi f_c t Accos2πfct相乘,就得到无限带宽的2ASK信号 s ( t ) s(t) s(t),显然它频谱也会继承"无限带宽"的特性。由于它是随机信号,因此我们下面将分析它的功率谱特性。
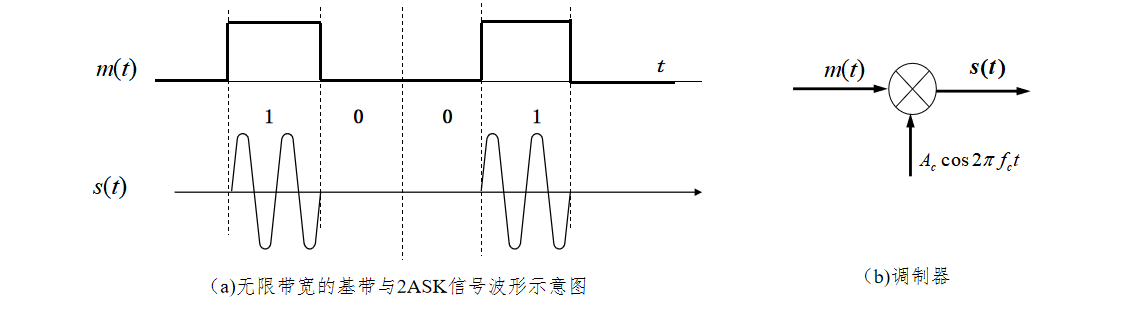
图3 无限带宽2ASK信号的波形
(2)功率谱密度
在深入分析2ASK信号功率谱密度之前,我们先回顾一个随机信号的性质。
如图3(b)所示的"随机信号×余弦载波"的调制过程,即
s ( t ) = m ( t ) ⋅ cos 2 π f c t s(t)=m(t)\cdot\cos2\pi f_ct s(t)=m(t)⋅cos2πfct输出信号 s ( t ) s(t) s(t)的功率谱为
P S ( f ) = 1 4 [ P M ( f − f c ) + P M ( f + f c ) ] (1) \tag{1} P_S(f)=\frac{1}{4}\left[P_M(f-f_c)+P_M(f+f_c)\right] PS(f)=41[PM(f−fc)+PM(f+fc)](1)也就是说,2ASK信号 s ( t ) s(t) s(t)的功率谱密度 P S ( f ) P_S(f) PS(f),是基带信号 m ( t ) m(t) m(t)的功率谱 P M ( f ) P_M(f) PM(f)分别向 f c f_c fc和 − f c -f_c −fc"处搬移,并乘以系数 1 4 \frac{1}{4} 41后的结果。
显然,我们首先需要求出基带信号 m ( t ) m(t) m(t)的功率谱密度 P M ( f ) P_M(f) PM(f)。由于基带信号 m ( t ) m(t) m(t)为0、1等概的二进制不归零矩形脉冲序列,其功率谱求解如下。
- 步骤1:明确单极性不归零脉冲的基础参数
单极性不归零矩形脉冲的基带信号 m ( t ) m(t) m(t)是由"0""1"电平的矩形脉冲组成的随机序列:
- 脉冲波形: g T ( t ) = A Rect ( t T s ) g_T(t) = A\text{Rect}\left( \frac{t}{T_{\rm s}} \right) gT(t)=ARect(Tst)( T s T_{\rm s} Ts是码元宽度, A A A是脉冲幅度, Rect ( ⋅ ) \text{Rect}(\cdot) Rect(⋅)是矩形窗函数);
- 傅里叶变换: G T ( f ) = A T s Sa ( π f T s ) G_{\rm T}(f) = A T_{\rm s} \text{Sa}(\pi f T_{\rm s}) GT(f)=ATsSa(πfTs)( Sa ( x ) = sin x x \text{Sa}(x)=\frac{\sin x}{x} Sa(x)=xsinx是抽样函数);
- 统计特性(0、1等概率):假设 A = 1 A=1 A=1,则有均值 m a = 1 2 m_a = \frac{1}{2} ma=21,方差 σ a 2 = 1 4 \sigma_a^2 = \frac{1}{4} σa2=41
- 步骤2:代入随机脉冲序列的功率谱公式,包含连续谱+离散谱 两部分
P M ( f ) = σ a 2 T s ∣ G T ( f ) ∣ 2 + m a 2 T s ∑ k = − ∞ ∞ ∣ G T ( k T s ) ∣ 2 δ ( f − k T s ) (2) \tag{2} P_M(f) = \frac{\sigma_a^2}{T_{\rm s}} \left| G_{\rm T}(f) \right|^2 + \frac{m_a^2}{T_{\rm s}} \sum_{k=-\infty}^{\infty} \left| G_{\rm T}\left( \frac{k}{T_{\rm s}} \right) \right|^2 \delta\left( f - \frac{k}{T_{\rm s}} \right) PM(f)=Tsσa2∣GT(f)∣2+Tsma2k=−∞∑∞ GT(Tsk) 2δ(f−Tsk)(2)- 步骤3:代入参数并化简
- 连续谱
σ a 2 T s ∣ G T ( f ) ∣ 2 = A 2 T s 4 Sa 2 ( π f T s ) \frac{\sigma_a^2}{T_{\rm s}} \left| G_{\rm T}(f) \right|^2 = \frac{A^2 T_{\rm s}}{4} \text{Sa}^2(\pi f T_{\rm s}) Tsσa2∣GT(f)∣2=4A2TsSa2(πfTs)- 离散谱
由于 G T ( k T s ) = A T s Sa ( π ⋅ k T s ⋅ T s ) = A T s Sa ( k π ) G_{\rm T}\left( \frac{k}{T_{\rm s}} \right) = A T_{\rm s} \text{Sa}\left( \pi \cdot \frac{k}{T_{\rm s}} \cdot T_{\rm s} \right) = A T_{\rm s} \text{Sa}(k\pi) GT(Tsk)=ATsSa(π⋅Tsk⋅Ts)=ATsSa(kπ)
而 Sa ( k π ) = sin ( k π ) k π \text{Sa}(k\pi) = \frac{\sin(k\pi)}{k\pi} Sa(kπ)=kπsin(kπ),仅当 k = 0 k=0 k=0时 Sa ( 0 ) = 1 \text{Sa}(0)=1 Sa(0)=1, k ≠ 0 k\neq0 k=0时 Sa ( k π ) = 0 \text{Sa}(k\pi)=0 Sa(kπ)=0。因此离散谱仅保留 k = 0 k=0 k=0项。
最终,0、1等概率下单极性不归零矩形脉冲序列的功率谱密度为:
P M ( f ) = A 2 T s 4 Sa 2 ( π f T s ) + A 2 4 δ ( f ) (3) \tag{3} P_M(f) = \frac{A^2 T_{\rm s}}{4} \text{Sa}^2(\pi f T_{\rm s}) + \frac{A^2}{4} \delta(f) PM(f)=4A2TsSa2(πfTs)+4A2δ(f)(3)
综合公式(1)(2),可以得到
P 2 A S K ( f ) = A 2 T s 4 [ S a 2 ( π ( f − f c ) T s ) + S a 2 ( π ( f + f c ) T s ) ] + A 2 4 δ ( f − f c ) + A 2 4 δ ( f + f c ) (4) \tag{4} P_{\rm 2ASK}(f)=\frac{A^2T_{\rm s}}{4}\left[{\rm Sa}^2\left(\pi(f-f_{\rm c})T_{\rm s}\right)+Sa^2\left(\pi(f+f_{\rm c})T_{\rm s}\right)\right]+\frac{A^2}{4}\delta(f-f_{\rm c})+\frac{A^2}{4}\delta(f+f_{\rm c}) P2ASK(f)=4A2Ts[Sa2(π(f−fc)Ts)+Sa2(π(f+fc)Ts)]+4A2δ(f−fc)+4A2δ(f+fc)(4)
图4为基带以及频带2ASK信号功率谱密度,从图4(b)可以看到:
- ASK功率谱是基带谱向 ± f c \pm f_c ±fc处搬移的结果,在 f = f c f = f_c f=fc和 f = − f c f = -f_c f=−fc附近形成两个对称的谱瓣;
- 2ASK信号为无限带宽信号,取其主要能量的集中区间,可以得到第一过零点带宽 B = 2 r s B=2r_{\rm s} B=2rs,是基带第一过零点带宽的2倍。
- 在 ± f c \pm f_{\rm c} ±fc处有两个离散冲激,这是由于基带信号为单极性信号带来的。
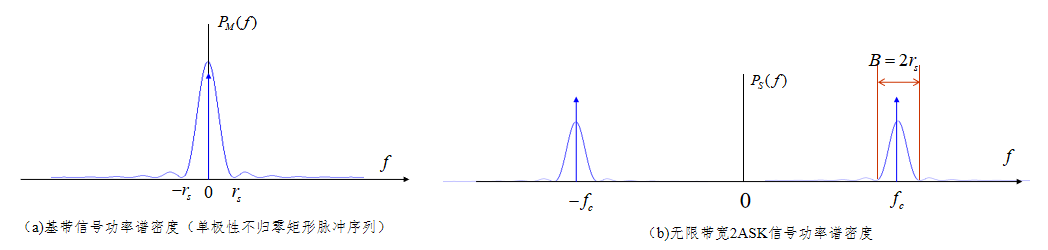
图4 无限带宽2ASK信号功率谱密度
3.2 有限带宽2ASK信号:发送信号的基带脉冲为根升余弦波形
(1)波形特征
图5中 m ( t ) m(t) m(t)为带宽有限 的基带信号波形,它是二进制根升余弦脉冲序列。 m ( t ) m(t) m(t)经过图3(b)的调制器,与载波 A c cos 2 π f c t A_c\cos2\pi f_c t Accos2πfct相乘,就得到带宽有限的2ASK信号 s ( t ) s(t) s(t),下面通过功率谱特性,我们来分析信号带宽。
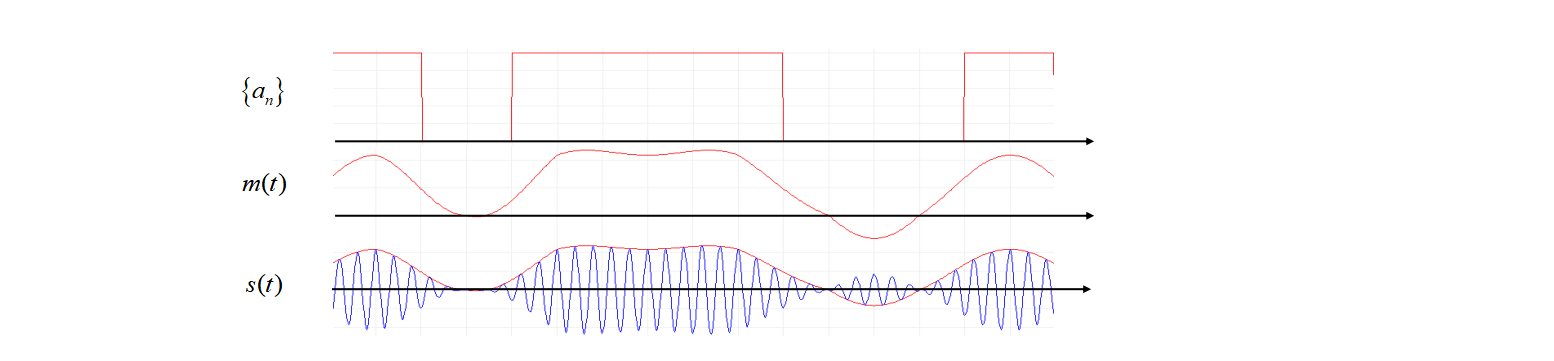
图5 有限带宽2ASK信号波形示意图
(2)功率谱密度
同样基于公式(1),可以得到带宽有限的2ASK信号功率谱密度,即
P 2 A S K ( f ) = 1 4 [ P M ( f − f c ) + P M ( f + f c ) ] P_{\rm 2ASK}(f)=\frac{1}{4}\left[P_M(f-f_c)+P_M(f+f_c)\right] P2ASK(f)=41[PM(f−fc)+PM(f+fc)]其中, P M ( f ) P_M(f) PM(f)为基带脉冲的功率谱密度(升余弦频谱),重写公式(2)
P M ( f ) = σ a 2 T s ∣ G T ( f ) ∣ 2 + m a 2 T s ∑ k = − ∞ ∞ ∣ G T ( k T s ) ∣ 2 δ ( f − k T s ) P_M(f) = \frac{\sigma_a^2}{T_{\rm s}} \left| G_{\rm T}(f) \right|^2 + \frac{m_a^2}{T_{\rm s}} \sum_{k=-\infty}^{\infty} \left| G_{\rm T}\left( \frac{k}{T_{\rm s}} \right) \right|^2 \delta\left( f - \frac{k}{T_{\rm s}} \right) PM(f)=Tsσa2∣GT(f)∣2+Tsma2k=−∞∑∞ GT(Tsk) 2δ(f−Tsk)由于采用根升余弦波形,显然 ∣ G T ( f ) ∣ 2 = ∣ H R C ( f ) ∣ |G_{\rm T}(f)|^2=|H_{\rm RC}(f)| ∣GT(f)∣2=∣HRC(f)∣,且均值 m a = 1 2 m_a = \frac{1}{2} ma=21,方差 σ a 2 = 1 4 \sigma_a^2 = \frac{1}{4} σa2=41,因此
P M ( f ) = 1 4 T s ∣ H R C ( f ) ∣ + 1 4 δ ( 0 ) (5) \tag{5} P_M(f) =\frac{1}{4T_{\rm s}}|H_{\rm RC}(f)|+\frac{1}{4}\delta(0) PM(f)=4Ts1∣HRC(f)∣+41δ(0)(5)
注:升余弦滤波器的频率传递函数如下
H R C ( f ) = { T s , ∣ f ∣ < 1 2 T s ( 1 − α ) T s 2 { 1 − sin [ T s α ( f − 1 2 T s ) ] } , 1 2 T s ( 1 − α ) ≤ ∣ f ∣ ≤ 1 2 T s ( 1 + α ) 0 , ∣ f ∣ > 1 2 T s ( 1 + α ) (5b) \tag{5b} H_{\rm RC}(f)= \begin{cases} T_s, & |f| < \dfrac{1}{2T_s}(1-\alpha) \\ \dfrac{T_s}{2}\left\{1-\sin\left[\dfrac{T_s}{\alpha}\left(f - \dfrac{1}{2T_s}\right)\right]\right\}, & \dfrac{1}{2T_s}(1-\alpha) \leq |f| \leq \dfrac{1}{2T_s}(1+\alpha) \\ 0, & |f| > \dfrac{1}{2T_s}(1+\alpha) \end{cases} HRC(f)=⎩ ⎨ ⎧Ts,2Ts{1−sin[αTs(f−2Ts1)]},0,∣f∣<2Ts1(1−α)2Ts1(1−α)≤∣f∣≤2Ts1(1+α)∣f∣>2Ts1(1+α)(5b)
故有限带宽2ASK的功率谱密度为
P 2 A S K ( f ) = 1 4 T s [ ∣ H R C ( f − f c ) ∣ + ∣ H R C ( f + f c ) ∣ ] + 1 4 δ ( f − f c ) + A 2 4 δ ( f + f c ) , (6) \tag{6} P_{\rm 2ASK}(f)=\frac{1}{4T_{\rm s}}\left[|H_{\rm RC}(f-f_{\rm c})|+|H_{\rm RC}(f+f_{\rm c})|\right]+\frac{1}{4}\delta(f-f_{\rm c})+\frac{A^2}{4}\delta(f+f_{\rm c}), P2ASK(f)=4Ts1[∣HRC(f−fc)∣+∣HRC(f+fc)∣]+41δ(f−fc)+4A2δ(f+fc),(6)其示意图如图6所示,其特点在于
- 2ASK信号带宽 B = ( 1 + α ) r s B=(1+\alpha)r_s B=(1+α)rs,是基带信号带宽两倍;
- 在 ± f c \pm f_{\rm c} ±fc处有两个离散冲激,这是由于基带信号为单极性信号带来的。
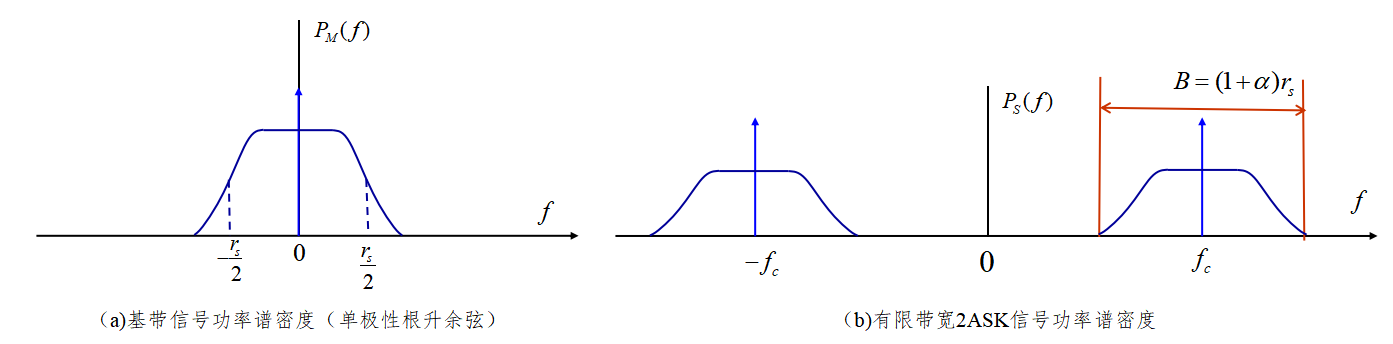
图6 有限带宽2ASK信号功率谱密度
4. 2ASK信号的解调
解调是调制的逆过程,核心是从频带信号中恢复出原始数字基带信号。2ASK信号的解调分为相干解调和非相干解调两类。
4.1 AWGN信道下2ASK的最佳接收模型
图7展示的是2ASK信号的相关接收机解调过程。其中, s 2 A S K ( t ) s_{\rm 2ASK}(t) s2ASK(t)为经过信道传输的2ASK信号,
s 2 A S K ( t ) = { s 1 ( t ) , "1" s 2 ( t ) , "0" , 0 ≤ t < T s (7) \tag{7} s_{\rm 2ASK}(t)= \begin{cases} s_1(t) , & \text{"1"} \\ s_2(t), & \text{"0"} \end{cases},\quad0\le t<T_{\rm s} s2ASK(t)={s1(t),s2(t),"1""0",0≤t<Ts(7)信号在进入接收机之前,叠加单边功率谱密度为 N 0 N_0 N0的AWGN噪声 n w ( t ) n_w(t) nw(t),得到接收信号
r ( t ) = s 2 A S K ( t ) + n w ( t ) . (8) \tag{8} r(t)=s_{\rm 2ASK}(t)+n_w(t). r(t)=s2ASK(t)+nw(t).(8)接收信号 r ( t ) r(t) r(t)与本地参考信号 s 1 ( t ) s_1(t) s1(t)相乘后,通过积分器完成一个码元周期 T s T_{\rm s} Ts内的积分并在 t = T s t=T_{\rm s} t=Ts抽样(该过程实现了"匹配滤波"的等效运算),得到判决变量
y = ∫ 0 T s [ s i ( t ) + n w ( t ) ] s 1 ( t ) d t , i = 1 , 2. (9) \tag{9} y= \int_{0}^{T_{\rm s}} \left[ s_i(t) + n_w(t) \right] s_1(t) dt,\quad i=1,2. y=∫0Ts[si(t)+nw(t)]s1(t)dt,i=1,2.(9)再通过判决(与阈值比较),还原出原始二进制序列的估计值 b ^ n \hat{b}_n b^n。
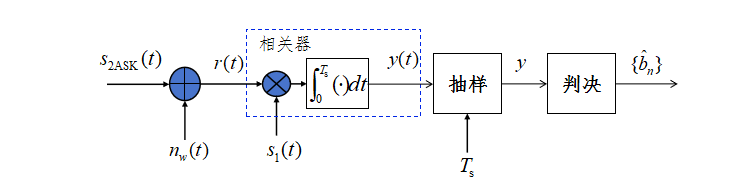
图7 2ASK信号相关接收机模型
4.2 2ASK误码性能分析
下面我们分析误码率。显然,根据(7)(8),我们有
- 发送"1"时,接收信号 r ( t ) = s 1 ( t ) + n w ( t ) r(t)=s_1(t)+n_w(t) r(t)=s1(t)+nw(t),由此可以得到抽样时刻 t = T s t=T_s t=Ts的输出为:
y = ∫ 0 T s s 1 2 ( t ) d t + ∫ 0 T s s 1 ( t ) n w ( t ) d t = E s 1 + z (10) \tag{10} y=\int_0^{T_{\rm s}}s^2_1(t)dt+\int_0^{T_{\rm s}}s_1(t)n_w(t)dt=E_{\rm s1}+z y=∫0Tss12(t)dt+∫0Tss1(t)nw(t)dt=Es1+z(10)其中, E s 1 E_{\rm s1} Es1为 s 1 ( t ) s_1(t) s1(t)的符号能量, z z z为噪声分量,满足分布 z ∼ N ( 0 , E s 1 N 0 2 ) z\sim\mathcal{N}(0,\frac{E_{\rm s1}N_0}{2}) z∼N(0,2Es1N0)。 - 发送"0"时,接收信号 r ( t ) = s 2 ( t ) + n w ( t ) r(t)=s_2(t)+n_w(t) r(t)=s2(t)+nw(t),由此可以得到抽样时刻 t = T s t=T_s t=Ts的输出为:
y = ∫ 0 T s s 1 ( t ) s 2 ( t ) d t + ∫ 0 T s s 1 ( t ) n w ( t ) d t = ∫ 0 T s s 1 ( t ) s 2 ( t ) d t + z , y=\int_0^{T_{\rm s}}s_1(t)s_2(t)dt+\int_0^{T_{\rm s}}s_1(t)n_w(t)dt=\int_0^{T_{\rm s}}s_1(t)s_2(t)dt+z, y=∫0Tss1(t)s2(t)dt+∫0Tss1(t)nw(t)dt=∫0Tss1(t)s2(t)dt+z,同样 z ∼ N ( 0 , E s 1 N 0 2 ) z\sim\mathcal{N}(0,\frac{E_{\rm s1}N_0}{2}) z∼N(0,2Es1N0)。基于图3和图5,我们假定 s 2 ( t ) = 0 s_2(t)=0 s2(t)=0,因此有
y = z . (11) \tag{11} y=z. y=z.(11)
基于(10)(11),可以得到判决变量 y y y在发送"1"和"0"时的条件概率密度函数 p ( y ∣ " 1 " ) p(y|"1") p(y∣"1")与 p ( y ∣ " 0 " ) p(y|"0") p(y∣"0")分别如图8中绿色和紫色分布所示。考虑"0""1"等概,设判决门限 V T = E s 1 / 2 V_{\rm T}=E_{\rm s1}/2 VT=Es1/2,此时误码率 P e = Q ( E s 1 2 N 0 ) P_{\rm e}=Q\left(\sqrt{\frac{E_{\rm s1}}{2N_0}}\right) Pe=Q(2N0Es1 )。由于平均符号能量 E s = 1 2 E s 1 E_{\rm s}=\frac{1}{2}E_{\rm s1} Es=21Es1,因此有
P e = Q ( E s N 0 ) (12) \tag{12} P_{\rm e}=Q\left(\sqrt{\frac{E_{\rm s}}{N_0}}\right) Pe=Q(N0Es )(12)
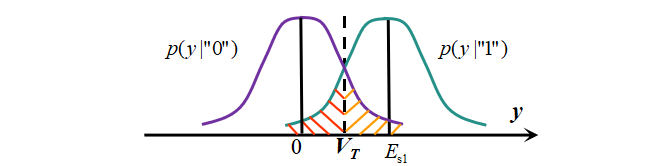
图8 分别发"1"和"0"时的条件概率密度函数 细心的读者可能已经注意到,我们在分析误码率的时候,并没有区分是频带有限的2ASK还是频带无限的2ASK信号,这是因为二者的接收机模型和误码率分析过程是一样的,不同的只是波形 s 1 ( t ) s_1(t) s1(t),即
- 带宽无限的2ASK信号, s 1 ( t ) s_1(t) s1(t)波形如图9(a)所示,显然有 E s 1 = A 2 2 T s E_{\rm s1}=\frac{A^2}{2}T_{\rm s} Es1=2A2Ts。
- 带宽有限的2ASK信号, s 1 ( t ) s_1(t) s1(t)波形如图9(b)所示,它的能量求解稍微复杂一点。推导如下:
根据帕塞瓦尔定理,有
E s 1 = ∫ − ∞ ∞ ∣ s 1 ( t ) ∣ 2 d t = ∫ − ∞ ∞ ∣ S 1 ( f ) ∣ 2 d f E_{\rm s1}=\int_{-\infty}^{\infty}|s_1(t)|^2 dt = \int_{-\infty}^{\infty}|S_1(f)|^2 df Es1=∫−∞∞∣s1(t)∣2dt=∫−∞∞∣S1(f)∣2df图9(b)中的波形 s 1 ( t ) = A c m 1 ( t ) cos 2 π f c t s_1(t)=A_{\rm c}m_1(t)\cos2\pi f_{\rm c}t s1(t)=Acm1(t)cos2πfct,模型如图9( c) 所示,显然有 S 1 ( f ) = A c 2 [ M 1 ( f − f c ) + M 1 ( f + f c ) ] S_1(f)=\frac{A_{\rm c}}{2}[M_1(f-f_{\rm c})+M_1(f+f_{\rm c})] S1(f)=2Ac[M1(f−fc)+M1(f+fc)],其中 ∣ M 1 ( f ) ∣ = H R C ( f ) |M_1(f)|=\sqrt{H_{\rm RC}(f)} ∣M1(f)∣=HRC(f) ,故 E s 1 = A c 2 4 ∫ − ∞ ∞ [ H R C ( f − f c ) + H R C ( f + f c ] d f = A c 2 2 E_{\rm s1}=\frac{A_{\rm c}^2}{4}\int_{-\infty}^{\infty}[H_{\rm RC}(f-f_{\rm c})+H_{\rm RC}(f+f_{\rm c}] df=\frac{A_{\rm c}^2}{2} Es1=4Ac2∫−∞∞[HRC(f−fc)+HRC(f+fc]df=2Ac2。
图9
4.3 OOK信号的非相干解调
非相干解调无需恢复载波相位,结构简单,成本低,适用于对误码率要求不高的场景,如图10所示,由带通滤波器(BPF)、整流器(Rectifier)、低通滤波器(LPF)、抽样和比较器组成。
我这就拆解这个OOK解调流程里每个模块的具体功能:
- 带通滤波器(BPF):从输入的 s OOK ( t ) s_{\text{OOK}}(t) sOOK(t) 中筛选出OOK信号对应的载波频段,滤除其他频段的噪声、干扰信号。
- 整流器:把BPF输出的"正负波动的交流信号"(载波信号)转换成单极性信号(只保留正极性),相当于提取信号的"包络轮廓"。
- 低通滤波器(LPF):过滤掉整流后信号里的高频载波成分,只保留基带信号的包络(也就是OOK对应的0/1信息)。
- 抽样模块:按照符号周期 T s T_s Ts(每个0/1符号的时长),在每个符号的结束时刻"抓取"LPF输出信号的幅度值。
- 判决模块:根据抽样得到的幅度值,判断当前符号是"1"还是"0":
在大信噪比条件下,OOK非相干解调的误码率近似为
P e ≈ 1 2 exp ( − E b 2 N 0 ) P_e \approx \frac{1}{2} \exp\left( -\frac{E_b}{2N_0} \right) Pe≈21exp(−2N0Eb)相比相干解调,非相干解调的误码性能略差,但无需载波同步电路,实现简单。
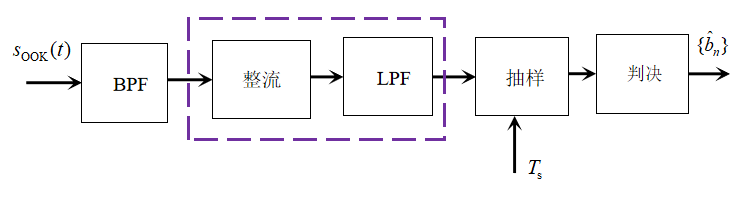
图10 OOK非相干解调器