脚本包含傅里叶变换和短时傅里叶分析功能: 傅里叶变换: 傅里叶变换是一种将时域信号转换到频域的方法。 它将一个连续或离散的信号分解成一系列复数频谱分量,表示信号在不同频率上的振幅和相位信息。 傅里叶变换适用于处理全局频谱特性比较稳定的信号,能够提供信号的完整频谱信息,但无法捕捉到信号随时间变化的动态特性。 短时傅里叶变换: 短时傅里叶变换是一种在时间上对信号进行分段处理并应用傅里叶变换的方法。 它将信号分成多个短时窗口,这个加窗处理也叫分帧,并对每个窗口应用傅里叶变换,得到相应的频谱信息。 通过在时间上移动窗口,可以获取信号在不同时间的频谱特性。 短时傅里叶变换适合处理频谱随时间变化的非平稳信号,可以提供信号的时间频率分布信息,但会损失一部分频谱分辨率和时间分辨率。
在信号处理的奇妙世界里,傅里叶变换(Fourier Transform)和短时傅里叶变换(Short - Time Fourier Transform,STFT)就像两把神奇的钥匙,帮助我们打开信号在频域和时频域的大门。今天,咱们就深入聊聊包含这两种强大功能的脚本。
傅里叶变换:窥探全局频谱的神器
傅里叶变换是个啥呢?简单来说,它就是一种能把时域信号华丽变身为频域信号的方法。想象一下,你有一个随时间变化的信号,可能是一段声音,或者是电路中的电压变化。傅里叶变换能把这个连续或离散的信号,拆解成一系列复数频谱分量,这些分量就像是信号在不同频率上的"积木",它们的振幅和相位信息,完整地描绘了信号在频域的样子。
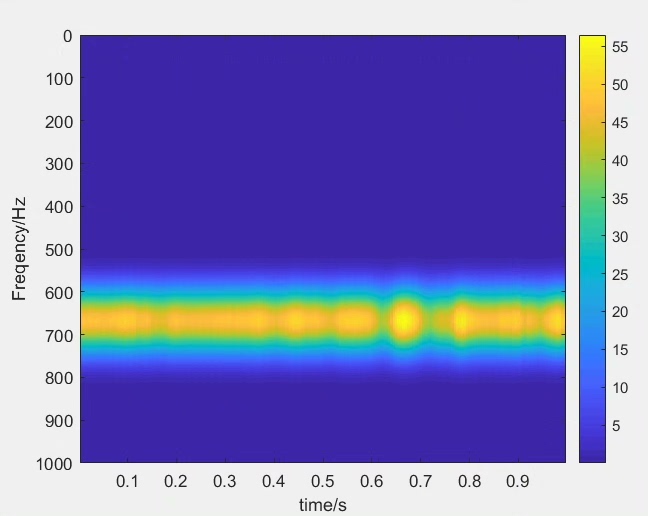
傅里叶变换特别适合那些全局频谱特性比较稳定的信号。比如说,一个持续稳定的正弦波信号,用傅里叶变换就能清晰地展示出它在单一频率上的能量分布。但它也有个小"缺点",就是对于信号随时间变化的动态特性,它有点"力不从心",没办法捕捉到。
下面咱们来点代码感受一下傅里叶变换的魅力,以Python为例,借助numpy和matplotlib库:
python
import numpy as np
import matplotlib.pyplot as plt
# 生成一个简单的时域信号,这里是频率为5Hz的正弦波
fs = 100 # 采样频率
t = np.linspace(0, 1, fs, endpoint=False) # 时间向量
y = np.sin(2 * np.pi * 5 * t) # 5Hz的正弦波
# 进行傅里叶变换
Y = np.fft.fft(y)
freq = np.fft.fftfreq(len(Y), 1/fs)
# 绘制时域图
plt.figure(figsize=(12, 6))
plt.subplot(2, 1, 1)
plt.plot(t, y)
plt.title('Time Domain Signal')
plt.xlabel('Time (s)')
plt.ylabel('Amplitude')
# 绘制频域图
plt.subplot(2, 1, 2)
plt.plot(freq[:fs//2], 2/fs * np.abs(Y[:fs//2]))
plt.title('Frequency Domain Signal')
plt.xlabel('Frequency (Hz)')
plt.ylabel('Magnitude')
plt.show()代码分析:
- 首先,我们定义了采样频率
fs和时间向量t,生成了一个频率为5Hz的正弦波y。这个正弦波就是我们要处理的时域信号。 - 接着,使用
np.fft.fft函数对y进行傅里叶变换,得到频域的复数结果Y。同时,通过np.fft.fftfreq计算出对应的频率向量freq。 - 绘图部分,我们用
plt.subplot创建了两个子图,分别绘制时域和频域的图像。在频域图中,由于傅里叶变换结果的对称性,我们只取前半部分进行绘制,并根据傅里叶变换的性质,对幅值进行了归一化处理(2/fs * np.abs(Y[:fs//2])),这样就能清晰地看到信号在频域的能量分布,在5Hz处会出现一个峰值,对应我们生成的正弦波频率。
短时傅里叶变换:捕捉动态频谱变化的能手
短时傅里叶变换则是为了解决傅里叶变换无法捕捉信号动态特性的问题而诞生的。它的思路很巧妙,就是在时间上对信号进行分段处理,然后对每一段分别应用傅里叶变换。具体做法就是把信号分成多个短时窗口,这个过程也叫加窗或者分帧。对每个窗口里的信号应用傅里叶变换,就能得到相应的频谱信息。通过在时间上移动这个窗口,我们就能获取信号在不同时间的频谱特性。
短时傅里叶变换特别适合处理那些频谱随时间变化的非平稳信号,比如一段音乐,不同时刻有不同的音符和节奏,它就能很好地展现出这些动态变化。不过呢,它也不是完美无缺,会在一定程度上损失频谱分辨率和时间分辨率。
同样用Python代码来体验短时傅里叶变换,这次我们借助 scipy.signal 库:
python
import numpy as np
import matplotlib.pyplot as plt
from scipy.signal import stft
# 生成一个频率随时间变化的信号
fs = 1000 # 采样频率
t = np.linspace(0, 1, fs, endpoint=False)
y = np.sin(2 * np.pi * 100 * t) + np.sin(2 * np.pi * 200 * (t - 0.5) * (t >= 0.5))
# 进行短时傅里叶变换
f, t_stft, Zxx = stft(y, fs=fs, window='hann', nperseg=128, noverlap=120)
# 绘制时频图
plt.figure(figsize=(12, 6))
plt.pcolormesh(t_stft, f, np.abs(Zxx), shading='gouraud')
plt.title('Short - Time Fourier Transform')
plt.ylabel('Frequency [Hz]')
plt.xlabel('Time [sec]')
plt.colorbar(label='Magnitude')
plt.show()代码分析:
- 这里我们生成了一个稍微复杂点的信号
y,前半段是100Hz的正弦波,后半段从0.5秒开始叠加了一个200Hz的正弦波,模拟频率随时间变化的非平稳信号。 - 使用
stft函数进行短时傅里叶变换。其中,window='hann'指定了汉宁窗,nperseg=128表示每个窗口包含128个采样点,noverlap=120表示相邻窗口有120个采样点重叠,这样可以提高时频分辨率。函数返回频率向量f、时间向量t_stft和短时傅里叶变换结果Zxx。 - 绘图部分,通过
plt.pcolormesh绘制时频图,用颜色表示信号在不同时间和频率上的幅值大小。从图中我们就能直观地看到信号频率随时间的变化情况,前半段主要能量集中在100Hz,后半段100Hz和200Hz都有能量分布。
傅里叶变换和短时傅里叶变换在信号处理中各有千秋,通过理解它们的原理并在脚本中实现,我们能更好地分析和处理各种信号,无论是音频、图像还是其他领域的信号。希望今天的分享能让你对这两种变换有更深入的理解和认识!