一种房间冲激响应测量方法

本文介绍了一种房间冲激响应测量方法。如有表述不当之处欢迎批评指正。欢迎任何形式的转载，但请务必注明出处。

1. 引言

房间冲激响应（Room Impulse Response, RIR）反应了房间的声学特性。在基于 AI 的音频应用中，RIR 主要用来做数据增强，即将高质量的干净音频信号与 RIR 进行卷积，来模拟在真实的房间/车载环境中，麦克风所采集的音频信号。

本文介绍了一种经典的房间冲激响应测量方法，该方法使用指数正弦扫频（Exponential Sine Sweep, ESS）信号作为激励信号，来进行测量。

2. 原理

x ( n ) ∗ h ( n ) = y ( n ) \begin{align} x(n) * h(n) = y(n) \end{align} x(n)∗h(n)=y(n)

公式 ( 1 ) (1) (1) 描述了声音传播的信号模型，即扬声器播放的信号 x ( n ) x(n) x(n) 经过房间的传播后（即与房间冲激响应 h ( n ) h(n) h(n) 卷积），被麦克风采集得到信号 y ( n ) y(n) y(n)。

如果能找到合适的 x ( n ) x(n) x(n)，满足：
x − 1 ( n ) ∗ x ( n ) = δ ( n ) \begin{align} x^{-1}(n) * x(n) = \delta(n) \end{align} x−1(n)∗x(n)=δ(n)

其中 δ ( n ) \delta(n) δ(n) 是冲激信号：
δ ( n ) = { 1 , n = 0 0 , n ≠ 0 \begin{align} \delta(n) = \begin{cases} 1, & n = 0 \\ 0, & n \neq 0 \end{cases} \end{align} δ(n)={1,0,n=0n=0

那么给公式 ( 1 ) (1) (1) 的左右两边同时卷积 x − 1 ( n ) x^{-1}(n) x−1(n)，可得：
x − 1 ( n ) ∗ x ( n ) ∗ h ( n ) = x − 1 ( n ) ∗ y ( n ) δ ( n ) ∗ h ( n ) = x − 1 ( n ) ∗ y ( n ) h ( n ) = x − 1 ( n ) ∗ y ( n ) \begin{align} x^{-1}(n) * x(n) * h(n) &= x^{-1}(n) * y(n) \notag \\ \delta(n) * h(n) &= x^{-1}(n) * y(n) \notag \\ h(n) &= x^{-1}(n) * y(n) \end{align} x−1(n)∗x(n)∗h(n)δ(n)∗h(n)h(n)=x−1(n)∗y(n)=x−1(n)∗y(n)=x−1(n)∗y(n)

现在的问题转换成什么信号适合做这个 x ( n ) x(n) x(n)。有研究人员提出可以使用 ESS 信号作为 x ( n ) x(n) x(n)。

3. ESS 信号及其卷积逆信号

ESS 信号的全称为 Exponential Sine Sweep，即指数正弦扫频信号，它有时也被称为对数扫频信号。

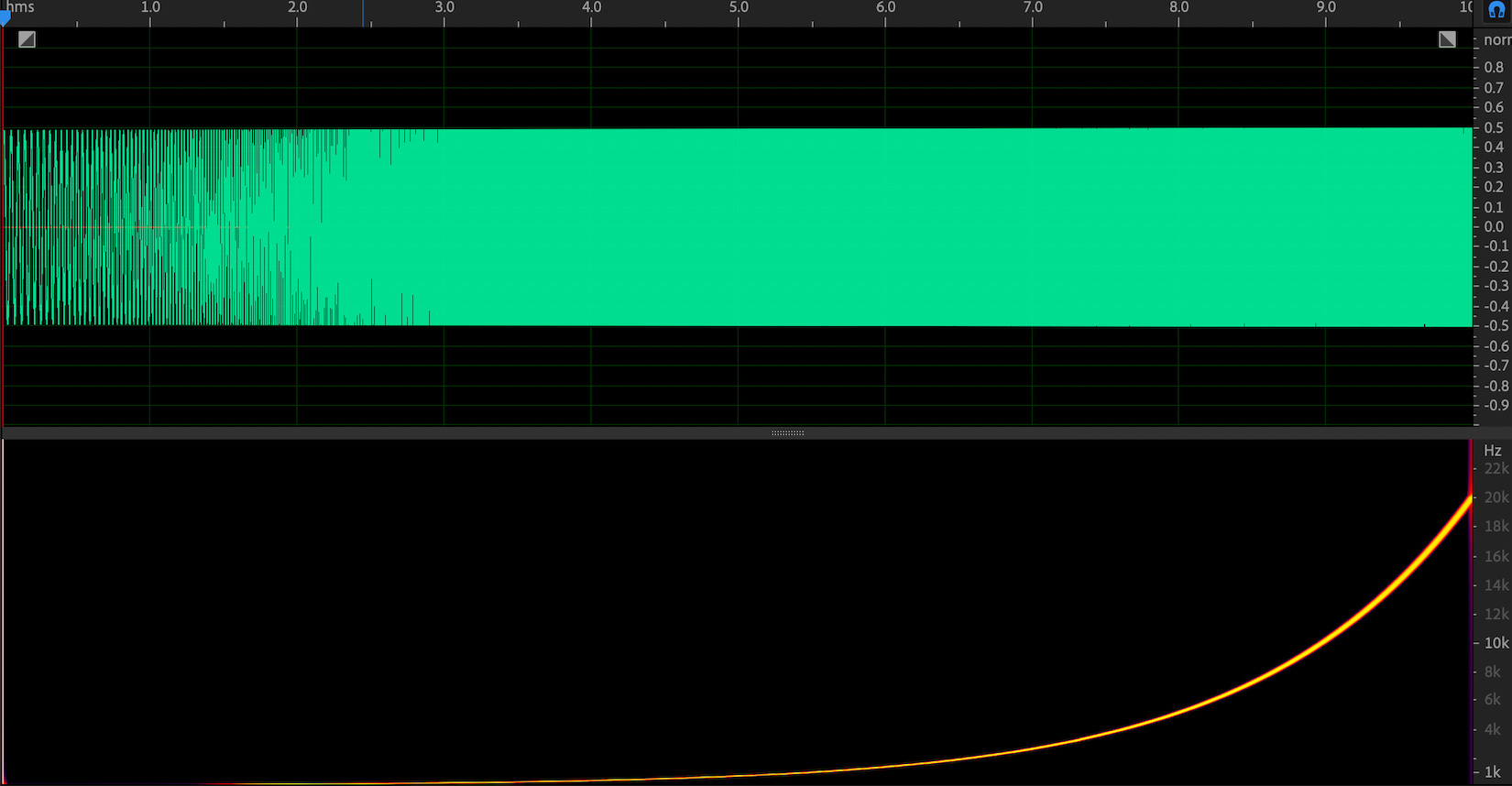
图 1. ESS 信号（频率轴为线性表示形式）

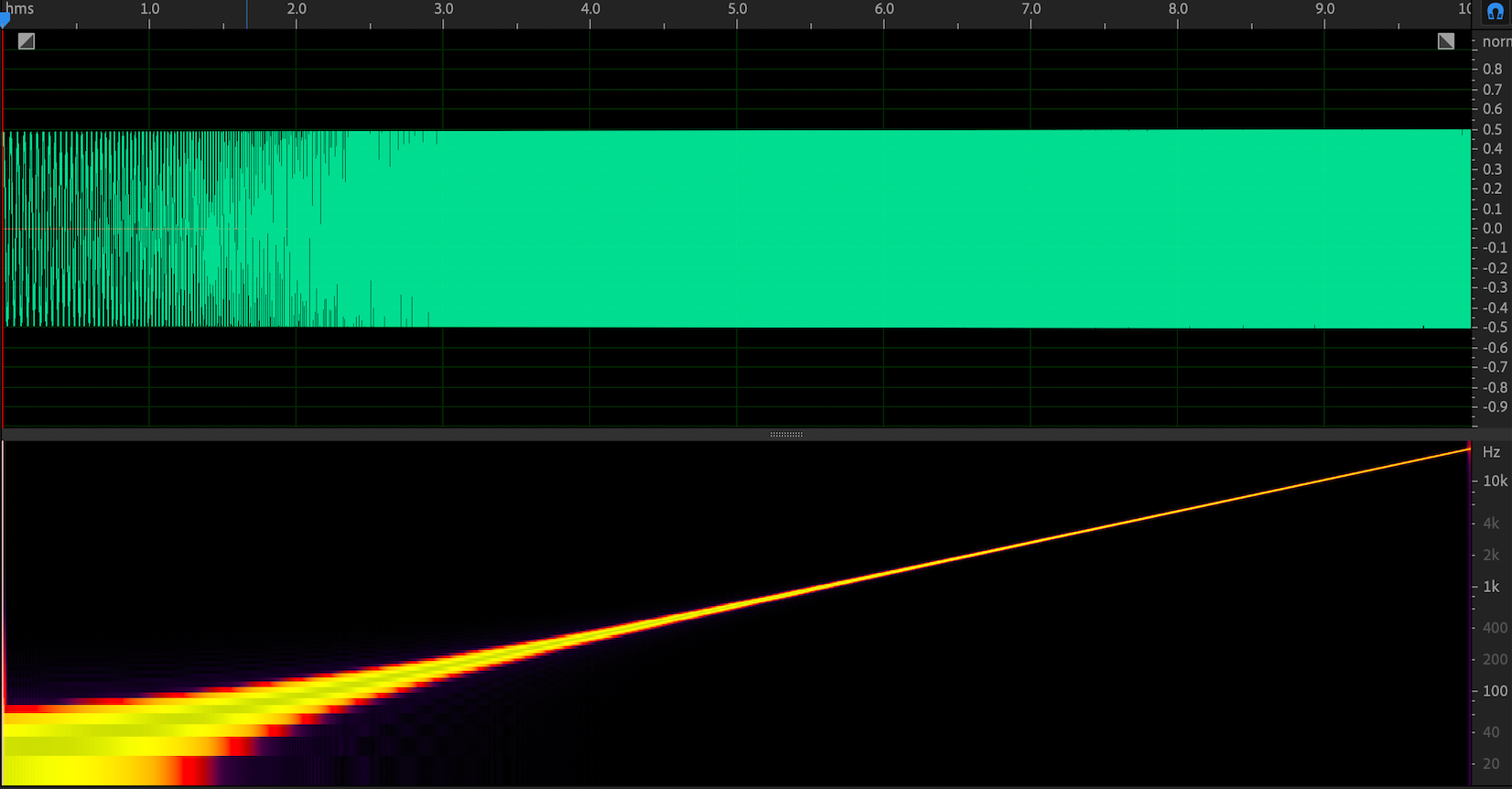
图 2. ESS 信号（频率轴为对数表示形式）

图 1 和图 2 展示了 ESS 信号在频率上的两种不同表现形式。图 1 中的频域轴是线性形式，其频谱图是指数函数的形式。图 2 中的频域轴是对数形式，其频谱图是线性函数的形式。

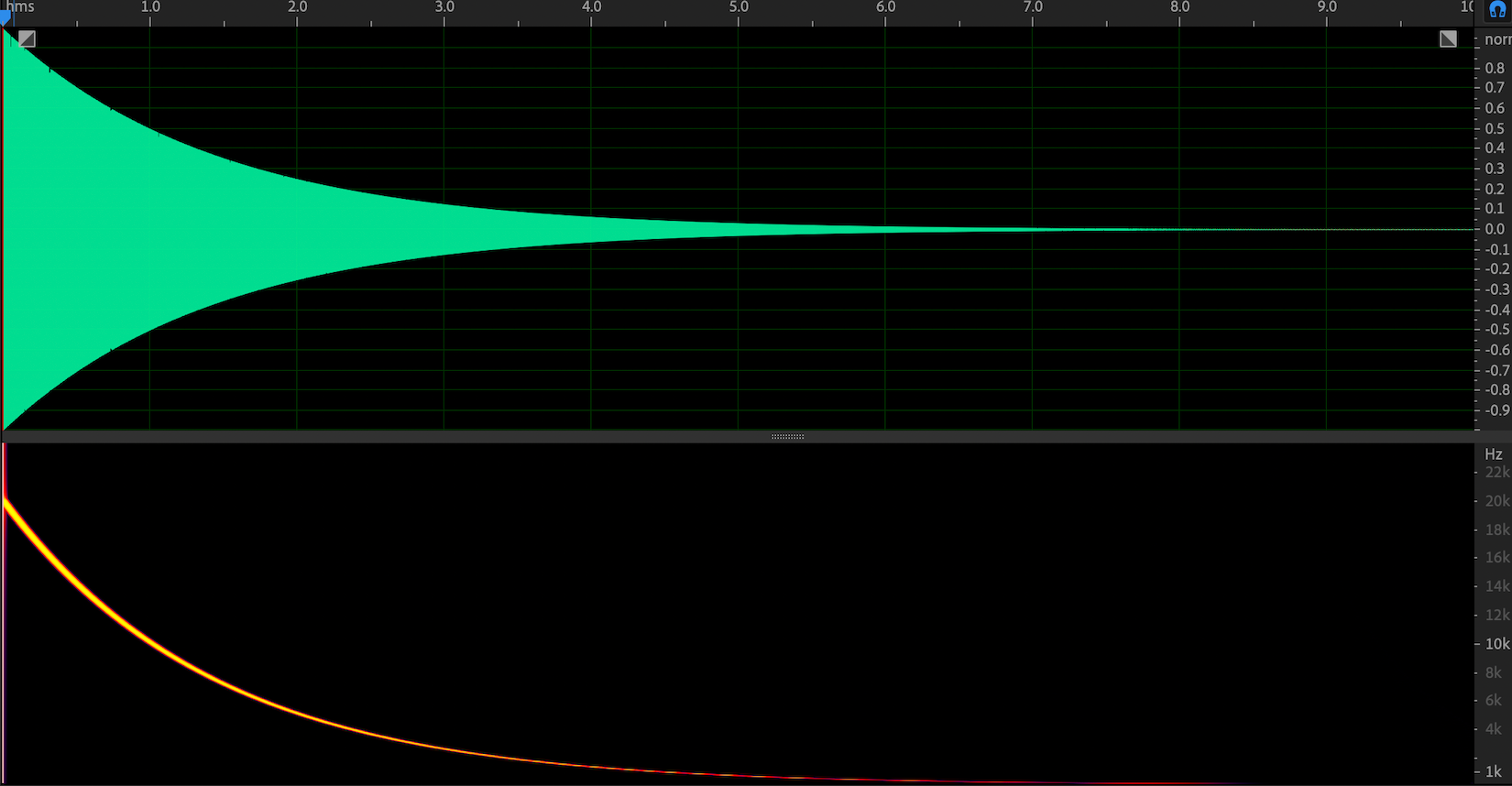
图 3. ESS 信号的卷积逆信号（频率轴为线性表示形式）

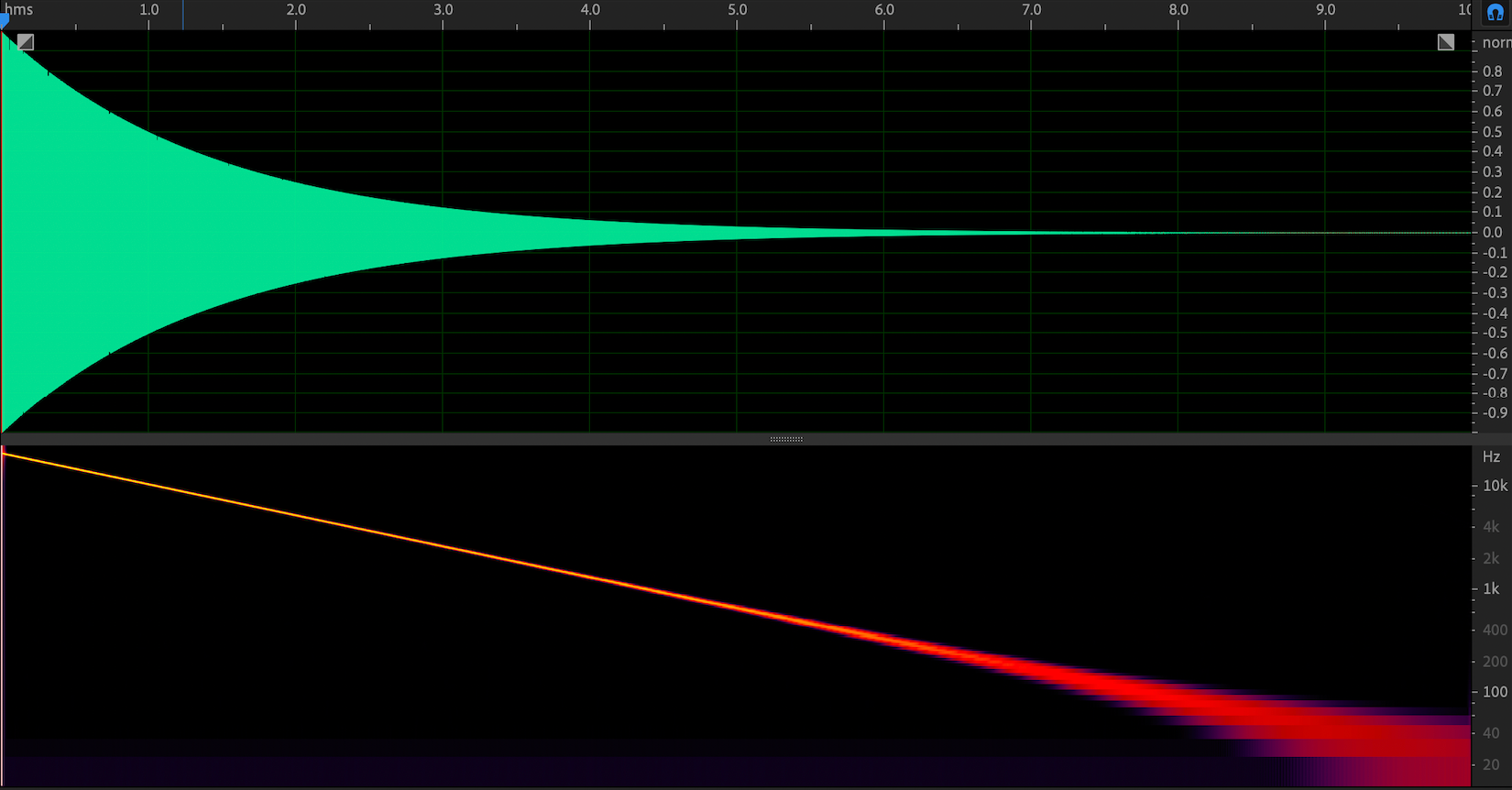
图 4. ESS 信号的卷积逆信号（频率轴为对数表示形式）

图 3 和图 4 展示了 ESS 信号的卷积逆信号在频率上的两种不同表现形式。图 3 中的频域轴是线性形式，图 4 中的频域轴是对数形式。

4. 测试步骤及代码

在知道了测试原理、ESS 信号和 ESS 信号的卷积逆信号后，该测试方法可以总结为：

使用扬声器播放 ESS 信号，即 x ( n ) x(n) x(n)；
麦克风采集得到信号 y ( n ) y(n) y(n)；
x − 1 ( n ) ∗ y ( n ) x^{-1}(n) * y(n) x−1(n)∗y(n) 的结果，就是测量得到的房间冲激响应；

以下为该测试方法所对应的 python 代码，在笔记本上运行该代码即可得到测量的房间冲激响应：

python 复制代码

import numpy as np
import soundfile as sf
import sounddevice as sd
import matplotlib.pyplot as plt
from scipy.signal import fftconvolve

# 1. 参数设置
fs = 48000        # 采样率 Hz
T = 10.0          # 扫频时长 s
f1 = 20.0         # 起始频率 Hz
f2 = 20000.0      # 结束频率 Hz

# =============================
# 1. 生成对数扫频信号
# =============================
t = np.linspace(0, T, int(fs*T), endpoint=False)
K = T / np.log(f2 / f1)
L = np.log(f2 / f1)

phase = 2 * np.pi * f1 * K * (np.exp(t / K) - 1)
sweep = np.sin(phase)

# =============================
# 2. 生成对数扫频信号的卷积逆信号
# =============================
env = np.exp(-t / K)
inverse_sweep = sweep[::-1] * env

# =============================
# 3. 播放并录音
# =============================
print("Recording...")
playback = np.concatenate((sweep, np.zeros(int(fs*2))))  # 加静音尾巴
record = sd.playrec(playback, samplerate=fs, channels=1, dtype='float64')
sd.wait()
print("Recording done.")

# =============================
# 4. 计算得到 RIR
# =============================
record = record[:,0]
rir = fftconvolve(record, inverse_sweep, mode='full')
impulse = fftconvolve(sweep, inverse_sweep, mode='full')

sf.write("ess.wav", sweep, fs, subtype="PCM_16")
sf.write("inverse_ess.wav", inverse_sweep, fs, subtype="PCM_16")
sf.write("rir.wav", rir/np.max(np.abs(rir)), fs, subtype="PCM_16")
sf.write("impulse.wav", impulse/np.max(np.abs(impulse)), fs, subtype="PCM_16")
sf.write("record.wav", record, fs, subtype="PCM_16")

一种房间冲激响应测量方法

目录

1. 引言

2. 原理

3. ESS 信号及其卷积逆信号

4. 测试步骤及代码