Simulink中卡尔曼滤波、高斯滤波与滑动平均滤波算法对比实战

simulink卡尔曼滤波算法demo，处理输入信号数据，与高斯滤波和滑动平均滤波算法做对比，可直接拿来修改使用

最近在做信号处理相关的项目，对Simulink里不同滤波算法有了不少实践经验，今天就来跟大家分享下卡尔曼滤波算法在Simulink中的实现，并且和高斯滤波、滑动平均滤波算法做个对比，给出的内容都是可直接拿来修改使用的。

一、卡尔曼滤波算法在Simulink中的实现

卡尔曼滤波是一种利用线性系统状态方程，通过系统输入输出观测数据，对系统状态进行最优估计的算法。在Simulink里实现卡尔曼滤波，我们可以借助相关的模块库。

首先，打开Simulink并新建一个模型。在Simulink库浏览器中，搜索"Kalman Filter"模块。这个模块通常在"Communications System Toolbox"或者"Signal Processing Toolbox"中（具体取决于你安装的MATLAB版本及相关工具箱）。

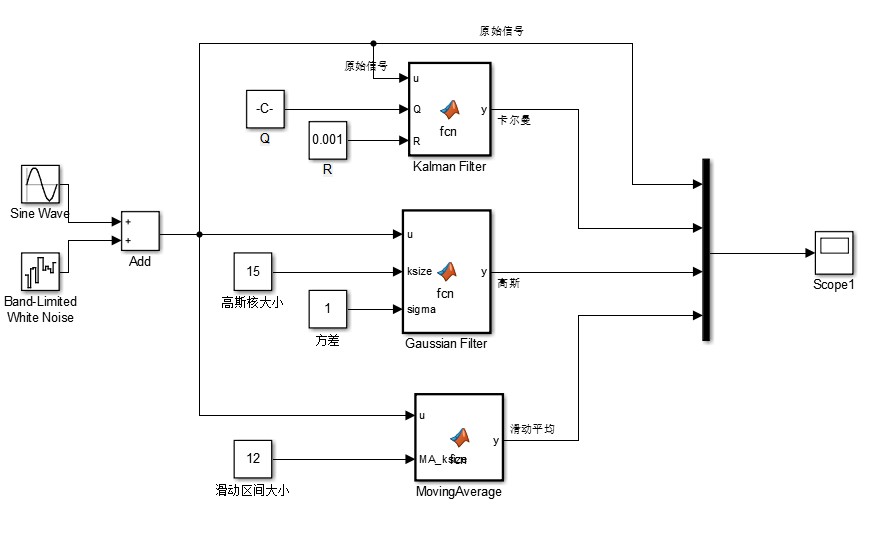
假设我们要处理一个简单的一维信号。创建输入信号源，例如使用"Step"模块或者"Signal Generator"模块来生成测试信号。将生成的信号连接到"Kalman Filter"模块的输入端口。

接下来配置"Kalman Filter"模块参数。这里需要设置状态转移矩阵、观测矩阵、过程噪声协方差、观测噪声协方差等关键参数。以一个简单的一维运动模型为例，状态转移矩阵 A = [1]，观测矩阵 H = [1]，过程噪声协方差 Q 和观测噪声协方差 R 根据实际信号噪声情况设定。

代码角度来看，虽然Simulink是图形化建模，但背后其实也是有对应代码逻辑的。如果要在MATLAB脚本中实现简单的卡尔曼滤波（这里用简单的一维情况示意）：

matlab 复制代码

% 初始化参数
A = 1; % 状态转移矩阵
H = 1; % 观测矩阵
Q = 0.01; % 过程噪声协方差
R = 0.1; % 观测噪声协方差
x_hat = 0; % 初始状态估计
P = 1; % 初始估计协方差

% 假设观测数据
z = [1.2, 1.3, 1.5, 1.4]; % 观测值序列

for k = 1:length(z)
    % 预测步骤
    x_hat_minus = A * x_hat;
    P_minus = A * P * A' + Q;
    
    % 更新步骤
    K = P_minus * H' / (H * P_minus * H' + R);
    x_hat = x_hat_minus + K * (z(k) - H * x_hat_minus);
    P = (eye(size(A)) - K * H) * P_minus;
end

上述代码简单实现了卡尔曼滤波的预测和更新步骤，在Simulink中的"Kalman Filter"模块其实就是对这个核心逻辑进行了封装，方便我们图形化使用。

二、高斯滤波算法

高斯滤波是一种线性平滑滤波，适用于消除高斯噪声，常用于图像处理，但也可用于一维信号处理。在Simulink中，可以自己搭建高斯滤波模块。

创建一个自定义的S - Function模块，在S - Function中编写高斯滤波算法。下面是一个简单的高斯滤波函数示例（以一维信号为例）：

matlab 复制代码

function y = gaussian_filter(x, sigma)
    n = length(x);
    half_width = floor(3 * sigma);
    w = zeros(1, 2 * half_width + 1);
    for i = -half_width:half_width
        w(i + half_width + 1) = exp(-i^2 / (2 * sigma^2)) / (sqrt(2 * pi) * sigma);
    end
    y = conv(x, w, 'same');
end

在这个函数中，我们首先计算高斯核 w，然后使用 conv 函数对输入信号 x 进行卷积操作，得到滤波后的信号 y。在Simulink的S - Function模块中，将这个函数逻辑集成进去，就可以实现高斯滤波对输入信号的处理。

三、滑动平均滤波算法

滑动平均滤波是一种简单的滤波算法，它对连续的N个采样值进行平均，以得到滤波后的输出。在Simulink里实现也很容易，使用"Moving Average"模块即可。

该模块有一个参数"Length"，用于设置参与平均的采样点数N。假设我们设置"Length = 5"，那么就是对最近的5个采样值进行平均。

从代码角度看，滑动平均滤波的实现也非常直观：

matlab 复制代码

function y = moving_average_filter(x, N)
    n = length(x);
    y = zeros(size(x));
    for k = 1:n
        if k < N
            y(k) = sum(x(1:k)) / k;
        else
            y(k) = sum(x(k - N + 1:k)) / N;
        end
    end
end

上述代码遍历输入信号 x，根据当前位置 k 和设置的平均点数 N 来计算滑动平均后的输出 y。

四、三种滤波算法对比

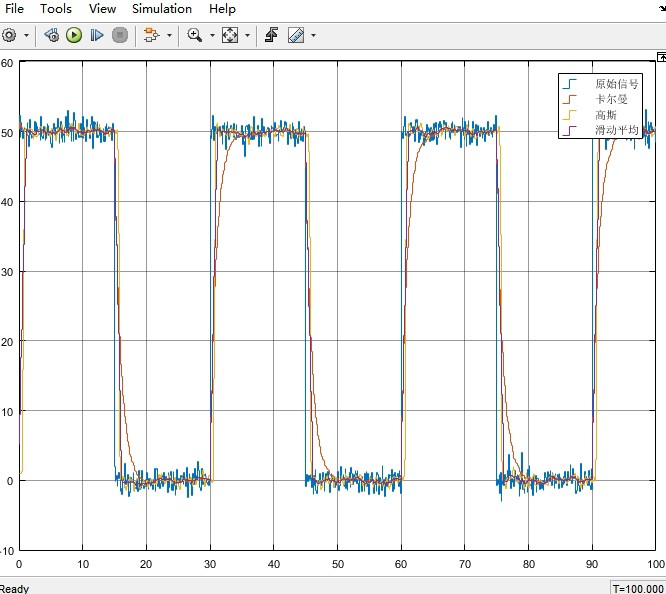
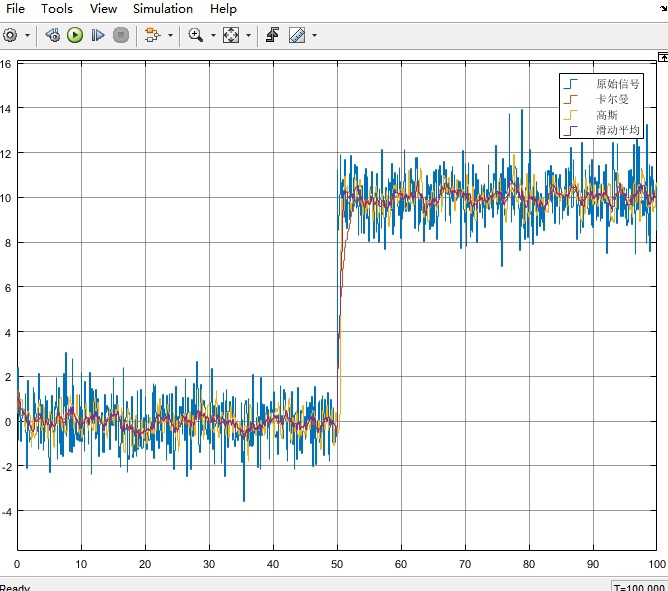
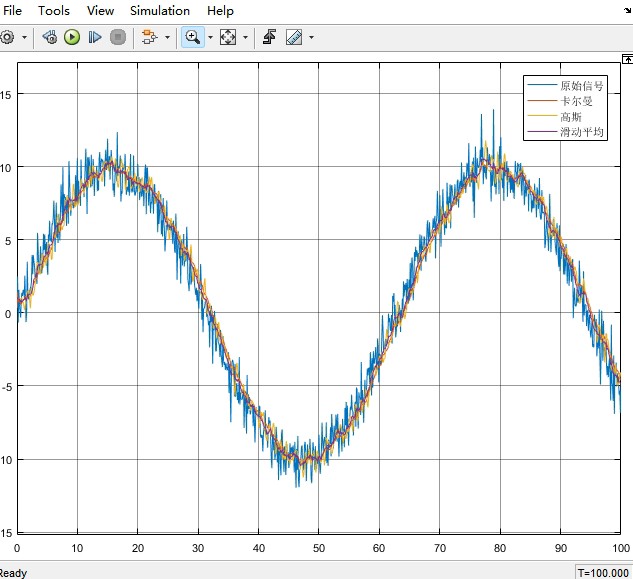
将这三种滤波算法同时应用到同一输入信号上，观察其滤波效果。以一个带有噪声的正弦信号作为输入信号为例。

通过对比可以发现，卡尔曼滤波对于动态变化的信号有较好的跟踪能力，能够在抑制噪声的同时较好地保留信号的动态特性；高斯滤波在去除高斯噪声方面表现出色，使信号更加平滑，但可能会使信号的细节有所损失；滑动平均滤波实现简单，对于稳定的噪声有一定的滤波效果，但在信号快速变化时，可能会出现较大的延迟。

希望通过这次分享，大家对Simulink中的这三种滤波算法有更清晰的认识，能够根据实际需求选择合适的滤波算法。大家在实践过程中有任何问题，欢迎留言交流。