在行列可自由变换的平面上2点结构有3个
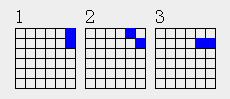
现在设所有点必须至少与其余一个点相连,且有一个点位于坐标原点。
|---|---|---|---|---|----|--------------------------|
| 1 | | | | | | |
| 1 | | | | | z1 | 1*(cos90+i sin90) |
| | | | | | | |
| 1 | | | | | z2 | 1*(cos(-90)+i sin(-90)) |
| 1 | | | | | | |
则2a1只有两种可能,分别对应两个复数z1,z2,这两个复数出现的概率相同,所以2a1用复数表示就是1*(cos0+i sin0)||1*(cos(-90)+i sin(-90)),z1||z2。
|---|---|---|---|---|---|----|---------------------------|
| | | 1 | | | | | |
| | 1 | | | | | z1 | 2^0.5*(cos45+i sin45) |
| | | | | | | | |
| 1 | | | | | | | |
| | 1 | | | | | z2 | 2^0.5*(cos135+i sin135) |
| | | | | | | | |
| | 1 | | | | | z3 | 2^0.5*(cos225+i sin225) |
| 1 | | | | | | | |
| | | | | | | | |
| | 1 | | | | | z4 | 2^0.5*(cos315+i sin315) |
| | | 1 | | | | | |
同样的方法,2a2对应的是4个复数,z1,z2,z3,z4,所以2a2用复数表示就是z1||z2||z3||z4。
这4个状态模长相同,幅角只能是4个整数。
|---|---|---|---|---|---|----|----------------------|
| | 1 | 1 | | | | z1 | 1*(cos0+i sin0) |
| | | | | | | | |
| 1 | 1 | | | | | z2 | 1*(cos180+i sin180) |
所以用复数表示2a3就是z1||z2
所以如果有一个点就是在两个状态1*(cos0+i sin0),1*(cos180+i sin180) 间循环往复的运动,这一运动状态就是2a3.
所有的多点结构都可以用两点结构表示,所以任一个多点结构都对应一个复数的集合,模长和幅角有多个离散值。
|---|---|---|---|---|---|---|---|---|--------|---|-------|
| | | | | | | | | | r | | θ |
| 1 | | | | | | 1 | | | 1 | | 0 |
| | | | | 1 | 1 | | | | 5^0.5 | | 26.57 |
如结构3a4的一个状态一个点的模长是1幅角是0,一个点的模长是5^0.5,幅角是26.57,所以这个状态对应2个复数,这两个复数的夹角是26.57度
像这样模长是1和5^0.5,,夹角是26.57的状态共有4个
|---|---|---|---|---|---|---|---|---|--------|---|-------|---|--------|
| | | | | | | | | | r | | θ | | Δθ |
| 1 | | | | | | 1 | | | 1 | | 0 | | 26.565 |
| | | | | 1 | 1 | | | | 5^0.5 | | 26.57 | | |
| | | | | | | | | | | | | | |
| 2 | | | | 1 | 1 | | | | 5^0.5 | | 333.4 | | 26.6 |
| | | | | | | 1 | | | 1 | | 360 | | |
| | | | | | | | | | | | | | |
| 3 | | 1 | | | | | | | 5^0.5 | | 153.4 | | 26.565 |
| | | | 1 | 1 | | | | | 1 | | 180 | | |
| | | | | | | | | | | | | | |
| 4 | | | 1 | 1 | | | | | 1 | | 180 | | 26.565 |
| | | 1 | | | | | | | 5^0.5 | | 206.6 | | |
还有4个状态模长是5^0.5,2^0.5夹角是18.4度
|---|---|---|---|---|---|---|---|---|--------|---|-------|---|--------|
| | | | | | | | | | r | | θ | | Δθ |
| 5 | | | | | 1 | 1 | | | 5^0.5 | | 26.57 | | 18.435 |
| | | | | 1 | | | | | 2^0.5 | | 45 | | |
| | | | | | | | | | | | | | |
| 6 | | | | 1 | | | | | 2^0.5 | | 315 | | 18.4 |
| | | | | | 1 | 1 | | | 5^0.5 | | 333.4 | | |
| | | | | | | | | | | | | | |
| 7 | | 1 | 1 | | | | | | 2^0.5 | | 135 | | 18.435 |
| | | | | 1 | | | | | 5^0.5 | | 153.4 | | |
| | | | | | | | | | | | | | |
| | | | | | | | | | | | | | |
| 8 | | | | 1 | | | | | 5^0.5 | | 206.6 | | 18.435 |
| | | 1 | 1 | | | | | | 2^0.5 | | 225 | | |
还有4个状态模长是2,2^0.5,夹角是45度
|----|---|---|---|---|---|---|---|---|---|---|-----|---|----|
| | | | | | | | | | r | | θ | | Δθ |
| 9 | | | | | 1 | | | | 2 | | 0 | | 45 |
| | | | | 1 | | 1 | | | 2^0.5 || 45 | | |
| | | | | | | | | | | | | | |
| 10 | | | | 1 | | 1 | | | 2^0.5 || 315 | | 45 |
| | | | | | 1 | | | | 2 | | 360 | | |
| | | | | | | | | | | | | | |
| 11 | | 1 | | 1 | | | | | 2 | | 180 | | 45 |
| | | | 1 | | | | | | 2^0.5 || 225 | | |
| | | | | | | | | | | | | | |
| 12 | | | 1 | | | | | | 2^0.5 || 135 | | 45 |
| | | 1 | | 1 | | | | | 2 | | 180 | | |
还有两个模长是2^0.5,夹角是90度
|----|---|---|---|---|---|---|---|---|--------|---|-----|---|----|
| | | | | | | | | | r | | θ | | Δθ |
| 13 | | | 1 | | 1 | | | | 2^0.5 | | 45 | | 90 |
| | | | | 1 | | | | | 2^0.5 | | 135 | | |
| | | | | | | | | | | | | | |
| 14 | | | | 1 | | | | | 2^0.5 | | 225 | | 90 |
| | | | 1 | | 1 | | | | 2^0.5 | | 315 | | |
| | | | | | | | | | | | | | |
所以结构3a4一定能用28个复数表示。结构3a4在行列可自由变换的平面上彼此相连的运动,就是这14组28个复数之间的变换。
|---|---|---|---|---|----|--------------------------|
| 1 | | | | | | |
| 1 | | | | | z1 | 1*(cos90+i sin90) |
| | | | | | | |
| 1 | | | | | z2 | 1*(cos(-90)+i sin(-90)) |
| 1 | | | | | | |
2a1对应的两个复数就是z1=i,z2=-i,z1*z2=1.
所以在考虑方向的前提下结构是可逆的
|---|----|---|---|---|
| 1 | | 1 | | |
| 1 | * | 1 | = | 1 |
所以一个结构可以理解为一个函数,只不过这个函数的自变量是有限个复数,3a14可能有14种不同的变化,如果在力的作用下变成了一种或几种的组合,比如13和14共存在状态,这个状态的外在表现应该就是一种位置概率。