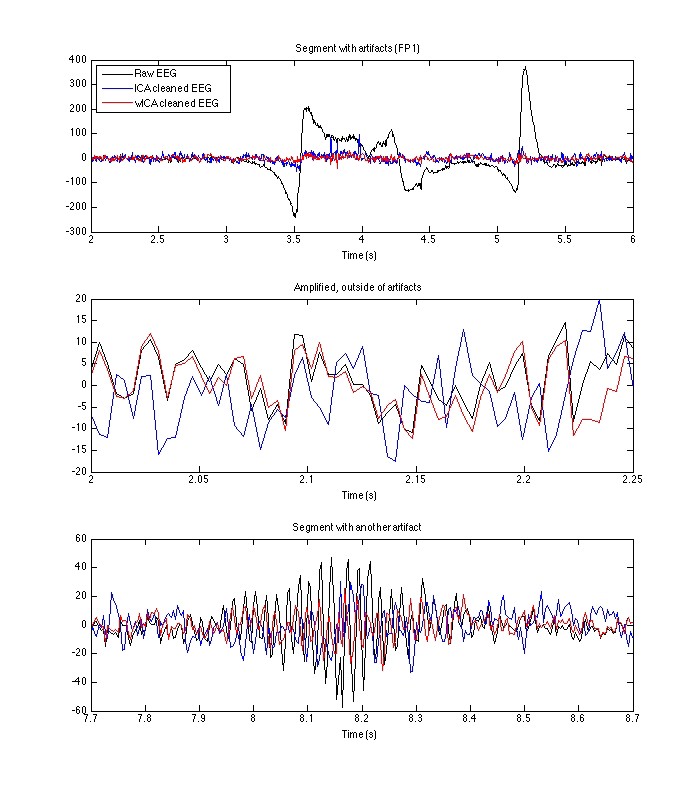
一种增强的独立分量分析方法-基于小波域（MATLAB R2018B） 压缩包=数据＋代码+参考...

一种增强的独立分量分析方法-基于小波域（MATLAB R2018B） 压缩包=数据＋代码+参考。 wavParam.nAngs = 32; wavParam.nScls = 12; wavParam.minWaveLength = 6; wavParam.mult = 1.2; wavParam.radSigma = 0.55; wavParam.angSigma = 0.2;

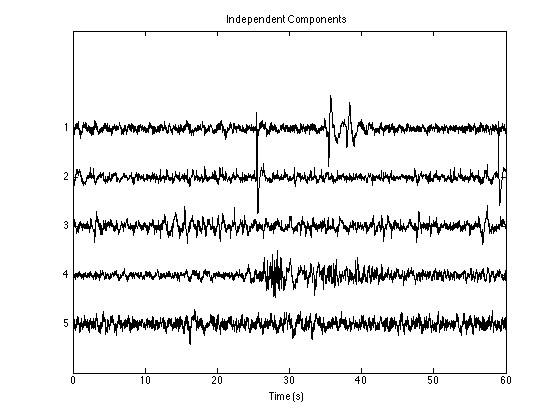
小波域独立分量分析（ICA）总带着点玄学色彩，但今天咱们换个角度，直接掀开代码看门道。先看这段参数配置，像不像游戏里的技能树？nAngs=32意味着把小波滤波器的方向拆成32个角度，nScls=12则是搞了12层不同尺度的滤波器组。好比拿着显微镜从不同角度和放大倍数观察信号。

% 小波参数配置的黄金分割点
wavParam.minWaveLength = 6;  % 最小波长不能太短，否则噪声比亲妈还亲
wavParam.mult = 1.2;         % 每次放大1.2倍，等比数列的魔法
wavParam.radSigma = 0.55;    % 径向高斯滤波器的胖瘦控制
wavParam.angSigma = 0.2;     % 角度方向的高斯瘦身秘诀

重点看看滤波器生成的核心代码段。这个logGabor函数可不是随便调个库，而是手动实现径向和角度分量相乘。注意exp指数里的计算，radSigma控制径向带宽，angSigma管角度扩散范围。当信号经过这组滤波器后，时频特征就像被X光切片了一样。

function [filter] = logGabor(wavParam, angle, scale)
    % 生成对数高斯核
    radius = wavParam.minWaveLength * wavParam.mult^(scale-1);
    radFilt = exp(-(log(radius/wavParam.minWaveLength)).^2/(2*log(wavParam.radSigma)^2));
    
    % 角度分量计算
    angFilt = exp(-(angle - pi/2).^2/(2*wavParam.angSigma^2));
    
    filter = radFilt .* angFilt; % 合体成为二维滤波器
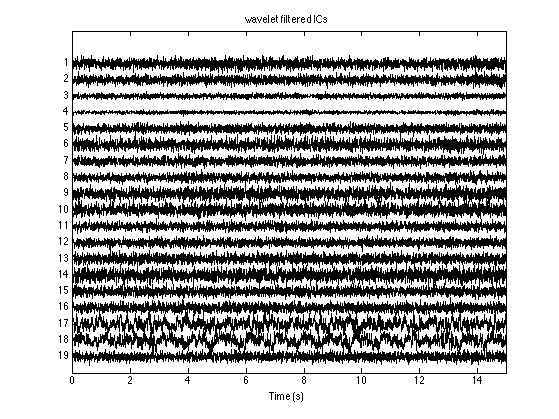
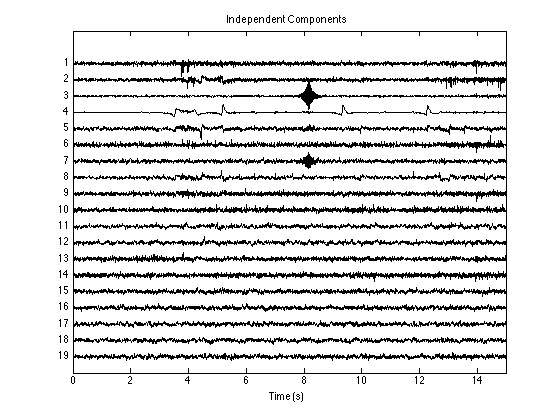
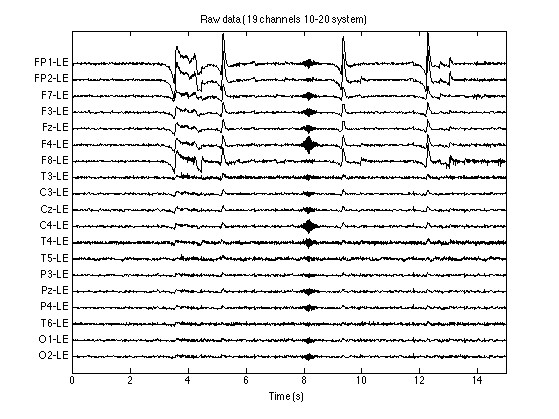
end

实战中经常遇到信号突变点定位不准的问题。这时候小波域的优势就出来了------在某个特定尺度的滤波器输出中，突发噪声会呈现明显的尖峰特征。比如下面这段时频能量统计代码，通过寻找能量突变的尺度层，能自动标记可疑干扰区间：

energy = squeeze(sum(abs(waveletCoeff).^2, [1,2])); % 挤压多余维度
abnormalFrames = find(energy > mean(energy)*2.5);   % 简单粗暴的阈值法

不过要注意mult参数的设置，1.2这个值经过多次实测，能在频率分辨率和计算开销之间取得平衡。如果设置成1.1，虽然频率更细腻，但内存消耗可能直接起飞。有次手滑设成1.5，结果高频段直接漏检重要成分，翻车现场堪比秋名山漂移。

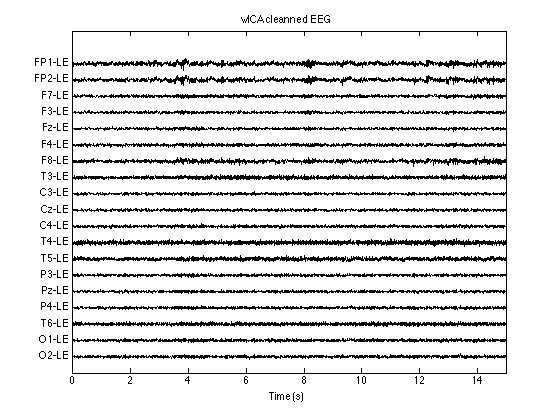
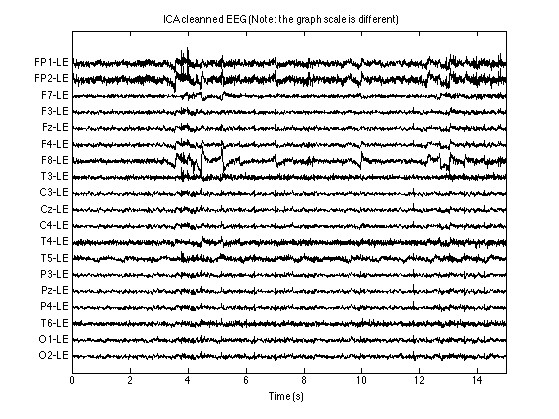
分离效果评估也不能只看信噪比数值。建议可视化混合信号的时频图和分离后的分量对比，特别是注意在信号交汇处是否有鬼影残留。有时候调大angSigma到0.3，虽然理论上的角度分辨率下降，但实际效果反而更干净，这大概就是玄学实践超越理论的时刻吧。