AI+材料表征（二）

系列文章目录

文章目录

系列文章目录
📌1.材料专家------用于材料发现的人工智能
[📌 2 适用于元素周期表的通用图深度学习原子间势](#📌 2 适用于元素周期表的通用图深度学习原子间势)
📌3.利用少样本机器学习实现电子显微镜数据的快速灵活分割

📌1.材料专家------用于材料发现的人工智能

Materials Expert-Artificial Intelligence for materials discovery communications materials

主要贡献

提出了一种新的机器学习框架 ME-AI，该框架通过结合人类专家的直觉和实验数据，发掘新的描述符来预测材料的性质。以下是这篇文章的主要贡献和创新点：

核心贡献：

ME-AI框架：这个机器学习模型将专家策划的数据与实验数据结合，通过从中提取定量描述符来预测材料性质，特别是针对拓扑半金属（TSMs）在方形网状材料中的识别。
专家知识与机器学习的结合：文章的创新之处在于，将材料专家的直觉和经验通过实验数据"封装"成机器学习模型的输入，从而揭示出能有效预测材料性质的新的量化描述符。

主要创新点：

自动发现新的描述符：在方形网状材料的数据库上，ME-AI不仅重新发现了传统的 t因子（t-factor），还发现了四个新的描述符。其中一个新的描述符与化学中的超价化学（hypervalency）概念相关，能够帮助识别拓扑半金属。
拓扑绝缘体预测：通过将ME-AI框架应用于由专家标记的879个方形网状材料，模型能够有效地识别拓扑半金属，并且能够将这种识别能力扩展到其他材料结构，如岩盐结构，展示了模型的普适性和迁移能力。
新的化学理解：通过机器学习提取的描述符，文章揭示了超价化学对于拓扑半金属形成的关键作用，特别是 χ_sq*fcc 描述符，它反映了在方形网状材料中原子间的共价键合，能够帮助理解这些材料的电子结构。
高准确率和泛化能力：该模型通过高斯过程回归（Gaussian Process Regression，GPR）进行了训练，展示了极高的准确性（超过98%），并且能够从方形网状材料推广到其他结构类型（如岩盐结构），进一步证明了其通用性和稳定性。

摘要

材料数据库的发展为挖掘可预测新兴性质的描述符创造了机遇，但多数研究依赖高通量从头算计算，这类计算结果可能与实验存在偏差。实验研究者则依赖实践积累的直觉。我们提出"材料专家-人工智能"（ME-AI）------这是一个机器学习框架，可将此类直觉转化为从机器测量数据中提取的定量可解释描述符。

我们以12个实验特征描述的879种方网化合物为数据集，训练了带有化学感知核的狄利克雷基高斯过程模型。ME-AI不仅复现了识别拓扑半金属（TSM）的已知专家规则，还揭示了"超价性"是这类体系的关键化学调控因素；更值得注意的是，仅用方网TSM数据训练的模型，能正确分类岩盐结构中的拓扑绝缘体，体现出良好的迁移性。

该框架可与电子结构理论互补，能随数据库扩容而扩展，嵌入了专家知识、提供了可解释判据，还能指导靶向合成，从而加速不同化学家族的材料发现与快速实验验证。

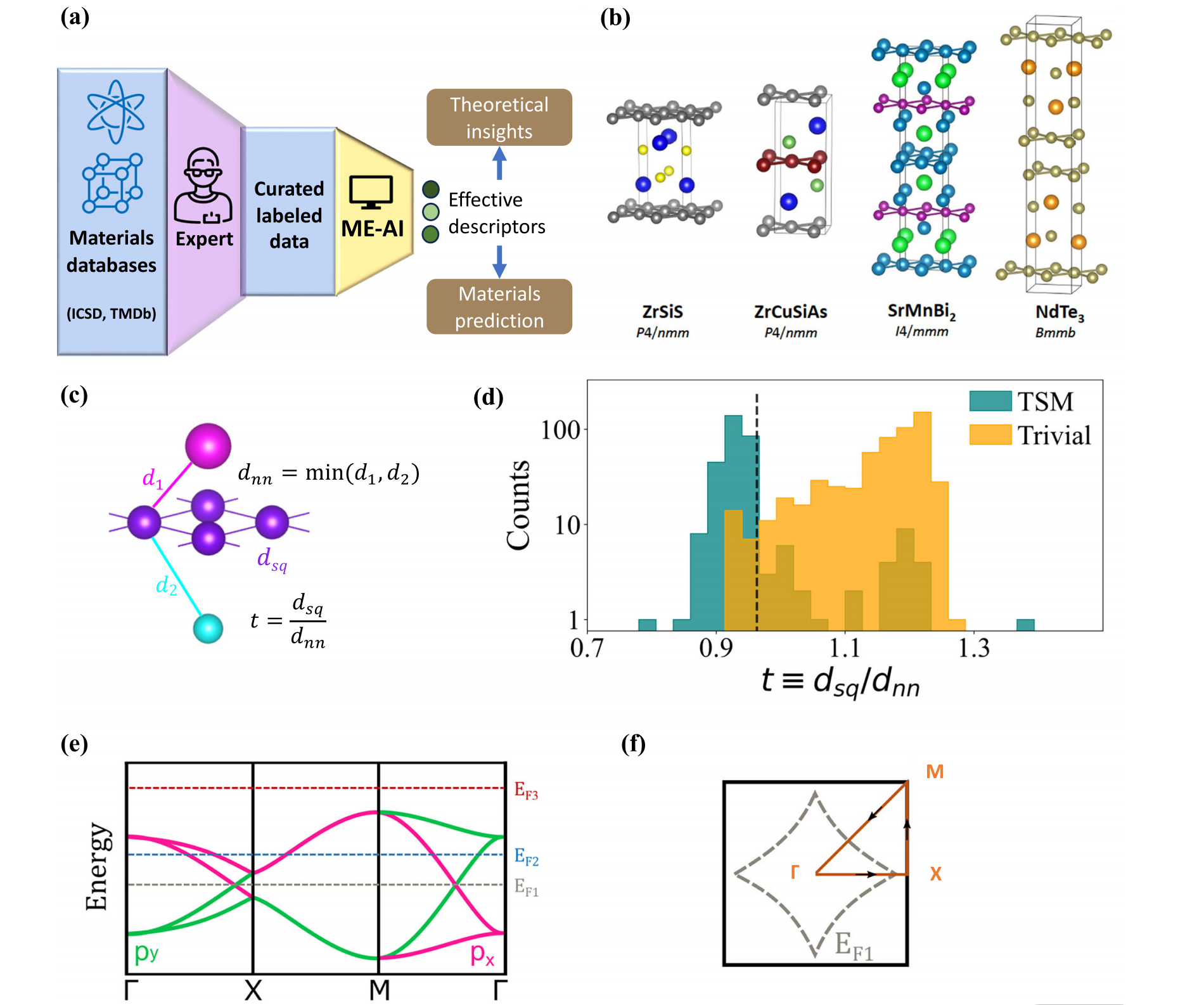
图1 | 用于方网材料中拓扑半金属研究的"材料专家-人工智能"（ME-AI）
a a a ME-AI的概念框架。
b b b 部分二维方网材料的晶体结构。
c c c 三维方网结构：面外的品红色与青色原子到方网平面（紫色）的距离分别为 d 1 d_1 d1和 d 2 d_2 d2；容忍因子定义为 t ≡ d sq / d nn t \equiv d_{\text{sq}}/d_{\text{nn}} t≡dsq/dnn，其中 d nn ≡ min ⁡ ( d 1 , d 2 ) d_{\text{nn}} \equiv \min(d_1, d_2) dnn≡min(d1,d2)代表面外最近邻间距。

d 数据集中标记为拓扑半金属（青绿色）与平庸材料（橙色）的化合物的容忍因子 t t t分布（其中 t ≡ d sq / d nn t \equiv d_{\text{sq}}/d_{\text{nn}} t≡dsq/dnn， d nn d_{\text{nn}} dnn为面外最近邻间距）；我们发现 t ≈ 0.96 t \approx 0.96 t≈0.96（虚线）能以最高准确率区分拓扑半金属与平庸材料。
e e e 方网形成过程中假设的 p x p_x px（粉色）与 p y p_y py（绿色）轨道的紧束缚能带结构，沿f图所示路径绘制；图中展示了两处伴随能带反转的对称保护交叉点；费米能级的位置决定了材料是能带绝缘体（ E F 3 E_{\text{F}3} EF3）、金属（ E F 2 E_{\text{F}2} EF2）还是拓扑半金属（ E F 1 E_{\text{F}1} EF1）。
f f f 布里渊区（ B Z BZ BZ）：当费米能级调至穿过节线时，节线即为费米面。

正文

过去十年的全球努力构建了庞大的材料数据库¹⁻¹¹，让研究者可查询单个条目的关联数据。这个"材料数据时代"为通过推导条目间的关联与趋势来发现物理性质描述符，提供了前所未有的机遇。历史上最成功的案例是门捷列夫：他通过元素周期表的经验趋势预测了元素材料的性质。但发现非元素材料的拓扑特征仍极具挑战------这类材料的组合相空间与特征空间的高维度，已超出人工探索的范围。

机器学习（ML）工具的普及推动了近期进展²³⁻²⁴：研究者通过扩大从头算计算与合成规模筛选稳定材料。但从头算预测的局限在于，无法囊括实验研究者多年积累的直觉与经验。我们的目标是将专家（ME）的直觉（辅以材料性质标注）转化为ML模型，让ME-AI从实验数据中提取信息、明确这些直觉（见图1a）。

拓扑半金属（TSM）因新奇物理性质与应用潜力受关注²⁵⁻²⁷，其核心特征是"自旋简并能带交叉的节线"与"费米能级调控至节线处"。传统TSM识别需分析材料对称性、推导能带表示，但我们观察到：化学直觉可助力在二维"方网材料"中预测TSM（这类材料是含2D中心方网的固体，见图1b、c）。基于这一直觉，我们在文献26、27中引入"容忍因子（t因子）"------定义为"方网晶格间距与面外最近邻间距的比值"（图1c），它能有效区分TSM（t值较小）与平庸材料（图1d）。

为保证完整性，我们先回顾t因子的结构逻辑：方网材料的二维方网基序层间堆叠着其他原子；若通过二维紧束缚模型（将面外原子投影至方网中心、方网原子pₓ/pᵧ轨道部分填充）最小化面外原子的影响，其能带结构会预测出"受对称性保护的拓扑节线"（图1e、f）。若该模型成立且费米能级穿过节线，这类材料就是TSM²⁹。这启发我们用t因子（dₛq/dₙₙ）量化与二维方网平面的偏离程度，但3D晶体的低能电子性质还取决于电子填充、干扰能带与费米能级位置³⁰。

本研究核心

我们开发的ME-AI框架，利用实验整理的专家直觉挖掘TSM的定量描述符：将其应用于879种方网化合物（12个核心特征）后，ME-AI不仅识别出"容忍因子"，还发现了4个新描述符（其中一个纯原子描述符契合"超价性、津特耳线"等经典化学概念）。它不仅预测能力优异，还能迁移至岩盐结构中识别拓扑绝缘体------这凸显了"人类专家知识+人工智能"在靶向材料发现中的潜力。

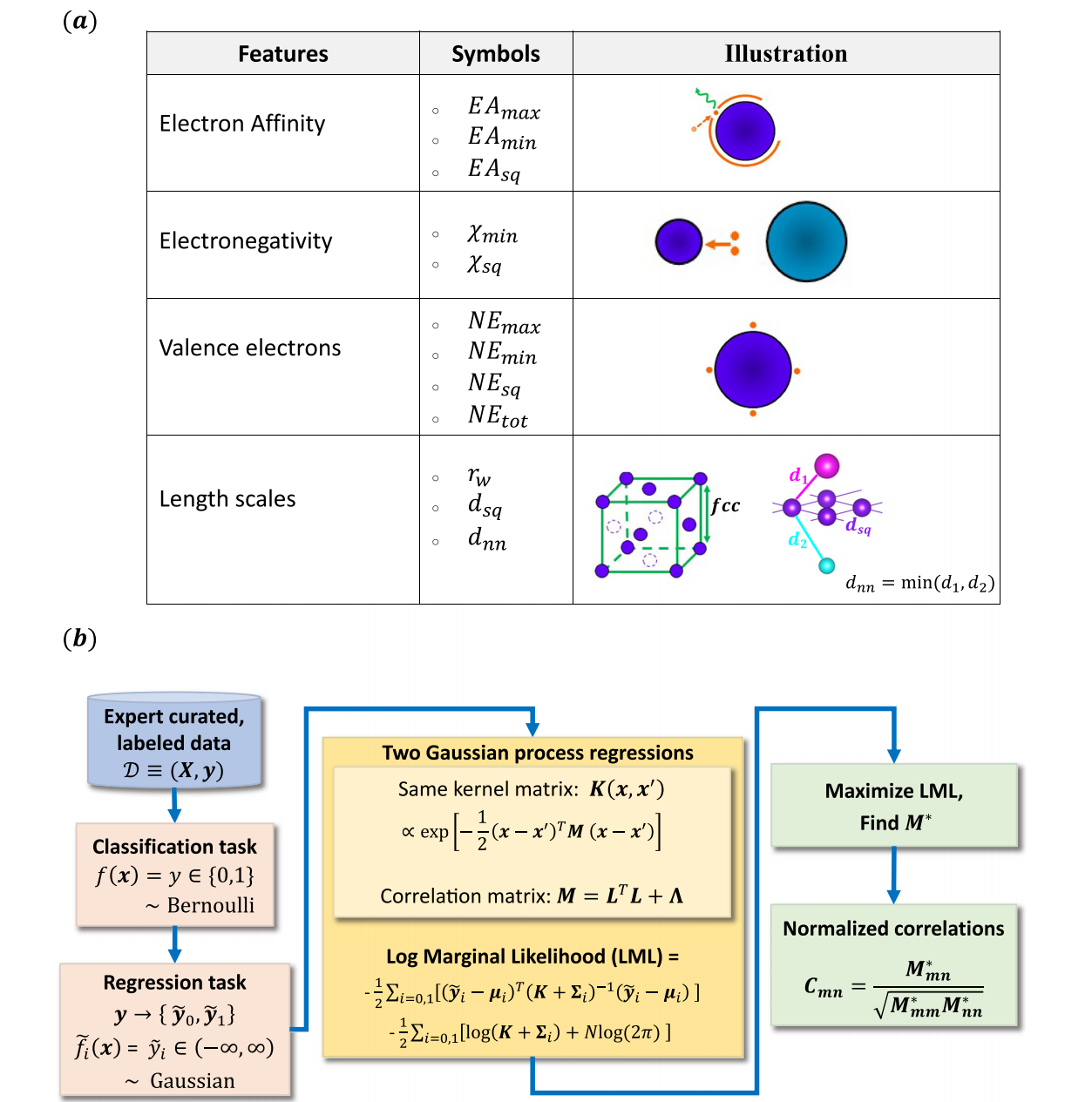
图2 | ME-AI的机器学习方案

a 核心特征。下标 max \text{max} max、 min \text{min} min、 sq \text{sq} sq分别代表最大值、最小值、方网元素对应的值；下标 tot \text{tot} tot代表基于化学计量信息的总电子数。我们省略了 χ max \chi_{\text{max}} χmax，因其与 χ sq \chi_{\text{sq}} χsq的协方差较高。

b ME-AI的流程图解。我们首先构建预处理并标注的数据集 D ≡ ( X , y ) \mathcal{D} \equiv (X, y) D≡(X,y)：其中包含12个核心特征（ X = ( x 1 , . . . , x N ) X = (x_1, ..., x_N) X=(x1,...,xN)， x n ∈ R D x_n \in \mathbb{R}^D xn∈RD， D = 12 D=12 D=12），以及对应的类别标签（ y = ( y 1 , . . . , y N ) y = (y_1, ..., y_N) y=(y1,...,yN)， y n ∈ { 0 , 1 } y_n \in \{0,1\} yn∈{0,1}）；下标(n)代表数据集中的不同材料（共 N N N个条目）。将分类任务转化为两个独立的回归任务后，我们基于共享核函数 K ( x , x ′ ) K(x, x') K(x,x′)搭建了两个高斯过程回归（GPR）模型。

核函数内部的相关矩阵(\mathbf{M})会耦合不同的核心特征，其设计采用因子分析结构 M = L L T + Λ \mathbf{M} = \mathbf{L}\mathbf{L}^T + \mathbf{\Lambda} M=LLT+Λ------这能让我们以有限的超参数学习不同核心特征（PF）间的相互作用。我们通过最大化对数边缘似然训练整个数据集的模型，这一过程会自动实现正则化。核心特征间的相关性 M ∗ M^* M∗可从训练后的模型参数中得到：第 m m m个与第 n n n个核心特征的耦合程度由标准化相关系数 C m n C_{mn} Cmn衡量，这能揭示识别方网拓扑半金属（TSM）的关键特征对。

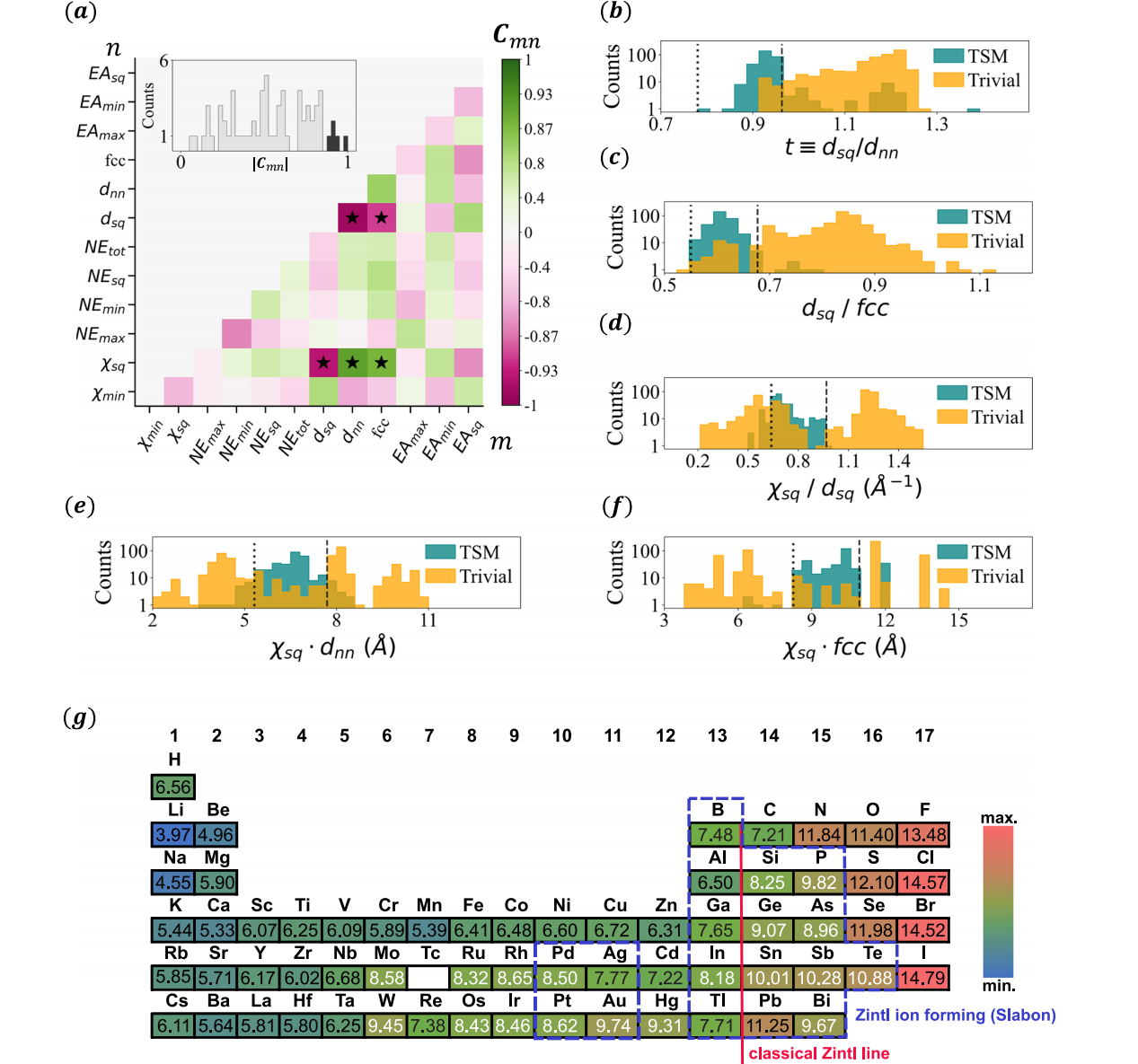
图3 | ME-AI的主要结果

图中展示了标准化相关矩阵 C m n C_{mn} Cmn（ m m m、 n n n代表核心特征），仅呈现下三角部分；插图为非对角元素 ∣ C m n ∣ |C_{mn}| ∣Cmn∣的大小分布，黑色标注的是最强元素。关键特征对 ( d sq , d nn ) (d_{\text{sq}}, d_{\text{nn}}) (dsq,dnn)、 ( d sq , fcc ) (d_{\text{sq}}, \text{fcc}) (dsq,fcc)、 ( χ sq , d sq ) (\chi_{\text{sq}}, d_{\text{sq}}) (χsq,dsq)、 ( χ sq , d nn ) (\chi_{\text{sq}}, d_{\text{nn}}) (χsq,dnn)、 ( χ sq , fcc ) (\chi_{\text{sq}}, \text{fcc}) (χsq,fcc)用星号标记。

b d sq / d nn d_{\text{sq}}/d_{\text{nn}} dsq/dnn、c d sq / fcc d_{\text{sq}}/\text{fcc} dsq/fcc、d χ sq / d nn \chi_{\text{sq}}/d_{\text{nn}} χsq/dnn、e χ sq ⋅ d nn \chi_{\text{sq}} \cdot d_{\text{nn}} χsq⋅dnn、f χ sq ⋅ fcc \chi_{\text{sq}} \cdot \text{fcc} χsq⋅fcc在数据集中拓扑半金属（TSM）与平庸材料中的取值；竖线标记了支持拓扑半金属的新兴描述符的取值范围。

g 包含新元素特异性描述符 χ sq \chi_{\text{sq}} χsq的周期表：采用面心立方（fcc）配色（从最低值到最高值由蓝到红）；面板f中，数值在8到11之间的条目（白字）是拓扑半金属的代表元素。红线代表经典津特耳线，蓝框元素是已知能形成津特耳离子的元素（如Slabon⁴⁴所述）。

📌 2 适用于元素周期表的通用图深度学习原子间势

A universal graph deep learning interatomic potential for the periodic table nature computational science

主要贡献

✅1）开发了一个通用的原子间势能函数（Universal IAP）------M3GNet

论文提出了一个基于图神经网络的通用原子间势函数模型 ，称为 M3GNet（Many‑body 3‑body Graph Network） ，它能够

✅ 覆盖周期表中绝大多数元素（89种元素）

✅ 对不同材料体系进行准确的能量、力和应力预测

该势函数可用于机器学习驱动的材料模拟，如晶体结构弛豫、分子动力学、热力学性质计算等。([Nature][1])

✅ 2）通用性：覆盖周期表中的绝大多数元素

M3GNet 是目前最全面的通用 IAP 之一，它不再只针对某一类材料，而是可以处理 89种元素组合与其化合物系统 。

这意味着可以用一个模型同时模拟金属、半导体、陶瓷等材料，而不需要为每种化学体系额外训练不同势函数。

✅ 3）构建了高精度的图神经网络架构

论文的模型结合了

✔ 图神经网络（GNN）结构（节点代表原子，边代表邻接信息）

✔ 引入了 三体相互作用特征（many‑body/three‑body）

传统 GNN 只能表达 pairwise 信息，但三体信息让势能预测更接近真实物理行为（连续能量、力和应力）。([MatGL][2])

✅ 4）. 利用大规模 DFT 数据库作为训练集

模型训练使用了 Materials Project 提供的高通量 DFT 计算数据，包括：

📊 ~~187,000+ 个结构的能量

📊 ~16,000,000 种力

📊 ~1,600,000 种应力

这些大规模高质量数据是模型能够精准的关键基础。([materialsvirtuallab.org][3])

✅ 5）. 同时预测能量、力、应力，并能直接反向求力（自动求导）

通过对能量进行自回传自动求导（auto‑diff），模型可以：

✔ 算出各原子的力

✔ 得到应力张量

从而可以用于分子动力学与材料稳定性模拟，这在大多数 MLIP 中是很难兼顾的。([materialsvirtuallab.org][3])

✅ 6）. 大规模材料发现与筛选

利用这个势函数，作者对 ~31 M（百万）假设结构 进行了筛选，识别了 ~1.8 M 个潜在稳定材料 ，

并通过 DFT 验证了其中 约1578种稳定结构，展示了这套模型在大规模材料发现中的应用潜力。([arXiv][4])

摘要

原子间势（IAP）用于描述原子的势能面，是原子尺度模拟的基础输入。然而，现有原子间势要么仅适配窄范围化学体系，要么在通用场景下精度不足。本文报道了一种基于图神经网络（M3GNet）的通用原子间势，可覆盖元素周期表中的多体相互作用。

M3GNet势以"材料项目"近十年积累的大规模结构弛豫数据集为训练基础，可广泛应用于不同化学空间材料的结构弛豫、动力学模拟与性质预测。研究从3100万种假设晶体结构中，筛选出约180万种基于M3GNet能量判定的潜在稳定结构；对能量最低的2000种结构，通过密度泛函理论验证后，1578种被确认为稳定。该结果证明：机器学习加速了"可合成材料"的发现路径，助力挖掘具备目标性质的新材料。

正文

原子尺度模拟是计算机辅助材料设计的基石。多数材料计算研究的第一步是获取平衡结构，这需要在势能面（PES）中搜索极小值------涉及遍历独立晶格、原子自由度，以寻找能量最小值。原子尺度模拟也被用于研究材料体系的动力学演化（如预测热力学平均性质），例如通过分子动力学模拟获得材料的热导率、熔点等性质¹。

尽管从头算方法（如密度泛函理论，DFT）能最精准地描述势能面，但其计算成本极高：不仅难以扩展到大规模材料研究，对体系尺寸的适配性也很差。因此，线性标度的原子间势（IAP） 常被用于描述势能面。这类势函数多以"对势"形式表示原子间相互作用，但多数只能适配单一元素，或至多覆盖2--5种元素的窄范围化学体系。

目前最流行的通用势场是AMBER力场²：它最初为分子/晶体体系设计，但主要支持分子模拟，在晶体体系中的精度与适用性有限。近年来，势能面的机器学习成为原子间势开发的极具前景的方法³⁻⁵。这类"机器学习原子间势（ML-IAP）"通常将势能面表示为局部环境描述符（如原子间距、键角、原子密度）的函数，已被证明在广泛化学体系中显著优于经典原子间势。

然而，此前的图深度学习模型⁶⁻⁸虽能实现高精度预测，却未验证其对元素周期表所有化学体系的普适性。因此，目前尚无适用于任意晶体结构的通用原子间势。

过去十年，高通量自动化框架⁹⁻¹⁰的出现，推动了可靠电子结构数据（包括"材料项目"¹¹、Open Quantum Materials Database¹²、Computational Materials Repository¹³等）的发展。这些数据库的核心是"结构弛豫计算"：即通过电子结构计算得到平衡结构、能量、能带结构及衍生材料性质，用于材料筛选与设计。材料项目积累的海量"结构弛豫数据"（即中间结构及其对应能量、力与应力），为原子间势开发提供了基础。

方法与结果

本文提出一种图基深度学习原子间势 ，融合了传统原子间势的多体特征与灵活的图材料表示。利用"材料项目"自2011年成立以来积累的187000次弛豫、1600万条力、160万条应力的未开发数据集，我们训练了覆盖元素周期表89种元素的通用原子间势（M3GNet），可描述三体及多体相互作用。

M3GNet的应用场景包括声子与弹性计算、结构弛豫等；我们进一步弛豫了3000万种假设结构，以助力新材料发现。

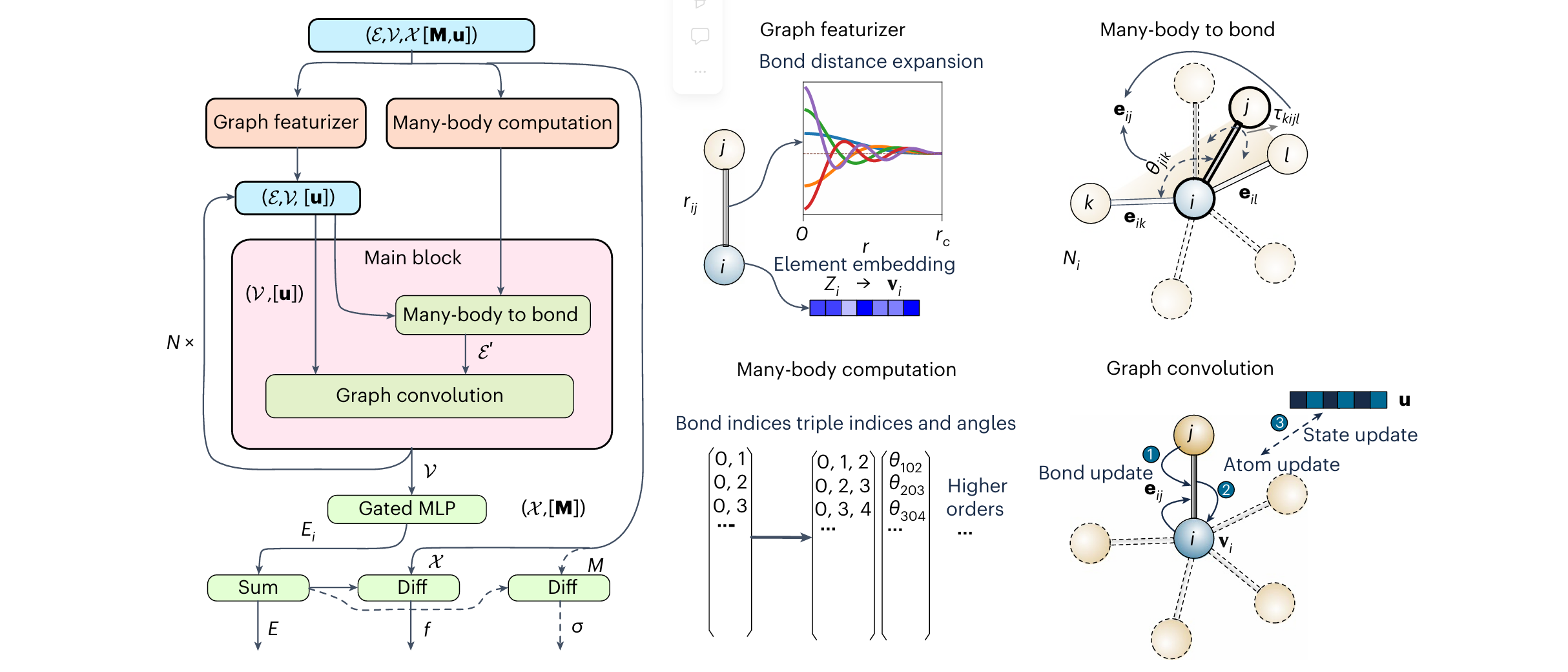
图1 多体图势与主要计算模块的示意图

模型架构始于包含原子与键的图，随后通过能量、力、应力输出的特征化与计算过程。主要模块包含图特征提取器与多体计算模块：

图特征提取器：将原子序数与元素嵌入可学习的连续特征空间；将键扩展为基函数，计算至多二阶的数值与导数（边界处设为0）。
多体计算模块：计算三体及多体相互作用的原子索引，以及原子间键的多体信息。

标准图卷积模块包含两个主要步骤：多体成键步骤与标准图卷积步骤。多体成键步骤通过考虑全键合环境 （如键角 θ i − j − l \theta_{i-j-l} θi−j−l、二面角 γ i − j − l − k \gamma_{i-j-l-k} γi−j−l−k等，以及键长 r i − j r_{i-j} ri−j等），计算原子 i i i的新键信息 Y i Y_i Yi；标准图卷积则迭代更新键与原子信息。

在聚合阶段，原子信息被传递至门控多层感知器（MLP）以获取原子能量，求和得到总能量；总能量的导数即为力与应力输出。

含多体相互作用的材料图

数学图是晶体与分子的天然表示方式：节点代表原子，边代表原子间的化学键²¹⁻²²。传统图神经网络模型在材料性质预测中表现优异²³⁻²⁴，但作为通用原子间势的效果有限------核心问题是缺乏"能量与力随键数变化的连续性"等物理约束。

本文开发了显式融合多体相互作用的材料图架构 ：材料表示为 G = { V , E , T , U , [ M ] } \mathcal{G} = \{ \mathcal{V}, \mathcal{E}, \mathcal{T}, \mathbf{U}, [\mathbf{M}] \} G={V,E,T,U,[M]}，其中 V i ∈ V \mathcal{V}i \in \mathcal{V} Vi∈V是原子(i)的信息， E i − j ∈ E \mathcal{E}{i-j} \in \mathcal{E} Ei−j∈E是连接原子(i)与(j)的键的全局状态信息， T \mathcal{T} T是可选的键信息（如坐标）， U \mathbf{U} U是单元信息， [ M ] [\mathbf{M}] [M]是晶体的3×3平移矩阵。

图特征提取器将原子间距 r i − j r_{i-j} ri−j（至某截断值 r c r_c rc）嵌入基函数，并将原子序数 Z i Z_i Zi映射至元素特征空间。

模型开发借鉴了传统原子间势的思想，例如Tersoff键序势²⁵：通过原子 i i i的近邻 j j j、 l l l的所有键组合（排除 i i i和 j j j），纳入 n n n体相互作用。本文中，我们用图神经网络生成高阶相互作用（如键角、二面角），并将其与图相互作用聚合，随后将这些信息传递至标准图卷积步骤。

标准图卷积步骤可重复多次，以构建任意复杂度的图，类似此前的材料网络架构²³。本文仅聚焦三体相互作用的融合。

在原子间势拟合场景中，原子信息映射至原子能量 E i E_i Ei，求和得到总能量 E E E；总能量用于通过自动微分计算力与应力 σ \sigma σ。

M3GNet原子间势

基于M3GNet架构开发原子间势时，我们以晶体结构为输入，以对应的能量 E E E、力 f \mathbf{f} f、应力 σ \sigma σ为训练目标。模型通过自动微分生成力与应力： f = − ∂ E / ∂ x \mathbf{f} = -\partial \mathcal{E}/\partial \mathbf{x} f=−∂E/∂x（ x \mathbf{x} x为原子坐标）， σ = ∇ V ∂ E / ∂ ϵ \sigma = \nabla_V \partial \mathcal{E}/\partial \epsilon σ=∇V∂E/∂ϵ（ V V V为体积， ϵ \epsilon ϵ为应变）。

原子间势数据集基准测试

我们选取了包含元素晶体（如面心立方镍、面心立方铜、体心立方锂、体心立方钼、金刚石硅、金刚石锗）的多样化密度泛函理论数据集，以评估M3GNet的性能。

从表1可见：M3GNet原子间势显著优于 嵌入原子法（EAM）、改进型嵌入原子法（MEAM）等经典多体势；其性能也与Behler--Parinello神经网络势（NNP）、矩张量势（MTP）等基于局部环境的机器学习原子间势相当。

需注意：尽管部分机器学习原子间势的能量与力误差略低于M3GNet，但它们在处理多元素化学体系时灵活性大幅下降------因为多元素适配会导致回归系数的组合爆炸，对数据量的需求也急剧增加。

相比之下，M3GNet架构将每个原子（节点）的元素信息表示为可学习的嵌入向量，因此能自然适配多元素化学体系。例如，针对6种元素训练的M3GNet-all势，性能与单独针对每种元素训练的M3GNet势相当。

与其他图神经网络模型类似，M3GNet无需增大键构造的截断半径即可捕捉长程相互作用（补充图1）；同时，与此前的图神经网络模型不同，M3GNet架构能保持"能量、力、应力随键数变化的连续性"------这是原子间势的关键要求（补充图2）。

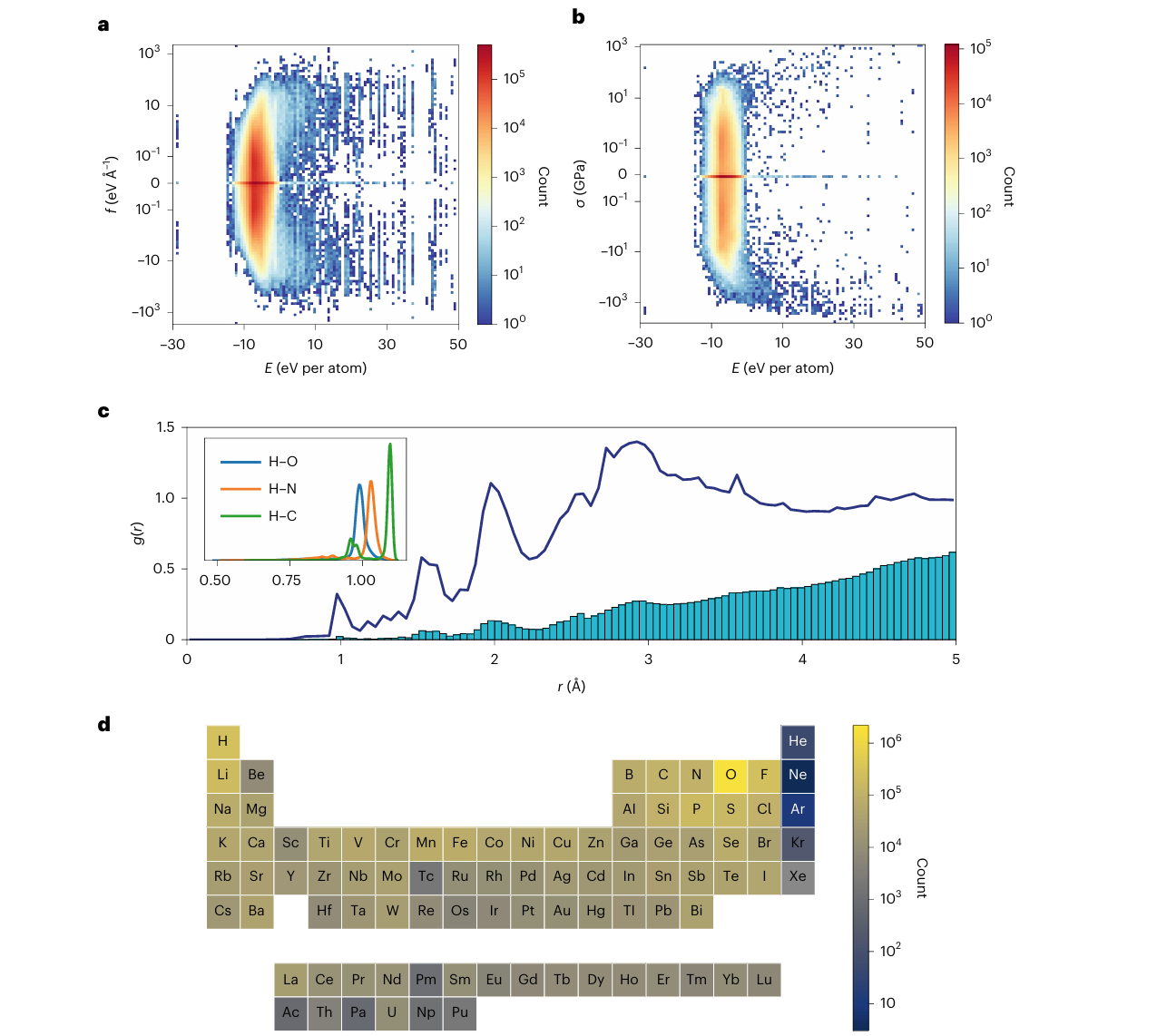
图2 | MPF.2021.2.8数据集的分布

a、b，单原子结构能（ E E E）与力（a）、应力（b）分量的分布关系。

c，径向分布函数 g ( r ) g(r) g(r)（深蓝色线）与原子对间距分布密度（浅蓝色直方图）；短间距（<1.1 Å）的密度由主要与氧、碳、氮形成氢键的原子构成，如插图所示。

d，数据集中所有原子的元素计数，覆盖了元素周期表中的89种元素。

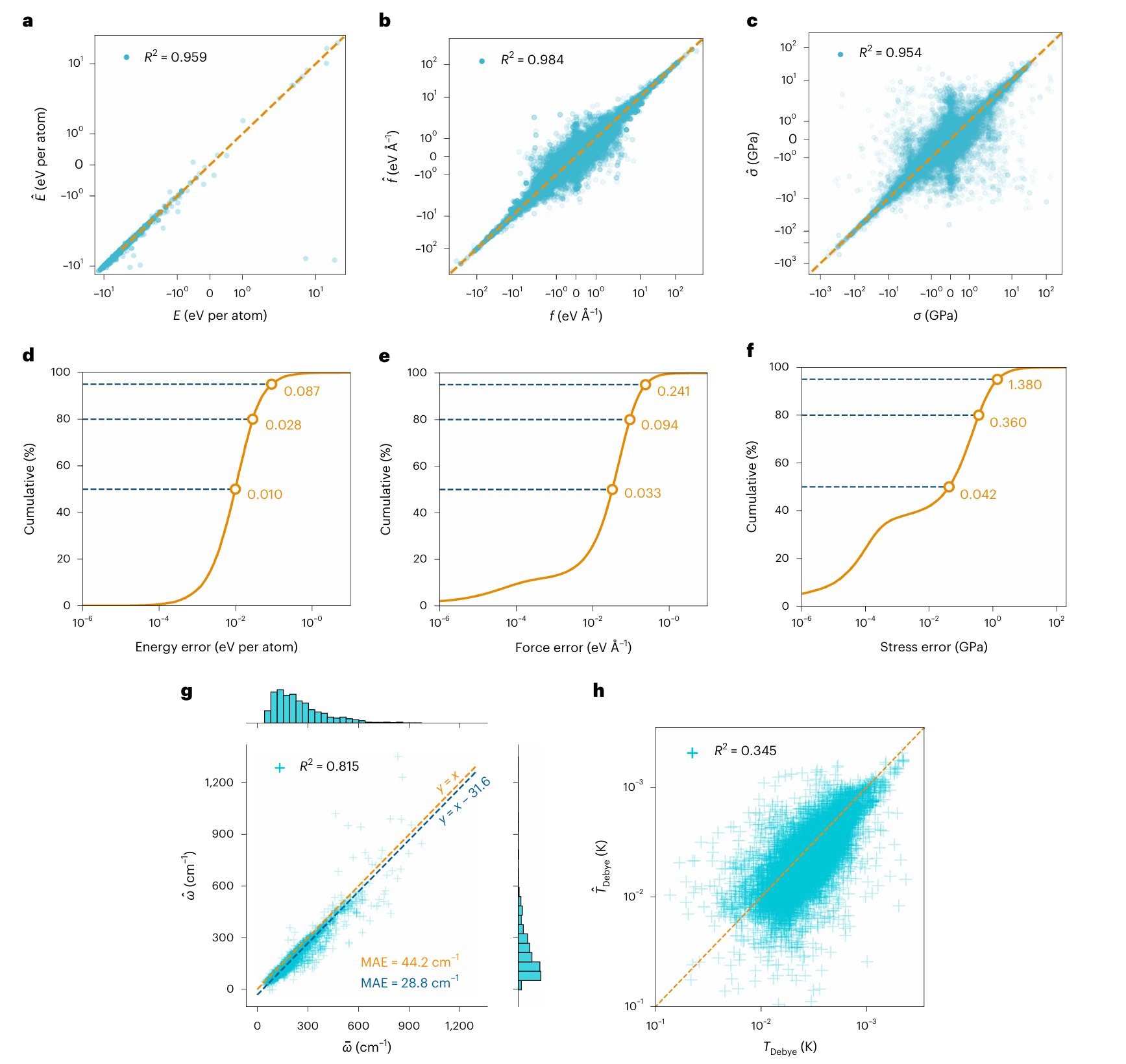
图3 | 测试数据集上的模型预测结果与DFT计算的对比

a--c，能量（ a a a）、力（ b b b）和应力（ c c c）的一致性图。模型预测结果记为 E ^ \hat{E} E^、 f ^ \hat{\mathbf{f}} f^和 σ ^ \hat{\boxed{\sigma}} σ^；虚线（ y = x y = x y=x）为参考线。

d--f，能量（ d d d）、力（ e e e）和应力（ f f f）的误差累积分布；水平虚线分别对应模型在50%、80%和95%处的误差（从下到上）。

g，模型计算的1521个声子态密度中心数据（ ω ^ \hat{\omega} ω^），与Petretto及其合作者²⁹的PBEsol DFT计算结果（ ω \omega ω）的对比。

h，由M3GNet模型得到的11848个德拜温度（排除负模量）（ Θ ^ Debye \hat{\Theta}_{\text{Debye}} Θ^Debye），与de Jong等人⁶⁴基于PBE DFT弹性张量的计算结果的对比。

📌3.利用少样本机器学习实现电子显微镜数据的快速灵活分割

Rapid and flexible segmentation of electron microscopy data using few-shot machine learning npj computational materials

这篇论文 "Rapid and flexible segmentation of electron microscopy data using few‑shot machine learning" （发表在 npj Computational Materials 2021）提出了一种能够在仅需极少标注样本（few‑shot）的情况下，对扫描透射电子显微镜（STEM）图像 进行快速且灵活的语义分割的方法，解决了传统显微图像分析难以泛化和高成本标注的问题。([Nature][1])

✅ 1）机器学习用于 STEM 图像分割

论文提出了一个 few‑shot（少样本）机器学习框架 ，用于对 STEM（扫描透射电子显微镜）图像进行 语义分割（semantic segmentation），即将图像中的不同微观区域（例如界面、相区、纳米粒子、基底背景等）自动标注出来。([Nature][1])

传统分割方法（如阈值、清洗、聚类等）

❌ 通常对噪声非常敏感

❌ 难以跨不同材料类型泛化

❌ 需要大量手工调整参数／标注数据

而本文提出的 few‑shot 方法能以 极少的标注示例（5 -- 8 个小图像片段） 即可对整张高分辨显微图像进行有效分割，大幅减少了标注工作量。([Nature][1])

✅ 2）少样本学习（Few‑Shot Learning）基本思路

传统深度学习分割需要成千上万带标签的训练样本；
Few‑shot 学习则旨在仅用少量"support set"（支持集）示例学习新类别，从而对新图像进行分类/分割。([Nature][1])

✅ 3）具体做法

划分 Chips（小图像块）

将高分辨率的 STEM 图像切成许多小的"chip"（子图像）；
构建支持集（Support Set）

从这些 chips 中，手工标注极少的示例作为每个类别的"原型（prototype）"；
利用原型网络（Prototypical Network）分类
- 每个类别的 support chips 都被映射到一个向量空间（用深度神经网络 Embedding）；
- 利用这些支持集的 embed 向量构造每个类别的 prototype；
- 将待分类的 query chip 和各类别 prototype 计算距离，进行分类；
重构分割图

将分类结果拼接成最终分割图。([Nature][2])

这种方法本质上与一般的分类任务类似，但它依赖于"距离度量而非大规模训练集"，从少数示例即可学习出特征识别能力。([Nature][2])

✅ 4）实验与表现

论文在三类典型材料的 STEM 图像上进行了验证：

SrTiO₃/Ge 外延异质结构
La₀.₈Sr₀.₂FeO₃ (LSFO) 薄膜
MoO₃ 纳米粒子

这些材料具有不同的微结构特征、形态、尺度和噪声分布。few‑shot 方法在以上数据上均展示了良好的分割效果，而且对噪声和不同对比度的图像较传统方法鲁棒性更强。([osti.gov][3])。这篇论文提出了一种基于 few‑shot machine learning 的显微图像分割方法，通过少量样例就能对复杂的 STEM 显微图像进行快速且鲁棒的语义分割，是推动高通量、智能材料表征的重要工作。

摘要

原子尺度电子显微镜图像中关键微观结构特征的自动分割，对加深理解众多重要材料、化学体系的结构-性能关系至关重要。但当前方法依赖耗时的人工分析------这类分析本质上基于经验、易出错，既无法处理现代仪器产生的海量多样化数据，也难以泛化到不同的微观结构特征与材料体系。

本文提出一种灵活的半监督少样本机器学习方法，用于扫描透射电子显微镜（STEM）图像的分割。我们以三种氧化物材料体系为验证案例：（1） S r T i O 3 （ S T O ） SrTiO₃（STO） SrTiO3（STO）/ G e Ge Ge的外延异质结构、（2） L a 0 . 8 S r 0 . 2 F e O 3 La₀.₈Sr₀.₂FeO₃ La0.8Sr0.2FeO3（ L S F O LSFO LSFO）薄膜、（3） M o O 3 MoO₃ MoO3纳米颗粒。结果表明：该少样本方法比现有方法更稳健、对噪声更不敏感，且所需的微观结构特征标注更少。此方法可实现快速图像分类，为高通量表征与自主显微镜平台赋能。

引言

材料的微观结构决定了催化剂、储能器件、量子计算等众多重要技术的功能。扫描透射电子显微镜（STEM）长期以来是研究微观结构的基础工具------它能以原子尺度分辨率解析结构、化学组成与缺陷，可表征各类材料¹⁻³。

传统上，STEM图像需人工或半自动分析：由专家先验知识指导，逐像素分类以解析不同微观结构特征⁴⁻⁵。这种方法适用于小数据量，但面对现代实验产生的海量、高噪样本时并不实用⁶⁻⁷；同时难以快速扩展，阻碍多模态数据的高通量分析，也无法与现代仪器协同⁸。更根本的是，这类方法未充分发挥测量潜力，还影响实验可重复性⁹，在复杂合金（性能受大量未知缺陷影响¹⁰⁻¹²）的分析中局限尤为突出。因此，亟需更快速、更严谨的微观结构表征方法。

定量描述显微镜图像的核心挑战，是微观结构与数据模态的多样性：同一台仪器可能先分析原子尺度界面，下一次就研究纳米颗粒或晶粒边界。在扫描电子显微镜（SEM）中，需将语义模糊的模态描述符与物理模型关联，这让精确量化特定STEM的物理意义变得困难¹³⁻¹⁴。例如，通过图像分割估算特定相的面积分数，是建立结构-性能关系的关键环节¹⁵⁻¹⁶。

尽管大津阈值法¹⁷、分水岭算法¹⁸等分割方法已被应用，但它们多针对特定体系定制，不易泛化且需大量预处理²⁰。机器学习（尤其是卷积神经网络）虽已用于微观结构识别²¹⁻²⁶，但传统深度学习需海量标注数据³³⁻³⁵，而显微镜研究中常仅能获得少量训练样本³⁸⁻³⁹。

近期研究表明，轻量级学习技术仅需少量标注即可实现自动分割³⁶·³⁷，但材料科学领域对这类方法的探索有限³⁶。少样本/单样本学习还适用于瞬态/不稳定材料（样本有限或实验周期长）的研究，也可用于分析有限的历史数据⁴³。

本文提出一种少样本机器学习方法，用于STEM图像的快速分割。我们选择三种氧化物体系（STO/Ge异质结构、LSFO薄膜、MoO₃纳米颗粒）进行验证------它们具有丰富的微观结构特征，且在半导体、自旋电子学等领域有重要应用⁴⁴⁻⁴⁵。

结果显示：仅需5--8个"子图像芯片"（特定微观结构特征的示例），模型即可得到与领域专家相当的分割结果。该方法噪声敏感性低、学习能力强，能快速识别STEM数据流中的微观结构，为实时分析提供支持，也凸显了图像驱动机器学习在高通量表征中的潜力。

结果与讨论

我们开发了一种名为"少样本学习"的深度学习方法，用于扫描透射电子显微镜（STEM）图像的超像素分割 （即对STEM图像中的超像素进行分类）。少样本学习的核心思路是：仅用少量（<10个）已标注的目标区域示例，让模型识别图像中对应类别的区域。这种半监督方法能利用材料微观结构中常见的重复模式，无需大量标注即可训练模型------甚至仅用单个标注示例，就能完成图像分割。

少样本学习实现图像分割的通用流程是：先将图像拆分为若干子图像（称为"芯片"），经模型初始化、推理后输出分割后的显微图（图1）。该方法依赖计算机视觉领域的域特定知识（如图1所示的标注技术），这类技术通常被称为"语义分割"------相比像素分类，语义分割的分类粒度更精细，但在噪声图像或像素值波动较大的场景中易出错。而少样本分割方法通过捕捉芯片中的特定微观结构特征，能更好地呈现细节；针对STEM图像的少样本纹理分割研究，也为改进微观结构表征、助力材料发现提供了可行路径。

预处理

为分离并测量STEM图像中对比度变化的不同物相，需对原始图像数据进行预处理。我们选用"限制对比度自适应直方图均衡化（CLAHE）"技术³⁹，用于增强局部图像质量；其实现细节见表1。预处理步骤为：先对原始图像执行CLAHE处理，再将处理后的图像分割为更小的子图像（图1b）。芯片尺寸在95×95像素到32×32像素之间调整------尺寸需足够大以捕捉可变结构，同时足够小以适配嵌入模块。

预处理的第二步是增强相邻空间区域的粒度（图1），通过"高斯LOG斑点检测算法"³⁹实现（该技术可同时测量特征的位置与尺寸）。我们在La₀.₈Sr₀.₂FeO₃（LSFO）体系中应用了这一步骤，以增强极微弱的相差异。

少样本模型

少样本模型输入预处理后的STEM图像（通常为高分辨率图像，约3000×3000像素），并将其拆分为若干更小的芯片（一般不超过100×100像素）。每个芯片可作为示例，或用于定义"支持集"以描述一个/多个类别。多数少样本应用会为每个类别创建独立的支持集⁵²⁻⁵⁴，因此我们将原始图像拆分为更小的子图像网格（图1b），选取其中一个子集标注为单类别，从而为每个类别定义支持集。

支持集 i i i由 N N N个标注芯片 X i = ( x i , 1 , . . . , x i , N ) X_i = (x_{i,1}, ..., x_{i,N}) Xi=(xi,1,...,xi,N)及对应"真实"类别 Y i = ( y i , 1 , . . . , y i , N ) Y_i = (y_{i,1}, ..., y_{i,N}) Yi=(yi,1,...,yi,N)组成（图1c）。

本文选择原型网络 作为相似性模块------因其轻量化设计与简洁性，可将每个支持集芯片 x i , j x_{i,j} xi,j表示为单个原型 c k c_k ck。模型通过嵌入函数 将每个芯片 x i , j x_{i,j} xi,j转换为 M M M维表示 z i , j = f θ ( x i , j ) z_{i,j} = f_\theta(x_{i,j}) zi,j=fθ(xi,j)；随后，类别 k k k的原型 c k c_k ck定义为该类别支持集嵌入表示的均值向量，公式如下：
c k = 1 N k ∑ ( x i , j , y i , j ) ∈ S k z i , j (1) c_k = \frac{1}{N_k} \sum_{(x_{i,j}, y_{i,j}) \in S_k} z_{i,j} \tag{1} ck=Nk1(xi,j,yi,j)∈Sk∑zi,j(1)

原型构建完成后，未训练的原型网络会通过以下步骤对新的查询数据进行分类：先通过嵌入函数得到查询芯片的嵌入表示，再计算其与各原型的欧氏距离，最后通过softmax归一化得到类别概率------概率最高的类别即为查询芯片的标签（图1d）。模型的最终输出是每个查询芯片对应的类别标签（图1e）。

模型推理

为了量化STEM图像中的物相分数（空间维度可达数纳米至数微米），每个芯片都会作为查询样本：嵌入后计算与各原型的距离，得到类别分布，进而分配类别。需注意：若存在未知特征，建议在支持集中新增对应的类别。

模型实现与参数

模型的具体实现与参数详见表2。尽管模型参数选择通常较为繁琐，但少样本场景下的参数设置相对简单------因为可以利用预训练的嵌入架构。本文选用**101层残差网络（ResNet101）**⁵⁸作为嵌入架构，原因是其在多个相关图像识别任务中表现优异。也可采用其他编码网络，例如更轻量化的MS-DNets³⁷、U-Nets⁵⁹，或高度专用的DefectSegNet³¹。

ResNet是一种常用模型，在多种编程语言中均可获取，且预训练权重易于迁移至STEM特定任务；ResNet101的权重来自PyTorch⁶⁰（vision v0.6.0版本），基于ImageNet⁶¹数据集训练。需说明的是：针对显微镜图像优化的网络可能提升训练与推理性能，还能支持更大批次以增强正则化。此外，我们选用欧氏距离作为度量------该度量在各类基准数据集与分类任务中普遍表现良好⁵⁷。

相似性模块也可采用其他少样本/元学习架构，但原型网络通常更简单易实现。芯片尺寸、批次大小等非模型专属参数，需结合显微图尺寸与计算内存容量确定：芯片应包含单个显微结构，具体尺寸需根据全图大小与放大倍数调试；批次大小即一次评估的芯片数量。一般来说，配备至少16GB内存、2.7GHz处理器的机器，处理64×64像素的芯片时，每0.5秒可完成1个芯片的预测，批次大小为100。计算时间还与芯片尺寸、嵌入模块的参数数量相关；若要训练少样本模型（而非本文仅讨论的推理），则至少需要1块GPU，且在大型数据集（如含1400万张图像的ImageNet⁶¹）上可能需要数天才能收敛。

分类

采用原型架构的少样本分类，在三种氧化物体系中的分割结果如图2所示。模型输出为超像素分类（即同一芯片内的所有像素共用一个标签与对应颜色），这与其他计算机视觉应用的分割方式一致⁶³。支持集类别定义了所有可能的输出类别；图2右侧展示了各支持集类别的芯片占比，通过像素尺度转换可得到每个显微图中各类别的面积占比。

STO/Ge体系对多数图像分析技术而言是个挑战------其对比度在全图范围内不规则变化，该样本是典型的薄膜-衬底界面成像数据。所选LSFO图像中，钙钛矿结构基体中存在第二相，且第二相从上到下呈梯度分布，大幅缩小了两种显微结构的细微差异；而分离这两种交织的显微结构，是理解合成过程与电导率等性能的关键。

尽管预处理可调整部分不规则性，但大津阈值法²⁰、分水岭算法²¹等传统阈值分割技术无法提供稳定结果，自适应方法在多图泛化时也会失效。另一种物相发现方法（基于滑动FFT）¹⁸虽有效，但要求图像具有周期性，且不适用于图2c所示的低倍图像------此时对比度、边缘与采样参数的卷积会增加直接解释的难度；此外，该方法也不适合分类非晶材料（非晶材料的关联序无周期性，难以局部量化）。

少样本技术也并非完全不受这些不规则性的影响（如图2a中分割后的显微图存在少量错分芯片），这些错分反映了模型对支持集选择的敏感性，这是后续研究的重要课题。总体而言，基于规范特征（分辨率高、均匀）支持集的分类，性能优于基于异常特征（含噪声、不完整）支持集的分类。

在LSFO体系中，少样本方法识别（绿色）显微结构的结果略不稳定（图2b），但这些问题可通过后处理修正（例如：对某一半径内被单一标签完全包围的芯片，调整其类别概率，或修改定义支持集的芯片）。尽管存在少量不规则性，少样本方法相比其他分割技术，对全输入图像中的噪声具有更强的鲁棒性。

此外，该少样本方法易于泛化到多种材料体系：由单张图像定义的支持集，无需调整即可应用于同类型的多张图像，大幅节省了图像序列分析的时间。这一特性在大面积映射中尤为重要（如MoO₃纳米颗粒案例）------此类场景需要采集图像拼接图，以观测各类可能的颗粒形态。

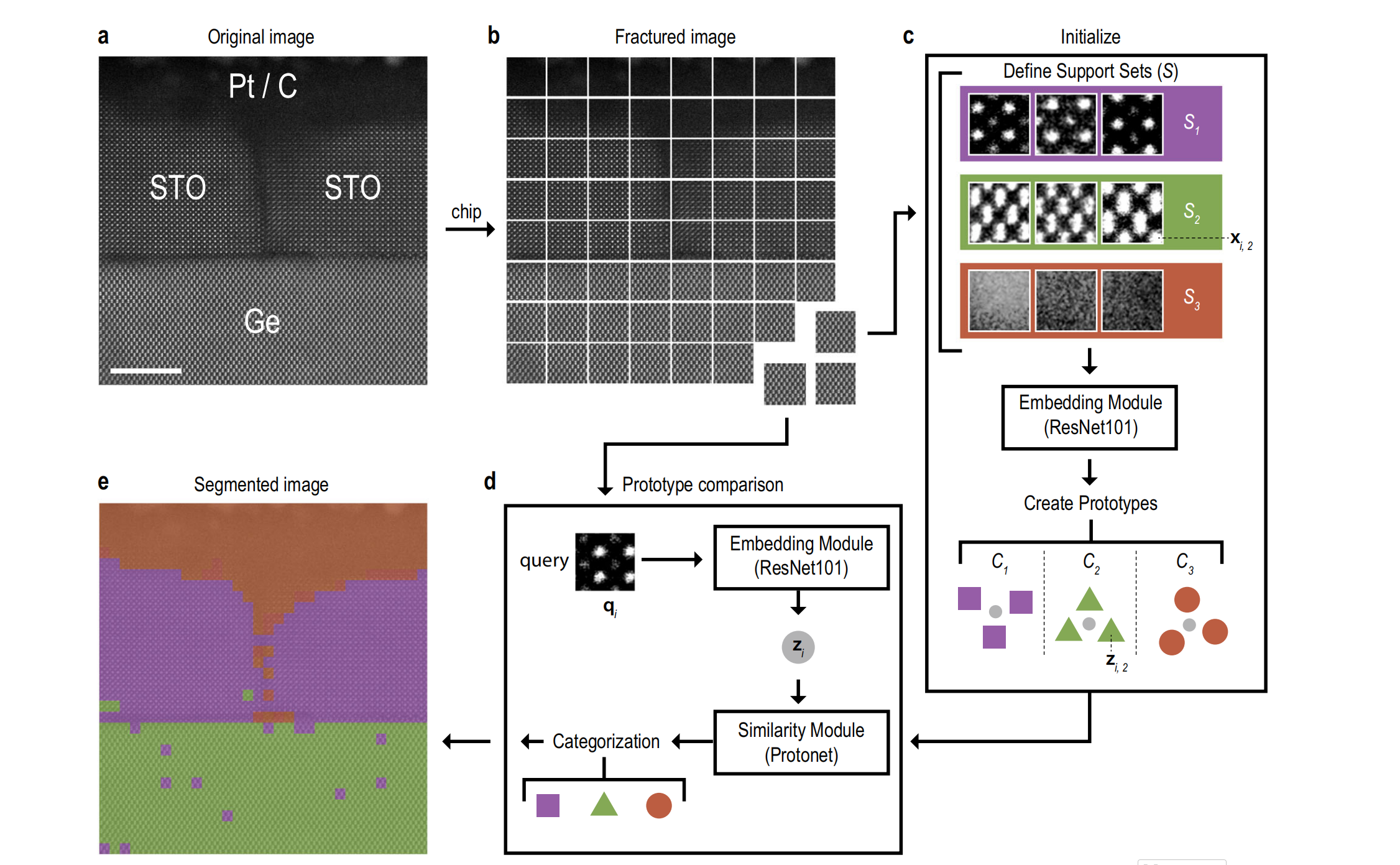
图1 少样本模型架构

原始STO/Ge图像（a）被拆分为若干子图像芯片（b）；选取少量芯片在"支持集"中代表目标分割类别（c）；每个芯片作为查询样本，与支持集定义的"原型"（d）通过欧氏距离对比分类，最终得到分割图像（e）。比例尺：5 nm。

图2 少样本分割结果

a--c 对三种材料体系（STO/Ge、LSFO、MoO₃）的分析：依次展示了原始图像（左）、对应的支持集（中），以及少样本分割的输出结果（右）；每个体系中各支持集类别的占比估算值，呈现于对应子图的插图条形图中。比例尺： a -- b a--b a--b为5 nm， c c c为5 μm。