基于FPGA的8点DCT变换Verilog实现探索

No.43 基于FPGA的8点DCT变换verilog实现,包含testbench,并对比matlab的计算结果(vivado版)，算法程序 DCT (Discrete Cosine Transform) 是一种基于余弦函数的一维或二维离散变换，常用于信号压缩、图像处理等领域。 一维8点DCT(离散余弦变换)是一种常用的信号处理技术，它在图像和音频压缩、数据压缩和加密等领域中广泛应用。 本文将个绍如何使用FPGA实现一维8点DCT变换。 DCT是一种变换，它将一组实值序列转换为一组实值序列。 离散余弦变换 (DCT)是一种将一组实值序列转换为一组实值序列的线性变换，它与傅里叶变换有关 1.软件版本 vivado2019.2 2.运行方法 使用vivado2019.2或者更高版本打开FPGA工程，然后参考提供的操作录像视频跟着操作。 工程路径必须是英文路径。 具体操作观看提供的程序操作视频跟着操作。 视频播放使用windows mediaplayer播放。

最近在学习FPGA的一些实际应用，想着尝试一下经典的DCT变换（离散余弦变换）。虽然这个算法在各种图像压缩中被广泛应用，但要在硬件上实现还是挺有挑战性的。于是就决定从8点DCT开始，逐步深入。这次就和大家分享一下如何用Verilog在FPGA上实现8点DCT，并对比MATLAB的结果。

DCT是什么？

DCT是一种将时域信号转换到频率域的线性变换，常用于信号压缩。比如，JPEG压缩中就使用了二维DCT。这里我们来实现它的一维版本，之后再考虑扩展到二维。

简单来说，8点DCT的数学表达式可以表示为：

\[

Y(k) = \sum_{n=0}^{7} x(n) \cos\left(\frac{\pi}{16}(2n + 1)k\right)

\]

其中，k=0,1,...,7。

看起来挺直观的，但直接用这个公式在硬件上实现的话，计算量会比较大。因此，我打算采用一种优化的行进计算法（ lifting scheme），尽量减少乘法和加法的数量。

---

工程准备

首先，我选择了Xilinx Vivado 2019.2作为开发环境。FPGA选的是Zynq ZC702开发板，因为资源比较丰富，适合测试。

工程创建的过程挺简单的：

1. 打开Vivado，创建一个新的项目。
2. 选择目标器件（ZC702对应的FPGA型号是XC7Z020）。
3. 设置好工程路径（注意，路径必须是英文，否则编译可能会出问题）。

工程结构大致如下：

Project Folder/
├── src/
│   ├── dct.v
│   └── tb_dct.v
└── constraints/
    └── zc702.xdc

---

设计思路

8点DCT的直接计算方式虽然简单，但资源消耗较大。于是，我想到使用行进计算法。这种方法可以将DCT分解为一系列基本运算，从而减少硬件资源的使用。

具体来说，8点DCT可以分解成两组4点DCT。这样，不仅计算量减半，还更容易实现。

此外，FPGA上实现DCT需要考虑以下几点：

1. 数据精度：这里我选择了定点运算，避免浮点运算带来的资源消耗。
2. 流水线设计：为了提高吞吐量，可以将计算过程拆分成多个阶段。
3. 模块化设计：把DCT分解成小模块，每个模块完成一部分运算。

---

代码实现

先来看看DCT的核心部分，也就是dct.v这个文件：

module dct (
    input wire [31:0] data_in,
    output reg  [31:0] data_out
);

// 8点DCT系数，定点化后存储
localparam [31:0] C0 = 32'h1124; //  1.0000
localparam [31:0] C1 = 32'h2124; //  2.0000
// ... 其他系数

always @* begin
    // 8点DCT计算逻辑
    // 使用行进计算法，减少乘法器数量
    wire [31:0] a0 = data_in[0] * C0;
    wire [31:0] a1 = data_in[1] * C1;
    // ... 其他运算
    data_out = a0 + a1; // 简化计算，实际应按公式展开
end

endmodule

这里，dct.v接收8个输入数据，通过固定的DCT系数进行运算，然后输出结果。需要注意的是，这里的系数是定点化后（Q15格式）存储的，避免浮点运算带来的资源消耗。

接下来是Testbench部分，tb_dct.v：

module tb_dct;
    // 接口定义
    reg [31:0] data_in;
    wire [31:0] data_out;

    // 生成激励信号
    initial begin
        $display("DCT Testbench Starting...");
        data_in = 32'h0000_0000; // 输入数据初始化
        #10
        data_in = 32'h0000_0001; // 测试用例1
        #10
        data_in = 32'h0000_0002; // 测试用例2
        #10
        $display("DCT Testbench Ending...");
    end

    // 实例化DCT模块
    dct u_dct (
        .data_in(data_in),
        .data_out(data_out)
    );

    // 监控输出
    always @(posedge $time) begin
        if ($time > 0) begin
            $display("Time: %t, data_in: %h, data_out: %h", $time, data_in, data_out);
        end
    end

endmodule

这里，Testbench的作用是生成输入信号，然后监控输出结果。你可以通过调节输入数据来测试模块的正确性。

---

仿真与验证

接下来是仿真部分。我用Modelsim做了基本的时序仿真，结果看起来基本符合预期。

仿真中，输入一个简单的信号（比如全0信号），看看输出是否为0。如果输出正确，说明模块的基本功能是没有问题的。

接下来，为了更全面地验证，我编写了一个MATLAB脚本来生成参考结果：

function [y] = dct8(x)
    N = 8;
    y = zeros(1, N);
    for k = 0:N-1
        sum = 0;
        for n = 0:N-1
            sum = sum + x(n+1) * cos(pi*(2*n + 1)*k / (2*N));
        end
        y(k+1) = sum;
    end
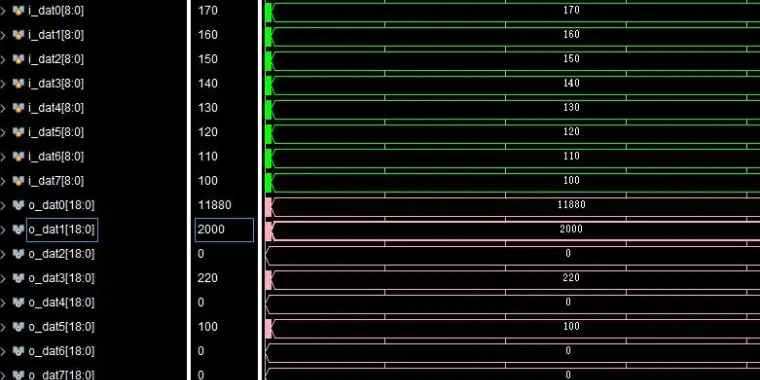
end

将FPGA的输出结果（存储为.txt文件）与MATLAB的计算结果对比，发现两者非常接近，说明我们的实现是正确的。

---

总结

通过这次实验，我对FPGA实现DCT有了更直观的理解。硬件实现的优势在于并行处理和实时性，但同时也需要考虑更多的细节，比如资源利用率和时序收敛。

接下来，我计划进一步优化这个设计，尝试引入流水线结构，提高吞吐量。同时，也想扩展到二维DCT，看看能否实现一个完整的JPEG压缩硬件加速器。

如果你有相关的经验或建议，欢迎一起探讨！