交流电机领域中的单位空间算子alpha

在看《永磁同步电机调速系统控制技术》这本书时, 遇到了 α\alphaα这个符号, 以及定子电流矢量前面的系数表示, 特此记录

单位空间算子(Space Operator)

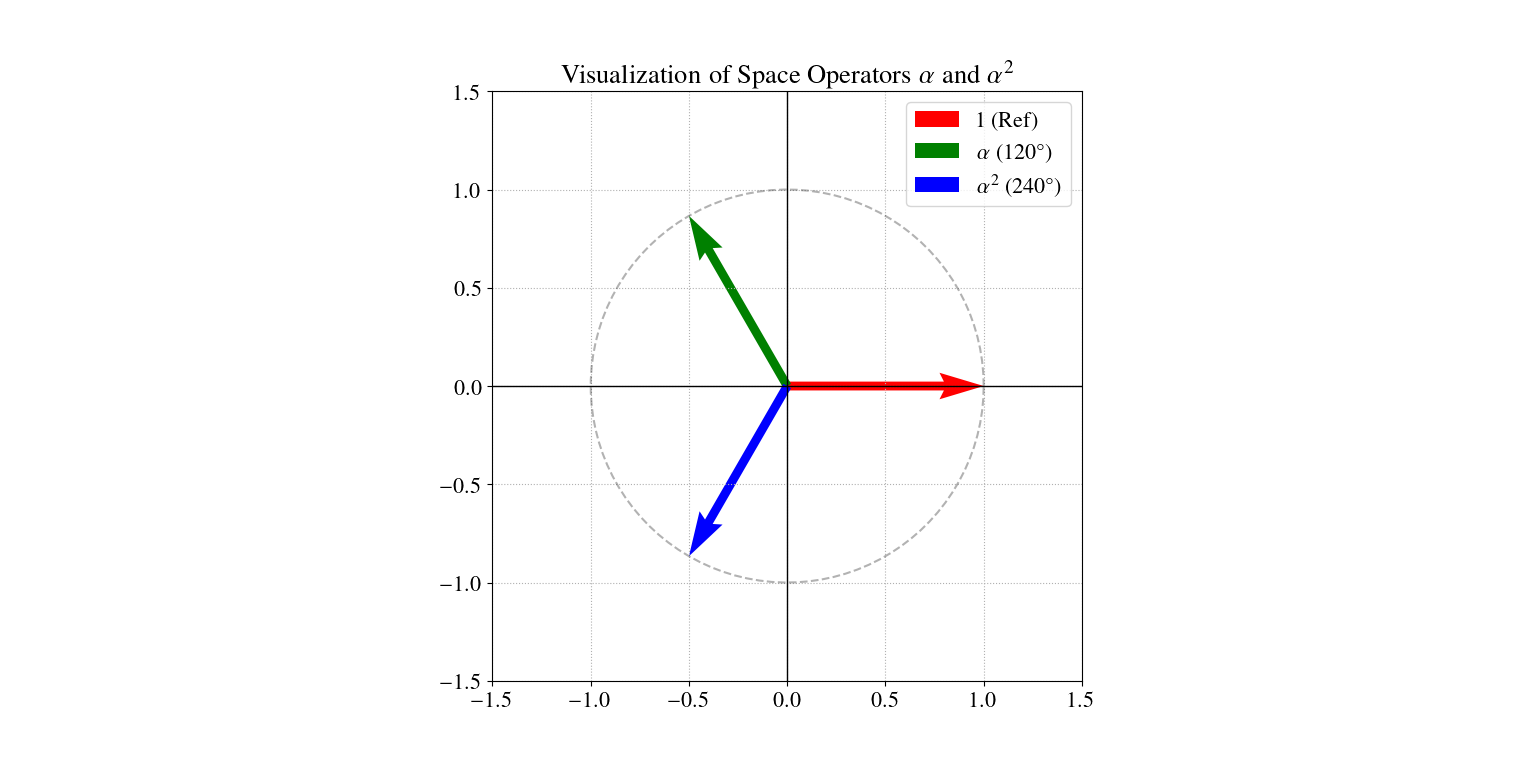
在交流电机理论中，α\alphaα 是一个单位空间算子(Space Operator)它代表在空间上逆时针旋转 120° 的单位矢量.

α=ej2π3=cos⁡(2π3)+jsin⁡(2π3)=−0.5+j32\alpha = e^{j\frac{2\pi}{3}} = \cos(\frac{2\pi}{3}) + j\sin(\frac{2\pi}{3}) = -0.5 + j\frac{\sqrt{3}}{2}α=ej32π=cos(32π)+jsin(32π)=−0.5+j23

α2=ej4π3=cos⁡(4π3)+jsin⁡(4π3)=−0.5−j32\alpha^2 = e^{j\frac{4\pi}{3}} = \cos(\frac{4\pi}{3}) + j\sin(\frac{4\pi}{3}) = -0.5 - j\frac{\sqrt{3}}{2}α2=ej34π=cos(34π)+jsin(34π)=−0.5−j23

α2\alpha^2α2 的虚部与 α\alphaα 互为相反数，即 α2=α∗\alpha^2 = \alpha^*α2=α∗(共轭复数), 在三相平衡系统中, 这种对称性保证了合成矢量的平稳旋转

三相电机的定子绕组 a,b,ca, b, ca,b,c 在物理空间上互差 120°。这个公式的作用是将三相标量电流 ia,ib,ici_a, i_b, i_cia,ib,ic 合成一个在复平面上旋转的合成矢量 isi_sis:

iai_aia 沿实轴(0°)方向;
ibi_bib 乘上 α\alphaα 意味着将其投影到 120° 方向;
ici_cic 乘上 α2\alpha^2α2 意味着将其投影到 240°(或 -120°)方向.

使用Python计算并绘制上述向量

Python 复制代码

import numpy as np
import matplotlib.pyplot as plt



# ===================== 1. 全局字体与样式配置（核心：设置Times New Roman） =====================
plt.rcParams['font.family'] = 'Times New Roman'     # 全局字体设为Times New Roman
plt.rcParams['font.size'] = 16                      # 全局基础字号
plt.rcParams['axes.unicode_minus'] = False          # 解决负号显示异常问题（关键）
# Matplotlib 默认用内置的 MathText 渲染公式, 无法直接指定 Times New Roman
# plt.rcParams['text.usetex'] = True                  # 开启LaTeX渲染(必须, 否则公式无法自定义字体)
# 适配Times New Roman的数学字体
# plt.rcParams['text.latex.preamble'] = r'\usepackage{newtxtext, newtxmath}'  

# plt.rcParams["mathtext.fontset"] = "stix"           # 'stix' 是一种非常接近 Times New Roman 的数学字体

# 开启 LaTeX 渲染
plt.rcParams.update({
    "text.usetex": True,                                            # 开启LaTeX渲染
    "font.family": "serif",                                         # 指定字体家族为"衬线字体"
    "font.serif": ["Times New Roman"],                              # 指定衬线字体列表为Times New Roman
    "text.latex.preamble": r"\usepackage{newtxtext, newtxmath}"     # 适配Times New Roman的数学字体
})


# 1. 定义算子 alpha (旋转 120 度)
# 在 Python 中, 复数单位使用 j 表示, 内置支持复数
alpha = np.exp(1j * 2 * np.pi / 3)
alpha_sq = alpha**2

# 2. 准备绘图数据
# 获取实部 (Real) 和 虚部 (Imag)
vectors = [
    (1, 0, '1 (Ref)'),
    (alpha.real, alpha.imag, r'$\alpha$ (120°)'),
    (alpha_sq.real, alpha_sq.imag, r'$\alpha^2$ (240°)')
]

# 3. 绘图
plt.figure(figsize=(6, 6))
ax = plt.gca()

# 绘制每个矢量
colors = ['r', 'g', 'b']
for i, (x, y, label) in enumerate(vectors):
    # 画箭头函数, 通过设置angles='xy'和scale=1, 确保箭头的长度和方向与坐标轴数值完全对应
    plt.quiver(0, 0, x, y, angles='xy', scale_units='xy', scale=1, 
               color=colors[i], label=label, width=0.015)

# 绘制单位圆参考线
theta = np.linspace(0, 2*np.pi, 100)
plt.plot(np.cos(theta), np.sin(theta), 'k--', alpha=0.3)

# 界面修饰
plt.axhline(0, color='black', linewidth=1)
plt.axvline(0, color='black', linewidth=1)
plt.xlim(-1.5, 1.5)
plt.ylim(-1.5, 1.5)
plt.grid(True, linestyle=':')
plt.legend()
plt.title(r'Visualization of Space Operators $\alpha$ and $\alpha^2$')
plt.gca().set_aspect('equal')
plt.show()

# 打印数值结果
print(f"alpha   = {alpha:.4f}")
print(f"alpha^2 = {alpha_sq:.4f}")