1基础搜索算法

橙汁味的风2025-12-31 10:27

模拟思维与搜索算法

第一部分：搜索问题的基本形式化

在解决问题之前，首先要定义什么是"搜索问题"。任何搜索问题都包含以下四个关键要素：

  1. 状态 ：对问题当前局面的描述（如：八数码的棋盘布局、地图上的位置）。
    • 初始状态 ( S 0 S_0 S0**)**：搜索开始的地方。
    • 目标状态 ( S g S_g Sg**)**：我们希望达到的状态，或者满足目标检测条件的集合。
  2. 动作：从一个状态转移到另一个状态的操作（如：移动滑块、移动棋子）。
  3. 路径和代价 ：
    • 路径是状态和动作的序列。
    • 耗散值：每一步动作都有代价（通常为正数），总代价是路径上所有步代价之和。
  4. 目标检测：判断当前状态是否为目标状态的函数。

教授补充知识点：

  • 状态空间 ：所有可能到达的状态的集合。搜索的本质就是在这个（通常巨大的）图上寻找一条从 S 0 S_0 S0 到 S g S_g Sg 的路径。
  • 经典案例：课件中提到了"传教士和野人问题"、"华容道"、"八皇后问题"、"地图路径规划"。复习时请在脑海中模拟这些问题是如何转化为上述四个要素的。

第二部分：盲目搜索

盲目搜索指没有关于目标具体位置的额外信息，只根据问题定义进行搜索。

1. 深度优先搜索

  • 策略：优先扩展深度最深（最近生成）的节点。

  • 实现 ：通常使用栈数据结构（后进先出 LIFO），或者使用递归。

  • 算法流程：

    1. 若当前节点是目标，返回成功。

    2. 若当前节点是死胡同，返回失败（回溯）。

    3. 生成子节点，对每一个子节点递归调用 DFS。

      lisp 复制代码 
      Depth-First-Search(DATA)
 	IF TERM(DATA) RETURN NIL;
 	IF DEADEND(DATA) RETURN FAIL;
 	RULES:=APPRULES(DATA);
	LOOP: IF NULL(RULES) RETURN FAIL;
 	 	R:=FIRST(RULES);
		RULES:=TAIL(RULES);
		RDATA:=GEN(R, DATA);
		PATH:= Depth-First-Search(RDATA);
		IF PATH=FAIL GO LOOP;
	RETURN CONS(R, PATH);

  • 优缺点：

    • 优点：节省内存（只存储当前路径上的节点）。
    • 缺点 ：
      • 死循环 ：如果是无限深度的树或有环图，可能陷入死循环（需加入Closed表或深度限制）。
      • 非最优：找到的解不一定是最短路径。

  • 变体 ：限制深度的DFS （为防止无限搜索，设定一个深度界限 BOUND）。

    lisp 复制代码 
    Depth-First-Search1(DATALIST)
 	DATA:=FIRST(DATALIST)
 	IF MEMBER(DATA, TAIL(DATALIST)) 
	 	RETURN FAIL;	
 	IF TERM(DATA) 
 		RETURN NIL;
 	IF DEADEND(DATA) 
 		RETURN FAIL;
 	IF LENGTH(DATALIST)>BOUND
	 	RETURN FAIL;
 	RULES:=APPRULES(DATA);
    LOOP: IF NULL(RULES) RETURN FAIL;
 		R:=FIRST(RULES);
		RULES:=TAIL(RULES);
		RDATA:=GEN(R, DATA);
		RDATALIST:=CONS(RDATA, DATALIST);
		PATH:= Depth-First-Search 1(RDATALIST)
		IF PATH=FAIL GO LOOP;
	RETURN CONS(R, PATH);

2. 宽度优先搜索

  • 策略：优先扩展深度最浅的节点（一层一层向外扩展）。

  • 实现 ：通常使用队列数据结构（先进先出 FIFO）。

    算法流程：

    1. 将初始节点放入 Open 表。

    2. 若 Open 表为空，失败。

    3. 取出队首节点 n n n。

    4. 若 n n n 是目标，返回成功。

    5. 扩展 n n n​，将子节点放入 Open 表队尾。

      lisp 复制代码 
      BREADTH-FIRST-SEARCH
  G:=G0(G0=s), OPEN:=(s), CLOSED:=( );
  LOOP: IF OPEN=( ) THEN EXIT (FAIL);
 	n:=FIRST(OPEN);
 	IF GOAL(n) THEN EXIT (SUCCESS);
 	REMOVE(n, OPEN), ADD(n, CLOSED);
 	EXPAND(n) →{mi}, G:=ADD(mi, G);
 	IF 目标在{mi}中 THEN EXIT(SUCCESS);
 	ADD(OPEN, m_j), 并标记m_j到n的指针;
 	GO LOOP;

  • 优缺点：

    • 优点 ：
      • 完备性：只要有解，一定能找到。
      • 最优性：当所有边的代价相等（单位代价）时，一定能找到最短路径。
    • 缺点 ：效率低，存储量极大（需存储整层的节点）。

第三部分：启发式搜索

为了提高效率，引入启发知识 来引导搜索方向，优先扩展"最有希望"的节点。

1. 核心概念：评价函数 f ( n ) f(n) f(n)

  • 定义 ：用于评估节点 n n n 的"好坏"程度。

  • 公式：

    f ( n ) = g ( n ) + h ( n ) f(n) = g(n) + h(n) f(n)=g(n)+h(n)

    • g ( n ) g(n) g(n)：从初始节点 S 0 S_0 S0 到当前节点 n n n 的实际代价（已经走过的路）。
    • h ( n ) h(n) h(n)：从当前节点 n n n 到目标节点 S g S_g Sg 的估计代价（启发函数，还未走的路）。

  • 符号含义

    • g*(n)：从s到n的最短路径的代价
    • h*(n)：从n到g的最短路径的代价
    • f*(n)=g*(n)+h*(n)：从s经过n到g的最短路径的代价
    • g(n)、h(n)、f(n)分别是g*(n)、h*(n)、f*(n)的估计值
    • 用f(n)对待扩展节点进行评价

2. A 算法

A 算法

  • 定义：使用了 f ( n ) = g ( n ) + h ( n ) f(n) = g(n) + h(n) f(n)=g(n)+h(n) 进行排序的广度优先类搜索。

  • Open 表排序 ：按 f ( n ) f(n) f(n)​ 从小到大排序，每次取最小的扩展。

    lisp 复制代码 
    A-ALGORITHM(StartNode)
    OPEN := LIST(StartNode)
    CLOSED := NIL
    G(StartNode) := 0
    F(StartNode) := G(StartNode) + H(StartNode)

    LOOP: 
        IF NULL(OPEN) RETURN FAIL;               
        
        n := FIRST(OPEN);                      
        
        IF GOAL(n) RETURN SUCCESS;             
        
        OPEN := TAIL(OPEN);                      ; 从OPEN移除 
        CLOSED := CONS(n, CLOSED);               ; 加入CLOSED 
        
        SUBNODES := EXPAND(n);              
        PROCESS-CHILDREN(SUBNODES, n);           ; 递归处理子节点
        
        SORT-BY-F-VALUE(OPEN);                
        
        GO LOOP;                         

; 辅助函数：处理 EXPAND 出来的子节点 {mi}
PROCESS-CHILDREN(NODES, n)
    IF NULL(NODES) RETURN;
    
    m := FIRST(NODES);
    REMAINING := TAIL(NODES);
    
    NEW_G := G(n) + COST(n, m);
    NEW_F := NEW_G + H(m);

    ; 情况1: m 既不在OPEN也不在CLOSED (对应 mj)
    IF (NOT MEMBER(m, OPEN)) AND (NOT MEMBER(m, CLOSED)) 
        G(m) := NEW_G;
        F(m) := NEW_F;
        POINTER(m) := n;
        OPEN := CONS(m, OPEN);

    ; 情况2: m 已经在OPEN中 (对应 mk)
    ELSE IF MEMBER(m, OPEN)
        IF NEW_F < F(m)
            G(m) := NEW_G;
            F(m) := NEW_F;
            POINTER(m) := n;
            ; 此时m已经在OPEN里，只需更新数值

    ; 情况3: m 已经在CLOSED中 (对应 ml)
    ELSE IF MEMBER(m, CLOSED)
        IF NEW_F < F(m)
            G(m) := NEW_G;
            F(m) := NEW_F;
            POINTER(m) := n;
            CLOSED := DELETE(m, CLOSED);   ; 从CLOSED中移除
            OPEN := CONS(m, OPEN);         ; 重新放回OPEN (复活)

    PROCESS-CHILDREN(REMAINING, n);        ; 递归处理下一个子节点

  • A算法详细步骤

    • 初始化与循环 (Line 1-3)

      • OPEN 表存放待检查的节点。
      • 每次循环，算法并不是像 DFS 那样取最新的，也不是像 BFS 那样取最早的，而是取 f f f 值最小的 （n:=FIRST(OPEN)，配合 Line 7 的排序）。这体现了启发式搜索的贪婪本性：总是优先尝试"看起来"最有希望的路径。

    • 扩展与分类处理 (Line 6)

      当节点 n n n 被展开，生成子节点集合 { m i } \{m_i\} {mi} 时，算法根据子节点的状态，将它们分为了三类：

      • 第一类：新节点 ( m j m_j mj)
        • 状态：以前从没见过。
        • 操作 ：计算 f , g , h f, g, h f,g,h，设指针指向 n n n，扔进 OPEN 表。
        • 含义：这是正常的地图探索。
      • 第二类：OPEN 表中的老节点 ( m k m_k mk)
        • 状态：以前见过，还没处理完（还在等待队列里）。
        • 操作 ：检查 IF f(n, mk) < f(mk)。如果现在发现经由 n n n 走到 m k m_k mk 比之前发现的路更短，那就更新 它的 f f f 值和父指针。
        • 含义 ：路径优化。就像在排队买票，突然发现另一队更快，你就换到了那个位置（更新了预期时间）。
      • 第三类：CLOSED 表中的老节点 ( m l m_l ml)
        • 状态 ：以前见过，而且已经处理完了（以为找到了到它的最短路）。
        • 操作 ：检查 IF f(n, ml) < f(ml)。
        • 动作 ：
          1. 更新 f f f 值和指针。
          2. ADD(ml, OPEN)：把它从 CLOSED 救出来，重新扔回 OPEN 表。
        • 含义 ：这是 A 算法的后悔药 。
          • 在标准的 Dijkstra 或 BFS 中，节点一旦进 CLOSED 就不再回头。
          • 但在 A 算法中，如果 h ( n ) h(n) h(n) 估价不准（导致之前的贪婪选择选错了），算法允许通过这一步来纠正错误。它承认："好吧，我之前以为那条路是最短的，我错了，现在这条路更短，我们需要以此为基础重新搜索。"

    • 排序 (Line 7)

      • OPEN中的节点按f值从小到大排序

      • 这是实现 Best-First Search 的物理手段。如果没有这一步，OPEN 就是个普通的栈或队列，算法就会退化成带有 f f f 记录的 DFS 或 BFS。

八数码问题
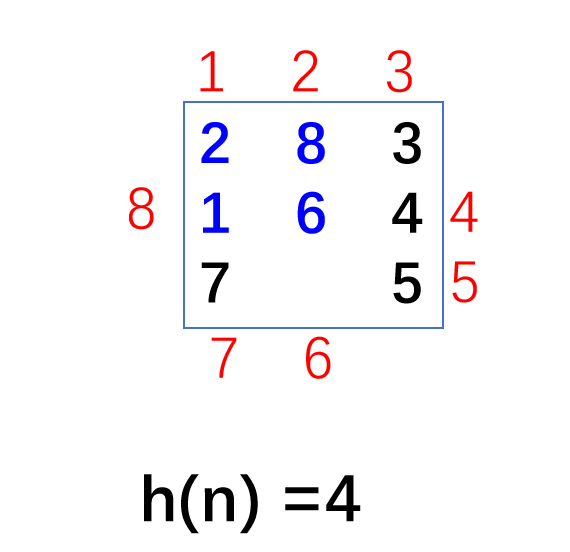
  • 在这个例子中，使用 "不在位数" 作为 h h h 函数。即有多少个数字没有在它应该在的位置上。

3. A* 算法

  • 定义 ：在 A 算法的基础上，对启发函数 h ( n ) h(n) h(n) 加以限制。

  • A 条件：

    h ( n ) ≤ h ∗ ( n ) h(n) \le h^*(n) h(n)≤h∗(n)

    • h ( n ) h(n) h(n)：我们定义的估计值。
    • h ∗ ( n ) h^*(n) h∗(n)：从 n n n 到目标的真实最小代价。
    • 解释 ：估计值必须小于等于真实值（即乐观估计）。只要满足此条件，A算法就称为A*算法。

  • 可采纳性 ：若存在从起点到终点的路径，且 h ( n ) h(n) h(n) 满足 h ( n ) ≤ h ∗ ( n ) h(n) \le h^*(n) h(n)≤h∗(n)，则 A* 算法必能找到最佳解（最短路径）。

  • 比较性质：

    • 对于同一个问题，若有两个启发函数 h 1 h_1 h1 和 h 2 h_2 h2，且都满足 A* 条件。
    • 若对于所有非目标节点，有 h 2 ( n ) > h 1 ( n ) h_2(n) > h_1(n) h2(n)>h1(n)（ h 2 h_2 h2 更接近真实值 h ∗ h^* h∗），则 A 2 A_2 A2 扩展的节点数 ≤ \le ≤ A 1 A_1 A1 扩展的节点数。
    • 结论 ：在满足可采纳性的前提下， h h h 越大越好 （越接近 h ∗ h^* h∗ 搜索效率越高）。

4. 启发函数的评价指标

  • 平均分叉数 ( b ∗ b^* b∗) ：
    • 公式： N = 1 − b ∗ ( d + 1 ) 1 − b ∗ N = \frac{1-b^{*(d+1)}}{1-b^*} N=1−b∗1−b∗(d+1) ( N N N为搜索节点总数， d d d为深度)。
    • b ∗ b^* b∗ 越小，说明启发函数效果越好 。实验表明 b ∗ b^* b∗ 通常是一个稳定的常数。

案例分析：八数码问题

  • h 1 ( n ) h_1(n) h1(n)：不在位的棋子数（较弱的启发）。
  • h 2 ( n ) h_2(n) h2(n)：所有棋子到目标位置的曼哈顿距离之和（较强的启发）。
  • 比较 ： h 2 ( n ) ≥ h 1 ( n ) h_2(n) \ge h_1(n) h2(n)≥h1(n)，且都 ≤ h ∗ ( n ) \le h^*(n) ≤h∗(n)。因此 h 2 h_2 h2 优于 h 1 h_1 h1，搜索效率更高。

第四部分：A* 算法的改进与深入

1. 单调性 与 一致性

  • 定义 ：如果启发函数 h h h 满足三角不等式：

    h ( n i ) − h ( n j ) ≤ c ( n i , n j ) h(n_i) - h(n_j) \le c(n_i, n_j) h(ni)−h(nj)≤c(ni,nj)

    其中 n j n_j nj 是 n i n_i ni 的子节点， c c c 是两点间的实际代价。同时 h ( goal ) = 0 h(\text{goal}) = 0 h(goal)=0。

  • 性质 ：若 h h h 是单调的，则 A* 算法第一次扩展 到节点 n n n 时，就已经找到了从起点到 n n n 的最佳路径 （即 g ( n ) = g ∗ ( n ) g(n) = g^*(n) g(n)=g∗(n)）。

  • 意义 ：如果满足单调性，由于第一次遇到就是最优，我们在搜索中不需要处理"重新发现同一节点但路径更短"的情况（不需要更新 Closed 表中的节点），算法效率提升。

  • 关系 ：单调性    ⟹    \implies ⟹ A* 条件（可采纳性）。大部分合理的 h h h 都是单调的（如八数码的曼哈顿距离）。

2. A* 算法的流程修正

为了避免重复扩展和保证最优性，算法流程通常包含：

  1. Open 表 ：存放待扩展节点，按 f f f 值排序。
  2. Closed 表：存放已扩展节点。
  3. 重新发现节点 ：
    • 如果新生成的子节点已经在 Open 表中：保留 g g g 值更小的那个。
    • 如果新生成的子节点已经在 Closed 表中：若新路径代价更小，将其移回 Open 表（在单调性满足时不会发生这种情况）。

八数码问题参考h(x)

1. h 1 ( n ) h_1(n) h1(n)：放错位的数码个数 (Misplaced Tiles)
  • 定义：统计当前状态中，位置与目标状态不一致的数字个数（通常忽略空位）。
  • 特点：计算最简单，但估价过于保守（Admissible but weak），搜索效率较低。
2. h 2 ( n ) h_2(n) h2(n)：曼哈顿距离 (Manhattan Distance)

  • 定义：计算每个数字从当前位置到目标位置的水平距离与垂直距离之和。

    h 2 ( n ) = ∑ t i l e ( ∣ x c u r r − x g o a l ∣ + ∣ y c u r r − y g o a l ∣ ) h_2(n) = \sum_{tile} (|x_{curr} - x_{goal}| + |y_{curr} - y_{goal}|) h2(n)=tile∑(∣xcurr−xgoal∣+∣ycurr−ygoal∣)

  • 特点 ：比 h 1 h_1 h1 更精确，是八数码问题中最常用的启发式函数。

3. h 3 ( n ) h_3(n) h3(n)：欧几里得距离 (Euclidean Distance)

  • 定义：计算每个数字当前位置与目标位置的直线距离（勾股定理）。

    h 3 ( n ) = ∑ t i l e ( x c u r r − x g o a l ) 2 + ( y c u r r − y g o a l ) 2 h_3(n) = \sum_{tile} \sqrt{(x_{curr} - x_{goal})^2 + (y_{curr} - y_{goal})^2} h3(n)=tile∑(xcurr−xgoal)2+(ycurr−ygoal)2

  • 特点：由于允许走斜线（实际上不行），它通常比曼哈顿距离小。它是可采纳的，但在这个问题中不如曼哈顿距离有效。

相关推荐
Dfreedom.2 小时前
第一阶段：U-net++的概况和核心价值
人工智能·深度学习·神经网络·计算机视觉·图像分割·u-net·u-net++
weixin_462446232 小时前
使用 Docker Compose 部署 Next-AI-Draw-IO（精简 OpenAI 兼容配置）
人工智能·docker·容器
Dfreedom.2 小时前
循阶而上，庖丁解牛：系统学习开源 AI 模型的行动指南
人工智能·深度学习·学习·开源·图像算法
亚马逊云开发者2 小时前
使用 Kiro AI IDE 开发 基于Amazon EMR 的Flink 智能监控系统实践
人工智能
数据光子2 小时前
【YOLO数据集】自动驾驶
人工智能·yolo·自动驾驶
Elastic 中国社区官方博客2 小时前
使用 Elasticsearch 中的结构化输出创建可靠的 agents
大数据·人工智能·elk·elasticsearch·搜索引擎·ai·全文检索
北京耐用通信2 小时前
告别AGV“迷路”“断联”！耐达讯自动化PROFIBUS三路中继器，用少投入解决大麻烦
人工智能·科技·网络协议·自动化·信息与通信
xinyaozixun2 小时前
闪极loomos系列AI眼镜重磅发布，重构日常佩戴体验，再次引领智能穿戴赛道
人工智能·重构
Hcoco_me2 小时前
大模型面试题22：从通俗理解交叉熵公式到通用工程实现
人工智能·rnn·自然语言处理·lstm·word2vec
热门推荐
01GitHub 镜像站点02从快手“12·22”直播攻击事件看：一次教科书式的业务层饱和攻击03Linux下V2Ray安装配置指南04Claude Code Skills 实用使用手册05UV安装并设置国内源06jdk21下载、安装（Windows、Linux、macOS）07电脑检测软件—图吧工具箱08Google Antigravity Agent 编辑器操作教程092025 最新教程：注册并切换到美区 Apple ID10【踩坑笔记】50系显卡适配的 PyTorch 安装