0 前言
最近在处理各类问题中,发现很多重要的数学概念并没有很好的理解,更没有深入了解在流体力学中,这些数学概念的物理意义。因此后续会整理系列化文章,梳理常见的数学概念。在编写时候,尽可能避免晦涩难懂的数学描述,聚焦于这些抽象的数学概念如何通过具象化的流体力学现象理解物理意义。
1 极限的定义
极限(limit)是微积分中最基础的概念。微积分后续所有概念(微分、积分、梯度、通量等)都以极限这个概念作为基础。
极限的定义为:在函数自变量接近某个特定取值或趋向于无穷大时,函数值的变化趋势。
在数学中,极限的记录符号为:
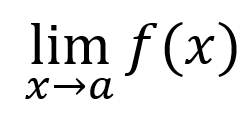
\lim_{x\rightarrow a}{f(x)}
在数学中,诸多常见简单函数的极限有现成结果,也有很多方式计算某些复杂函数的极限。常见简单函数的极限举例:
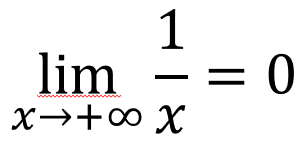
\lim_{x \to +\infty} \frac{1}{x} = 0
上述极限表示,在自变量趋向于正无穷大时,函数值将趋向于 0。
基于极限的定义,需要注意几个问题:
1 自变量是趋近于某个特定取值,但是此特定取值可能不在函数的定义域中
例如,下述极限结果,函数在 x=0 时是没有定义的。
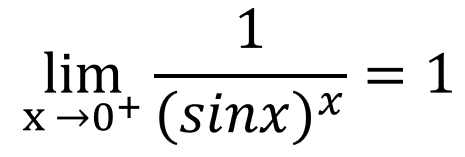
\lim_{x \rightarrow 0^+} \frac{1}{(\sin x)^x} = 1
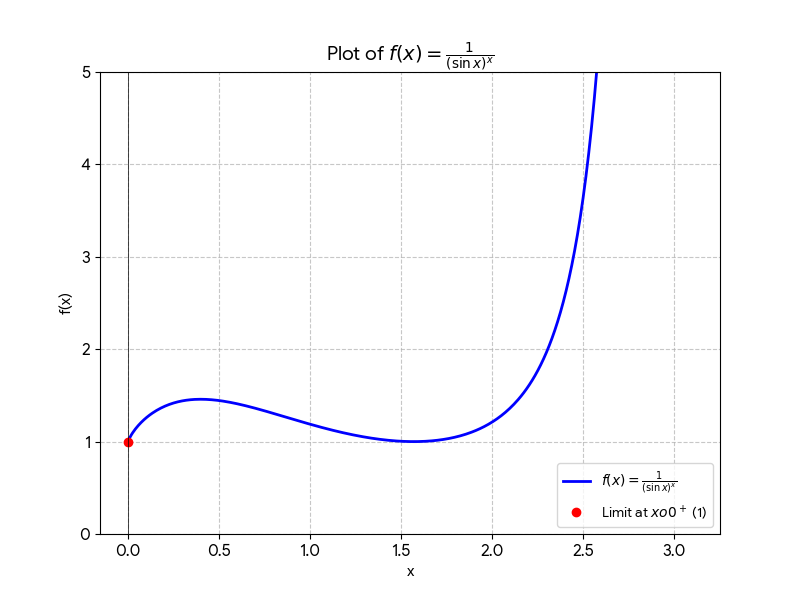
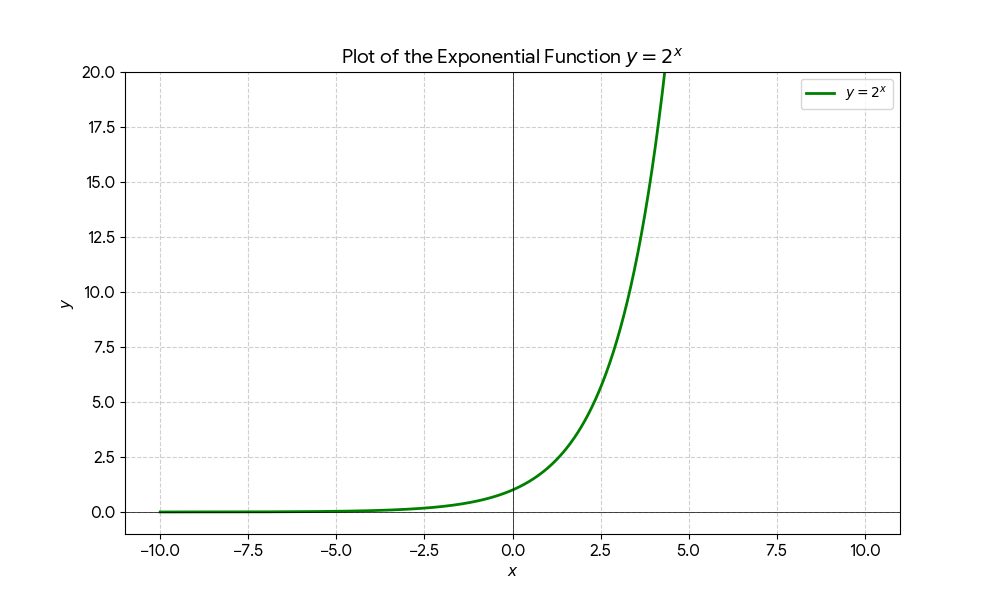
2 函数值不会达到极限的数值
例如,下述极限结果,对于任意 x 的取值,函数值始终为正数,只是随着 x 取值的变小,函数值不断向 0 靠近。
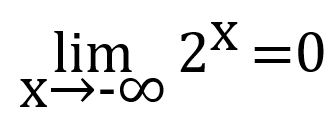
\lim_{x\rightarrow-\infty}{2^x}=0
2 极限概念在流体力学中的重要性
在流体力学中,从理论基础到实际应用始终充满极限这个基本思想。
2.1 连续介质假设
经典流体力学前提假设为流体是连续介质。基于连续介质假设,才可以定义有实际宏观意义的流场。此假设为物质无穷稠密时的极限状态,无视了物质实际是由若干离散分子组成的物理事实。
分析常见的流体力学现象,如飞机飞行、河流流动等,基于连续介质假设构建的经典流体力学是足够精确的。在高真空度等特殊环境下,连续介质假设不成立,无法使用经典流体力学相关理论分析。
连续介质假设是否成立,在流体力学中通常使用克努森数(Knudsen Number,简写为Kn)判断。
2.2 极限的其他应用实例
流体力学应用中,典型的极限问题为流场的稳态解,即经历无穷长的时间后流场的状态。真实世界中,由于各种干扰项无法完全消除,因此不存在严格的稳态流场。无论实验中如何控制外部条件,流场都只能够和稳态充分近似。
在CFD仿真中也有很多类似思想的应用。
例如在网格划分阶段,无限扩大计算域范围,且无限细化网格可使计算结果无限精确可靠。但是硬件资源是有限的,因此计算域只能做到足够大,网格只能有限的细化且主要在重点关注区域细化。