引言:从"经验值"到无限大
我对数值计算的执念,来自初中时代烟雾缭绕的网吧。那时玩《伝奇》,最让我着迷的不是打怪爆装备,而是角色面板里那条长长的经验值。看着数字不断跳动、累积,最终"叮"一声升级,那种简单的数值驱动整个世界运转的感觉,实在太奇妙了。
当时自学编程,从 G-BASIC 里只有 16 位的 INTEGER,到第一次发现 QBASIC LONG 能存下"20亿"时的兴奋,再到如今成为一名 .NET 程序员,手握理论上"无限大"的 System.Numerics.BigInteger。我对大数的迷恋从未改变,只是疑惑随之而来:
作为 .NET 开发者,我手里的
BigInteger到底够不够快?特别是和隔壁 Java 的BigInteger相比,究竟谁更胜一筹?
尤其是涉及高精度计算、密码学等关键领域时,这不仅是好奇,更是关乎性能的严肃拷问。今天,我就通过一次详尽的对比测试(含 .NET 10、Java 21以及Java 8),来为大家揭晓答案。结果可能出乎意料,请务必看到最后,文末还有一个高性能的"彩蛋"。
实验目标与范围
我们对比这三套实现:
- .NET :
System.Numerics.BigInteger(基于 .NET 10) - Java :
java.math.BigInteger- Java 21(最新LTS):代表未来趋势
- Java 8(国内存量最大):代表庞大的现状
测试操作(3类,覆盖常见大数热点)
- ADD_MOD :
(a + b) mod m(加法 + 取模) - MUL_MOD :
(a * b) mod m(乘法 + 取模) - MODPOW :
a^e mod m(模幂,密码学等场景的性能热点)
位宽(3档)
- 256 / 1024 / 4096 bits
计时口径(尽量抑制噪声)
- 热身:预热 5 次,让 JIT(即时编译器)充分发挥。
- 测量:正式跑 11 次,取中位数,避免单次抖动干扰。
- 指标 :
nsPerOp(每次操作耗时多少纳秒),这个值越小越好。 - 防作弊 :用
XOR聚合每次计算结果,防止聪明的编译器把整个循环优化掉。
测试环境
说明:以下是在同一 Linux 容器内完成。容器有资源限制,因此"看到的 CPU 核数/内存"与宿主机不完全一致。
- OS:Ubuntu 24.04.3 LTS
- CPU(宿主机型号) :AMD EPYC 7763 64-Core Processor
容器可用核心数:2 核(受容器限制) - 内存:2GB(容器限制)
- .NET
- SDK:10.0.101
- Runtime:10.0.1
- 环境变量:
DOTNET_GCServer=1
- Java
- Java 21:OpenJDK 21.0.9(LTS)
- Java 8:Temurin(OpenJDK) 1.8.0_472-b08(广泛使用的 8u 系列)
- JVM 参数(两版本一致):
-Xms1g -Xmx1g(把 Java 堆固定为 1GB,避免堆动态扩张干扰)-XX:+UseG1GC-XX:+AlwaysPreTouch(尽量减少运行中页分配扰动)
- 一致性约束
- Java 8/Java 21 使用同一份源码 (仅使用 Java 8 语法),并且 用 Java 8 的
javac编译(classfile=52.0)后分别在 Java 8 / Java 21 上运行,从而尽量把差异归因到运行时/JIT/库实现,而不是编译器生成差异。
- Java 8/Java 21 使用同一份源码 (仅使用 Java 8 语法),并且 用 Java 8 的
赛前插曲:.NET BigInteger 真的"不公平"吗?
有人可能想问:
".NET BigInteger 每次运算都会创建新的对象(不可变),不公平。"
这句话在"大数场景"里基本成立,但Java BigInteger 同样是不可变类型 :add/multiply/mod/xor/modPow 都会返回新值,业务代码层面你并没有公开的 in-place API 可以复用内部缓冲。
因此,在本文的"主对比"(.NET vs Java)里,双方都在不可变范式下运行,这点是公平的。
实验一:.NET BigInteger vs Java 21 BigInteger
3.1 完整源代码
Java 源码:BigIntBench.java
兼容 Java 8 语法;同一份代码在 Java 21 下运行。
java
import java.math.BigInteger;
import java.util.*;
public class BigIntBench {
// SplitMix64 RNG (deterministic, fast)
static final class SplitMix64 {
private long x;
SplitMix64(long seed) { this.x = seed; }
long nextLong() {
long z = (x += 0x9E3779B97F4A7C15L);
z = (z ^ (z >>> 30)) * 0xBF58476D1CE4E5B9L;
z = (z ^ (z >>> 27)) * 0x94D049BB133111EBL;
return z ^ (z >>> 31);
}
void nextBytes(byte[] dst) {
int i = 0;
while (i < dst.length) {
long v = nextLong();
for (int k = 0; k < 8 && i < dst.length; k++) {
dst[i++] = (byte)(v >>> (56 - 8*k)); // big-endian stream
}
}
}
}
static BigInteger[] genBigInts(int bitSize, int count, long seed) {
SplitMix64 rng = new SplitMix64(seed);
int byteLen = (bitSize + 7) / 8;
BigInteger[] arr = new BigInteger[count];
byte[] buf = new byte[byteLen];
int topBit = (bitSize - 1) % 8;
int keepBits = topBit + 1;
int firstMask = (keepBits == 8) ? 0xFF : ((1 << keepBits) - 1);
byte topMask = (byte)(1 << topBit);
for (int i = 0; i < count; i++) {
rng.nextBytes(buf);
// Ensure exact bit length:
// - mask away unused top bits when bitSize is not byte-aligned
// - set the top bit so the number has the requested bit length
buf[0] &= (byte)firstMask;
buf[0] |= topMask;
arr[i] = new BigInteger(1, buf);
}
return arr;
}
static BigInteger genModulus(int bitSize, long seed) {
SplitMix64 rng = new SplitMix64(seed);
int byteLen = (bitSize + 7) / 8;
byte[] buf = new byte[byteLen];
rng.nextBytes(buf);
int topBit = (bitSize - 1) % 8;
int keepBits = topBit + 1;
int firstMask = (keepBits == 8) ? 0xFF : ((1 << keepBits) - 1);
buf[0] &= (byte)firstMask;
buf[0] |= (byte)(1 << topBit);
buf[buf.length - 1] |= 1; // odd
return new BigInteger(1, buf);
}
enum Op { ADD_MOD, MUL_MOD, MODPOW }
static final class Result {
final String lang;
final int bits;
final Op op;
final long ops;
final double nsPerOp;
final long checksum;
Result(String lang, int bits, Op op, long ops, double nsPerOp, long checksum) {
this.lang = lang; this.bits = bits; this.op = op; this.ops = ops; this.nsPerOp = nsPerOp; this.checksum = checksum;
}
String toJson() {
return String.format(Locale.ROOT,
"{\"lang\":\"%s\",\"bits\":%d,\"op\":\"%s\",\"ops\":%d,\"nsPerOp\":%.3f,\"checksum\":%d}",
lang, bits, op.name(), ops, nsPerOp, checksum);
}
}
static long runOnce(Op op, BigInteger[] a, BigInteger[] b, BigInteger[] e, BigInteger mod, int outer) {
BigInteger acc = BigInteger.ZERO;
int n = a.length;
switch (op) {
case ADD_MOD:
for (int o = 0; o < outer; o++) {
for (int i = 0; i < n; i++) {
BigInteger r = a[i].add(b[i]).mod(mod);
acc = acc.xor(r);
}
}
break;
case MUL_MOD:
for (int o = 0; o < outer; o++) {
for (int i = 0; i < n; i++) {
BigInteger r = a[i].multiply(b[i]).mod(mod);
acc = acc.xor(r);
}
}
break;
case MODPOW:
// here we use a.length as n; e can be same length
for (int o = 0; o < outer; o++) {
for (int i = 0; i < n; i++) {
BigInteger r = a[i].modPow(e[i], mod);
acc = acc.xor(r);
}
}
break;
default:
throw new IllegalArgumentException("Unknown op: " + op);
}
return acc.longValue();
}
static Result bench(String lang, int bits, Op op, BigInteger[] a, BigInteger[] b, BigInteger[] e, BigInteger mod, long targetOps, int warmups, int measures) {
int n = a.length;
int outer = (int)Math.max(1, targetOps / n);
long actualOps = (long)n * outer;
// warmup
long ck = 0;
for (int i = 0; i < warmups; i++) {
ck ^= runOnce(op, a, b, e, mod, outer);
}
long[] times = new long[measures];
for (int i = 0; i < measures; i++) {
long t0 = System.nanoTime();
long c = runOnce(op, a, b, e, mod, outer);
long t1 = System.nanoTime();
ck ^= c;
times[i] = (t1 - t0);
}
Arrays.sort(times);
long median = times[times.length / 2];
double nsPerOp = (double)median / (double)actualOps;
return new Result(lang, bits, op, actualOps, nsPerOp, ck);
}
static void printHuman(List<Result> results) {
System.out.println("Java BigInteger benchmark");
System.out.println("java.version=" + System.getProperty("java.version"));
System.out.println("java.vm.name=" + System.getProperty("java.vm.name"));
System.out.println();
System.out.printf(Locale.ROOT, "%-6s %-9s %-12s %-12s\n", "Bits", "Op", "ns/op(med)", "ops/run");
for (Result r : results) {
System.out.printf(Locale.ROOT, "%-6d %-9s %-12.3f %-12d\n", r.bits, r.op.name(), r.nsPerOp, r.ops);
}
System.out.println();
System.out.println("checksum=" + results.stream().mapToLong(x -> x.checksum).reduce(0L, (x,y)->x^y));
}
public static void main(String[] args) {
boolean json = false;
for (String a : args) if (a.equals("--json")) json = true;
int warmups = 5;
int measures = 11;
int[] bitSizes = new int[]{256, 1024, 4096};
List<Result> results = new ArrayList<>();
for (int bits : bitSizes) {
BigInteger mod = genModulus(bits, 0xA1B2C3D4E5F60708L ^ bits);
// add/mul datasets
int nAddMul = 1024;
BigInteger[] a = genBigInts(bits, nAddMul, 0x1111222233334444L ^ bits);
BigInteger[] b = genBigInts(bits, nAddMul, 0x9999AAAABBBBCCCCL ^ bits);
// modpow datasets (smaller)
int nPow = 256;
BigInteger[] ap = genBigInts(bits, nPow, 0x13579BDF2468ACE0L ^ bits);
BigInteger[] ep = genBigInts(Math.min(bits, 512), nPow, 0x0FEDCBA987654321L ^ bits);
long addOps;
long mulOps;
long powOps;
if (bits == 256) {
addOps = 2_000_000L;
mulOps = 500_000L;
powOps = 8_000L;
} else if (bits == 1024) {
addOps = 1_000_000L;
mulOps = 120_000L;
powOps = 1_500L;
} else {
addOps = 200_000L;
mulOps = 20_000L;
powOps = 250L;
}
results.add(bench("java", bits, Op.ADD_MOD, a, b, null, mod, addOps, warmups, measures));
results.add(bench("java", bits, Op.MUL_MOD, a, b, null, mod, mulOps, warmups, measures));
results.add(bench("java", bits, Op.MODPOW, ap, null, ep, mod, powOps, warmups, measures));
}
if (json) {
for (Result r : results) System.out.println(r.toJson());
} else {
printHuman(results);
}
}
}.NET 源码:Program.cs(BigInteger 部分)
这是"主对比"用的 .NET 基准程序。
csharp
using System;
using System.Collections.Generic;
using System.Diagnostics;
using System.Globalization;
using System.Linq;
using System.Numerics;
sealed class SplitMix64
{
private ulong _x;
public SplitMix64(ulong seed) => _x = seed;
public ulong NextUInt64()
{
ulong z = (_x += 0x9E3779B97F4A7C15UL);
z = (z ^ (z >> 30)) * 0xBF58476D1CE4E5B9UL;
z = (z ^ (z >> 27)) * 0x94D049BB133111EBUL;
return z ^ (z >> 31);
}
public void NextBytes(byte[] dst)
{
int i = 0;
while (i < dst.Length)
{
ulong v = NextUInt64();
for (int k = 0; k < 8 && i < dst.Length; k++)
{
dst[i++] = (byte)(v >> (56 - 8 * k)); // big-endian stream
}
}
}
}
enum Op { ADD_MOD, MUL_MOD, MODPOW }
record Result(string Lang, int Bits, Op Op, long Ops, double NsPerOp, long Checksum)
{
public string ToJson() => string.Create(CultureInfo.InvariantCulture,
$"{{\"lang\":\"{Lang}\",\"bits\":{Bits},\"op\":\"{Op}\",\"ops\":{Ops},\"nsPerOp\":{NsPerOp:F3},\"checksum\":{Checksum}}}");
}
static class BigIntBench
{
static BigInteger[] GenBigInts(int bitSize, int count, ulong seed)
{
var rng = new SplitMix64(seed);
int byteLen = (bitSize + 7) / 8;
var arr = new BigInteger[count];
var buf = new byte[byteLen];
int topBit = (bitSize - 1) % 8;
byte topMask = (byte)(1 << topBit);
for (int i = 0; i < count; i++)
{
rng.NextBytes(buf);
buf[0] |= topMask;
// unsigned + big-endian prevents negative
arr[i] = new BigInteger(buf, isUnsigned: true, isBigEndian: true);
}
return arr;
}
static BigInteger GenModulus(int bitSize, ulong seed)
{
var rng = new SplitMix64(seed);
int byteLen = (bitSize + 7) / 8;
var buf = new byte[byteLen];
rng.NextBytes(buf);
int topBit = (bitSize - 1) % 8;
buf[0] |= (byte)(1 << topBit);
buf[^1] |= 1; // odd
return new BigInteger(buf, isUnsigned: true, isBigEndian: true);
}
static long RunOnce(Op op, BigInteger[] a, BigInteger[] b, BigInteger[] e, BigInteger mod, int outer)
{
BigInteger acc = BigInteger.Zero;
int n = a.Length;
switch (op)
{
case Op.ADD_MOD:
for (int o = 0; o < outer; o++)
for (int i = 0; i < n; i++)
{
var r = (a[i] + b[i]) % mod;
acc ^= r;
}
break;
case Op.MUL_MOD:
for (int o = 0; o < outer; o++)
for (int i = 0; i < n; i++)
{
var r = (a[i] * b[i]) % mod;
acc ^= r;
}
break;
case Op.MODPOW:
for (int o = 0; o < outer; o++)
for (int i = 0; i < n; i++)
{
var r = BigInteger.ModPow(a[i], e[i], mod);
acc ^= r;
}
break;
}
return (long)(acc & long.MaxValue); // stable checksum
}
static Result Bench(string lang, int bits, Op op, BigInteger[] a, BigInteger[] b, BigInteger[] e, BigInteger mod, long targetOps, int warmups, int measures)
{
int n = a.Length;
int outer = (int)Math.Max(1, targetOps / n);
long actualOps = (long)n * outer;
long ck = 0;
for (int i = 0; i < warmups; i++)
ck ^= RunOnce(op, a, b, e, mod, outer);
long[] timesNs = new long[measures];
for (int i = 0; i < measures; i++)
{
var sw = Stopwatch.StartNew();
long c = RunOnce(op, a, b, e, mod, outer);
sw.Stop();
ck ^= c;
// Stopwatch ticks to ns
timesNs[i] = (long)(sw.ElapsedTicks * (1_000_000_000.0 / Stopwatch.Frequency));
}
Array.Sort(timesNs);
long median = timesNs[timesNs.Length / 2];
double nsPerOp = (double)median / actualOps;
return new Result(lang, bits, op, actualOps, nsPerOp, ck);
}
static void PrintHuman(List<Result> results)
{
Console.WriteLine("C# BigInteger benchmark");
Console.WriteLine($"dotnet.version={Environment.Version}");
Console.WriteLine($"os={System.Runtime.InteropServices.RuntimeInformation.OSDescription}");
Console.WriteLine($"arch={System.Runtime.InteropServices.RuntimeInformation.OSArchitecture}");
Console.WriteLine();
Console.WriteLine($"{ "Bits",-6} {"Op",-9} {"ns/op(med)",-12} {"ops/run",-12}");
foreach (var r in results)
Console.WriteLine(string.Create(CultureInfo.InvariantCulture, $"{r.Bits,-6} {r.Op,-9} {r.NsPerOp,-12:F3} {r.Ops,-12}"));
Console.WriteLine();
long checksum = 0;
foreach (var r in results) checksum ^= r.Checksum;
Console.WriteLine($"checksum={checksum}");
}
public static int Main(string[] args)
{
bool json = args.Any(a => a == "--json");
int warmups = 5;
int measures = 11;
int[] bitSizes = [256, 1024, 4096];
var results = new List<Result>();
foreach (int bits in bitSizes)
{
var mod = GenModulus(bits, 0xA1B2C3D4E5F60708UL ^ (uint)bits);
int nAddMul = 1024;
var a = GenBigInts(bits, nAddMul, 0x1111222233334444UL ^ (uint)bits);
var b = GenBigInts(bits, nAddMul, 0x9999AAAABBBBCCCCUL ^ (uint)bits);
int nPow = 256;
var ap = GenBigInts(bits, nPow, 0x13579BDF2468ACE0UL ^ (uint)bits);
var ep = GenBigInts(Math.Min(bits, 512), nPow, 0x0FEDCBA987654321UL ^ (uint)bits);
long addOps = bits switch { 256 => 2_000_000L, 1024 => 1_000_000L, _ => 200_000L };
long mulOps = bits switch { 256 => 500_000L, 1024 => 120_000L, _ => 20_000L };
long powOps = bits switch { 256 => 8_000L, 1024 => 1_500L, _ => 250L };
results.Add(Bench("csharp", bits, Op.ADD_MOD, a, b, null!, mod, addOps, warmups, measures));
results.Add(Bench("csharp", bits, Op.MUL_MOD, a, b, null!, mod, mulOps, warmups, measures));
results.Add(Bench("csharp", bits, Op.MODPOW, ap, null!, ep, mod, powOps, warmups, measures));
}
if (json)
{
foreach (var r in results) Console.WriteLine(r.ToJson());
}
else
{
PrintHuman(results);
}
return 0;
}
}3.2 运行方式(可复现命令)
bash
# Java 21
cd /app/bigintbench/java
javac BigIntBench.java
java -Xms1g -Xmx1g -XX:+UseG1GC -XX:+AlwaysPreTouch BigIntBench --json
# .NET 10
cd /app/bigintbench/csharp
dotnet build -c Release
DOTNET_GCServer=1 dotnet run -c Release -- --json3.3 实验一原始输出(JSONL)
Java 21:results_java21.jsonl
jsonl
{"lang":"java","bits":256,"op":"ADD_MOD","ops":1999872,"nsPerOp":139.589,"checksum":0}
{"lang":"java","bits":256,"op":"MUL_MOD","ops":499712,"nsPerOp":387.031,"checksum":0}
{"lang":"java","bits":256,"op":"MODPOW","ops":7936,"nsPerOp":17764.884,"checksum":0}
{"lang":"java","bits":1024,"op":"ADD_MOD","ops":999424,"nsPerOp":284.672,"checksum":0}
{"lang":"java","bits":1024,"op":"MUL_MOD","ops":119808,"nsPerOp":3094.540,"checksum":0}
{"lang":"java","bits":1024,"op":"MODPOW","ops":1280,"nsPerOp":264577.852,"checksum":0}
{"lang":"java","bits":4096,"op":"ADD_MOD","ops":199680,"nsPerOp":900.735,"checksum":0}
{"lang":"java","bits":4096,"op":"MUL_MOD","ops":19456,"nsPerOp":32062.554,"checksum":0}
{"lang":"java","bits":4096,"op":"MODPOW","ops":256,"nsPerOp":3422756.113,"checksum":0}.NET 10:results_csharp.jsonl
jsonl
{"lang":"csharp","bits":256,"op":"ADD_MOD","ops":1999872,"nsPerOp":146.261,"checksum":0}
{"lang":"csharp","bits":256,"op":"MUL_MOD","ops":499712,"nsPerOp":560.246,"checksum":0}
{"lang":"csharp","bits":256,"op":"MODPOW","ops":7936,"nsPerOp":169713.608,"checksum":0}
{"lang":"csharp","bits":1024,"op":"ADD_MOD","ops":999424,"nsPerOp":297.335,"checksum":0}
{"lang":"csharp","bits":1024,"op":"MUL_MOD","ops":119808,"nsPerOp":4792.760,"checksum":0}
{"lang":"csharp","bits":1024,"op":"MODPOW","ops":1280,"nsPerOp":1938407.720,"checksum":0}
{"lang":"csharp","bits":4096,"op":"ADD_MOD","ops":199680,"nsPerOp":1280.760,"checksum":0}
{"lang":"csharp","bits":4096,"op":"MUL_MOD","ops":19456,"nsPerOp":36894.568,"checksum":0}
{"lang":"csharp","bits":4096,"op":"MODPOW","ops":256,"nsPerOp":20617970.004,"checksum":0}实验二:加入 Java 8 ------看"现状主流"处于什么位置
这一组的关键点是:同一份 Java 源码用 Java 8 编译,分别在 Java 8 与 Java 21 上运行,尽量避免"编译器产物差异"。
4.1 运行方式
bash
# 编译(Java 8)
/path/to/jdk8/bin/javac BigIntBench.java
# 运行(Java 8)
/path/to/jdk8/bin/java -Xms1g -Xmx1g -XX:+UseG1GC -XX:+AlwaysPreTouch BigIntBench --json
# 运行(Java 21)
java -Xms1g -Xmx1g -XX:+UseG1GC -XX:+AlwaysPreTouch BigIntBench --json4.2 实验二原始输出(JSONL)
Java 8:results_java8.jsonl
jsonl
{"lang":"java","bits":256,"op":"ADD_MOD","ops":1999872,"nsPerOp":207.335,"checksum":0}
{"lang":"java","bits":256,"op":"MUL_MOD","ops":499712,"nsPerOp":468.248,"checksum":0}
{"lang":"java","bits":256,"op":"MODPOW","ops":7936,"nsPerOp":17697.113,"checksum":0}
{"lang":"java","bits":1024,"op":"ADD_MOD","ops":999424,"nsPerOp":390.906,"checksum":0}
{"lang":"java","bits":1024,"op":"MUL_MOD","ops":119808,"nsPerOp":3089.474,"checksum":0}
{"lang":"java","bits":1024,"op":"MODPOW","ops":1280,"nsPerOp":277395.652,"checksum":0}
{"lang":"java","bits":4096,"op":"ADD_MOD","ops":199680,"nsPerOp":990.708,"checksum":0}
{"lang":"java","bits":4096,"op":"MUL_MOD","ops":19456,"nsPerOp":30692.214,"checksum":0}
{"lang":"java","bits":4096,"op":"MODPOW","ops":256,"nsPerOp":3468269.539,"checksum":0}可视化与总结
从一个 .NET 程序员的视角来看,这次的测试结果可以说既在情理之中,又有些出乎意料。
- ADD_MOD (加法+取模) : 在这个项目上,.NET 和 Java 21 几乎打了个平手,差距微乎其微。可以说,在基础的加法运算上,.NET 表现得相当不错。
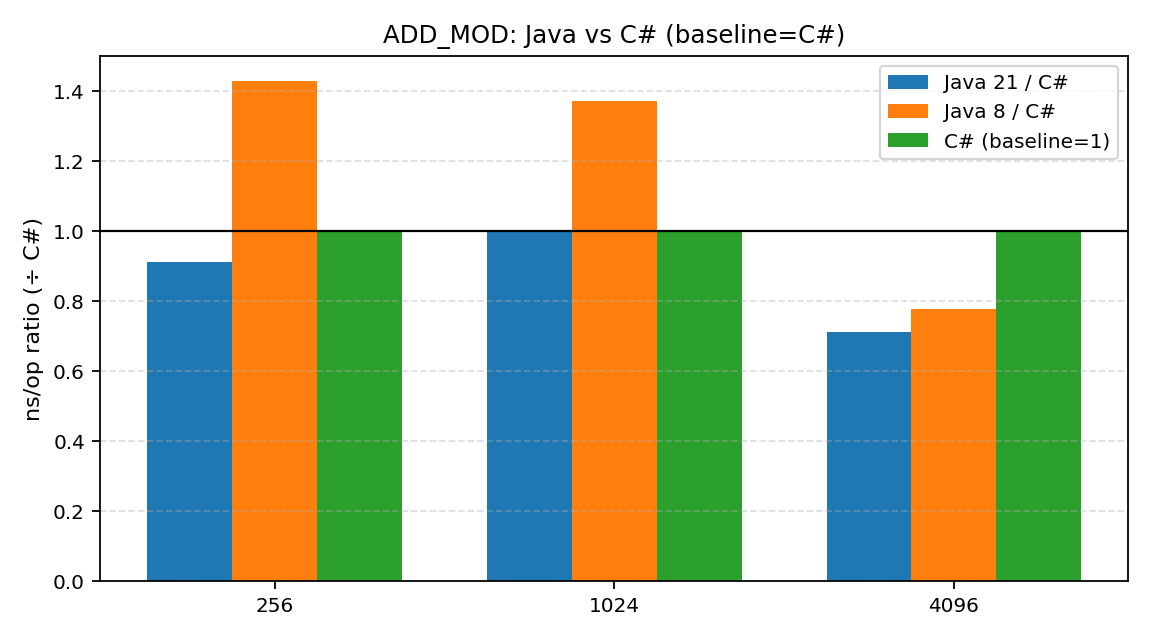
- MUL_MOD (乘法+取模) : 从这里开始,差距出现了。.NET 明显慢于 Java,性能鸿沟开始变得"肉眼可见"。
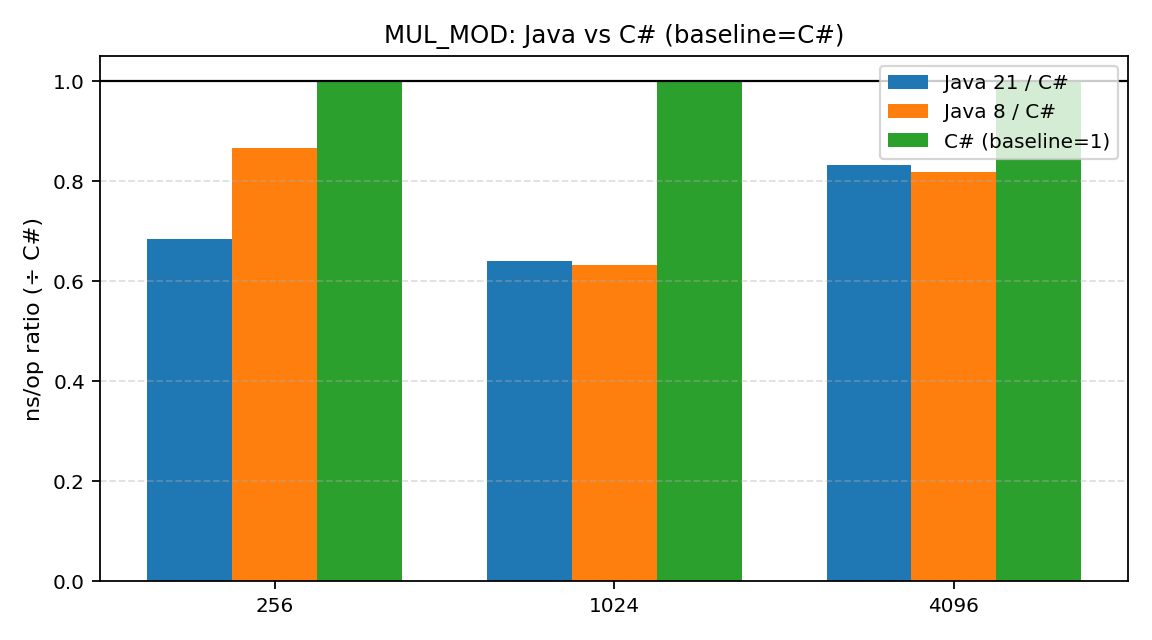
- MODPOW (模幂) : 这是差距最大的地方。.NET 在这项测试中被 Java 21 拉开了 6到9倍 的差距。对于从事密码学或需要大量大数运算的开发者来说,这是一个非常刺眼的信号。
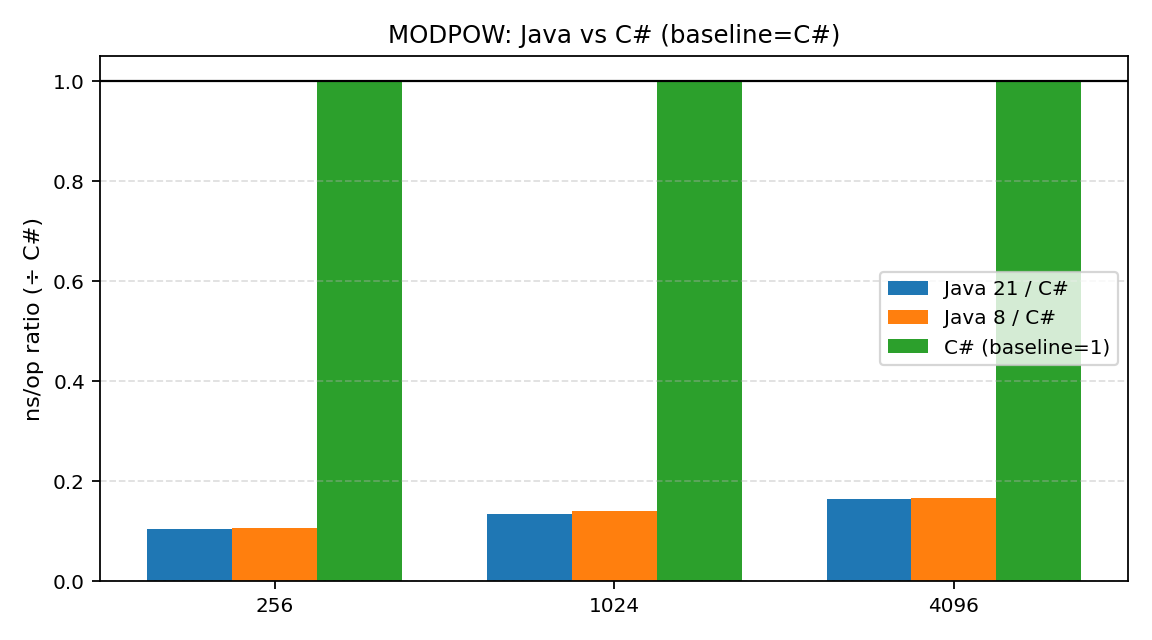
- Java 8 vs Java 21 : 毫无疑问,Java 21 在绝大多数情况下都比老迈的 Java 8 要快。不过有趣的是,在
MUL_MOD的 1024 和 4096 位测试中,Java 8 居然出现了"反超"的现象。这可能是由于 JIT 策略、算法选择的阈值差异,或是单纯的测量误差。虽然这不影响"Java 21更快"的总体结论,但也提醒我们性能测试的复杂性。
总而言之,这次对决让我们清楚地看到,在复杂的大数运算上,.NET 的 BigInteger 确实还有很长的路要走。
One More Thing:当"外援"登场
在寻找 .NET 大数性能优化方案的过程中,我们自然能想到了业界标杆 GMP ------它是 GNU Multi-Precision Arithmetic Library,很多数学软件/密码学实现都会用它做高性能大整数运算。
我碰巧也为它做了一个 .NET 封装:Sdcb.Arithmetic。
但必须提前声明:让 GMP 作为"外援"加入这场对比,是"不公平"的。原因很简单:
- 语言优势:GMP 是原生 C/汇编,而 .NET 和 Java 是在虚拟机上运行的托管语言。
- 内存策略 :GMP 鼓励使用 in-place API ,可以直接在原地修改数值,大大减少了内存分配和 GC 压力。而 .NET 和 Java 的
BigInteger则是不可变对象。
所以,这部分的结果更像是一个"彩蛋",展示的是:如果你愿意引入原生依赖,并改变编码风格,.NET 的大数性能可以达到怎样的高度。
7.1 客串实验完整源代码(.NET BigInteger + GmpInteger 同场)
下面代码会同时输出两套结果:
csharp_bigint与csharp_gmp_inplace(仍是 JSONL)。
Program.cs(客串版,完整)
csharp
using System;
using System.Collections.Generic;
using System.Diagnostics;
using System.Globalization;
using System.Linq;
using System.Numerics;
using Sdcb.Arithmetic.Gmp;
sealed class SplitMix64
{
private ulong _x;
public SplitMix64(ulong seed) => _x = seed;
public ulong NextUInt64()
{
ulong z = (_x += 0x9E3779B97F4A7C15UL);
z = (z ^ (z >> 30)) * 0xBF58476D1CE4E5B9UL;
z = (z ^ (z >> 27)) * 0x94D049BB133111EBUL;
return z ^ (z >> 31);
}
public void NextBytes(byte[] dst)
{
int i = 0;
while (i < dst.Length)
{
ulong v = NextUInt64();
for (int k = 0; k < 8 && i < dst.Length; k++)
dst[i++] = (byte)(v >> (56 - 8 * k));
}
}
}
enum Op { ADD_MOD, MUL_MOD, MODPOW }
record Result(string Impl, int Bits, Op Op, long Ops, double NsPerOp, long Checksum)
{
public string ToJson() => string.Create(CultureInfo.InvariantCulture,
$"{{\"lang\":\"{Impl}\",\"bits\":{Bits},\"op\":\"{Op}\",\"ops\":{Ops},\"nsPerOp\":{NsPerOp:F3},\"checksum\":{Checksum}}}");
}
static class BenchUtil
{
public static void MaskToBitSize(byte[] buf, int bitSize)
{
int topBit = (bitSize - 1) % 8;
int keepBits = topBit + 1;
int firstMask = keepBits == 8 ? 0xFF : ((1 << keepBits) - 1);
buf[0] &= (byte)firstMask;
buf[0] |= (byte)(1 << topBit);
}
public static string ToHex(byte[] bytes) => Convert.ToHexString(bytes);
}
static class BigIntegerBench
{
public static BigInteger[] Gen(int bitSize, int count, ulong seed)
{
var rng = new SplitMix64(seed);
int byteLen = (bitSize + 7) / 8;
var arr = new BigInteger[count];
var buf = new byte[byteLen];
for (int i = 0; i < count; i++)
{
rng.NextBytes(buf);
BenchUtil.MaskToBitSize(buf, bitSize);
arr[i] = new BigInteger(buf, isUnsigned: true, isBigEndian: true);
}
return arr;
}
public static BigInteger GenModulus(int bitSize, ulong seed)
{
var rng = new SplitMix64(seed);
int byteLen = (bitSize + 7) / 8;
var buf = new byte[byteLen];
rng.NextBytes(buf);
BenchUtil.MaskToBitSize(buf, bitSize);
buf[^1] |= 1;
return new BigInteger(buf, isUnsigned: true, isBigEndian: true);
}
public static long RunOnce(Op op, BigInteger[] a, BigInteger[] b, BigInteger[] e, BigInteger mod, int outer)
{
BigInteger acc = BigInteger.Zero;
int n = a.Length;
switch (op)
{
case Op.ADD_MOD:
for (int o = 0; o < outer; o++)
for (int i = 0; i < n; i++)
acc ^= (a[i] + b[i]) % mod;
break;
case Op.MUL_MOD:
for (int o = 0; o < outer; o++)
for (int i = 0; i < n; i++)
acc ^= (a[i] * b[i]) % mod;
break;
case Op.MODPOW:
for (int o = 0; o < outer; o++)
for (int i = 0; i < n; i++)
acc ^= BigInteger.ModPow(a[i], e[i], mod);
break;
}
return (long)(acc & long.MaxValue);
}
}
static class GmpIntegerBench
{
public static GmpInteger[] Gen(int bitSize, int count, ulong seed)
{
var rng = new SplitMix64(seed);
int byteLen = (bitSize + 7) / 8;
var arr = new GmpInteger[count];
var buf = new byte[byteLen];
for (int i = 0; i < count; i++)
{
rng.NextBytes(buf);
BenchUtil.MaskToBitSize(buf, bitSize);
arr[i] = GmpInteger.Parse(BenchUtil.ToHex(buf), 16);
}
return arr;
}
public static GmpInteger GenModulus(int bitSize, ulong seed)
{
var rng = new SplitMix64(seed);
int byteLen = (bitSize + 7) / 8;
var buf = new byte[byteLen];
rng.NextBytes(buf);
BenchUtil.MaskToBitSize(buf, bitSize);
buf[^1] |= 1;
return GmpInteger.Parse(BenchUtil.ToHex(buf), 16);
}
public static long RunOnce(Op op, GmpInteger[] a, GmpInteger[] b, GmpInteger[] e, GmpInteger mod, int outer)
{
using var acc = GmpInteger.From(0);
using var tmp = GmpInteger.From(0);
int n = a.Length;
switch (op)
{
case Op.ADD_MOD:
for (int o = 0; o < outer; o++)
for (int i = 0; i < n; i++)
{
GmpInteger.AddInplace(tmp, a[i], b[i]);
GmpInteger.ModInplace(tmp, tmp, mod);
GmpInteger.BitwiseXorInplace(acc, acc, tmp);
}
break;
case Op.MUL_MOD:
for (int o = 0; o < outer; o++)
for (int i = 0; i < n; i++)
{
GmpInteger.MultiplyInplace(tmp, a[i], b[i]);
GmpInteger.ModInplace(tmp, tmp, mod);
GmpInteger.BitwiseXorInplace(acc, acc, tmp);
}
break;
case Op.MODPOW:
for (int o = 0; o < outer; o++)
for (int i = 0; i < n; i++)
{
GmpInteger.PowerModInplace(tmp, a[i], e[i], mod);
GmpInteger.BitwiseXorInplace(acc, acc, tmp);
}
break;
}
return acc.GetHashCode();
}
public static void DisposeAll(GmpInteger[] xs)
{
foreach (var x in xs) x.Dispose();
}
}
static class Runner
{
static Result BenchBigInteger(int bits, Op op, BigInteger[] a, BigInteger[] b, BigInteger[] e, BigInteger mod, long targetOps, int warmups, int measures)
{
int n = a.Length;
int outer = (int)Math.Max(1, targetOps / n);
long actualOps = (long)n * outer;
long ck = 0;
for (int i = 0; i < warmups; i++) ck ^= BigIntegerBench.RunOnce(op, a, b, e, mod, outer);
long[] timesNs = new long[measures];
for (int i = 0; i < measures; i++)
{
var sw = Stopwatch.StartNew();
long c = BigIntegerBench.RunOnce(op, a, b, e, mod, outer);
sw.Stop();
ck ^= c;
timesNs[i] = (long)(sw.ElapsedTicks * (1_000_000_000.0 / Stopwatch.Frequency));
}
Array.Sort(timesNs);
long median = timesNs[timesNs.Length / 2];
return new Result("csharp_bigint", bits, op, actualOps, (double)median / actualOps, ck);
}
static Result BenchGmpInteger(int bits, Op op, GmpInteger[] a, GmpInteger[] b, GmpInteger[] e, GmpInteger mod, long targetOps, int warmups, int measures)
{
int n = a.Length;
int outer = (int)Math.Max(1, targetOps / n);
long actualOps = (long)n * outer;
long ck = 0;
for (int i = 0; i < warmups; i++) ck ^= GmpIntegerBench.RunOnce(op, a, b, e, mod, outer);
long[] timesNs = new long[measures];
for (int i = 0; i < measures; i++)
{
var sw = Stopwatch.StartNew();
long c = GmpIntegerBench.RunOnce(op, a, b, e, mod, outer);
sw.Stop();
ck ^= c;
timesNs[i] = (long)(sw.ElapsedTicks * (1_000_000_000.0 / Stopwatch.Frequency));
}
Array.Sort(timesNs);
long median = timesNs[timesNs.Length / 2];
return new Result("csharp_gmp_inplace", bits, op, actualOps, (double)median / actualOps, ck);
}
public static int Run(string[] args)
{
bool json = args.Any(a => a == "--json");
int warmups = 5;
int measures = 11;
int[] bitSizes = [256, 1024, 4096];
var results = new List<Result>();
foreach (int bits in bitSizes)
{
long addOps = bits switch { 256 => 2_000_000L, 1024 => 1_000_000L, _ => 200_000L };
long mulOps = bits switch { 256 => 500_000L, 1024 => 120_000L, _ => 20_000L };
long powOps = bits switch { 256 => 8_000L, 1024 => 1_500L, _ => 250L };
// BigInteger data
var modB = BigIntegerBench.GenModulus(bits, 0xA1B2C3D4E5F60708UL ^ (uint)bits);
var aB = BigIntegerBench.Gen(bits, 1024, 0x1111222233334444UL ^ (uint)bits);
var bB = BigIntegerBench.Gen(bits, 1024, 0x9999AAAABBBBCCCCUL ^ (uint)bits);
var apB = BigIntegerBench.Gen(bits, 256, 0x13579BDF2468ACE0UL ^ (uint)bits);
var epB = BigIntegerBench.Gen(Math.Min(bits, 512), 256, 0x0FEDCBA987654321UL ^ (uint)bits);
// GmpInteger data (same seeds/bit sizes)
using var modG = GmpIntegerBench.GenModulus(bits, 0xA1B2C3D4E5F60708UL ^ (uint)bits);
var aG = GmpIntegerBench.Gen(bits, 1024, 0x1111222233334444UL ^ (uint)bits);
var bG = GmpIntegerBench.Gen(bits, 1024, 0x9999AAAABBBBCCCCUL ^ (uint)bits);
var apG = GmpIntegerBench.Gen(bits, 256, 0x13579BDF2468ACE0UL ^ (uint)bits);
var epG = GmpIntegerBench.Gen(Math.Min(bits, 512), 256, 0x0FEDCBA987654321UL ^ (uint)bits);
try
{
results.Add(BenchBigInteger(bits, Op.ADD_MOD, aB, bB, null!, modB, addOps, warmups, measures));
results.Add(BenchBigInteger(bits, Op.MUL_MOD, aB, bB, null!, modB, mulOps, warmups, measures));
results.Add(BenchBigInteger(bits, Op.MODPOW, apB, null!, epB, modB, powOps, warmups, measures));
results.Add(BenchGmpInteger(bits, Op.ADD_MOD, aG, bG, null!, modG, addOps, warmups, measures));
results.Add(BenchGmpInteger(bits, Op.MUL_MOD, aG, bG, null!, modG, mulOps, warmups, measures));
results.Add(BenchGmpInteger(bits, Op.MODPOW, apG, null!, epG, modG, powOps, warmups, measures));
}
finally
{
GmpIntegerBench.DisposeAll(aG);
GmpIntegerBench.DisposeAll(bG);
GmpIntegerBench.DisposeAll(apG);
GmpIntegerBench.DisposeAll(epG);
}
}
if (json)
{
foreach (var r in results) Console.WriteLine(r.ToJson());
}
return 0;
}
}
public static class Program
{
public static int Main(string[] args) => Runner.Run(args);
}gmpbench.csproj(客串版项目文件)
xml
<Project Sdk="Microsoft.NET.Sdk">
<PropertyGroup>
<OutputType>Exe</OutputType>
<TargetFramework>net10.0</TargetFramework>
<Nullable>enable</Nullable>
<ImplicitUsings>enable</ImplicitUsings>
</PropertyGroup>
<ItemGroup>
<PackageReference Include="Sdcb.Arithmetic.Gmp" Version="*" />
<PackageReference Include="Sdcb.Arithmetic.Gmp.runtime.linux-x64" Version="*" />
</ItemGroup>
</Project>7.2 客串实验原始输出(JSONL)
jsonl
{"lang":"csharp_bigint","bits":256,"op":"ADD_MOD","ops":1999872,"nsPerOp":146.261,"checksum":0}
{"lang":"csharp_bigint","bits":256,"op":"MUL_MOD","ops":499712,"nsPerOp":560.246,"checksum":0}
{"lang":"csharp_bigint","bits":256,"op":"MODPOW","ops":7936,"nsPerOp":169713.608,"checksum":0}
{"lang":"csharp_gmp_inplace","bits":256,"op":"ADD_MOD","ops":1999872,"nsPerOp":76.644,"checksum":0}
{"lang":"csharp_gmp_inplace","bits":256,"op":"MUL_MOD","ops":499712,"nsPerOp":114.690,"checksum":0}
{"lang":"csharp_gmp_inplace","bits":256,"op":"MODPOW","ops":7936,"nsPerOp":13931.914,"checksum":0}
{"lang":"csharp_bigint","bits":1024,"op":"ADD_MOD","ops":999424,"nsPerOp":297.335,"checksum":0}
{"lang":"csharp_bigint","bits":1024,"op":"MUL_MOD","ops":119808,"nsPerOp":4792.760,"checksum":0}
{"lang":"csharp_bigint","bits":1024,"op":"MODPOW","ops":1280,"nsPerOp":1938407.720,"checksum":0}
{"lang":"csharp_gmp_inplace","bits":1024,"op":"ADD_MOD","ops":999424,"nsPerOp":97.260,"checksum":0}
{"lang":"csharp_gmp_inplace","bits":1024,"op":"MUL_MOD","ops":119808,"nsPerOp":562.235,"checksum":0}
{"lang":"csharp_gmp_inplace","bits":1024,"op":"MODPOW","ops":1280,"nsPerOp":218715.147,"checksum":0}
{"lang":"csharp_bigint","bits":4096,"op":"ADD_MOD","ops":199680,"nsPerOp":1280.760,"checksum":0}
{"lang":"csharp_bigint","bits":4096,"op":"MUL_MOD","ops":19456,"nsPerOp":36894.568,"checksum":0}
{"lang":"csharp_bigint","bits":4096,"op":"MODPOW","ops":256,"nsPerOp":20617970.004,"checksum":0}
{"lang":"csharp_gmp_inplace","bits":4096,"op":"ADD_MOD","ops":199680,"nsPerOp":179.720,"checksum":0}
{"lang":"csharp_gmp_inplace","bits":4096,"op":"MUL_MOD","ops":19456,"nsPerOp":5431.441,"checksum":0}
{"lang":"csharp_gmp_inplace","bits":4096,"op":"MODPOW","ops":256,"nsPerOp":2662198.492,"checksum":0}7.3 客串可视化(以GMP为基准)
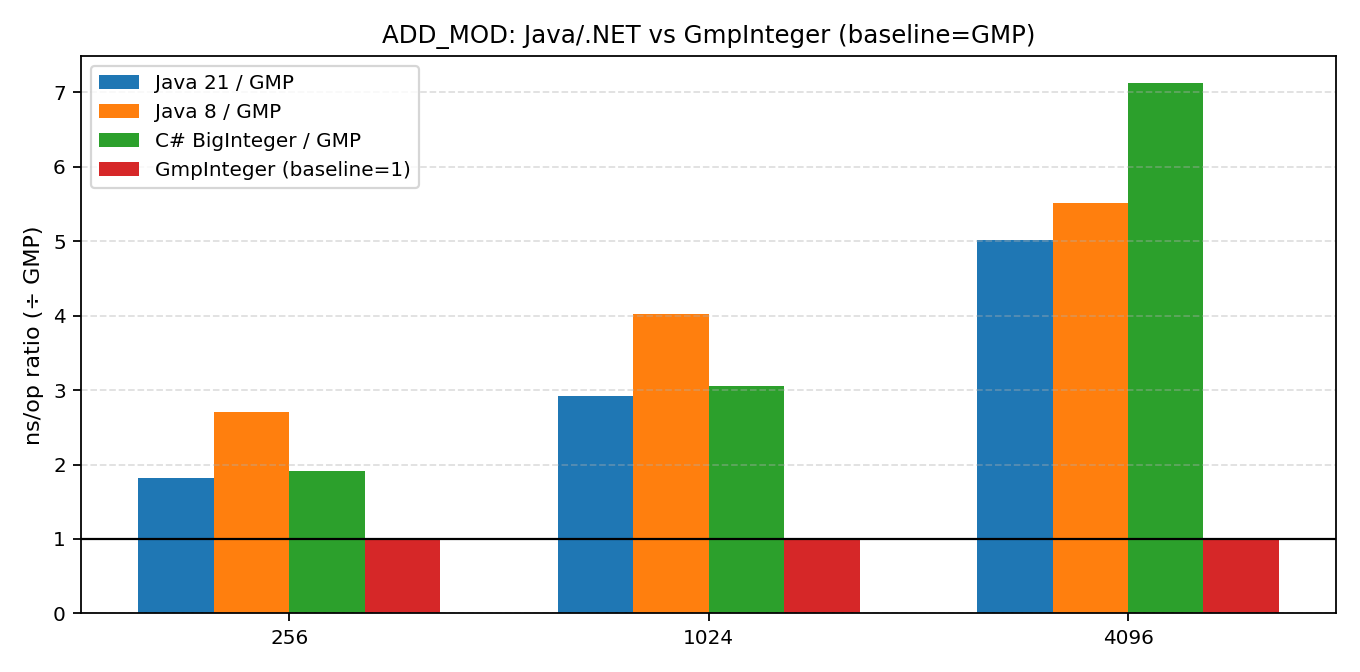
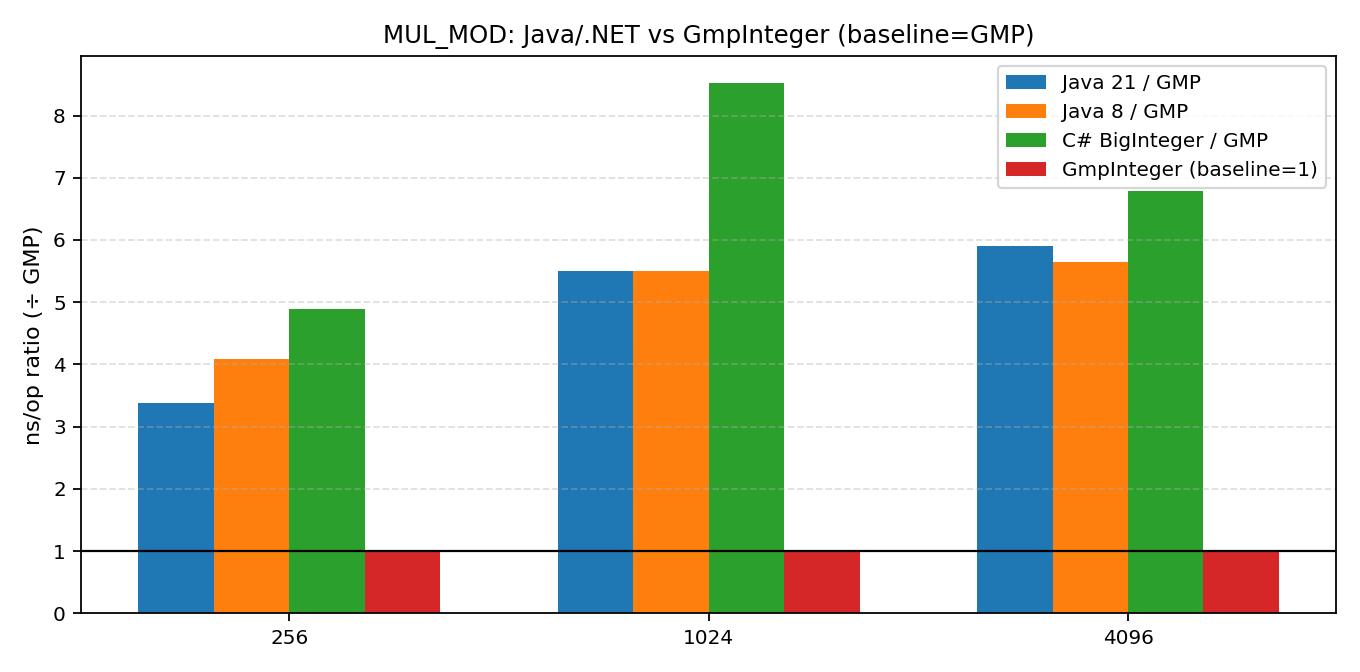
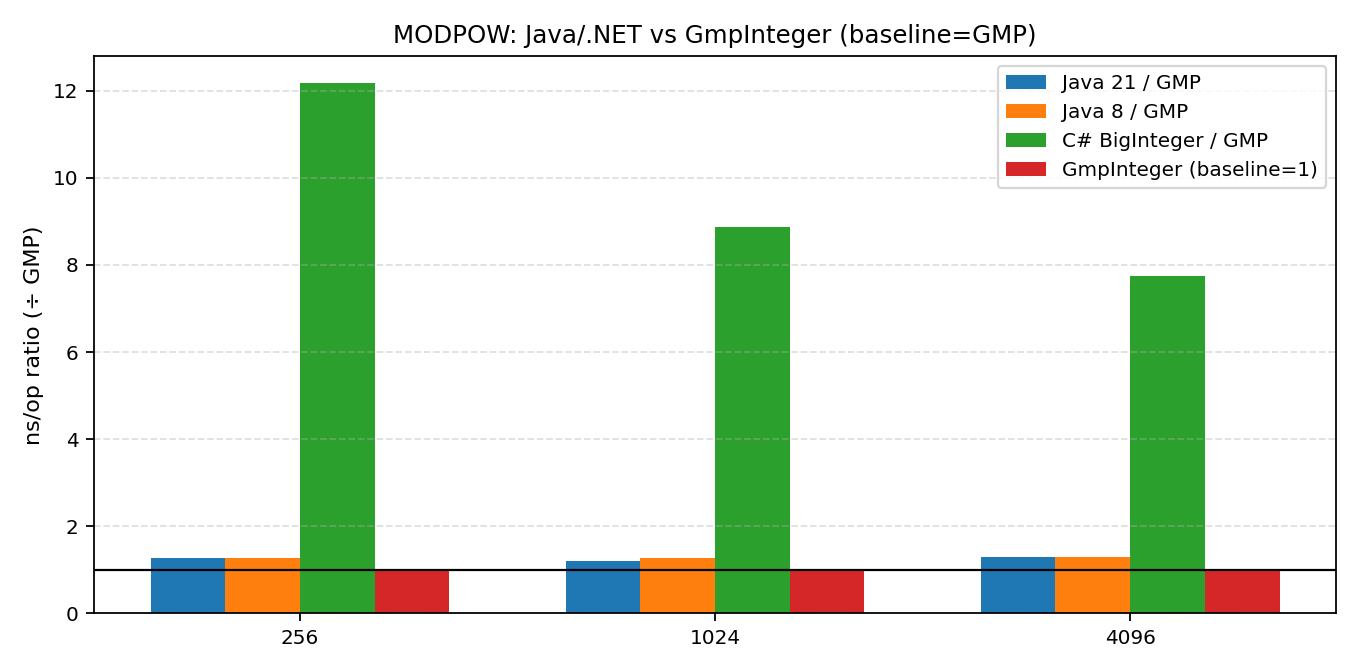
总结与展望
从这次"硬碰硬"的对决中,我们可以清晰地看到:在基础加法上,.NET BigInteger 与 Java 不分伯仲;但在乘法,尤其是模幂运算(对密码学等场景极其重要)上,.NET 目前确实存在明显的短板,大幅落后于 Java。
承认不足是改进的开始。对于绝大多数业务场景,内置的 BigInteger 依然够用且方便。但如果你的应用处于性能敏感区(如加密算法、科学计算),那么也许是时候考虑一些"重武器"了。
这也正是我开发并维护 Sdcb.Arithmetic 的初衷。它通过封装 GMP 等高性能原生库,为 .NET 带来了**原地修改(in-place)**以及高达数倍的性能提升(如文中实验所示)。如果你对性能有极致追求,或者想看看 .NET 在大数计算上的极限,欢迎去 GitHub 点个 Star ⭐,试一试这个库。
感谢阅读!如果你觉得这两个语言的对比分析有意思,或者对 .NET 高性能编程感兴趣,欢迎在评论区留言交流,也欢迎加入我的 .NET骚操作 QQ群:495782587,我们一起探索更多技术硬核玩法。