堆的完全二叉树实现

堆的概念

1. 堆的定义

堆 （Heap）是一种特殊的完全二叉树，它满足以下两个核心性质：

（1）结构性质

• 堆必须是一棵 完全二叉树 （Complete Binary Tree）
  → 除最后一层外，其他层全部填满；最后一层结点靠左连续排列。

（2）堆序性质（Heap Order Property）

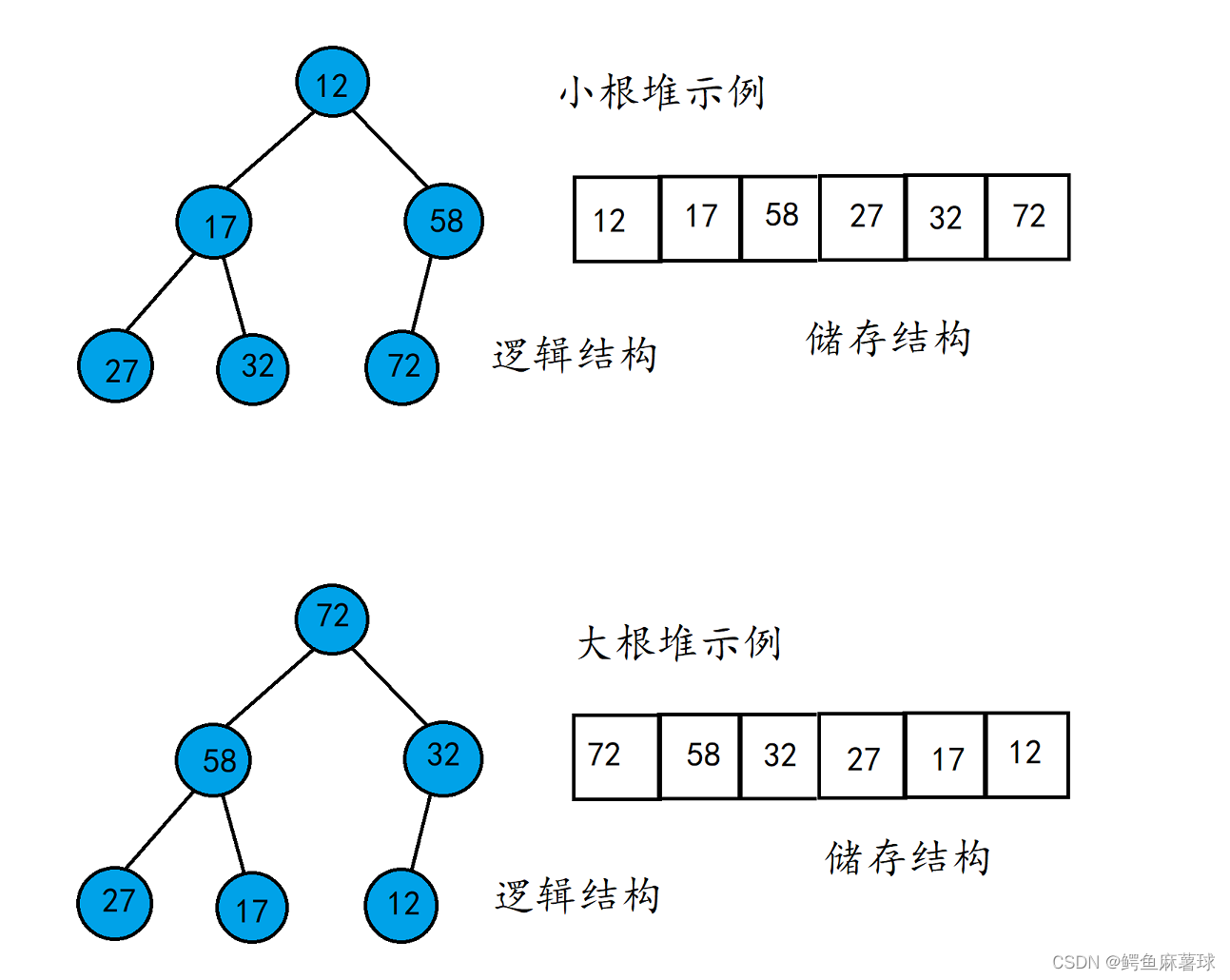
• 最大堆 （大根堆）：任意结点的值 ≥ 其子结点的值；
  → 根结点是最大值。
• 最小堆 （小根堆）：任意结点的值 ≤ 其子结点的值；
  → 根结点是最小值。

堆中不要求左右子树有序 ，只要求父与子之间满足大小关系。
堆本身的结构决定了他不能在堆中间随意插入数据，也不能从中间删除数据，否则会破坏原有的亲子关系

---

实现堆前，我们需要学习两个调整堆的算法

堆的向上调整算法（Heapify Up / Percolate Up）

一、算法目的

当向堆中插入一个新元素 （通常放在数组末尾）后，该元素可能破坏堆的有序性 。
向上调整算法 的作用是：从该新结点开始，沿着父路径向上比较并交换，直到恢复堆序性质。

前提：插入前原结构是一个合法的堆。

---

二、适用场景

• 堆的插入操作（Push）；
• 修改堆中某个元素使其变小 （最小堆）或变大 （最大堆）后恢复堆序。（若该结点的值被"恶化"（例如在小堆中变成了大于其任意子节点的值），需要的是向下调整）
• 建立堆

---

三、算法思想（以最小堆为例）

1. 将新元素插入到数组末尾（即完全二叉树的最后一个位置）；
2. 从该位置开始，与其父结点 比较：
   • 如果 当前结点 < 父结点，则交换；
3. 将当前位置移动到父结点；
4. 重复上述过程，直到：
   • 当前结点 ≥ 父结点（满足堆序），或
   • 到达根结点（i == 0）。

对最大堆 ，只需将比较条件改为：当前结点 > 父结点。

---

四、代码实现

小堆版

void AdjustUP(HPDataType* a, int child)//向上调整法，child需要调整的数据一般为最后一个叶子，如果为某存在子树的子节点时，要求节点的子树必须为合法堆。该算法只能向堆尾插入数据，因为堆本身不支持随意插入数据，否则会改变亲树和子树的关系。但是它可以用于修改数据，修改时要注意其堆本身的特性和大小，例如在小堆的中间节点中修改出一个大于其所有字节点的数据时，算法只会向上调整，不会向下调整，就会破坏堆的合法性，此时应该调用向下调整法。
{
	int parent = (child - 1) / 2;
	while (child>0)
	{
		if (a[parent] > a[child])
		{
			Swap(&a[parent], &a[child]);
		}
		child = parent;
		parent = (child - 1) / 2;
	}
}

堆的向下调整算法（Heapify Down）

一、算法目的

将一个几乎满足堆性质 的完全二叉树（以数组形式存储）中某个可能破坏堆序的结点 ，通过与其子结点的比较和交换，向下调整，使其子树重新满足堆的性质。

前提条件 ：该结点的左子树和右子树已经是堆。

---

二、适用场景

• 删除堆顶元素后重建堆；（这里是用向下排序是因为删除栈顶元素时会将叶子替换到栈顶，会破坏堆结构，但是他的子树依旧还是堆结构，向下调整可以向下见检查，恢复堆的合法性）
• 建堆过程中从下往上调整；
• 修改堆中某个元素后恢复堆序。
• 建立堆

---

三、算法思想（以小根堆为例）

1. 从指定结点 i 开始；
2. 找出其左右孩子中的较小者；
3. 如果当前结点 > 较小孩子，则交换；（目的是如果发生交换，可以是使得交换上来的节点小于所有子节点，也就是小于该节点原来的兄弟节点）
4. 将当前位置移动到被交换的孩子位置；
5. 重复上述过程，直到：
   • 当前结点 ≤ 所有孩子（满足堆序），或
   • 到达叶子结点（无孩子）。

---

四、代码实现

小根堆版本：

void AdjustDown(HPDataType* a,int n, int parent)//parent 是目标调整节点的当前位置（通常是 0）；那个"从末尾换上来的元素"现在就在 parent 位置（如 a[0]）；我们要把它"沉"到合适的位置。
//参数n实际是你希望调整的元素数量，若你希望全调整则传入数组大小size，即对堆中前n个元素进行向下调整
//向下排序法用于堆排序，要求除去根元素外所有元素是合法堆
{
	int child= parent * 2 + 1;

	while (child < n)
	{
		if (child + 1 < n && a[child + 1] < a[child])//找出最小的子节点,同时保证右孩子没有越界
		{
			child++;
		}

		if (a[parent] > a[child])//判断时是否大于最小节点，因为取其他节点，即使父节点小也不能说明堆合法，小于最小节点一定小于其他节点，而且关键是要保证替换上来的该节点小于他的子节点（也就是还没替换前的兄弟节点）

		{
			Swap(&a[parent], &a[child]);
			parent = child;//在替换前，除了根，其他部位一定满足堆结构（因为入堆时生成的堆一定是合法的，交换后只有根一个元素可能非法），所以只要一直检查该元素的子元素是否满足小堆排序就够了，一旦满足就可以停止检查。
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}

完整实现代码

heap.h

#pragma once

#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>

typedef int HPDataType;
typedef struct Heap
{
	HPDataType* _a;
	int _size;
	int _capacity;
}Heap;

void HeapInit(Heap* hp);
// 堆的销毁
void HeapDestory(Heap* hp);
// 堆的插入
void HeapPush(Heap* hp, HPDataType x);
// 堆的删除
void HeapPop(Heap* hp);
// 取堆顶的数据
HPDataType HeapTop(Heap* hp);
// 堆的数据个数
int HeapSize(Heap* hp);
// 堆的判空
bool HeapEmpty(Heap* hp);
//调整堆
void AdjustUP(HPDataType* a, int child);

heap.c

void HeapInit(Heap* hp)
{
	hp->_a = NULL;
	hp->_size = 0;
	hp->_capacity = 0;

}

void Swap(HPDataType* a1, HPDataType* a2)
{
	HPDataType temp;
	temp = *a1;
	*a1 = *a2;
	*a2 = temp;
}
// 堆的销毁
void AdjustUP(HPDataType* a, int child)//向上调整法，child是插入的最后一个数据
//向上调整法用于建立大堆/小堆，要求调整前除了最后一个叶子整体为合法堆
{
	int parent = (child - 1) / 2;
	while (child>0)
	{
		if (a[parent] > a[child])
		{
			Swap(&a[parent], &a[child]);
		}
		child = parent;
		parent = (child - 1) / 2;
	}
}
void AdjustDown(HPDataType* a,int n, int parent)//parent 是目标调整节点的当前位置（通常是 0）；那个"从末尾换上来的元素"现在就在 parent 位置（如 a[0]）；我们要把它"沉"到合适的位置。
//参数n实际是你希望调整的元素数量，若你希望全调整则传入数组大小size，即对堆中前n个元素进行向下调整
//向下排序法用于堆排序，要求除去根元素外所有元素是合法堆
{
	int child= parent * 2 + 1;

	while (child < n)
	{
		if (child + 1 < n && a[child + 1] < a[child])//找出最小的子节点,同时保证右孩子没有越界
		{
			child++;
		}

		if (a[parent] > a[child])//判断时是否大于最小节点，因为取其他节点，即使父节点小也不能说明堆合法，小于最小节点一定小于其他节点，而且关键是要保证替换上来的该节点小于他的子节点（也就是还没替换前的兄弟节点）

		{
			Swap(&a[parent], &a[child]);
			parent = child;//在替换前，除了根，其他部位一定满足堆结构（因为入堆时生成的堆一定是合法的，交换后只有根一个元素可能非法），所以只要一直检查该元素的子元素是否满足小堆排序就够了，一旦满足就可以停止检查。
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}


	}
}
void HeapDestory(Heap* hp)
{
	free(hp->_a);
	hp->_size = hp->_capacity = 0;
}
// 堆的插入
void HeapPush(Heap* hp, HPDataType x)//向上调整法的前提是插入前的堆是合法堆，但是当我们从空开始插入时，它一定是合法堆，所以这个插入方法一定能得到一个小堆。
{
	if (hp->_size == hp->_capacity)
	{
		int newcapacity = hp->_capacity == 0 ? 4 : hp->_capacity*2;
		HPDataType* temp = (HPDataType*)realloc(hp->_a,newcapacity * sizeof(HPDataType));
		if (temp == NULL)
		{
			perror("realloc error");
			return ;
		}
		hp->_a = temp;
		hp->_capacity = newcapacity;
	}
	hp->_a[hp->_size] = x;
	hp->_size++;
	AdjustUP(hp->_a, hp->_size-1);
}
// 堆的删除
void HeapPop(Heap* hp)//删除堆需要用向下调整法，确保删除完成后堆结构合法
{
	Swap(&hp->_a[0], &hp->_a[hp->_size-1]);//将要删除的根元素换到堆末，堆末要保留的叶子换到根位置，后续用向下调整算法恢复结构
	hp->_size--;
	AdjustDown(hp->_a, hp->_size, 0);
}
// 取堆顶的数据
HPDataType HeapTop(Heap* hp)
{
	return hp->_a[0];
}
// 堆的数据个数
int HeapSize(Heap* hp)
{
	return hp->_size;
}
// 堆的判空
bool HeapEmpty(Heap* hp)
{
	return !hp->_size;
}

操作	位置	是否支持	说明
插入	堆尾（数组末尾）	✅	唯一合法插入点
删除	堆顶	✅	核心操作，获取最值
删除	堆尾	❌	不是标准操作（除非你明确知道它是最值）
删除	中间任意位置	❌	需额外机制，非标准堆功能

虽然可以通过移动下标实现删除堆尾元素，但堆的作用一般是取出最大值或最小值元素，所以堆尾删除并不符合语义

堆排序

使用向上调整或向下调整建立的大堆/小堆并没有完全排序，因为他们只有亲子间符合大小关系，但兄弟间不符合大小关系，想要对堆实现升序或者降序，还需要完成堆排序。

核心思想：

1. 建堆 ：将待排序数组构造成一个大根堆 （升序）或小根堆（降序）；
2. 重复提取堆顶 ：
   • 将堆顶（最大值/最小值）与末尾元素交换；
   • 缩小堆的范围（排除已排好的末尾）；
   • 对新堆顶执行向下调整（Heapify Down），恢复堆性质；
3. 重复步骤 2，直到堆中只剩一个元素。

void HeapSort(int* a, int n)//a为数组，不要求是合法堆,n为元素个数；
{
	//升序建立大堆，降序建立小堆
	for (int i = 0;i < n;i++)
	{
		AdjustUP(a,i);
	}//这是在建堆（该程序中是小堆），从零开始依次向上调整就相当于从零开插入数据，保证在i以内都是合法堆

	/*
	* for (int i = (n-2)/2;i >= 0;i--)//（n-1-1）/2是末叶子的亲树，叶子无子树，不要调整，直接从最远的亲树开始。n-1为最后一个叶子的下标
	{
		AdjustDown(a,n,i);//参数n是有效容量，内部逻辑会自己调整
	}//向下调整法建堆，效率由于向上调整法逐步建堆
	*/

	int end = n - 1;
	while (end>0)
	{
		//堆排序核心，类似于删除堆中首元素的操作，以降序为例，将根元素换到末尾后，再次进行排序，每次调整都将最小的根元素排至当前堆的末尾；
		Swap(&a[0], &a[end]);
		AdjustDown(a, end, 0);//这里的end最初传入n-1而非n是为了避免将本来已经排序好的最后一个叶子重新排进原始堆里
		end--;
	}
}