陷波滤波器 | 原理、特性、设计及应用

斐夷所非2026-01-17 17:26

注：本文为 "陷波滤波器" 相关合辑。

图片清晰度受引文原图所限。

略作重排，未整理去重。

如有内容异常，请看原文。

陷波滤波器理论与应用

1. 定义

陷波滤波器（Notch Filter），又称点阻滤波器，是一种能够在特定频率点及其附近窄频带内对信号产生大幅衰减，同时对其余频率信号几乎不产生影响的滤波器。其频率响应特性曲线表现为在平坦频段上出现的"凹陷"或"深谷"，凹陷底部对应需要滤除的目标频率。陷波滤波器属于带阻滤波器的一个特例，二者的主要区别在于阻带宽度：陷波滤波器的阻带较窄，而带阻滤波器的阻带通常较宽。

2. 工作原理

陷波滤波器的设计原理是在特定频率点（陷波频率或中心频率）处呈现极高阻抗，从而阻止对应频率的信号通过。对于理想陷波滤波器，其传递函数在陷波频率处的增益为 0，而在其余频率处的增益趋近于 1。在实际应用中，由于物理实现条件的限制，无法完全达到理想的零增益点，但可以设计出在特定频率处具有极低增益的滤波器。

2.1 模拟陷波滤波器传递函数

二阶模拟陷波滤波器在拉普拉斯域的通用传递函数形式为：

H ( s ) = K s 2 + 2 ζ z ω 0 s + ω 0 2 s 2 + 2 ζ p ω 0 s + ω 0 2 H(s) = K \frac{s^2 + 2\zeta_z \omega_0 s + \omega_0^2}{s^2 + 2\zeta_p \omega_0 s + \omega_0^2} H(s)=Ks2+2ζpω0s+ω02s2+2ζzω0s+ω02

其中参数说明如下：

  • K K K 为增益常数
  • ζ z \zeta_z ζz 为零点阻尼比
  • ζ p \zeta_p ζp 为极点阻尼比

当 ζ z = 0 \zeta_z = 0 ζz=0 时，可得到标准二阶陷波滤波器的传递函数：

H ( s ) = s 2 + ω 0 2 s 2 + ω 0 Q s + ω 0 2 H(s) = \frac{s^2 + \omega_0^2}{s^2 + \frac{\omega_0}{Q} s + \omega_0^2} H(s)=s2+Qω0s+ω02s2+ω02

将 s = j ω s = j\omega s=jω 代入上式，可得频率响应表达式：

H ( j ω ) = ( j ω ) 2 + ω 0 2 ( j ω ) 2 + ω 0 Q ( j ω ) + ω 0 2 = ω 0 2 − ω 2 ω 0 2 − ω 2 + j ω 0 ω Q H(j\omega) = \frac{(j\omega)^2 + \omega_0^2}{(j\omega)^2 + \frac{\omega_0}{Q}(j\omega) + \omega_0^2} = \frac{\omega_0^2 - \omega^2}{\omega_0^2 - \omega^2 + j\frac{\omega_0\omega}{Q}} H(jω)=(jω)2+Qω0(jω)+ω02(jω)2+ω02=ω02−ω2+jQω0ωω02−ω2

进一步推导，可得幅频响应表达式：

∣ H ( j ω ) ∣ = ∣ ω 2 − ω 0 2 ∣ ( ω 2 − ω 0 2 ) 2 + ( ω ω 0 Q ) 2 |H(j\omega)| = \frac{|\omega^2 - \omega_0^2|}{\sqrt{(\omega^2 - \omega_0^2)^2 + \left(\frac{\omega\omega_0}{Q}\right)^2}} ∣H(jω)∣=(ω2−ω02)2+(Qωω0)2 ∣ω2−ω02∣

在 ω = ω 0 \omega = \omega_0 ω=ω0 处，理想情况下 ∣ H ( j ω 0 ) ∣ = 0 |H(j\omega_0)| = 0 ∣H(jω0)∣=0。

2.2 数字陷波滤波器传递函数

数字陷波滤波器在 z z z 域的二阶传递函数形式为：

H ( z ) = 1 − 2 cos ⁡ ( ω 0 T ) z − 1 + z − 2 1 − 2 r cos ⁡ ( ω 0 T ) z − 1 + r 2 z − 2 H(z) = \frac{1 - 2\cos(\omega_0 T) z^{-1} + z^{-2}}{1 - 2r\cos(\omega_0 T) z^{-1} + r^2 z^{-2}} H(z)=1−2rcos(ω0T)z−1+r2z−21−2cos(ω0T)z−1+z−2

其中参数说明如下：

  • T T T 为采样周期
  • r r r 为小于 1 的常数，用于控制陷波的带宽
  • ω 0 \omega_0 ω0 为需要消除的数字角频率

将 z = e j ω T z = e^{j\omega T} z=ejωT 代入上式，可得数字陷波滤波器的频率响应：

H ( e j ω T ) = 1 − 2 cos ⁡ ( ω 0 T ) e − j ω T + e − j 2 ω T 1 − 2 r cos ⁡ ( ω 0 T ) e − j ω T + r 2 e − j 2 ω T H(e^{j\omega T}) = \frac{1 - 2\cos(\omega_0 T) e^{-j\omega T} + e^{-j2\omega T}}{1 - 2r\cos(\omega_0 T) e^{-j\omega T} + r^2 e^{-j2\omega T}} H(ejωT)=1−2rcos(ω0T)e−jωT+r2e−j2ωT1−2cos(ω0T)e−jωT+e−j2ωT

利用欧拉公式与三角恒等式化简后，可得到幅频特性表达式：

∣ H ( e j ω T ) ∣ = [ 1 − cos ⁡ ( ω 0 T ) cos ⁡ ( ω T ) ] 2 + [ cos ⁡ ( ω 0 T ) sin ⁡ ( ω T ) ] 2 [ 1 − r cos ⁡ ( ω 0 T ) cos ⁡ ( ω T ) ] 2 + [ r cos ⁡ ( ω 0 T ) sin ⁡ ( ω T ) ] 2 |H(e^{j\omega T})| = \frac{\sqrt{[1 - \cos(\omega_0 T)\cos(\omega T)]^2 + [\cos(\omega_0 T)\sin(\omega T)]^2}}{\sqrt{[1 - r\cos(\omega_0 T)\cos(\omega T)]^2 + [r\cos(\omega_0 T)\sin(\omega T)]^2}} ∣H(ejωT)∣=[1−rcos(ω0T)cos(ωT)]2+[rcos(ω0T)sin(ωT)]2 [1−cos(ω0T)cos(ωT)]2+[cos(ω0T)sin(ωT)]2

2.3 多子级陷波滤波器系统传递函数

对于复杂的陷波滤波器系统，其总体传递函数可通过各子级传递函数的乘积获得：

H total ( s ) = ∏ i = 1 n H i ( s ) H_{\text{total}}(s) = \prod_{i=1}^{n} H_i(s) Htotal(s)=i=1∏nHi(s)

3. 特性参数

理解陷波滤波器的性能需掌握以下特性参数：

  1. 陷波频率

    • 陷波频率分为角频率 ω 0 \omega_0 ω0 与频率 f 0 f_0 f0 两种表述形式，二者的换算关系为 ω 0 = 2 π f 0 \omega_0 = 2\pi f_0 ω0=2πf0，该参数对应滤波器需要抑制的目标频率。

  2. 品质因数

    • 品质因数 Q Q Q 用于衡量陷波滤波器的频率选择特性，定义式为：
      Q = ω 0 Δ ω Q = \frac{\omega_0}{\Delta\omega} Q=Δωω0
      其中 Δ ω \Delta\omega Δω 为陷波的 3dB 带宽。
      • 当 Q Q Q 值较高时，陷波带宽较窄，频率选择特性较好，但会导致瞬态响应时间较长；
      • 当 Q Q Q 值较低时，频率选择特性较差，但瞬态响应时间较短。

  3. 3dB 带宽

    • 3dB 带宽 Δ ω \Delta\omega Δω 可通过求解方程 ∣ H ( j ω ) ∣ 2 = 1 2 |H(j\omega)|^2 = \frac{1}{2} ∣H(jω)∣2=21 得到，表达式为：
      Δ ω = ω 0 Q 1 + 1 4 Q 2 \Delta\omega = \frac{\omega_0}{Q}\sqrt{1 + \frac{1}{4Q^2}} Δω=Qω01+4Q21
      在 Q Q Q 值较高的情况下（ Q > 10 Q > 10 Q>10），可近似为：
      Δ ω ≈ ω 0 Q \Delta\omega \approx \frac{\omega_0}{Q} Δω≈Qω0

  4. 陷波深度

    • 陷波深度指在陷波频率处的信号衰减程度，通常以分贝（dB）为单位表示，计算公式为：
      陷波深度 = − 20 log ⁡ 10 ∣ H ( j ω 0 ) ∣ dB \text{陷波深度} = -20\log_{10}|H(j\omega_0)| \text{ dB} 陷波深度=−20log10∣H(jω0)∣ dB
      理想的陷波深度为无穷大，但在实际设计中，该参数受元件精度与电路实现条件的限制。

4. 类型与实现方式

根据实现方式与应用场景的不同，陷波滤波器可划分为无源 LC 陷波滤波器、有源 RC 陷波滤波器与数字陷波滤波器三类。

4.1 无源 LC 陷波滤波器

无源 LC 陷波滤波器由电感（L）与电容（C）构成，最基础的并联 LC 陷波电路在谐振频率处呈现极低阻抗，从而将对应频率的信号短路至地。

其谐振频率的计算公式为：

f 0 = 1 2 π L C f_0 = \frac{1}{2\pi\sqrt{LC}} f0=2πLC 1

对于并联 LC 陷波网络与负载电阻 R R R 并联的电路，其传递函数为：

H ( s ) = s L s L + 1 s C + R = s 2 L C s 2 L C + 1 + s R C H(s) = \frac{sL}{sL + \frac{1}{sC} + R} = \frac{s^2 LC}{s^2 LC + 1 + sRC} H(s)=sL+sC1+RsL=s2LC+1+sRCs2LC

整理后可得：

H ( s ) = s 2 s 2 + s R C + 1 L C H(s) = \frac{s^2}{s^2 + \frac{s}{RC} + \frac{1}{LC}} H(s)=s2+RCs+LC1s2

与标准二阶陷波滤波器传递函数对比，可得到参数对应关系：

ω 0 = 1 L C Q = R C L = R ω 0 C \begin{aligned} \omega_0 &= \frac{1}{\sqrt{LC}} \\ Q &= R\sqrt{\frac{C}{L}} = R\omega_0 C \end{aligned} ω0Q=LC 1=RLC =Rω0C

4.2 有源 RC 陷波滤波器

有源 RC 陷波滤波器采用运算放大器、电阻与电容实现，无需使用体积较大的电感元件，适用于集成电路的实现场景。

双 T 陷波滤波器是一类常见的有源陷波滤波器拓扑结构，由两个 T 型网络组成，其中一个网络由电阻构成，另一个网络由电容构成。其传递函数为：

H ( s ) = s 2 + ω 0 2 s 2 + α ω 0 s + ω 0 2 H(s) = \frac{s^2 + \omega_0^2}{s^2 + \alpha\omega_0 s + \omega_0^2} H(s)=s2+αω0s+ω02s2+ω02

其中 α \alpha α 是与反馈增益相关的参数，用于控制陷波的 Q Q Q 值。

将其展开为标准形式：

H ( s ) = 1 − s 2 ω 0 2 1 − s 2 ω 0 2 + α s ω 0 H(s) = \frac{1 - \frac{s^2}{\omega_0^2}}{1 - \frac{s^2}{\omega_0^2} + \frac{\alpha s}{\omega_0}} H(s)=1−ω02s2+ω0αs1−ω02s2

令 s = j ω s = j\omega s=jω 进行变量替换，可得频率响应表达式：

H ( j ω ) = 1 − ω 2 ω 0 2 1 − ω 2 ω 0 2 + j α ω ω 0 H(j\omega) = \frac{1 - \frac{\omega^2}{\omega_0^2}}{1 - \frac{\omega^2}{\omega_0^2} + j\frac{\alpha\omega}{\omega_0}} H(jω)=1−ω02ω2+jω0αω1−ω02ω2

其幅频特性表达式为：

∣ H ( j ω ) ∣ = ∣ 1 − ω 2 ω 0 2 ∣ ( 1 − ω 2 ω 0 2 ) 2 + ( α ω ω 0 ) 2 |H(j\omega)| = \frac{|1 - \frac{\omega^2}{\omega_0^2}|}{\sqrt{(1 - \frac{\omega^2}{\omega_0^2})^2 + (\frac{\alpha\omega}{\omega_0})^2}} ∣H(jω)∣=(1−ω02ω2)2+(ω0αω)2 ∣1−ω02ω2∣

4.3 数字陷波滤波器

数字陷波滤波器在数字信号处理系统中实现，其核心为 z z z 域传递函数的离散化运算。直接型 II 结构的差分方程为：

y [ n ] = x [ n ] − 2 cos ⁡ ( ω 0 ) x [ n − 1 ] + x [ n − 2 ] + 2 r cos ⁡ ( ω 0 ) y [ n − 1 ] − r 2 y [ n − 2 ] y[n] = x[n] - 2\cos(\omega_0) x[n-1] + x[n-2] + 2r\cos(\omega_0) y[n-1] - r^2 y[n-2] y[n]=x[n]−2cos(ω0)x[n−1]+x[n−2]+2rcos(ω0)y[n−1]−r2y[n−2]

滤波器系数计算式为：

b 0 = 1 b 1 = − 2 cos ⁡ ( ω 0 ) b 2 = 1 a 1 = 2 r cos ⁡ ( ω 0 ) a 2 = − r 2 \begin{aligned} b_0 &= 1 \\ b_1 &= -2\cos(\omega_0) \\ b_2 &= 1 \\ a_1 &= 2r\cos(\omega_0) \\ a_2 &= -r^2 \end{aligned} b0b1b2a1a2=1=−2cos(ω0)=1=2rcos(ω0)=−r2

参数 r r r 用于控制陷波的带宽，通常选择接近但小于 1 的数值，例如 0.9 至 0.99 之间的数值。陷波滤波器的 Q Q Q 值与参数 r r r 存在如下关系：

Q ≈ π f 0 T 1 − r Q \approx \frac{\pi f_0 T}{1 - r} Q≈1−rπf0T

其中 T T T 为采样周期。

对于数字陷波滤波器，若要在标准化频率 Ω 0 = ω 0 T \Omega_0 = \omega_0 T Ω0=ω0T 处实现陷波，其零点在单位圆上的角度为 Ω 0 \Omega_0 Ω0，对应的 z z z 平面位置为：

z 0 = e j Ω 0 , z 0 ∗ = e − j Ω 0 z_0 = e^{j\Omega_0}, \quad z_0^* = e^{-j\Omega_0} z0=ejΩ0,z0∗=e−jΩ0

而极点则位于：

p 0 = r e j Ω 0 , p 0 ∗ = r e − j Ω 0 p_0 = re^{j\Omega_0}, \quad p_0^* = re^{-j\Omega_0} p0=rejΩ0,p0∗=re−jΩ0

由多项式因式分解，可得系统函数：

H ( z ) = ( z − e j Ω 0 ) ( z − e − j Ω 0 ) ( z − r e j Ω 0 ) ( z − r e − j Ω 0 ) H(z) = \frac{(z - e^{j\Omega_0})(z - e^{-j\Omega_0})}{(z - re^{j\Omega_0})(z - re^{-j\Omega_0})} H(z)=(z−rejΩ0)(z−re−jΩ0)(z−ejΩ0)(z−e−jΩ0)

5. 设计方法

设计陷波滤波器时，需确定以下参数：

  1. 陷波频率 f 0 f_0 f0
  2. 陷波带宽或 Q Q Q 值
  3. 通带区域的波动要求
  4. 陷波深度要求

5.1 双 T 陷波滤波器设计

双 T 网络是实现陷波滤波器的经典结构，其电路参数计算式如下：

R 1 = R 2 = R R 3 = R 2 C 1 = C 2 = C C 3 = 2 C \begin{aligned} R_1 &= R_2 = R \\ R_3 &= \frac{R}{2} \\ C_1 &= C_2 = C \\ C_3 &= 2C \end{aligned} R1R3C1C3=R2=R=2R=C2=C=2C

中心频率由下式确定：

f 0 = 1 2 π R C f_0 = \frac{1}{2\pi RC} f0=2πRC1

对于给定的中心频率与电阻值，可计算所需的电容值：

C = 1 2 π f 0 R C = \frac{1}{2\pi f_0 R} C=2πf0R1

通过引入反馈因子 β \beta β，双 T 网络的 Q Q Q 值可调整为：

Q = 1 3 ( 1 − β ) Q = \frac{1}{3(1 - \beta)} Q=3(1−β)1

其中 β \beta β 是反馈因子，取值范围通常在 0.5 到 1 之间。

5.2 RLC 陷波滤波器设计

对于 RLC 陷波电路，元件参数值的计算公式为：

L = R 2 π f 0 Q , C = Q 2 π f 0 R L = \frac{R}{2\pi f_0 Q}, \quad C = \frac{Q}{2\pi f_0 R} L=2πf0QR,C=2πf0RQ

其中 R R R 是负载电阻或源电阻。

对于给定的陷波频率 f 0 f_0 f0、 Q Q Q 值与阻抗水平 R R R，完整的 RLC 并联陷波网络的传递函数为：

H ( s ) = s L R + s L + 1 s C = s 2 L C 1 + s 2 L C + s R C H(s) = \frac{sL}{R + sL + \frac{1}{sC}} = \frac{s^2 LC}{1 + s^2 LC + sRC} H(s)=R+sL+sC1sL=1+s2LC+sRCs2LC

简化后可得：

H ( s ) = s 2 s 2 + s R C + 1 L C H(s) = \frac{s^2}{s^2 + \frac{s}{RC} + \frac{1}{LC}} H(s)=s2+RCs+LC1s2

将分母标准化为 s 2 + ω 0 Q s + ω 0 2 s^2 + \frac{\omega_0}{Q} s + \omega_0^2 s2+Qω0s+ω02 的形式，可得：

1 R C = ω 0 Q , 1 L C = ω 0 2 \frac{1}{RC} = \frac{\omega_0}{Q}, \quad \frac{1}{LC} = \omega_0^2 RC1=Qω0,LC1=ω02

求解可得电感 L L L 与电容 C C C 的参数值：

L = R ω 0 Q = R 2 π f 0 Q , C = Q ω 0 R = Q 2 π f 0 R L = \frac{R}{\omega_0 Q} = \frac{R}{2\pi f_0 Q}, \quad C = \frac{Q}{\omega_0 R} = \frac{Q}{2\pi f_0 R} L=ω0QR=2πf0QR,C=ω0RQ=2πf0RQ

5.3 数字陷波滤波器设计

数字陷波滤波器的设计流程包含以下步骤：

  1. 确定需要滤除的目标频率 f 0 f_0 f0 与采样频率 f s f_s fs，计算采样周期 T = 1 f s T = \frac{1}{f_s} T=fs1
  2. 根据系统对带宽的要求，选取参数 r r r 的取值
  3. 计算数字角频率 ω 0 = 2 π f 0 T \omega_0 = 2\pi f_0 T ω0=2πf0T
  4. 依据系数计算公式确定差分方程的各项系数
  5. 采用直接型 II 结构实现滤波器的离散化运算

6. 频率响应分析

以标准二阶模拟陷波滤波器为分析对象，其传递函数为：

H ( s ) = s 2 + ω 0 2 s 2 + ω 0 Q s + ω 0 2 H(s) = \frac{s^2 + \omega_0^2}{s^2 + \frac{\omega_0}{Q} s + \omega_0^2} H(s)=s2+Qω0s+ω02s2+ω02

6.1 幅频响应特性

引入归一化频率 Ω = ω ω 0 \Omega = \frac{\omega}{\omega_0} Ω=ω0ω，则幅频响应可重写为：

∣ H ( j ω ) ∣ = ∣ H ( j Ω ω 0 ) ∣ = ∣ Ω 2 − 1 ∣ ( Ω 2 − 1 ) 2 + ( Ω Q ) 2 |H(j\omega)| = |H(j\Omega\omega_0)| = \frac{|\Omega^2 - 1|}{\sqrt{(\Omega^2 - 1)^2 + \left(\frac{\Omega}{Q}\right)^2}} ∣H(jω)∣=∣H(jΩω0)∣=(Ω2−1)2+(QΩ)2 ∣Ω2−1∣

对不同频率区间的幅频响应进行分析：

  1. 当 ω ≪ ω 0 \omega \ll \omega_0 ω≪ω0 时， Ω ≪ 1 \Omega \ll 1 Ω≪1，幅频响应近似为 ∣ H ( j ω ) ∣ ≈ 1 |H(j\omega)| \approx 1 ∣H(jω)∣≈1
  2. 当 ω ≫ ω 0 \omega \gg \omega_0 ω≫ω0 时， Ω ≫ 1 \Omega \gg 1 Ω≫1，幅频响应近似为 ∣ H ( j ω ) ∣ ≈ 1 |H(j\omega)| \approx 1 ∣H(jω)∣≈1
  3. 当 ω = ω 0 ± δ ω \omega = \omega_0 \pm \delta\omega ω=ω0±δω（ δ ω ≪ ω 0 \delta\omega \ll \omega_0 δω≪ω0）时，通过泰勒展开可得近似表达式：
    ∣ H ( j ( ω 0 ± δ ω ) ) ∣ ≈ 2 Q ∣ δ ω ∣ ω 0 4 Q 2 ( δ ω ω 0 ) 2 + 1 |H(j(\omega_0 \pm \delta\omega))| \approx \frac{2Q|\delta\omega|}{\omega_0\sqrt{4Q^2 \left(\frac{\delta\omega}{\omega_0}\right)^2 + 1}} ∣H(j(ω0±δω))∣≈ω04Q2(ω0δω)2+1 2Q∣δω∣
    当 δ ω \delta\omega δω 数值极小时，可进一步近似为：
    ∣ H ( j ( ω 0 ± δ ω ) ) ∣ ≈ 2 Q ∣ δ ω ∣ ω 0 |H(j(\omega_0 \pm \delta\omega))| \approx \frac{2Q|\delta\omega|}{\omega_0} ∣H(j(ω0±δω))∣≈ω02Q∣δω∣

上述分析表明，陷波滤波器仅在陷波频率附近产生明显的信号衰减，而在远离陷波频率的区域，其增益趋近于 1。

6.2 相位响应特性

陷波滤波器的相位响应表达式为：

ϕ ( ω ) = arg ⁡ [ H ( j ω ) ] = tan ⁡ − 1 ( Im [ H ( j ω ) ] Re [ H ( j ω ) ] ) \phi(\omega) = \arg[H(j\omega)] = \tan^{-1}\left(\frac{\text{Im}[H(j\omega)]}{\text{Re}[H(j\omega)]}\right) ϕ(ω)=arg[H(jω)]=tan−1(Re[H(jω)]Im[H(jω)])

对于标准二阶陷波滤波器，将 s = j ω s = j\omega s=jω 代入传递函数并分离实部与虚部：

Re [ H ( j ω ) ] = ( ω 2 − ω 0 2 ) 2 ( ω 2 − ω 0 2 ) 2 + ( ω 0 ω Q ) 2 \text{Re}[H(j\omega)] = \frac{(\omega^2 - \omega_0^2)^2}{(\omega^2 - \omega_0^2)^2 + \left(\frac{\omega_0\omega}{Q}\right)^2} Re[H(jω)]=(ω2−ω02)2+(Qω0ω)2(ω2−ω02)2

Im [ H ( j ω ) ] = ( ω 2 − ω 0 2 ) ( ω 0 ω Q ) ( ω 2 − ω 0 2 ) 2 + ( ω 0 ω Q ) 2 \text{Im}[H(j\omega)] = \frac{(\omega^2 - \omega_0^2)\left(\frac{\omega_0\omega}{Q}\right)}{(\omega^2 - \omega_0^2)^2 + \left(\frac{\omega_0\omega}{Q}\right)^2} Im[H(jω)]=(ω2−ω02)2+(Qω0ω)2(ω2−ω02)(Qω0ω)

相位响应表达式可简化为：

ϕ ( ω ) = tan ⁡ − 1 ( ω 0 ω Q ( ω 2 − ω 0 2 ) ) \phi(\omega) = \tan^{-1}\left(\frac{\omega_0\omega}{Q(\omega^2 - \omega_0^2)}\right) ϕ(ω)=tan−1(Q(ω2−ω02)ω0ω)

对相位响应特性的分析结论如下：

  1. 当 ω < ω 0 \omega < \omega_0 ω<ω0 时， ω 2 − ω 0 2 < 0 \omega^2 - \omega_0^2 < 0 ω2−ω02<0， ϕ ( ω ) ∈ ( − π 2 , 0 ) \phi(\omega) \in (-\frac{\pi}{2}, 0) ϕ(ω)∈(−2π,0)
  2. 当 ω = ω 0 \omega = \omega_0 ω=ω0 时，分母为 0，相位出现不连续现象
  3. 当 ω > ω 0 \omega > \omega_0 ω>ω0 时， ω 2 − ω 0 2 > 0 \omega^2 - \omega_0^2 > 0 ω2−ω02>0， ϕ ( ω ) ∈ ( 0 , π 2 ) \phi(\omega) \in (0, \frac{\pi}{2}) ϕ(ω)∈(0,2π)

在陷波频率处会出现 180 度的相位突变，该现象的产生原因是传递函数的零点位于虚轴上。在陷波频率以下的频段，相位趋近于 0 度；而在陷波频率以上的频段，相位趋近于 180 度。

6.3 群延迟特性

群延迟用于描述信号不同频率成分的传输延迟，表达式为：

τ g ( ω ) = − d ϕ ( ω ) d ω \tau_g(\omega) = -\frac{d\phi(\omega)}{d\omega} τg(ω)=−dωdϕ(ω)

对陷波滤波器的相位响应求导，可得群延迟的计算表达式，该参数对于分析陷波滤波器对波形保真度的影响具有重要意义。

7. 时域响应分析

陷波滤波器的时域响应可通过对传递函数进行拉普拉斯逆变换得到，以标准二阶模拟陷波滤波器为分析对象，其传递函数可改写为：

H ( s ) = 1 − ω 0 Q s s 2 + ω 0 Q s + ω 0 2 H(s) = 1 - \frac{\frac{\omega_0}{Q} s}{s^2 + \frac{\omega_0}{Q} s + \omega_0^2} H(s)=1−s2+Qω0s+ω02Qω0s

令 α = ω 0 2 Q \alpha = \frac{\omega_0}{2Q} α=2Qω0 且 ω d = ω 0 1 − 1 4 Q 2 \omega_d = \omega_0\sqrt{1 - \frac{1}{4Q^2}} ωd=ω01−4Q21 （假设 Q > 1 2 Q > \frac{1}{2} Q>21），则传递函数可进一步改写为：

H ( s ) = 1 − 2 α s ( s + α ) 2 + ω d 2 H(s) = 1 - \frac{2\alpha s}{(s + \alpha)^2 + \omega_d^2} H(s)=1−(s+α)2+ωd22αs

利用拉普拉斯变换对，可得单位脉冲响应：

h ( t ) = δ ( t ) − 2 α e − α t sin ⁡ ( ω d t ) ω d = δ ( t ) − 1 Q 1 − 1 4 Q 2 e − ω 0 t 2 Q sin ⁡ ( ω 0 t 1 − 1 4 Q 2 ) \begin{aligned} h(t) &= \delta(t) - 2\alpha e^{-\alpha t}\frac{\sin(\omega_d t)}{\omega_d} \\ &= \delta(t) - \frac{1}{Q\sqrt{1 - \frac{1}{4Q^2}}} e^{-\frac{\omega_0 t}{2Q}} \sin\left(\omega_0 t\sqrt{1 - \frac{1}{4Q^2}}\right) \end{aligned} h(t)=δ(t)−2αe−αtωdsin(ωdt)=δ(t)−Q1−4Q21 1e−2Qω0tsin(ω0t1−4Q21 )

其中 δ ( t ) \delta(t) δ(t) 为单位脉冲函数。

该响应包含两部分：即时脉冲与衰减正弦波。当 Q Q Q 值较大时，衰减速度较慢，会产生较长时间的"振铃"效应。对于高 Q Q Q 值的情况，可近似为：

h ( t ) ≈ δ ( t ) − 1 Q e − ω 0 t 2 Q sin ⁡ ( ω 0 t ) h(t) \approx \delta(t) - \frac{1}{Q} e^{-\frac{\omega_0 t}{2Q}} \sin(\omega_0 t) h(t)≈δ(t)−Q1e−2Qω0tsin(ω0t)

对于任意输入信号 x ( t ) x(t) x(t)，输出 y ( t ) y(t) y(t) 可通过卷积运算得到：

y ( t ) = ( x ∗ h ) ( t ) = ∫ − ∞ ∞ x ( τ ) h ( t − τ ) d τ = x ( t ) − 1 Q 1 − 1 4 Q 2 ∫ − ∞ ∞ x ( τ ) e − ω 0 ( t − τ ) 2 Q sin ⁡ ( ω 0 ( t − τ ) 1 − 1 4 Q 2 ) d τ \begin{aligned} y(t) &= (x * h)(t) \\ &= \int_{-\infty}^{\infty} x(\tau) h(t - \tau) d\tau \\ &= x(t) - \frac{1}{Q\sqrt{1 - \frac{1}{4Q^2}}} \int_{-\infty}^{\infty} x(\tau) e^{-\frac{\omega_0 (t - \tau)}{2Q}} \sin\left(\omega_0 (t - \tau)\sqrt{1 - \frac{1}{4Q^2}}\right) d\tau \end{aligned} y(t)=(x∗h)(t)=∫−∞∞x(τ)h(t−τ)dτ=x(t)−Q1−4Q21 1∫−∞∞x(τ)e−2Qω0(t−τ)sin(ω0(t−τ)1−4Q21 )dτ

当输入为单位阶跃函数 x ( t ) = u ( t ) x(t) = u(t) x(t)=u(t) 时，通过变量替换与积分运算，可得阶跃响应表达式，该表达式包含初始瞬态响应与最终稳态响应两部分。

8. 应用场景

陷波滤波器的主要用途是消除特定且已知的周期性干扰信号，典型应用场景如下：

  1. 消除工频干扰：在生物电信号采集（如心电图 ECG、脑电图 EEG）或精密测量等领域，50Hz 或 60Hz 的市电及其谐波是主要的干扰源，使用中心频率为 50Hz 或 60Hz 的陷波滤波器，可有效去除该类干扰信号。
  2. 音频处理：用于消除音频录制过程中产生的特定频率哼声或啸叫声。
  3. 通信系统：用于抑制特定频率的干扰信号或载波信号。
  4. 振动分析：用于消除旋转机械（如电机）在固定转速下产生的周期性振动信号。
  5. 仪器仪表：在精密测量设备中应用，可有效提高测量信号的信噪比。

9. 与其他滤波器的对比

陷波滤波器与常见滤波器类型的特性对比如下表所示：

滤波器类型 功能 与陷波滤波器的区别
低通滤波器 仅允许低频信号通过，阻止高频信号通过 对较宽频带内的信号产生影响（所有高于截止频率的信号成分），而非仅针对单个频率信号
高通滤波器 仅允许高频信号通过，阻止低频信号通过 对较宽频带内的信号产生影响（所有低于截止频率的信号成分）
带阻滤波器 阻止特定频带范围内的信号通过 陷波滤波器是带阻滤波器的特例，带阻滤波器的阻带通常较宽，而陷波滤波器的阻带较窄
带通滤波器 仅允许特定频带范围内的信号通过 功能与陷波滤波器完全相反

旋转的艺术 于2024-12-25 19:41:04 发布

陷波滤波器设计

陷波滤波器（Notch Filter）属于带阻滤波器（Band-Stop Filter），其设计目的是在特定中心频率处对信号进行显著衰减，而在其他频率范围内对信号基本无影响。

1. 常见连续陷波滤波器为二阶结构，其传递函数定义如下：

H ( s ) = s 2 + ω 0 2 s 2 + ω 0 Q s + ω 0 2 H(s) = \frac{s^2 + \omega_0^2}{s^2 + \frac{\omega_0}{Q} s + \omega_0^2} H(s)=s2+Qω0s+ω02s2+ω02

参数说明：

  • H ( s ) H(s) H(s)：滤波器的传递函数。

  • s s s：拉普拉斯变换中的复频率变量， s = σ + j ω s = \sigma + j\omega s=σ+jω。

  • ω 0 \omega_0 ω0：带阻中心角频率，单位为弧度每秒（rad/s）。

  • Q Q Q：品质因数，用于决定滤波器的带宽。 Q Q Q 值越高，对应的带宽越窄。

1.1 零极点位置分析

零点（Zeros）：

带阻滤波器传递函数的分子部分满足以下方程：

s 2 + ω 0 2 = 0 ⇒ s = ± j ω 0 s^2 + \omega_0^2 = 0 \quad \Rightarrow \quad s = \pm j\omega_0 s2+ω02=0⇒s=±jω0

即滤波器在 s = j ω 0 s = j\omega_0 s=jω0 和 s = − j ω 0 s = -j\omega_0 s=−jω0 处存在两个零点。

1.2 极点（Poles）：

传递函数的分母部分满足以下方程：

s 2 + ω 0 Q s + ω 0 2 = 0 s^2 + \frac{\omega_0}{Q} s + \omega_0^2 = 0 s2+Qω0s+ω02=0

求解上述二次方程，可得：

s = − ω 0 Q ± ( ω 0 Q ) 2 − 4 ⋅ 1 ⋅ ω 0 2 2 = − ω 0 2 Q ± j ω 0 1 − 1 4 Q 2 \begin{aligned} s &= \frac{-\frac{\omega_0}{Q} \pm \sqrt{\left(\frac{\omega_0}{Q}\right)^2 - 4 \cdot 1 \cdot \omega_0^2}}{2} \\ &= -\frac{\omega_0}{2Q} \pm j\omega_0 \sqrt{1 - \frac{1}{4Q^2}} \end{aligned} s=2−Qω0±(Qω0)2−4⋅1⋅ω02 =−2Qω0±jω01−4Q21

即滤波器在 s = − ω 0 2 Q ± j ω 0 1 − 1 4 Q 2 s = -\frac{\omega_0}{2Q} \pm j\omega_0 \sqrt{1 - \frac{1}{4Q^2}} s=−2Qω0±jω01−4Q21 处存在两个极点。

1.3 频率响应特性

在带阻中心频率 ω = ω 0 \omega = \omega_0 ω=ω0 处，传递函数的增益趋近于零，实现对目标信号的抑制：

H ( j ω 0 ) = 0 H(j\omega_0) = 0 H(jω0)=0

1.4 频率响应分析

频率响应描述滤波器对不同频率信号的增益与相位变化规律。通过传递函数可推导滤波器的频率响应，并分析零极点对频率响应的影响。

1.4.1 频率响应的数学表达
连续时间滤波器

将 s = j ω s = j\omega s=jω 代入连续时间传递函数，可得：

H ( j ω ) = ( j ω ) 2 + ω 0 2 ( j ω ) 2 + ω 0 Q ( j ω ) + ω 0 2 = − ω 2 + ω 0 2 − ω 2 + j ω 0 ω Q + ω 0 2 \begin{aligned} H(j\omega) &= \frac{(j\omega)^2 + \omega_0^2}{(j\omega)^2 + \frac{\omega_0}{Q} (j\omega) + \omega_0^2} \\[1em] &= \frac{-\omega^2 + \omega_0^2}{-\omega^2 + j\frac{\omega_0 \omega}{Q} + \omega_0^2} \end{aligned} H(jω)=(jω)2+Qω0(jω)+ω02(jω)2+ω02=−ω2+jQω0ω+ω02−ω2+ω02

离散时间滤波器

将 z = e j Ω z = e^{j\Omega} z=ejΩ 代入离散时间传递函数，可得：

H ( e j Ω ) = b 0 + b 1 e − j Ω + b 2 e − j 2 Ω 1 + a 1 e − j Ω + a 2 e − j 2 Ω H(e^{j\Omega}) = \frac{b_0 + b_1 e^{-j\Omega} + b_2 e^{-j2\Omega}}{1 + a_1 e^{-j\Omega} + a_2 e^{-j2\Omega}} H(ejΩ)=1+a1e−jΩ+a2e−j2Ωb0+b1e−jΩ+b2e−j2Ω

其中， Ω \Omega Ω 为数字频率，单位为弧度；在 ω = ω 0 \omega = \omega_0 ω=ω0 处，零点的存在形成陷波，使增益在此频率处显著降低。

1.4.2 零极点对频率响应的影响
零点的影响

  • 位置：零点位于单位圆上（数字滤波器）或虚轴上（模拟滤波器）。

  • 效果：在零点对应频率处，滤波器增益为零，理论上可实现信号的完全抑制。

  • 带阻中心频率：带阻滤波器的零点通常设置于带阻中心频率 ω 0 \omega_0 ω0 处，确保该频率处具有最小增益。

极点的影响

  • 位置：极点位于单位圆内（数字滤波器）或左半平面（模拟滤波器）。

  • 效果：极点与零点的接近程度决定滤波器的带宽与频率选择特性。极点越靠近单位圆或虚轴，带宽越窄，滤波器响应越尖锐。

  • 稳定性：极点必须位于单位圆内或左半平面，以保证滤波器的稳定性。

综合影响

  • 带宽：极点与零点的距离决定带阻滤波器的带宽。 Q Q Q 值越高，极点越靠近单位圆，带宽越窄。

  • 过渡带：极点位置影响滤波器过渡带的陡峭程度，极点越靠近零点，过渡带越陡峭。

  • 增益和相位：零极点的位置共同影响滤波器的整体增益与相位特性，决定滤波器在不同频率下的工作行为。

2. 双线性变换简介

双线性变换（Bilinear Transform）是一种将连续时间系统转换为离散时间系统的数学方法，其思想是通过非线性映射，将 s s s 域频率转换为 z z z 域频率。双线性变换的替换公式为：

s = 2 T ⋅ 1 − z − 1 1 + z − 1 s = \frac{2}{T} \cdot \frac{1 - z^{-1}}{1 + z^{-1}} s=T2⋅1+z−11−z−1

其中：

  • s s s：连续时间复频率变量。

  • z z z：离散时间复频率变量。

  • T T T：采样周期， T = 1 f s T = \frac{1}{f_s} T=fs1， f s f_s fs 为采样频率。

双线性变换的优点：

  • 避免频率混叠：通过频率预畸变处理，确保高频信号不会混叠至低频段。

  • 保持滤波器稳定性：当模拟滤波器稳定时，经双线性变换得到的数字滤波器同样稳定。

双线性变换的缺点：

  • 引入频率扭曲：由于非线性映射关系，频率响应会发生扭曲，且在高频区域该现象更为显著。

3. 频率扭曲的原因

双线性变换通过替换公式 s = 2 T ⋅ 1 − z − 1 1 + z − 1 s = \frac{2}{T} \cdot \frac{1 - z^{-1}}{1 + z^{-1}} s=T2⋅1+z−11−z−1 实现连续时间系统到离散时间系统的转换，该替换具有非线性特性，导致频率映射关系不一致，即产生频率扭曲。

频率扭曲的数学解释：

将 s = j ω s = j\omega s=jω 与 z = e j Ω z = e^{j\Omega} z=ejΩ（ Ω \Omega Ω 为数字频率，单位为弧度）代入替换公式，可得：

j ω = 2 T ⋅ 1 − e − j Ω 1 + e − j Ω = 2 T ⋅ j tan ⁡ ( Ω 2 ) j\omega = \frac{2}{T} \cdot \frac{1 - e^{-j\Omega}}{1 + e^{-j\Omega}} = \frac{2}{T} \cdot j \tan\left(\frac{\Omega}{2}\right) jω=T2⋅1+e−jΩ1−e−jΩ=T2⋅jtan(2Ω)

整理后得到：

ω = 2 T tan ⁡ ( Ω 2 ) \omega = \frac{2}{T} \tan\left(\frac{\Omega}{2}\right) ω=T2tan(2Ω)

由上式可知，连续时间模拟频率 ω \omega ω 与离散时间数字频率 Ω \Omega Ω 呈非线性关系，尤其当 Ω \Omega Ω 接近 π \pi π 时， ω \omega ω 会快速增大，从而引入频率扭曲。

4. 频率扭曲的影响

受双线性变换非线性特性的影响，模拟频率与数字频率的对应关系不再线性，这种扭曲会对滤波器设计产生不利影响，尤其当滤波器需在特定频率点（如中心频率）保持准确响应时。

具体影响包括：

  • 中心频率偏移：滤波器实际中心频率与设计频率存在偏差。

  • 带宽变化：滤波器实际带宽与设计要求不符。

  • 高频响应失真：滤波器在高频区域的响应与预期特性存在差异。

为确保数字滤波器在设计频率处具有准确响应，需采取针对性措施纠正或减小频率扭曲的影响。

5. 解决频率扭曲的方法

5.1 预畸变（Pre-Warping）

预畸变是解决双线性变换引入频率扭曲的主要方法，其思路是在应用双线性变换前，对设计频率进行预先调整，以抵消变换过程中产生的频率扭曲。

预畸变的基本步骤：

  1. 确定设计频率：选取滤波器需准确响应的关键频率 ω d \omega_d ωd（设计频率）。

  2. 计算预畸变频率：利用双线性变换的频率映射关系，将设计频率映射为模拟频率，公式如下：
    ω a = 2 T tan ⁡ ( ω d 2 ) \omega_a = \frac{2}{T} \tan\left(\frac{\omega_d}{2}\right) ωa=T2tan(2ωd)

    其中， ω a \omega_a ωa 为用于设计模拟滤波器的频率， ω d \omega_d ωd 为数字滤波器的设计频率。

  3. 设计模拟滤波器：基于预畸变后的频率 ω a \omega_a ωa 完成模拟滤波器设计。

  4. 应用双线性变换：将设计好的模拟滤波器传递函数转换为数字滤波器传递函数。

预畸变的数学依据：

通过选取 ω a \omega_a ωa，使双线性变换后数字滤波器的关键频率 ω d \omega_d ωd 与模拟滤波器的 ω a \omega_a ωa 准确对应，确保滤波器在 ω d \omega_d ωd 处具有设计预期的滤波特性。

5.2 使用其他离散化方法

除双线性变换外，冲激不变法（Impulse Invariance）、向前差分/向后差分方法等也可用于滤波器离散化。但此类方法各有优劣，在避免频率混叠方面的效果通常不及双线性变换，因此预畸变结合双线性变换是工程实践中的首选方案。

5.3 预畸变的数学推导

目标：

确保数字滤波器在设计频率 ω d \omega_d ωd 处具有准确响应。

已知关系：

ω a = 2 T tan ⁡ ( ω d 2 ) \omega_a = \frac{2}{T} \tan\left(\frac{\omega_d}{2}\right) ωa=T2tan(2ωd)

步骤：

  1. 选择设计频率 ω d \omega_d ωd：例如，设定滤波器在数字频率 ω d = ω design \omega_d = \omega_{\text{design}} ωd=ωdesign 处具有特定特性（如中心频率特性）。

  2. 计算预畸变频率 ω a \omega_a ωa：
    ω a = 2 T tan ⁡ ( ω d 2 ) = 2 f s tan ⁡ ( ω d 2 ) \omega_a = \frac{2}{T} \tan\left(\frac{\omega_d}{2}\right) = 2 f_s \tan\left(\frac{\omega_d}{2}\right) ωa=T2tan(2ωd)=2fstan(2ωd)

    其中， T = 1 f s T = \frac{1}{f_s} T=fs1。

  3. 设计模拟滤波器：基于预畸变后的频率 ω a \omega_a ωa 推导模拟滤波器传递函数 H ( s ) H(s) H(s)。

  4. 应用双线性变换：将 H ( s ) H(s) H(s) 转换为数字滤波器传递函数 H ( z ) H(z) H(z)，此时 H ( z ) H(z) H(z) 在 ω d \omega_d ωd 处具有准确响应。

6. 离散时间（数字）带阻滤波器传递函数

通过双线性变换方法，可将连续时间带阻滤波器转换为离散时间带阻滤波器。标准二阶数字带阻滤波器的传递函数为：

H ( z ) = b 0 + b 1 z − 1 + b 2 z − 2 1 + a 1 z − 1 + a 2 z − 2 H(z) = \frac{b_0 + b_1 z^{-1} + b_2 z^{-2}}{1 + a_1 z^{-1} + a_2 z^{-2}} H(z)=1+a1z−1+a2z−2b0+b1z−1+b2z−2

滤波器系数计算

给定采样频率 f s f_s fs、带阻中心频率 f 0 f_0 f0 和品质因数 Q Q Q，滤波器系数的计算步骤如下：

  1. 计算归一化角频率：
    ω 0 = 2 π f 0 f s \omega_0 = \frac{2\pi f_0}{f_s} ω0=fs2πf0

  2. 计算中间变量：
    α = sin ⁡ ( ω 0 ) 2 Q cos ⁡ ( ω 0 ) = cos ⁡ ( ω 0 ) \begin{aligned} \alpha &= \frac{\sin(\omega_0)}{2Q} \\ \cos(\omega_0) &= \cos(\omega_0) \end{aligned} αcos(ω0)=2Qsin(ω0)=cos(ω0)

  3. 计算双二阶IIR滤波器的未归一化系数：
    b 0 = 1 b 1 = − 2 cos ⁡ ( ω 0 ) b 2 = 1 a 0 = 1 + α a 1 = − 2 cos ⁡ ( ω 0 ) a 2 = 1 − α \begin{aligned} b_0 &= 1 \\ b_1 &= -2 \cos(\omega_0) \\ b_2 &= 1 \\ a_0 &= 1 + \alpha \\ a_1 &= -2 \cos(\omega_0) \\ a_2 &= 1 - \alpha \end{aligned} b0b1b2a0a1a2=1=−2cos(ω0)=1=1+α=−2cos(ω0)=1−α

  4. 系数归一化：将所有系数除以 a 0 a_0 a0，使传递函数标准化：
    b 0 ′ = b 0 a 0 b 1 ′ = b 1 a 0 b 2 ′ = b 2 a 0 a 1 ′ = a 1 a 0 a 2 ′ = a 2 a 0 \begin{aligned} b_0' &= \frac{b_0}{a_0} \\ b_1' &= \frac{b_1}{a_0} \\ b_2' &= \frac{b_2}{a_0} \\ a_1' &= \frac{a_1}{a_0} \\ a_2' &= \frac{a_2}{a_0} \end{aligned} b0′b1′b2′a1′a2′=a0b0=a0b1=a0b2=a0a1=a0a2

最终，离散带阻滤波器的传递函数为：

H ( z ) = b 0 ′ + b 1 ′ z − 1 + b 2 ′ z − 2 1 + a 1 ′ z − 1 + a 2 ′ z − 2 H(z) = \frac{b_0' + b_1' z^{-1} + b_2' z^{-2}}{1 + a_1' z^{-1} + a_2' z^{-2}} H(z)=1+a1′z−1+a2′z−2b0′+b1′z−1+b2′z−2

陷波滤波器Simulink仿真

陷波滤波器初始化框图如下图所示：

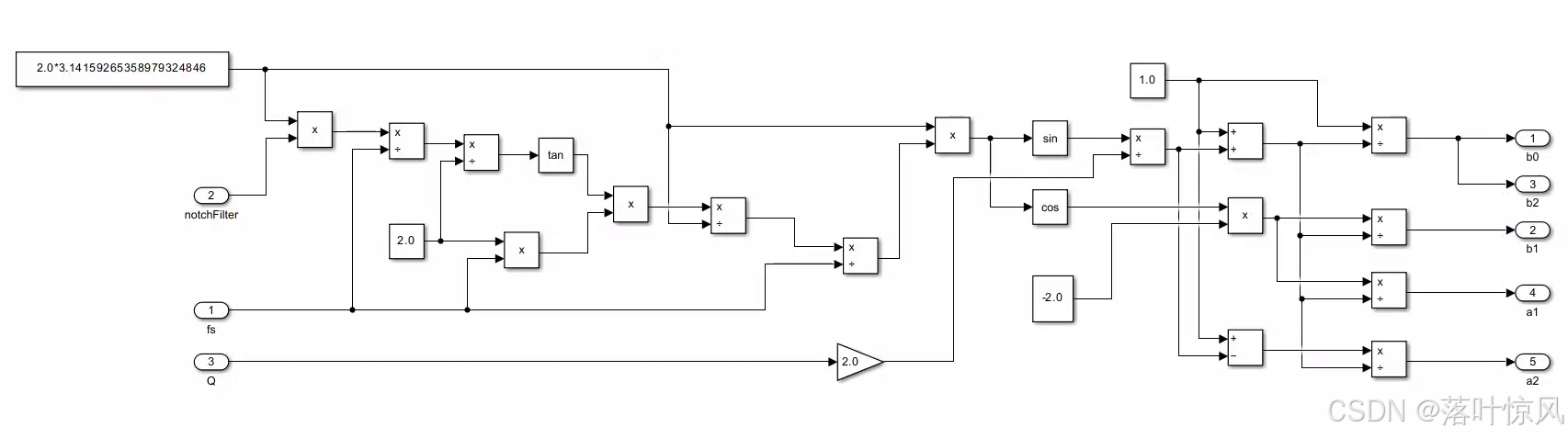
陷波滤波器处理框图如下图所示：

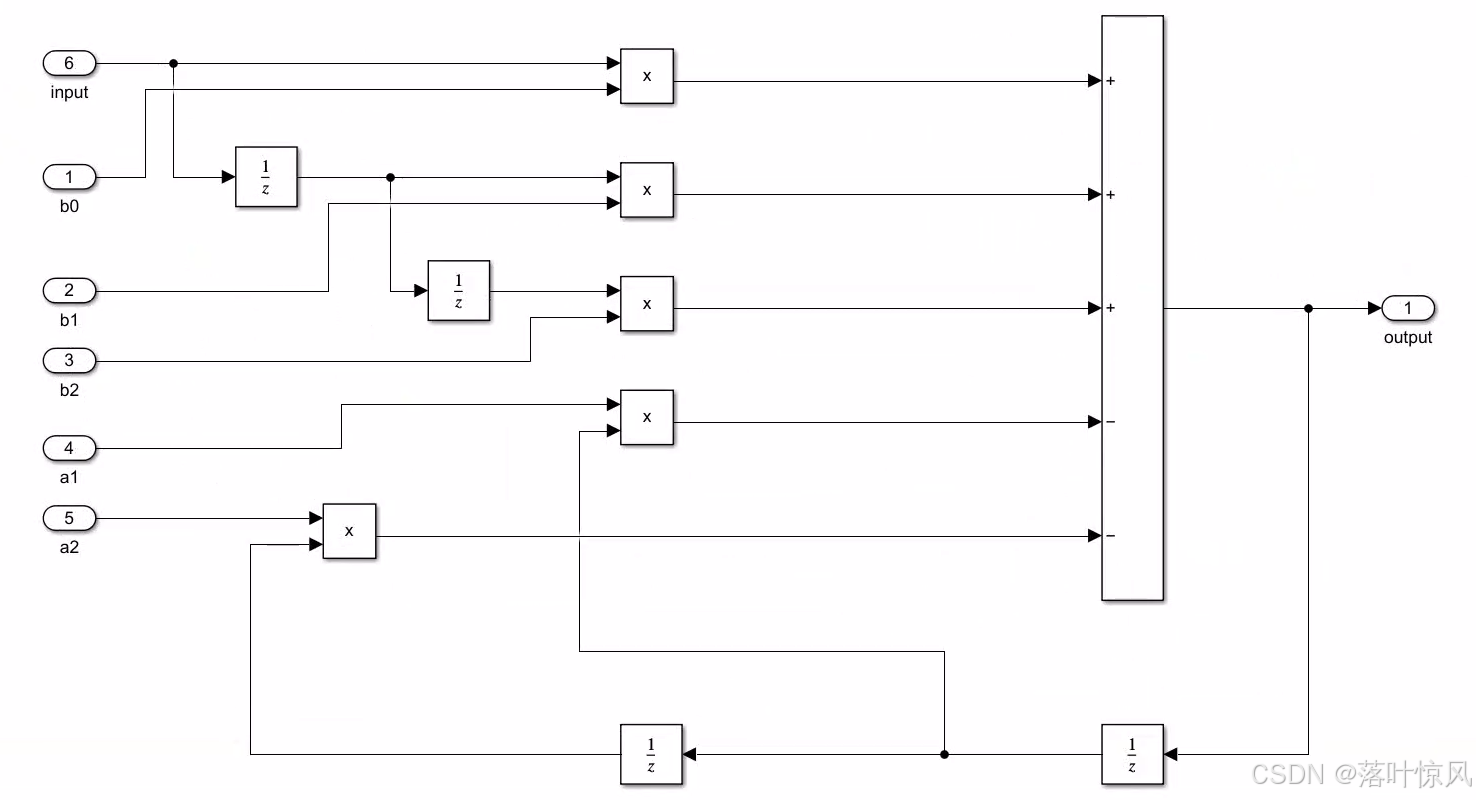
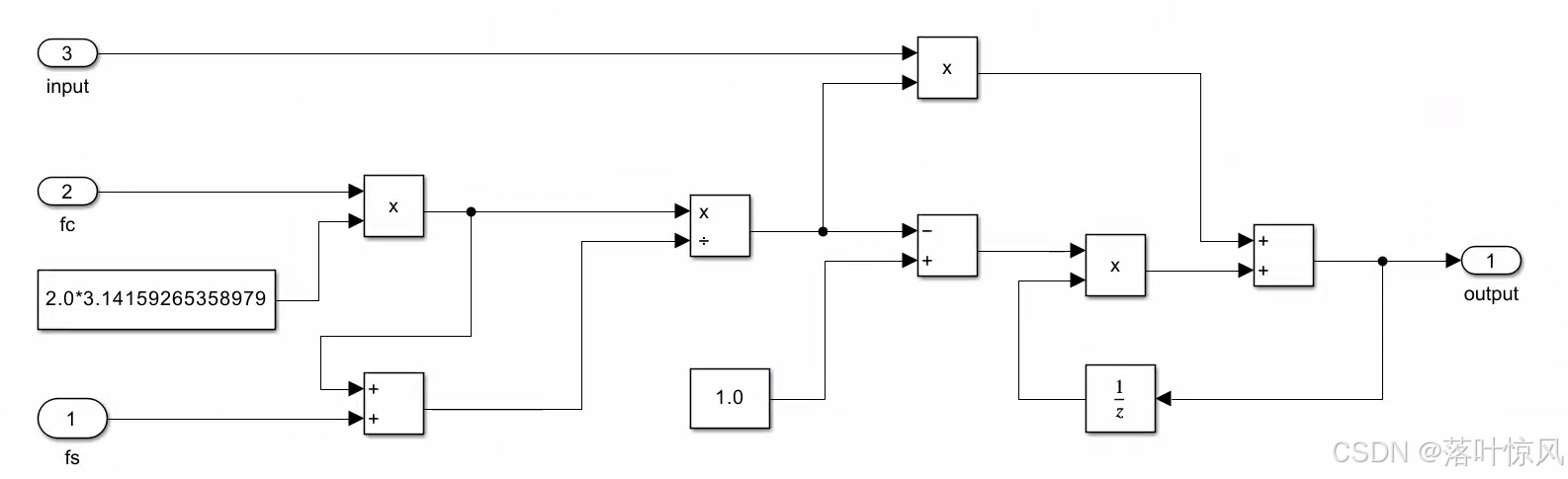
低通滤波器框图：

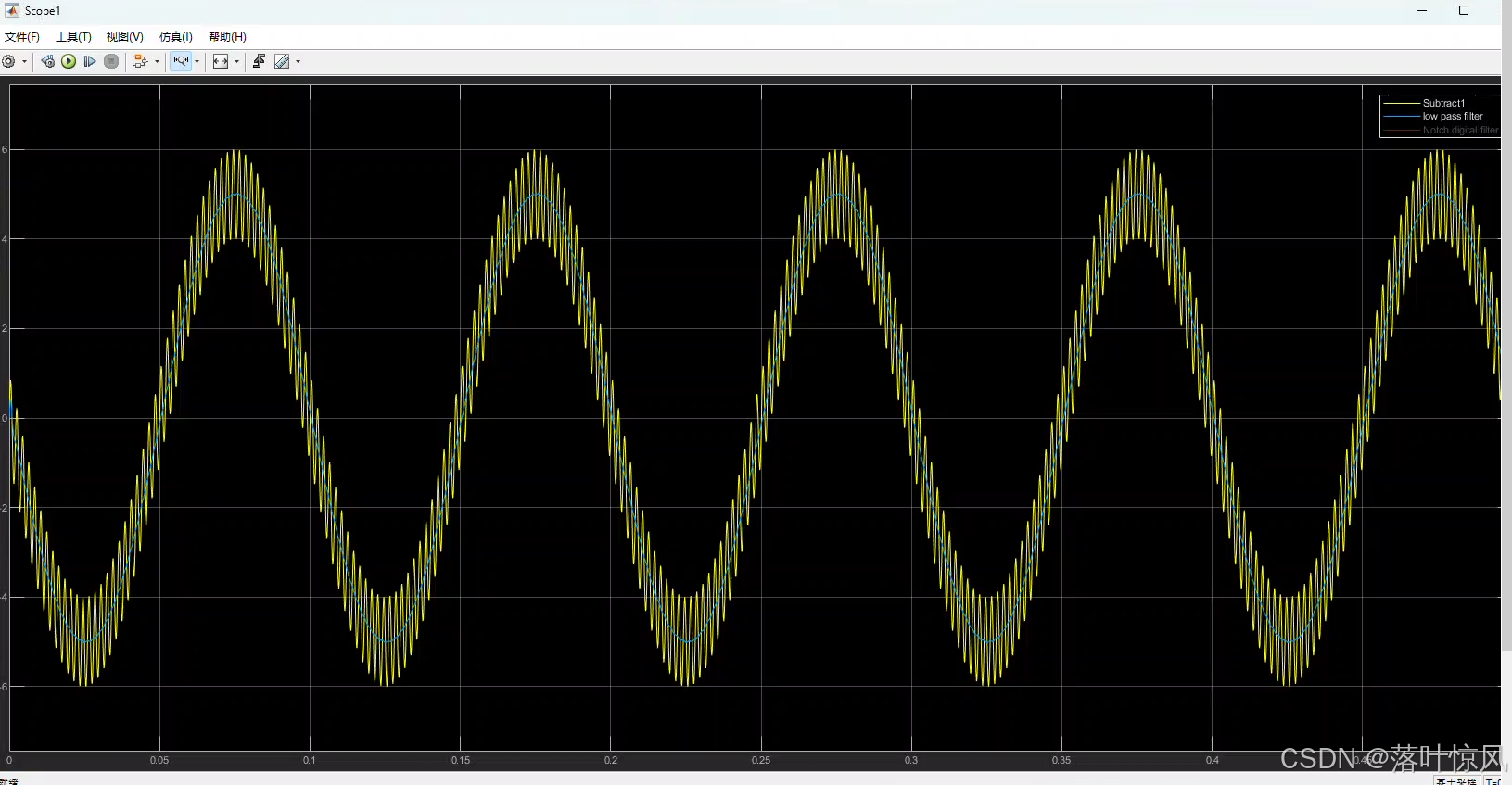
仿真条件及结果

设定采样频率 25000 Hz 25000\ \text{Hz} 25000 Hz、滤波器中心频率 500 Hz 500\ \text{Hz} 500 Hz、品质因数 20 20 20，低通滤波器截止频率 2000 Hz 2000\ \text{Hz} 2000 Hz，不同测试波形的仿真结果如下：

  • 测试波形为 10 Hz + 500 Hz 10\ \text{Hz}+500\ \text{Hz} 10 Hz+500 Hz 叠加信号的仿真波形：

  • 测试波形为 10 Hz + 600 Hz 10\ \text{Hz}+600\ \text{Hz} 10 Hz+600 Hz 叠加信号的仿真波形：

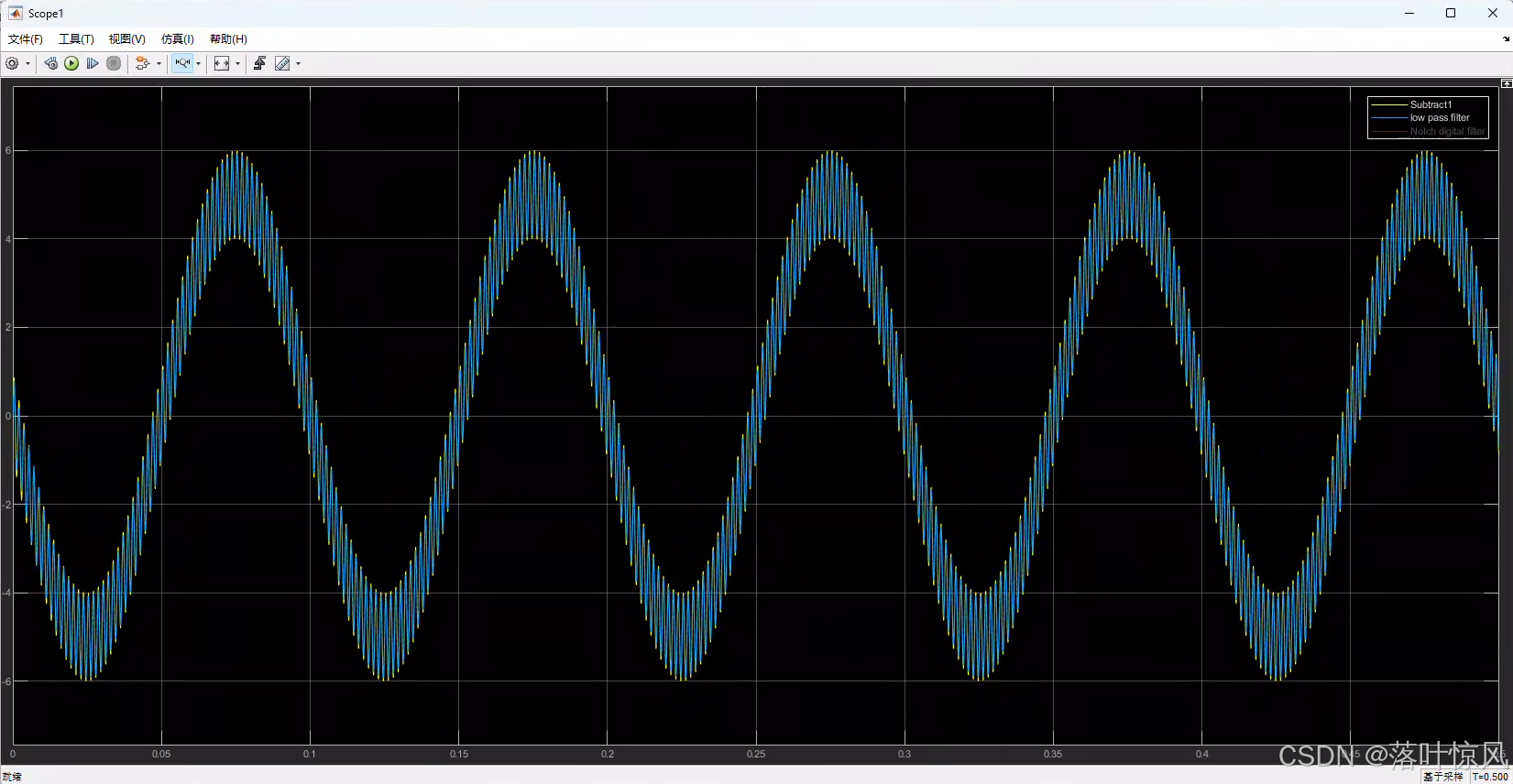
  • 测试波形为 10 Hz + 400 Hz 10\ \text{Hz}+400\ \text{Hz} 10 Hz+400 Hz 叠加信号的仿真波形：

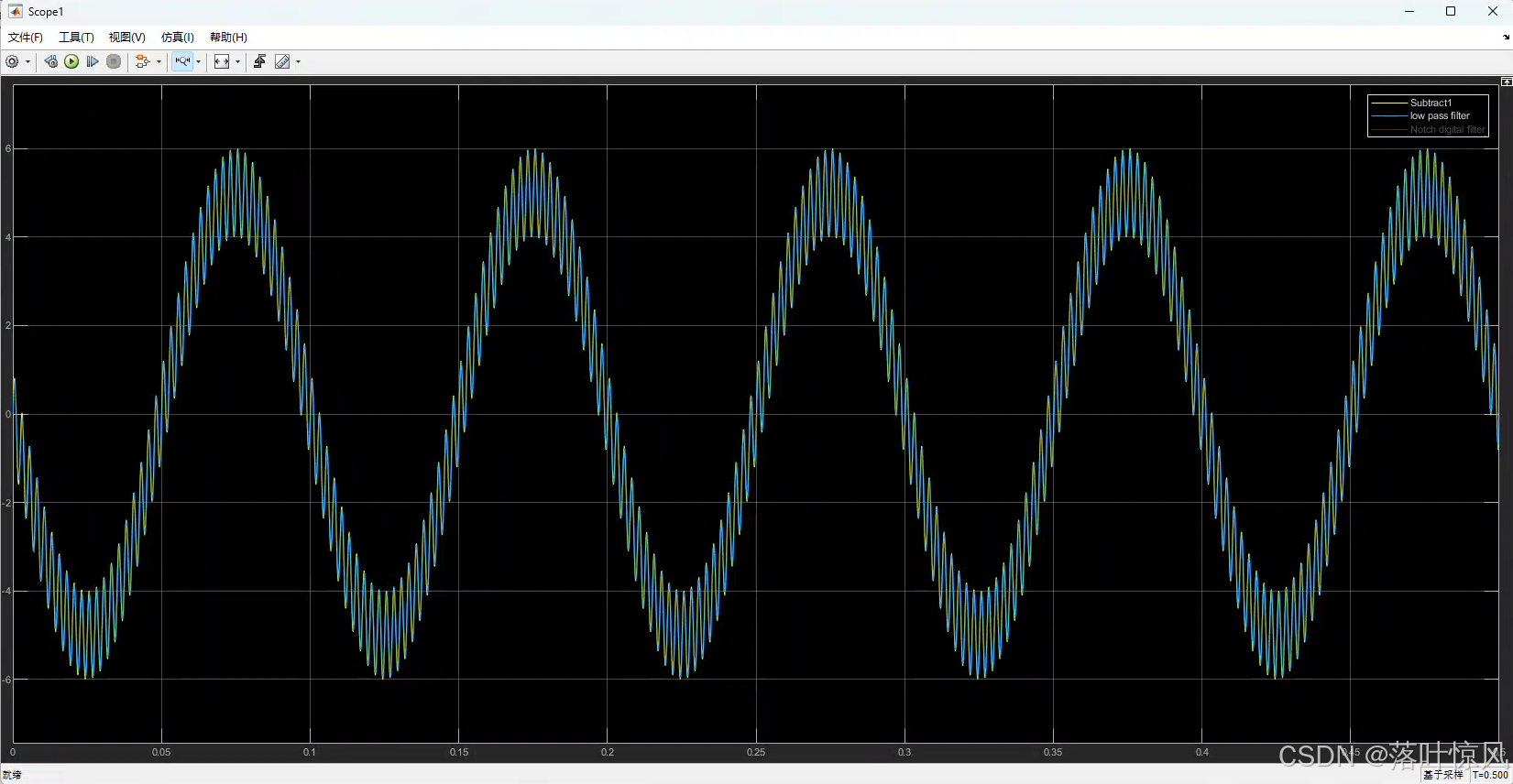
附录：滤波器设计与实现示例

以下为基于双二阶IIR结构实现的数字带阻滤波器C语言示例代码，采用预畸变方法校正频率扭曲。

c 复制代码 
#include <stdio.h>
#include <math.h>

// 定义滤波器结构体
typedef struct {
    // 滤波器系数
    double b0, b1, b2;
    double a1, a2;
    // 滤波器状态
    double x1, x2; // 前两个输入样本
    double y1, y2; // 前两个输出样本
} Biquad;

// 初始化带阻滤波器，应用预畸变
void initBandStopFilter(Biquad *filter, double fs, double notchFreq, double Q) {
    // 设计频率预畸变
    double omega_d = 2.0 * M_PI * notchFreq / fs; // 设计数字频率
    double omega_a = 2.0 * tan(omega_d / 2.0);    // 预畸变后的模拟频率

    // 计算中间变量
    double alpha = sin(omega_a) / (2.0 * Q);
    double cosw = cos(omega_a);

    // 计算未归一化滤波器系数
    double b0 = 1.0;
    double b1_coeff = -2.0 * cosw;
    double b2 = 1.0;
    double a0 = 1.0 + alpha;
    double a1 = -2.0 * cosw;
    double a2 = 1.0 - alpha;

    // 归一化滤波器系数
    filter->b0 = b0 / a0;
    filter->b1 = b1_coeff / a0;
    filter->b2 = b2 / a0;
    filter->a1 = a1 / a0;
    filter->a2 = a2 / a0;

    // 初始化状态
    filter->x1 = 0.0;
    filter->x2 = 0.0;
    filter->y1 = 0.0;
    filter->y2 = 0.0;
}

// 处理单个样本
double processSample(Biquad *filter, double input) {
    double output = filter->b0 * input + filter->b1 * filter->x1 + filter->b2 * filter->x2
                    - filter->a1 * filter->y1 - filter->a2 * filter->y2;

    // 更新状态
    filter->x2 = filter->x1;
    filter->x1 = input;
    filter->y2 = filter->y1;
    filter->y1 = output;

    return output;
}

int main() {
    // 示例参数
    double fs = 48000.0;           // 采样率 48 kHz
    double notchFreq = 1000.0;     // 带阻中心频率 1 kHz
    double Q = 30.0;               // 品质因数

    // 初始化带阻滤波器
    Biquad filter;
    initBandStopFilter(&filter, fs, notchFreq, Q);

    // 示例输入信号（例如，1 kHz和5 kHz的正弦波叠加）
    int numSamples = 480; // 10ms的音频数据
    double inputSignal[480];
    double outputSignal[480];

    // 生成示例输入信号
    for(int i = 0; i < numSamples; i++) {
        double t = (double)i / fs;
        // 生成1 kHz的信号和5 kHz的信号
        inputSignal[i] = sin(2.0 * M_PI * 1000.0 * t) + 0.5 * sin(2.0 * M_PI * 5000.0 * t);
    }

    // 处理信号
    for(int i = 0; i < numSamples; i++) {
        outputSignal[i] = processSample(&filter, inputSignal[i]);
    }

    // 输出处理后的信号（这里只打印前10个样本作为示例）
    printf("Processed Output (first 10 samples):\n");
    for(int i = 0; i < 10; i++) {
        printf("%f\n", outputSignal[i]);
    }

    return 0;
}

代码说明

滤波器结构体（Biquad）：

  • b 0 , b 1 , b 2 b_0, b_1, b_2 b0,b1,b2：前向滤波器系数。

  • a 1 , a 2 a_1, a_2 a1,a2：反馈滤波器系数。

  • x 1 , x 2 x_1, x_2 x1,x2：前两个输入样本的状态变量。

  • y 1 , y 2 y_1, y_2 y1,y2：前两个输出样本的状态变量。

初始化函数（initBandStopFilter）：

实现带阻滤波器的参数初始化，包括预畸变计算、系数求解与归一化，以及状态变量初始化，确保滤波器按设计参数工作。

via:

相关推荐
茜茜西西CeCe3 个月前
数字图像处理-图像增强（2）
人工智能·算法·计算机视觉·matlab·数字图像处理·图像增强·陷波滤波器
热门推荐
01GitHub 镜像站点022025年大语言模型技术全景报告03Linux下V2Ray安装配置指南04安娜的档案(Anna’s Archive) 镜像网站/国内最新可访问入口（持续更新）05UV安装并设置国内源06Labelme从安装到标注：零基础完整指南07Claude Code Skills 实用使用手册08AI 规范驱动开发“三剑客”深度对比：Spec-Kit、Kiro 与 OpenSpec 实战指南09BongoCat - 跨平台键盘猫动画工具10在VSCode配置Java开发环境的保姆级教程（适配各类AI编程IDE）