Chapter 5 Basic Addition and Counting
5.1 Bit-Serial and Ripple-Carry Adders
单比特的半加器和全加器是通用的基本构件,用于合成加法器以及许多其他类型的算术电路。一个半加器接收两个输入比特x和y,产生一个和比特s=x⊕y=xy'+x'y和一个进位比特c=xy。图5.1描绘了半加器的多种可能逻辑实现中的三种。一个半加器可以看作一个单比特二进制加法器,它产生其单比特输入的2比特和,即x+y=(couts)two,其中该表达式中的加号代表算术和而非逻辑或。

一个单比特全加器定义如下:
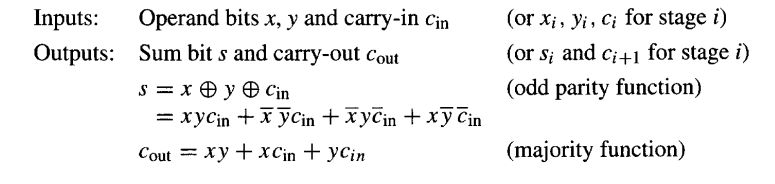
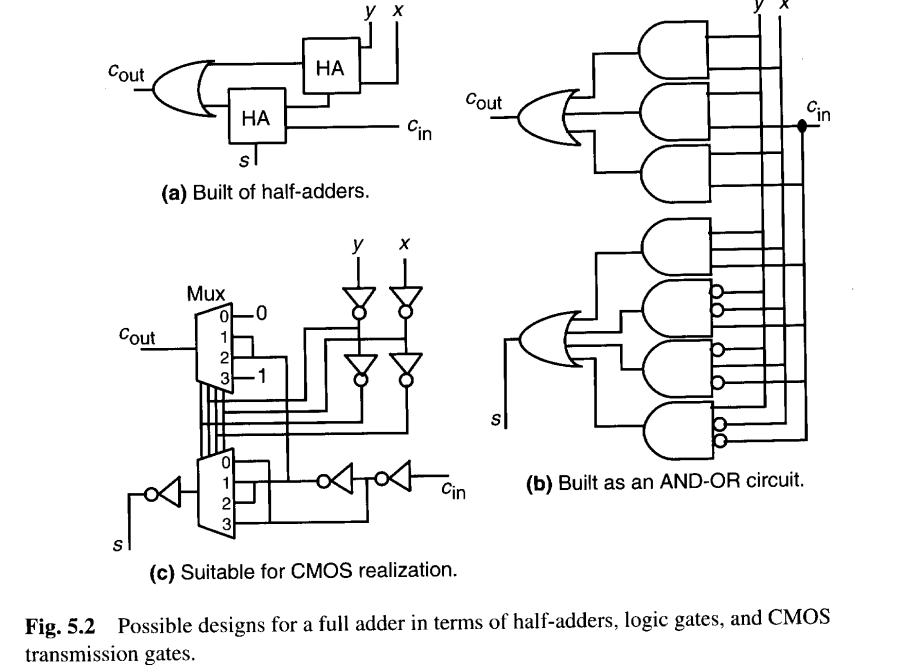
如图5.2a所示,一个全加器可以用两个半加器和一个或门来实现。如果两个HA是带有互补进位输出的与非门半加器,则图5.2a中的或门可以用一个与非门替代。或者,可以根据前述s和cout的逻辑方程,将全加器实现为两级与或/与非-与非电路(图5.2b)。由于全加器作为算术构建块的重要性,针对各种实现技术存在许多优化的FA设计。图5.2c显示了一个由七个反相器和两个4选1多路复用器构成的全加器,适用于CMOS传输门逻辑实现。
全加器和半加器可用于实现多种算术功能。我们将在本章和后续章节中看到许多例子。例如,一个比特串行加法器 可以由一个全加器和一个进位触发器构建,如图5.3a所示。操作数存储在一对移位寄存器中,从最低有效位开始,每个时钟周期向FA提供一位,而和被移入结果寄存器。因此,k比特数的加法可以在k个时钟周期内完成。一个k比特的行波进位加法器需要k个全加器,其中第i个FA的进位输出连接到第(i+1)个FA的进位输入。得到的k比特加法器产生一个k比特的和输出以及一个进位输出;或者,cout可被视为一个(k+1)比特和的最高有效位。图5.3b显示了一个用于4比特操作数的行波进位加法器,它产生一个4比特或5比特的和。
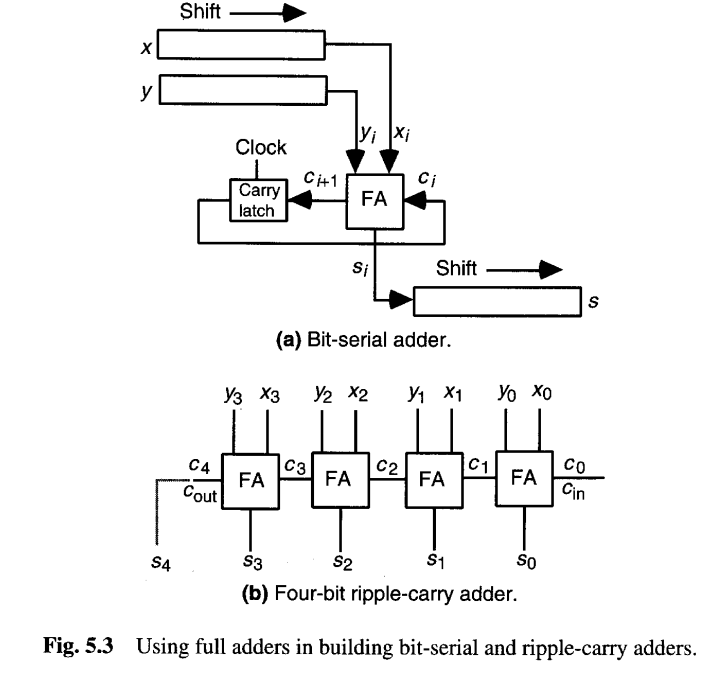
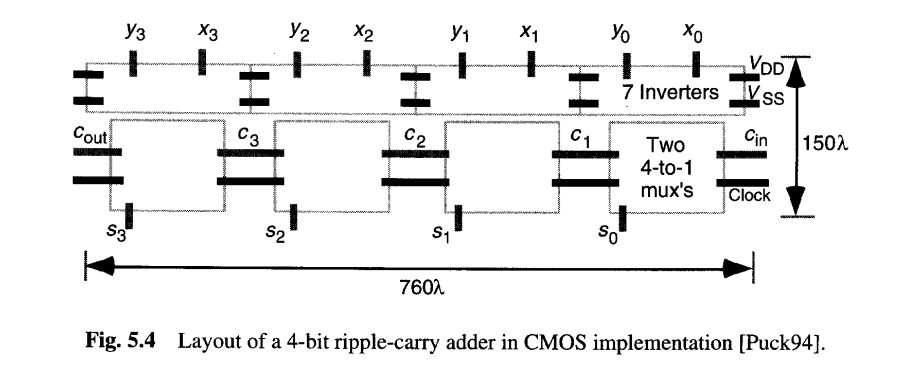
图5.3b所示的行波进位加法器直接导致了使用图5.2c全加器设计的CMOS传输门逻辑实现。图5.4描绘了一种可能的版图,该图还以λ(最小特征尺寸的一半)为单位显示了4bit行波进位加法器的大致面积需求。
k比特行波进位加法器的延迟 可以通过考虑最坏情况信号传播路径来推导。如图5.5所示,关键路径通常从x0 或y0输入开始,沿着进位传播链行进到最左边的FA,并在sk−1输出处结束。当然,对于某些FA实现,关键路径可能从c0开始和/或在ck结束。然而,考虑到从进位输入到进位输出的延迟比从x到进位输出或从进位输入到s的延迟更重要,全加器设计通常最小化从进位输入到进位输出的延迟,使得图5.5所示的路径成为具有最大延迟的路径。因此,我们可以为k 比特行波进位加法器的延迟写出以下表达式:
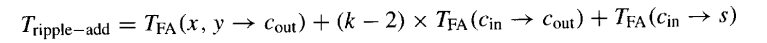
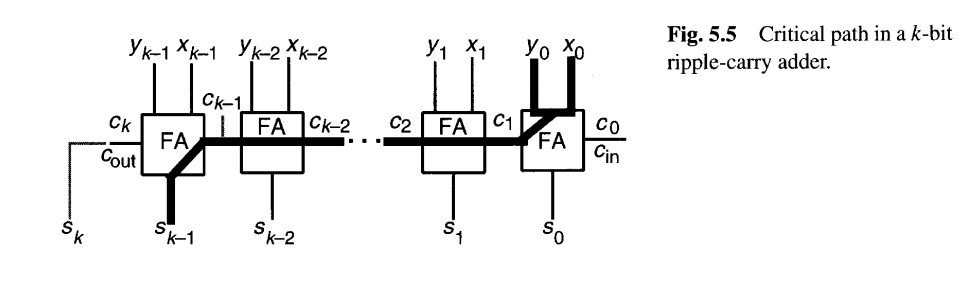
其中 TFA(input→output)TFA(input→output) 表示全加器在其指定输入和输出之间路径上的延迟。作为上述的近似,我们可以说行波进位加法器的延迟是kTFA。可以看到延迟随k线性增长,这使得行波进位设计对于高k或高性能算术单元来说是不可取的。请注意,比特串行加法器的延迟也是O(k),尽管由于锁存和时钟开销,这里的比例常数更大。
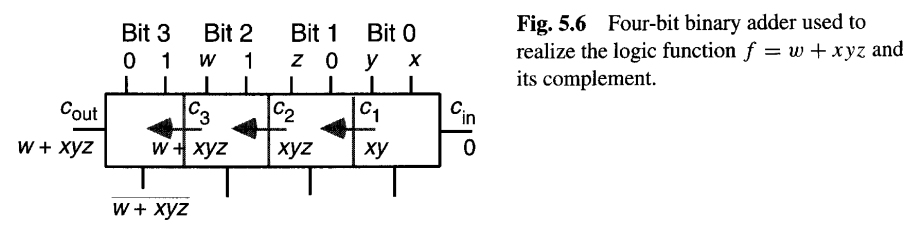
全加器和半加器以及多比特二进制加法器是强大的构建块,如果需要,也可用于实现非算术功能。例如,一个具有cin、两个4比特操作数输入、cout 和一个4比特和输出的4比特二进制加法器可用于合成四变量逻辑函数w+xyz及其补码,如图5.6所示。图5.6中写在箭头旁边的逻辑表达式表示各级之间的进位。但请注意,4比特加法器无需实现为行波进位加法器,输出端的结果仍然有效。
5.2 Conditions and Exceptions
当一个 k 位加法器用于ALU时,通常会提供**k** 位的和以及有关以下结果的信息,这些信息与条件/异常寄存器内的标志位相关联:

当我们进行无符号数 加法时,cout 和 "溢出" 是同一回事,而"符号"条件显然无关。对于二进制补码加法,当两个同符号数相加产生一个异符号的结果时,就会发生溢出。因此:

相当容易证明,二进制补码加法中的溢出可以从最左边的两个进位检测出来,如下所示:

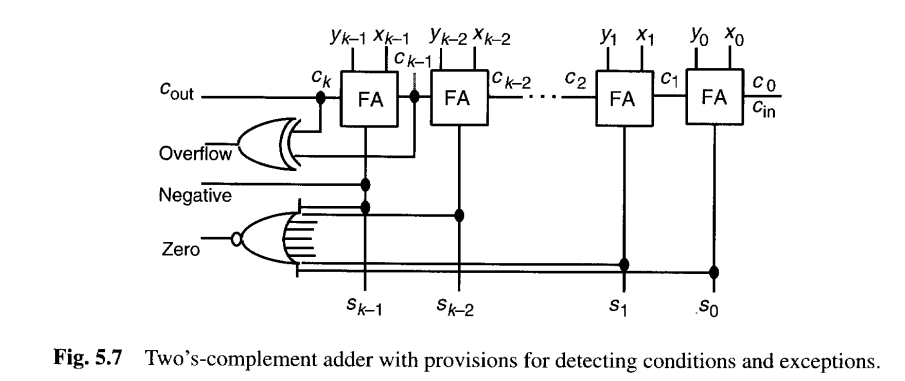
在二进制补码加法中,cout 没有(算术)意义。然而,由于一个加法器经常被用于同时处理无符号数和二进制补码数,因此**cout**仍然有用。图5.7显示了一个无符号或二进制补码加法器的行波进位实现,它带有用于条件和异常的辅助输出。由于测试"零"的或非门输入数量众多,它必须实现为一个或树后接一个反相器。
5.6 Manchester Carry Chains And Adders
在接下来的三章中,我们将研究加速两个操作数(第6、7章)和多个操作数(第8章)加法过程的方法。对于两个操作数,快速加法的关键在于一个低延迟的进位网络,因为一旦知道进入位置i的进位,和位si就可以通过模加法从操作数位xi、yi和输入的进位ci在常数时间内确定:
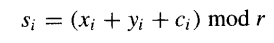
在基数为2的特殊情况下,上述关系简化为:
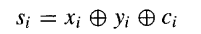
因此,设计两个操作数加法器的主要问题就是基于2k个操作数位xi和yi(0≤i<k)来计算k个进位ci+1。从进位传播和进位网络设计的角度来看,实际的操作数位并不重要。重要的是在给定位置,进位是被生成 、被传播 还是被消除。在二进制加法的情况下,生成、传播和消除信号由以下逻辑方程定义:

定义与以下事件对应的传递信号也很有帮助:给定进位输入为1,进位输出将为1:
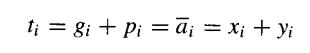
更一般地,对于基数r,我们有:
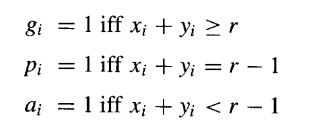
因此,假设上述信号被产生并可用,进位网络设计的其余部分可以基于它们,并且完全独立于操作数甚至数字表示的基数。使用前面的信号,进位递推关系可以写成如下形式:
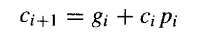
进位递推关系本质上表明,如果一个进位在i阶段被生成 ,或者它进入i阶段并被该阶段传播,那么它将进入阶段i+1。由于:
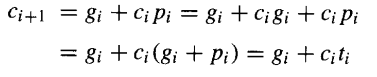
进位递推关系可以用ti代替pi来书写。后一个版本的进位递推关系会导致稍快一些的加法器,因为在二进制加法中,ti比pi更容易产生(或门代替异或门)。在下文中,我们始终以原始形式ci+1=gi+cipi 来处理进位递推关系,因为它更直观,但请记住,在大多数情况下,如果需要,pi可以被ti替换。
这个进位递推关系构成了一个称为曼彻斯特进位链的简单进位网络的基础。一个曼彻斯特加法器就是使用曼彻斯特进位链作为其进位网络的加法器。曼彻斯特进位链的每一级可以被视为由三个开关组成,这些开关由信号pi、gi 和 ai 控制,使得当相应的控制信号为1时,开关闭合(导通)。
如图5.13a所示,进位输出信号ci+1在ai=1时连接到0,在gi=1时连接到1,在pi=1时连接到ci,从而假定正确的逻辑值ci+1=gi+cipi。注意,信号pi、gi和ai中有且仅有一个为1。

图5.13b展示了如何在CMOS中实现曼彻斯特进位链。当时钟为低电平时,节点 c 预充电 。当时钟变为高电平时,如果gi为高电平,则ci+1'被拉低。为了防止gi影响ci,信号pi必须计算为xi和yi 的异或(而不是或)。这不是问题,因为无论如何我们都需要xi和yi的异或来计算和。
对于k位曼彻斯特进位链,总延迟由三个部分组成:
- 形成开关控制信号的时间。
- 开关的建立时间。
- 最坏情况下信号通过k个开关的传播延迟。
前两个延迟分量是小的常数项。因此,延迟主要由第三分量主导,该分量至少与k呈线性关系。对于现代CMOS技术,延迟大致与k^2成正比(因为k个传输晶体管串联连接),使得该方法不适合直接实现快速加法器。然而,当延迟实际上与k呈线性关系时,与基于门电路的行波进位加法器相比,速度有所提升,因为我们每级只有一个开关延迟,而不是两个门延迟。
曼彻斯特进位链的线性或超线性延迟限制了其在宽字长或高性能设计中的用处。它的主要应用是实现短链(例如,最多8位)作为构建块,与各种快速加法方案一起使用。
Chapter 6 Carry-LookAhead Adders
6.1 Unrolling The Carry Recurrence
回顾第5.6节中引入的辅助信号:gi(生成)、pi(传播)、ai(消除/吸收)和 ti(传递):
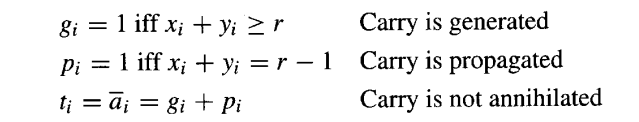
这些信号,连同进位递推关系:
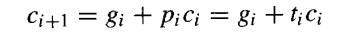
使我们能够将设计快速进位网络的问题与数字系统的细节(基数、数字集)分离开来。实际上,我们甚至不在乎做的是加法还是减法;只要我们简单地重新定义上述信号以对应借位的生成、传播等,任何进位网络都可以用作借位网络。
进位递推关系 ci+1=gi+pici表明,如果一个进位在第i阶段被生成 ,或者它进入第i阶段并被该阶段传播,那么它将进入第i+1阶段。人们可以轻松地展开这个递推关系,最终将每个进位ci表示为操作数位和cin的逻辑函数。以下是针对ci的三步展开过程:
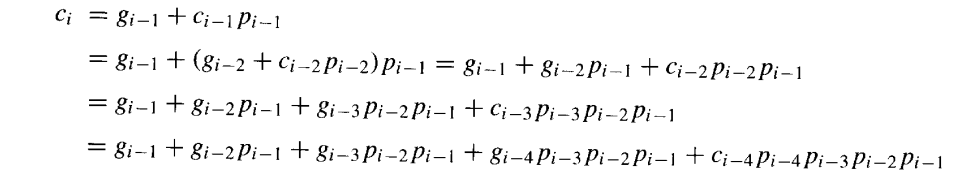
展开可以一直持续到最后一个乘积项包含c0=cin。展开后的进位递推关系有如下简单解释:当且仅当在第i−1 位生成一个进位 (gi−1),或者 在第i−2 位生成的进位被第i−1 位传播 (gi−2pi−1),或者在第i−3 位生成的进位依次被第i−2位和第i−1位传播 gi−3pi−2pi−1)等等,进位才会进入位置i。
在完全展开之后,我们可以直接利用辅助信号 (gi,pi) 和cin,使用最大扇入为k+1的两级"与-或"逻辑电路,来计算一个k位加法器中的所有进位。对于k=4,逻辑表达式如下:
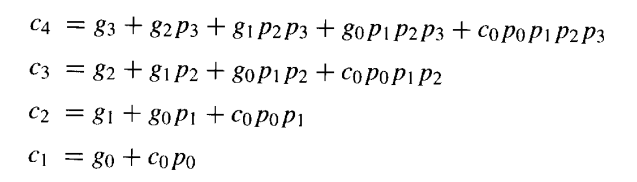
这里,c0和c4分别是4位加法器的cin和cout 。一个基于上述等式的进位网络,可以与产生gi 信号的2输入"与"门、以及产生pi信号和最终和位的2输入"异或"门结合,来构建一个4位二进制加法器。这样的加法器被称为具有完全超前进位。
请注意,由于c4不影响和位的计算,可以根据更简单的公式c4=g3+c3p3 来产生它,而几乎不会或完全不会造成速度损失。由此产生的进位网络如图6.1所示。
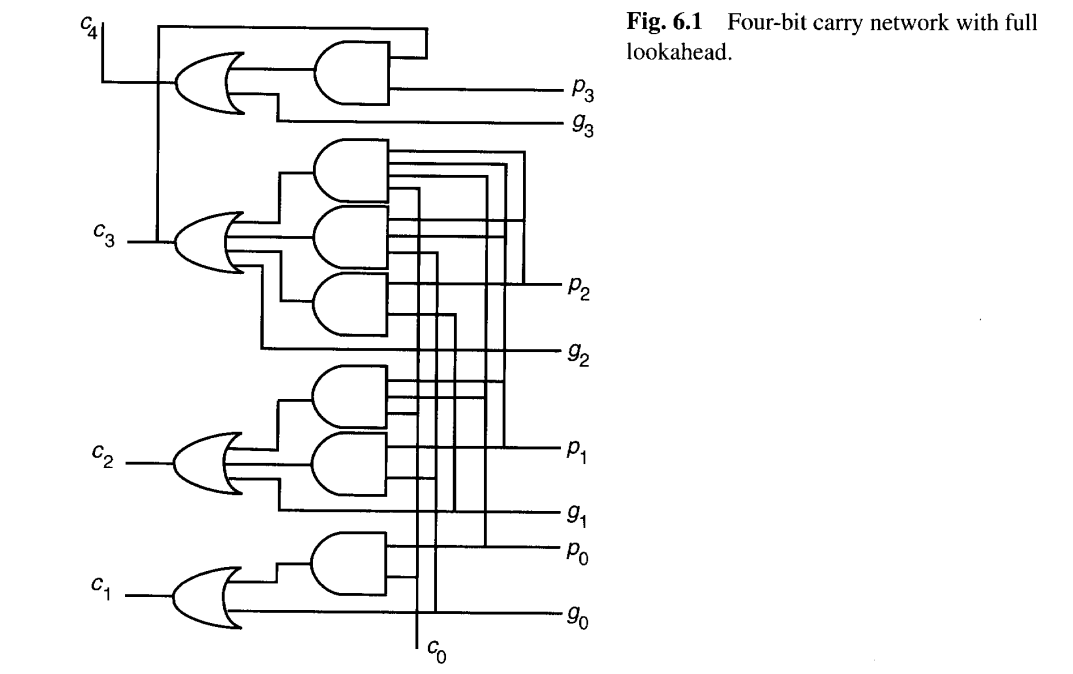
显然,对于宽字长来说,完全超前进位是不切实际的。例如,完全展开后的c31方程由32个乘积项组成,其中最大的项包含32个变量。因此,所需的"与"和"或"功能必须通过树状网络来实现,从而导致延迟和成本增加。有两种方案可以管理这种复杂性:
- 高基数加法(例如,基数为 2^8)
- 多级超前进位
高基数加法增加了生成辅助信号与和位数字的延迟,但简化了进位网络。根据实现方法和技术的不同,可能存在一个最优的基数。多级超前进位是实践中使用的技术,将在6.2节中介绍。
6.2 Carry-LookAhead Adder Design
考虑两个以 gi 和 pi 信号为特征的二进制数的基16加法。对于每个从原始二进制数的位 i 到位 i+3 的基16数字位置(其中 i 是4的倍数),可以推导出"块生成"和"块传播"信号如下:
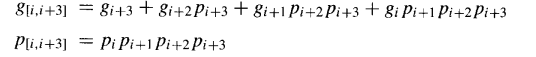
上述方程可以按照与展开进位方程相同的方式来解释:这四个比特位共同传播一个输入进位 ci,当且仅当这四个位置中的每一个都传播;它们共同生成一个进位,如果在位置 i+3 产生了一个进位,或者它在位置 i+2 产生并被位置 i+3 传播,等等。
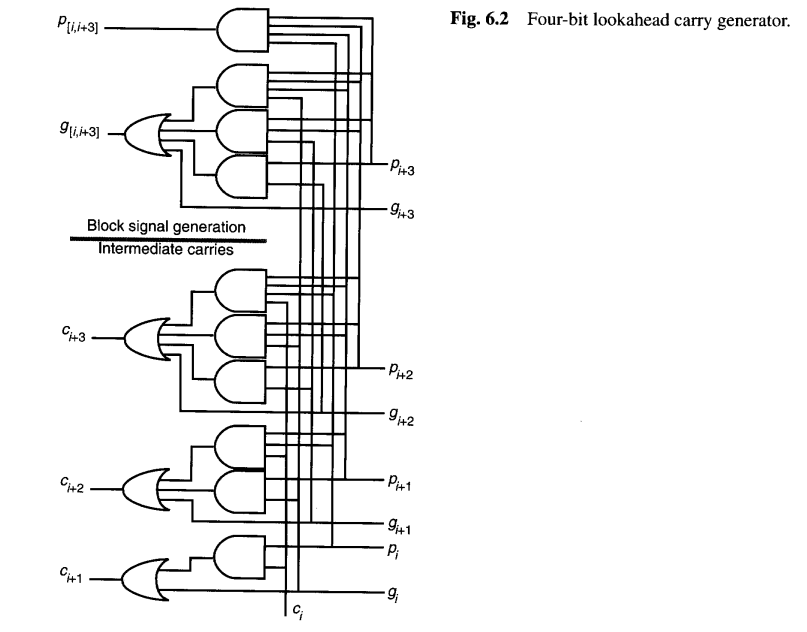
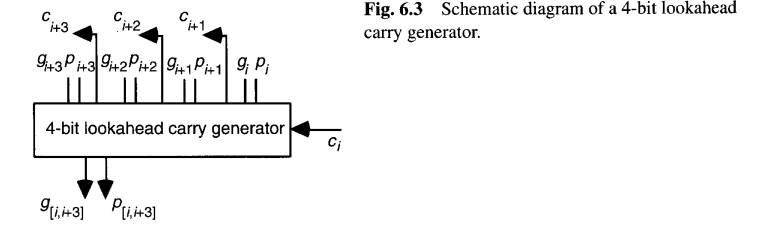
如果我们将图6.1进位网络中标有 c4 的部分替换为能产生块生成和块传播信号 g[i,i+3] 和 p[i,i+3] 的电路,就得到了图6.2的4位超前进位生成器。图6.3以示意图形式展示这个4位超前进位生成器。我们很快将看到,这样的模块可以在多级结构中用于构建任意所需宽度的进位网络。
首先,让我们对块生成和块传播信号采取一个更一般的视角。假设 i_0 < i_1 < i_2,我们可以写出:
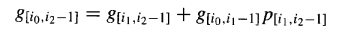
这个方程本质上表明,当且仅当在[i1, i2-1]块中生成了进位,或者 在[i0, i1-1]块中生成的进位被[i1,i2-1]块传播时,一个进位才会由从i0到i2-1的位置块生成。类似地:
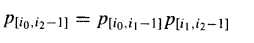
实际上,合并成更大块的两个块不必是连续的;它们也可以是重叠的 。换句话说,对于可能重叠的块 [i1,j1] 和 [i0,j0](满足i0≤i1-1≤j0<j1),我们有:
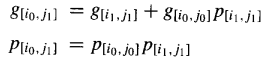
图6.4展示了如何用一个4位超前进位生成器将来自相邻或重叠块的 g 和 p 信号合并成组合块的 p 和 g 信号。

有了图6.3的4位超前进位生成器,基于多级超前进位方案来合成更宽的加法器就是一件容易的事了。例如,要构建一个两级的16位超前进位加法器,我们需要四个4位加法器和一个4位超前进位生成器,按照图6.5右上象限所示的方式连接在一起。在这种情况下,该4位超前进位生成器可以看作是在预测一个4位基16加法中的三个中间进位。通过这个16位加法器的延迟包括以下部分所需的时间:
-
产生单个比特位的**
g** 和**p**信号(1级门延迟)。 -
产生4位块的**
g** 和**p**信号(2级门延迟)。 -
预测各块的进位输入信号
c4、c8和c12(2级门延迟)。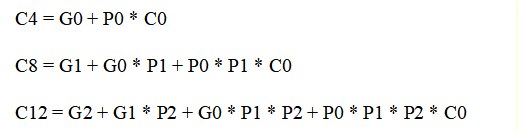
-
预测每个4位块内部的进位(2级门延迟)。
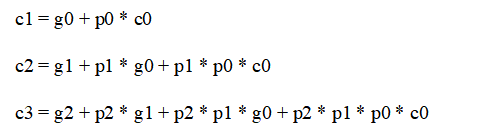
-
计算和位(2级门延迟)。(利用已经计算好的进位 ci 和每位的传播信号 pi(或原始输入 xi, yi),计算最终的和位 si=pi⊕ci=(pici') + (pi'ci))
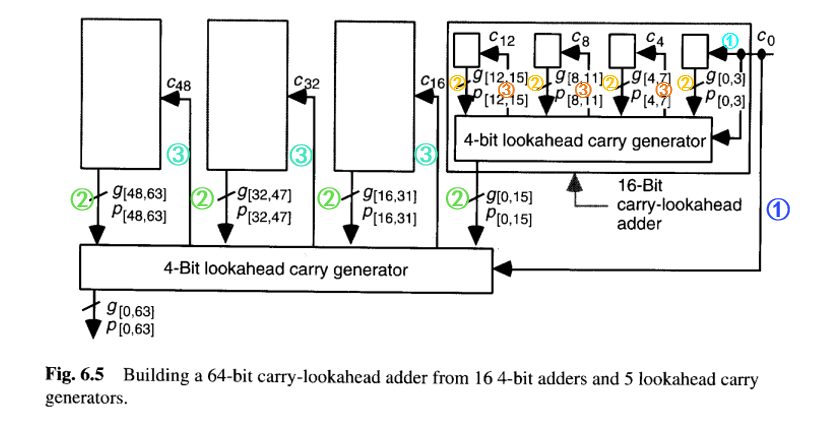
因此,16位加法器的总延迟为9个门级 ,这比16位行波进位加法器所需的32个门级要好得多。类似地,要构建一个三级的64位超前进位加法器,我们可以使用四个上述的16位加法器外加一个4位超前进位生成器,如图6.5所示连接。**每增加一级超前进位,延迟将增加四个门级:其中两个门级用于产生和传播信号(g和p)的向下传递(自下而上),另外两个门级用于进位通过额外层级向上传播(自顶向下)。**因此,基于4位超前进位模块的k位超前进位加法器的延迟为:
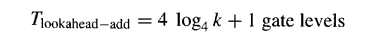
因此,图6.5中的64位超前进位加法器的延迟为13个门级。当然,也可以使用6位或8位的超前进位模块来减少给定字宽所需的超前进位级数。但考虑到更高扇入门带来的更长延迟,这样做可能并不值得。当字宽不是4的幂时,超前进位生成器的一些输入和/或输出将保持未使用状态,延迟公式变为4[log4k]+1。
关于图6.5所描绘的设计还有最后一点:这个64位加法器不产生进位输出信号(c₆₄),而许多应用都需要该信号。在超前进位加法器中有两种方法可以解决这个问题。一种是根据辅助信号或第k-1位的操作数和结果位在外部生成 c_out:
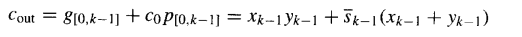
另一种方法是设计一个比所需宽1位的加法器(例如,需要60位时设计成61位),将额外的那一位和数用作cout。
Chapter 7 Variations in Fast Adders
7.3 Carry-Select Adders
最早的对数时间加法器 设计之一基于条件和加法算法 。在该方案中,比特块以两种方式进行加法运算:假设输入进位为0或为1,之后当该块的真实进位输入已知时,再选择正确的输出。随着每一级选择,已知的输出比特数量翻倍,从而选择级数呈对数关系**,实现对数时间的加法运算** 。条件和加法器的构建基础是进位选择原理,本节将对此进行描述。
一个(单级)进位选择加法器是将三个任意设计的 k/2 位加法器组合成一个 k 位加法器(图7.9)。一个 k/2 位加法器用于直接计算 k 位和的低半部分。另外两个 k/2 位加法器用于在两种不同场景下(c{k/2} = 0 或 c{k/2} = 1)计算和的高 k/2 位以及进位输出。当 c{k/2} 的值已知时,即可选择加法器进位输出信号以及位置 k/2 到 k-1 的和比特的正确值。最终得到的 k 位加法器的延迟,比构成它的 k/2 位加法器的延迟多出两个门级。
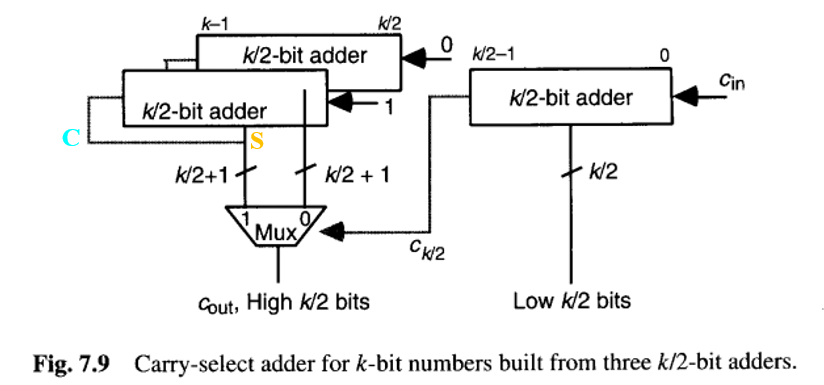
以下简单分析展示了进位选择方法的成本效益。让我们以单个比特的2选1多路复用器的成本和延迟为单位 ,并假设一个 k 位加法器的成本和延迟分别为 C{add}(k) 和 T{add}(k)。那么,图7.9的进位选择加法器的成本和延迟为:
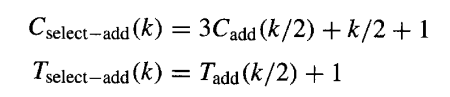
如果我们将成本与延迟的乘积作为成本效益的度量标准,那么当且仅当下式成立时,图7.9的进位选择方案比用于合成其组件加法器的方案更具成本效益:
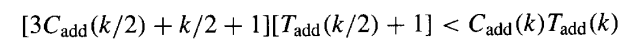
对于行波进位加法器,我们有 C{add}(k) = αk,T{add}(k) = τk。为简化分析,假设 τ = α/2 > 1。那么,很容易证明,当 k > 16/(α - 1) 时,进位选择方法比行波进位方案更具成本效益。例如,当 α = 4、τ = 2 时,进位选择方法几乎总是优于行波进位。可以进行类似的分析来比较进位选择方法与其他加法方案。
请注意,在前面的分析中,假设使用了三个完整的 k/2 位加法器。对于某些加法器类型,图7.9左侧的两个 k/2 位加法器可以共享部分硬件,从而获得更高的成本效益。例如,如果所用的组件加法器是超前进位类型,则计算 c{k/2} = 0 和 c{k/2} = 1 时和比特的两个加法器之间可以共享大部分进位网络。
请注意,当组件加法器的宽度不同时,进位选择方法同样有效。例如,图7.9可以用一个 a 位和两个 b 位加法器来构成一个 (a+b) 位加法器。此时,c_a 将通过一个 (b+1) 位的多路复用器来选择高 b 位的和。当选择信号 c_a 的推导延迟与和比特的延迟不同时,组件加法器采用不同的宽度是合适的。
图7.10描绘了如何将进位选择思想更进一步,以获得一个两级进位选择加法器 。对于每个 k/4 位块(最右边的块除外),都在两种场景下计算其和与进位输出比特。三个第一级多路复用器(每个宽度为 k/4 + 1 比特)将 k/4 位块的结果合并为 k/2 位块的结果。请注意,跨越比特位置 k/2 到 3k/4 - 1 的加法器的进位输出信号,是如何用于在 c{k/2} = 0 或 c{k/2} = 1 两种场景下选择和的最重要的 k/4 位比特的。在此阶段,最终和的 k/2 个比特是已知的。第二级多路复用器(宽度为 k/2 + 1 比特)用于为和的高 k/2 位(位置 k/2 到 k-1)以及加法器的进位输出选择合适的值。
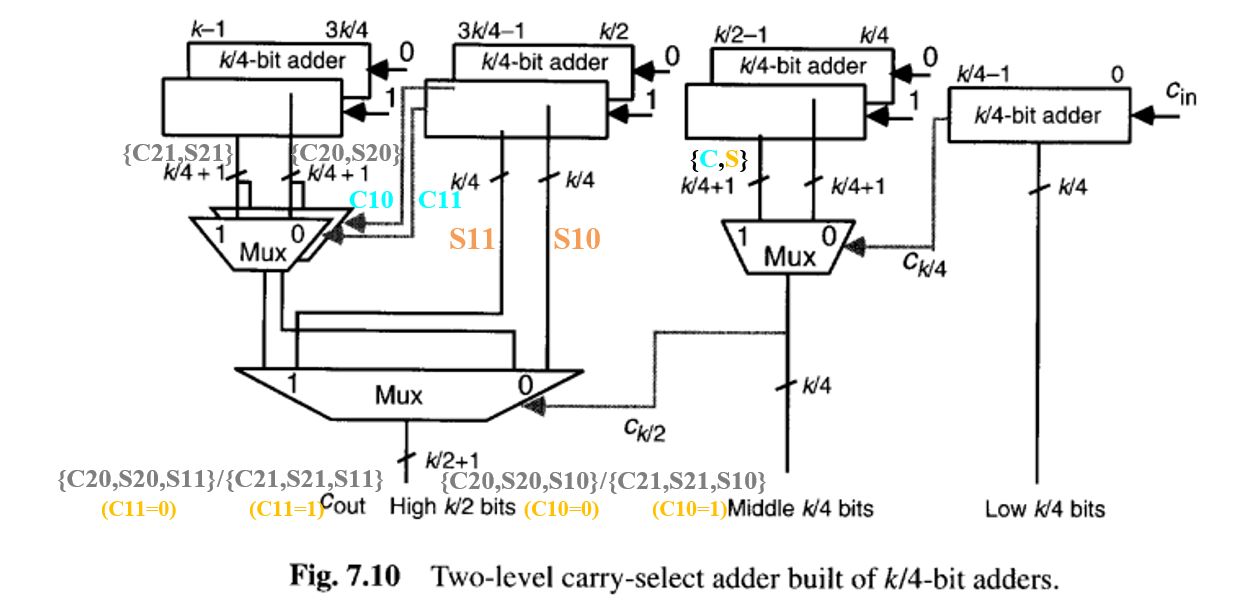
将图7.10的两级进位选择加法器与类似的两级超前加法器(图6.5,但使用2位而非4位的超前进位生成器)进行比较,我们注意到图7.10中单向的自顶向下数据流使得流水线化更容易、更高效。当然,从第6.5节和图6.13的例子中我们知道,进位超前进位加法器也可以实现为具有单向数据流。在这种情况下,比较就有些困难了,因为进位选择加法器的上层结构(小型加法器)更复杂,而下层结构(多路复用器)更简单。
对于给定的字宽,哪种设计胜出取决于实现技术、性能要求和其他设计约束。通常,最佳选择是进位选择和超前进位的混合组合(见第7.5节)。
7.5 Hybrid Adder Design
混合加法器通过结合两种或多种设计方法的元素获得,以实现更高的性能、更好的成本效益、更低的功耗等。由于任意两种或多种设计方法可以以多种方式组合,混合加法器的可能设计空间是巨大的。这为匹配给定的需求和约束提供了极大的灵活性,同时也使得设计者寻找最优设计的任务变得不平凡。在本节中,我们将回顾几种可能的混合加法器作为代表性例子。
图7.9和7.10中的一级和两级进位选择加法器本质上是混合加法器,因为顶层的k/2位或k/4位加法器可以是任何类型 。++实际上,进位选择方案的一个常见用途是构建那些宽度如果用某些纯设计实现会导致效率低下的快速加法器。例如,当使用4位超前进位模块时,16位和64位超前进位加法器都可以被相当高效地合成(图6.5)。而一个32位加法器则需要两级超前进位,因此并不比64位加法器更快。使用16位超前进位加法器,加上一个进位选择层级来使宽度加倍,则可能得到一个更快的32位加法器。最终得到的加法器具有混合的进位选择/超前进位设计。++
反向的组合(即混合超前进位/进位选择)也是可能的,并且实际上应用相当广泛。一个混合超前进位/进位选择加法器的例子如图7.12所示。图中成对显示的小型加法器模块可以基于曼彻斯特进位链,它们向超前进位生成器提供所需的g和p信号,并且在模块进位输入信号已知后,计算出最终的中间进位以及和位。
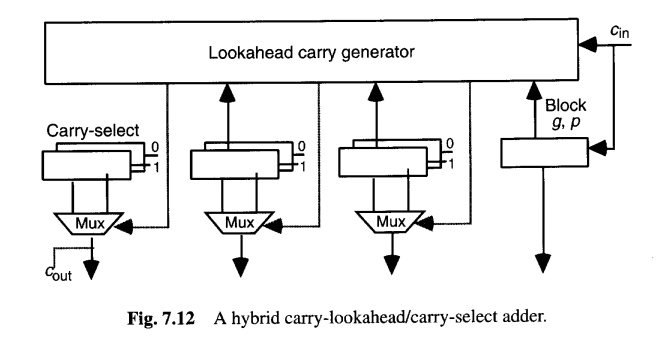
一个更宽的混合超前进位/进位选择加法器可能具有多级超前进位网络,而非如图7.12所描绘的单个超前进位生成器。如果所需的模块g和p信号能快速产生,超前进位网络中的信号传播可以与小型进位选择加法器中的进位传播完全重叠。图6.13中的超前进位网络实际上就是为这种混合方案而开发的,其中使用了基于曼彻斯特进位链的8位进位选择加法器 [Lync92]。这些8位加法器大约在与进位 c24,c32,c40,c48,c24,c32,c40,c48, 和c56可用的同一时间完成计算(图6.13)。因此,加法器的总延迟仅比超前进位网络的延迟多出两个逻辑级。
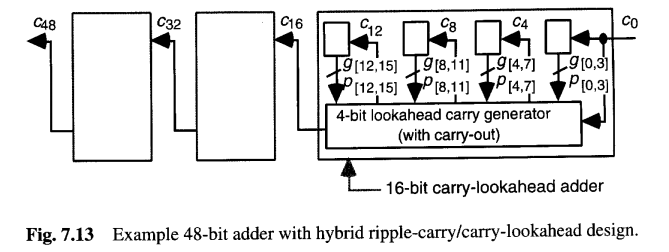
另一个有趣的混合设计是行波进位/超前进位加法器,其一个例子如图7.13所示。这种混合设计比纯超前进位方案稍慢,但其简单性和更高的模块化可能弥补这一缺点。这种混合设计相对于纯行波进位和超前进位加法器的成本和延迟分析留作练习,反向的超前进位/行波进位混合组合的开发和分析也同样留作练习。
我们最后一个混合加法器的例子使用了超前进位/条件和混合。条件和加法器对于宽字长的一个缺点是需要较低层级的多路复用器控制信号具有大的扇出(图7.10)。这个问题可以通过例如在较小的模块中使用条件和加法,并通过超前进位形成模块间进位来缓解。关于此类加法器(用于曼彻斯特大学MU5计算机)的详细描述,请参见 [Omon94, pp. 104-111]。
显然,可以以多种不同的方式组合来自各种设计的思想,从而催生出持续不断的快速加法器新实现和理论提案。考虑到特定技术的成本因素和基本约束 [Kant93],不同的组合会变得有吸引力。此外,应用需求(如低功耗)可能会改变平衡,使某种特定的混合设计更具优势。
7.6 Optimizations In Fast Adders
正如最优的进位跳跃加法器具有可变的块宽一样,通过优化块宽来减少其他(纯的或混合的)加法器的延迟也通常是可能的。例如,根据实现技术的不同,采用固定块的超前进位加法器可能无法达到最低可能的延迟[Niga95]。同样,确切的最优配置高度依赖于具体技术。事实上,在现代VLSI技术中,仅门数已不再是衡量实现成本的有意义指标。那些最小化或规整化互连的设计,尽管可能使用了更多的门,但实际上可能更具成本效益。对于特定混合设计或"最优"配置的成本效益的最终检验,是其在目标技术下实现时的实际速度与成本。
到目前为止,我们关于加法器延迟的讨论都基于一个默认的假设:所有输入数字一开始(或在时间0)就已全部就绪,并且所有输出数字都是在最坏情况的进位传播完成之后才被计算和取出的。另一种极端情况是,输入/输出数字串行到达和离开,这导致了非常简单的数字串行加法器设计。在这两种极端情况之间,存在着许多实际情况,其中输入数字的到达时间不同,或者某些输出数字必须比其他数字更早产生。
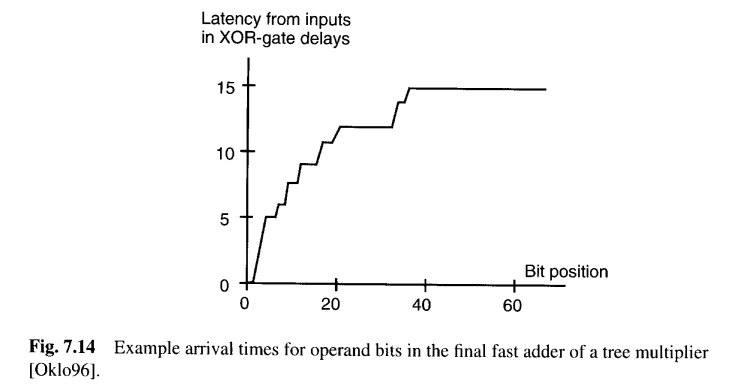
例如,我们稍后会看到,在将两个二进制数相乘时,部分积被归约为两个二进制数,然后这两个数在一个快速的双操作数加法器中相加以产生最终乘积。考虑到从原始输入到各个位的逻辑路径深度不同,这两个数的各个位会在不同时间就绪。图7.14显示了这种最终快速加法器的各个比特位上输入到达时间的一个典型例子。这些信息可以用于优化加法器的设计[Okl96]。
Chapter 8 Multioperand Addition
8.1 Using Two-Operand Adders
多操作数加法是乘法和向量内积计算中的基本操作(图 8.1)。在进行乘法运算时,被乘数a与k位乘数x相乘,需要生成k个部分积xia并相加。而在内积计算中,两个向量x和y对应元素相乘得到的分量乘积项 p(j)=x(j)y(j)也需要相加。计算平均值(例如均值滤波器设计)则是另一个需要多操作数加法的应用场景。

图 8.1 采用了"点表示法",这种方法在仅关注比特位置或对齐方式(而非具体数值)时非常有用。我们假设n个操作数均为宽度k的无符号整数,并按最低有效位对齐,如图 8.1 右侧所示。对有符号操作数的扩展方法将在 8.6 节讨论,而乘法应用则是第三部分的主题。
图 8.2 展示了使用单个双操作数加法器实现多操作数加法的串行解决方案。二进制操作数x(i)(i=0,1,...,n−1)每个时钟周期输入一个到加法器的某一端,另一端则接收来自部分和寄存器的反馈值。由于最终的和最大可达 n(2^k−1),部分和寄存器的宽度必须为log2(n2^k−n+1)≈k+log2n 位。
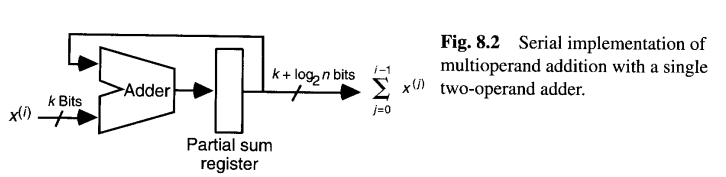
假设使用对数级延迟的快速加法器,图 8.2 方案对n个宽度为k的操作数求和的总延迟为:
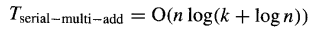
由于k+logn的值介于max(k,logn)和max(2k,2logn) 之间,可得log(k+logn)=O(logk+loglogn),因此:
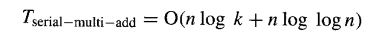
由此可见,当位宽k固定时,加法时间随操作数数量n超线性增长;而在给定n时,延迟随k对数增长。
我们可以对该串行方案进行流水化以提高性能。图8.3表明,若加法器采用四级流水线实现,则使用三个加法器即可达到每个时钟周期处理一个操作数的最大吞吐量。尽管流水线缩短了时钟周期,但对于任意固定的流水线级数h,从第一个输入到最后一个输出的延迟在渐进意义上保持不变。
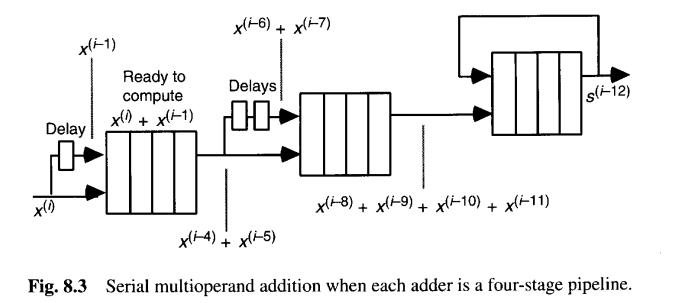
值得注意的是,只要将加法器替换为对应二元运算符⊗的硬件单元,图 8.2 和 8.3 的方案也适用于任何涉及二元运算符⊗的前缀计算。例如,类似设计可用于计算n个数的乘积或最大值。
为获得更高速度,可采用如图 8.4 所示的双操作数加法器树。这种二叉树结构需要n−1个加法器,若全部采用快速加法器,成本将相当高昂。
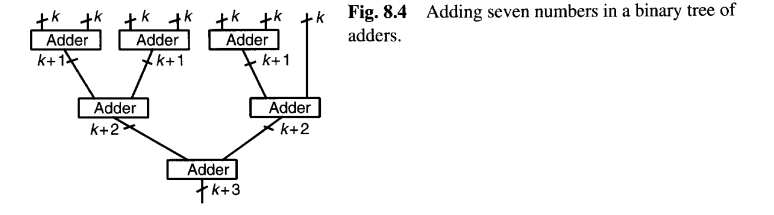
有趣的是,在这种设计中,使用简单且缓慢的纹波进位加法器(甚至位串行加法器)可能是最佳选择。若采用快速对数时间加法器,延迟为:
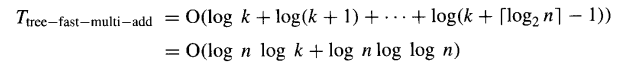
若在图 8.4 的树中使用纹波进位加法器,延迟变为:
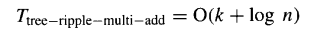
对于较大的n,该延迟可能小于使用快速加法器的延迟。
图 8.5 说明了纹波进位加法器树延迟为O(k+logn) 的原因:树中共有[log2n]层,第i+1层的加法器无需等待第i层完成全部进位传播,而可在第i层之后一个全加器延迟即开始计算。换言之,每一层的进位传播比前一层滞后一个时间单位。因此,除最后一层需要O(k+logn) 时间外,其余各层仅需常数时间。
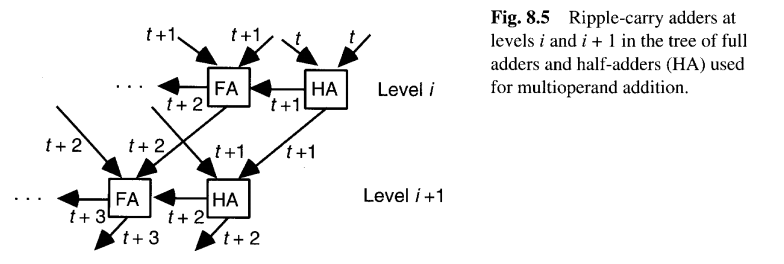
能否超越图 8.5 中纹波进位加法器树的O(k+logn) 延迟?理论最小延迟为 O(log(kn))=O(logk+logn),其中kn是多操作数加法器需处理的总比特数,而该加法器最终由恒定扇入的逻辑门构成。这一最小延迟可通过进位保留加法器实现。
8.2 Carry-Save Adders
我们可以将一排二进制全加器视为一种将三个数减少为两个数的机制,而非将两个数减少为它们的和的机制。图8.6展示了用于后一种减少的行波进位加法器与用于前一种减少的进位保留加法器之间的关系。如果进位被保存而不是传播,行波进位加法器就变成了进位保留加法器。
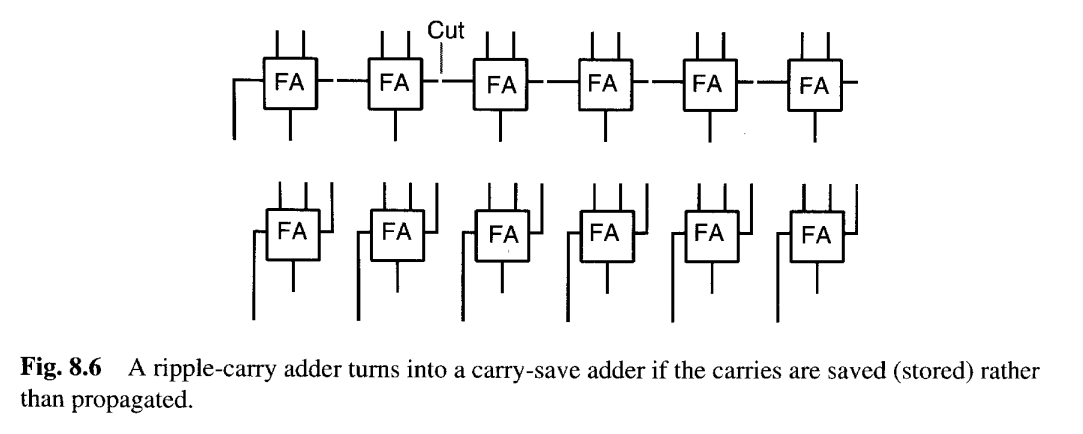
图8.7用点图表示了图8.6中所示的关系。为了更精确地说明各个点如何相关或获得,我们约定将构成全加器输入的任意三个点用虚线框围起来,并用对角线连接全加器的和输出与进位输出(图8.8)。偶尔,只有两个点被组合以形成一个和位和一个进位位。此时,将这两个点用虚线框围起来,并通过在对角线上加一条十字线来表示使用了半加器(图8.8)。
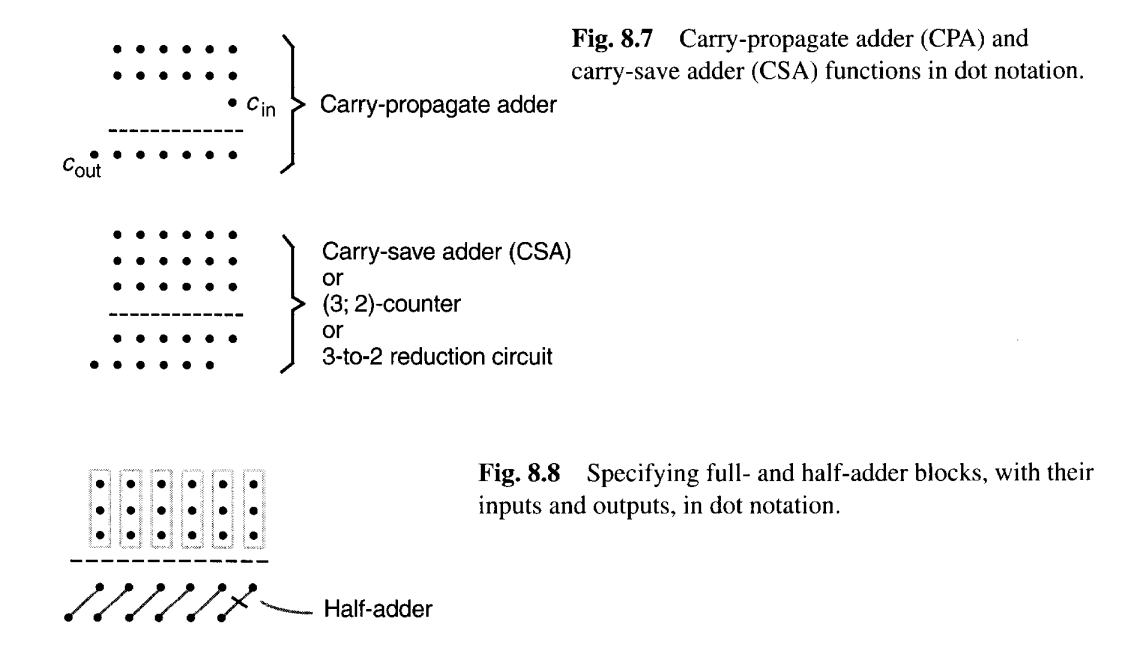
点图提出了另一种看待进位保留加法器功能的方式:用于将三个数 压缩为两个数(和向量与进位向量),而不进行进位传播。每个全加器独立计算本位和与向高位的进位,所有位的计算可以并行进行。
进位保留加法器树(图8.9)可以在**O(logn)层级(树高)**内将n个二进制数减少为两个具有相同和的数。

如果随后使用快速对数时间进位传播加法器来相加这两个结果数字,我们可以得到对于n操作数加法的成本和延迟如下:
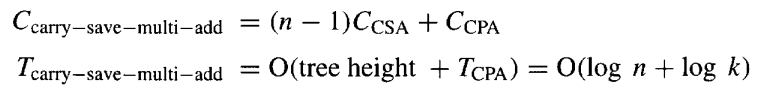
所需的进位保留加法器宽度各异,但通常宽度接近k位;进位传播加法器的宽度最多为 k+log2n。
图8.10展示了七个6位数相加的示例。图8.11描绘了同一过程的更紧凑表格表示,其中条目表示在相应列或位置上剩余的点数。我们从第一行开始,在位置0-5的每个位上都有七个点;这些点代表七个6位输入。在每列有7个点的列中使用两个全加器,每个全加器将其列中的3个点转换为该列中的一个点和下一更高列中的一个点。这导致了图8.11第二行所示的点分布。接下来,在包含3个或更多的点的每个位位置0-5中使用一个全加器,以此类推,直到没有一列包含超过2个点。此时,使用一个进位传播加法器将得到的两个数减少为最终的9位和,该和由位置0-8的每个位上的单个点表示。
在从前一行的条目导出一行的条目时,我们从第0列开始,逐步处理到最左边的列。在每一列中,我们取出3的倍数,并且对于取出的每一组三个点,我们在同一列中保留1个点,并在左边下一列中放入1个点。右侧已经减少到1的列不需要进一步减少。最右边含有2个点的列可以使用半加器进行减少,或者保持不变,将其减少推迟到最终的进位传播加法器。 前一种策略倾向于使最终进位传播加法器的宽度变小,而后一种策略则通过使用更宽的进位传播加法器来最小化全加器和半加器的数量。在图8.10的例子及其表格形式图8.11中,++我们本可以通过在位置1剩余的两个点上应用一个额外的半加器,将最终进位传播加法器的宽度从7位减少到6位。++

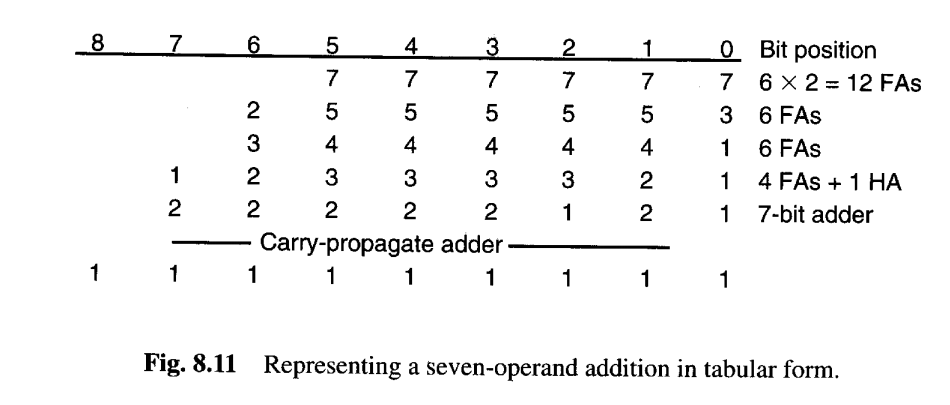
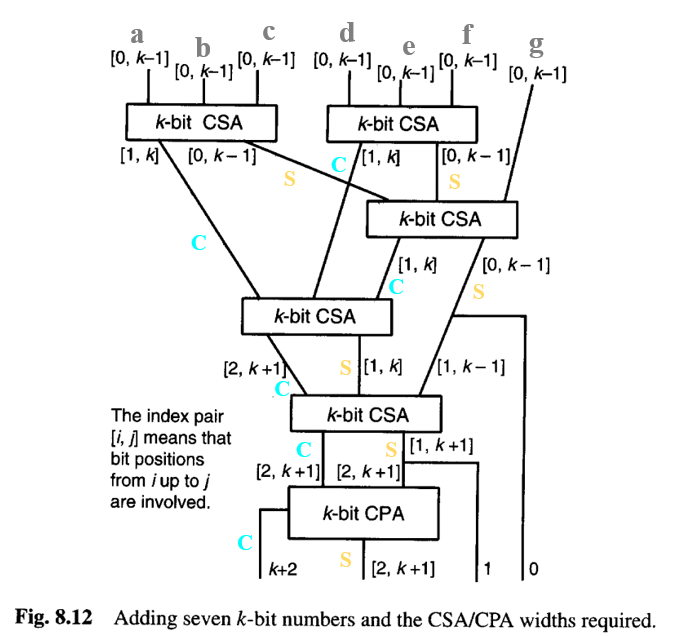
图8.12描绘了七个k位数进行进位保留加法的框图。通过在图中标记每条线所携带的比特位置,我们可以看到,++尽管随着更多数的合并,部分和的大小会增长,但进位保留加法器的宽度在整个树中基本保持不变++。注意,图8.12中最下面的进位保留加法器本可以只做成k−1位宽,方法是让位置1的两条线直接通过。这样,进位传播加法器就会变成k+1位宽。
当然,进位保留加法也可以使用单个进位保留加法器串行实现**(循环累加)** ,如图8.13所示。当操作数串行到达或必须从内存中逐个读出时,这是首选方法。但请注意,在这种情况下,进位保留加法器和最终的进位传播加法器都必须更宽(在串行累加过程中,部分和的位数会随着加法次数增加而扩展。n个k位数相加,最大可能和为:n*(2^k−1)≈n*2^k,该值需要k+[log2n] 位二进制数来表示。因此CSA的宽度 必须至少为k+[log2n]位,以避免中间结果溢出。CPA 的宽度同样需要扩展至此宽度,以正确处理最终的合并)。

8.3 Wallace And Dadda Trees
图8.12中的CSA树将七个k位操作数减少为两个具有相同和的(k+2)位操作数,被称为七输入华莱士树。更一般地,一个n输入华莱士树将其k位输入减少为两个(k + log₂n - 1)位输出。由于每个CSA将操作数数量减少到原来的1.5倍,n输入华莱士树的最小高度h(n)满足以下递归关系:
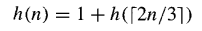
应用这个递归关系可以得到华莱士树高度的精确值。如果在前面的方程中忽略向上取整运算符,将其写作h(n) = 1 + h(2n/3),我们得到高度的下界:
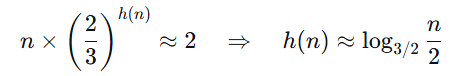
即h(n) ≥ log₁.₅(n/2),其中等号仅对n=2,3成立。另一种看待输入数量与树高度之间关系的方法是找出一个h层树能够减少到两个输出的最大输入数量n(h)。n(h)的递归关系为:

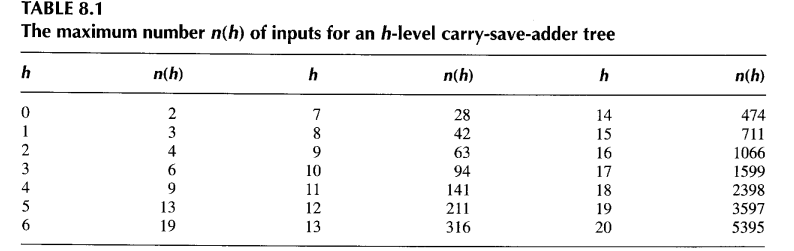
再次忽略向下取整运算符,我们得到上界n(h) ≤ 2(3/2)^h。下界n(h) > 2(3/2)^(h-1)也容易建立。表8.1给出了0 ≤ h ≤ 20时n(h)的精确值。
在华莱士树中,我们尽早减少操作数的数量 (见图8.10中的例子)。换句话说,如果一列中有m个点,我们立即对该列应用[m/3]个全加器。++这通过使最终的CPA位宽尽可能小,从而最小化总体延迟。++
然而,快速加法器的延迟通常不是字宽的光滑递增函数。例如,一个超前进位加法器对于17~32位的字宽可能具有基本相同的延迟。在Dadda树中,我们使用尽可能少的全加器和半加器将操作数数量减少到表8.1中下一个较低的n(h)值。 理由是,比如说7、8或9个操作数需要四个CSA级别,因此将操作数数量减少到表中下一个更低的n(h)值以下(如5)是没有意义的,因为这不会使树更快(树的层数已经确定)。++这种策略在保证性能的同时,减少了硬件成本(CSA数量)++。
让我们用Dadda的策略重做图8.10的例子。图8.14显示了结果。我们从七行点开始,所以我们的第一个任务是将行数减少到下一个较低的n(h)值(即6)。这可以通过使用6个全加器来完成;接下来,我们的目标是四行,导致使用11个全加器,以此类推。在这个特定的例子中,华莱士和达达方法导致了相同数量的全加器和半加器以及相同的CPA宽度。再次说明,通过在位置1使用一个额外的半加器,CPA宽度可以减小到6位。

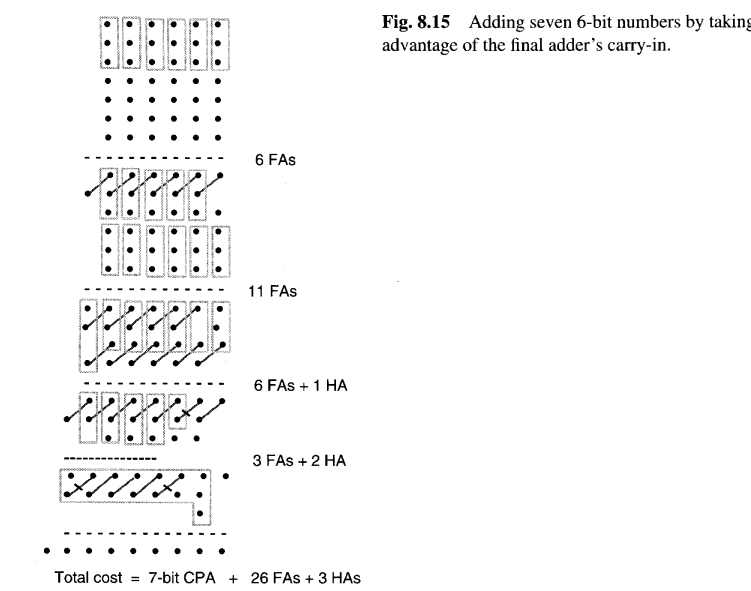
由于CPA有一个进位输入信号,可以用来容纳一个点,有时可以通过在加法器的最低有效位留下三个点来降低CSA树的复杂度。图8.15显示了与图8.10和8.14相同的例子,但用两个半加器替换了两个全加器,在位置1和2各留下一个额外的点。
8.4 Parallel Counters
一个单比特全加器有时被称为一个 (3; 2) 计数器 ,意思是它能统计其三个输入比特中"1"的个数,并将结果表示为一个2比特的数。这可以很容易地推广:一个(n; [log₂(n+1)])计数器有n个输入,并产生一个[log₂(n+1]比特的二进制输出,表示其n个输入中"1"的个数。这样的电路也被称为n 输入并行计数器。
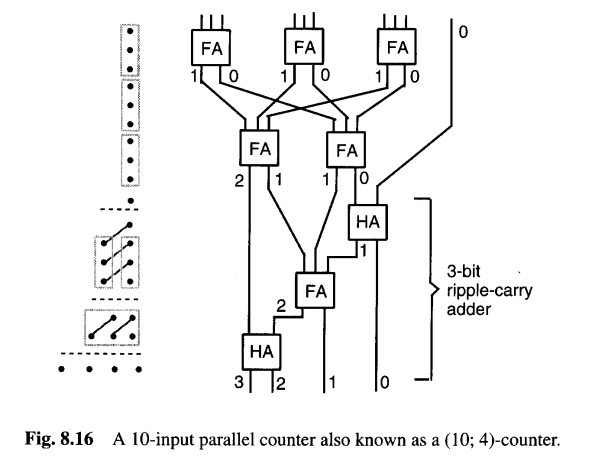
一个10输入并行计数器,或 (10; 4) 计数器,在图8.16中以点表示法和使用全加器、半加器的电路图两种形式描绘。一排这样的 (10; 4) 计数器(每个比特位一个)可以将一组10个二进制数减少为4个二进制数。这种规约的点表示法与 (3; 2) 计数器类似,只是连接 (10; 4) 计数器输出的每条对角线会穿过四个点。(7; 3) 计数器可以类似地设计。
尽管这种统计 n 个输入中"1"的数量的电路被称为并行计数器,但我们注意到这并不构成对顺序计数器概念的真正推广。一个顺序计数器接收单个比特(计数信号)并将其加到存储的计数值上。那么,一个并行计数器本可以定义为一种电路,它接收n个计数信号并将其加到存储的计数值上,从而实际上使计数值增加输入计数信号的总和。这种电路被称为"累加式并行计数器"。一个累加式并行计数器可以由一个并行增量器(一种接收一个数字并在输出端产生该输入数字与 n 个计数信号之和的组合电路)以及一个存储寄存器构成。无论是并行计数器还是累加式并行计数器,都可以通过考虑带符号的计数信号进行扩展。这将构成对顺序加/减计数器的推广。
8.5 Generalized Parallel Counters
一个并行计数器将同一比特位 上的多个点("点"代表一个值为0或1的比特)减少为分布在不同比特位 上的点(每位列一个)。这个思想可以很容易地推广到这样的电路:它接收一个"点阵"(不一定在一列中),并将其转换为另一个点阵(也不一定每列只有一个点)。如果输出点阵的总点数少于输入点阵,那么就发生了压缩;重复使用此类电路,最终可以将 n 个数减少为一小组数(理想情况下是两个)。
一个广义并行计数器由其每列输入的点数和每列输出的点数来表征。我们不会全面考虑这种电路,而是将讨论限制在那些每列只输出一个点的类型。因此,这类并行压缩器的输出侧同样可以用一个代表输出所跨越的列数的整数来表征。输入侧则由一系列整数来表征,这些整数对应不同列中的输入数量。
例如,一个 (4, 4; 4) 计数器接收两个相邻列中每列的4个比特(即四个2比特数),并产生一个4比特数来表示这四个2比特数之和。同样,图8.17描绘的 (5, 5; 4) 计数器将五个2比特数减少为一个4比特数。各列的输入点数不必相同。例如,一个 (4, 6; 4) 计数器接收6个权值为1的比特和4个权值为2的比特,并以一个4比特二进制数的形式输出它们的加权和。要使这种计数器可行,其输出位的总权重必须大于或等于其输入位的总权重。
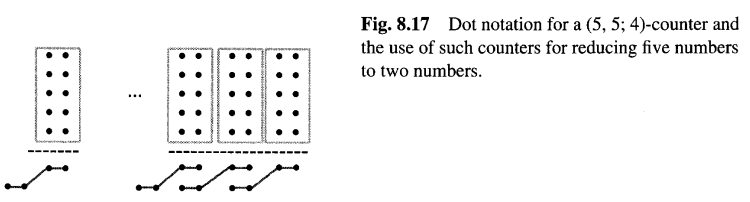
广义并行计数器非常强大。例如,一个4比特二进制全加器实际上就是一个 (2, 2, 2, 3; 5) 计数器。
由于我们在多操作数保留进位加法中的目标是将 n 个数减少为两个数,我们有时会谈论 (n; 2) 计数器 ,尽管根据我们之前的定义,对于 n > 3 的情况这并不成立。对于一个 n > 3 的(n; 2) 计数器,我们通常指的是一个电路切片,当它被适当地复制时,可以帮助我们将 n 个数减少为两个数。该电路的第 i 个切片接收位置 i 上的 n 个输入比特,加上来自一个或多个低位(i-1, i-2 等)的传送比特或"进位"比特,并在位置 i 和 i+1 产生输出比特,外加传送到一个或多个更高位(i+1, i+2 等)的传送比特。如果用 ψⱼ 表示从切片 i 传送到切片 i+j 的比特数,那么要使该方案可行,需满足的基本不等式为:
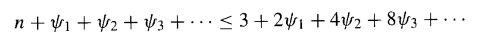
其中 3 代表两个输出比特(权值为 2⁰ 和 2¹)所能表示的最大值。例如,可以构建一个 (7; 2) 计数器,允许 ψ₁ = 1(即从位置 i 到位置 i+1 有 1 个传送比特),以及 ψ₂ = 1(即传送到位置 i+2 有 1 个比特)。为了获得最大速度,电路切片必须设计成使得传送信号尽可能靠近电路的输出端引入,以防止传送信号在多级中逐级传播。
8.6 Adding Multiple Signed Numbers
当要相加的操作数是二进制补码数时,如果多操作数加法要得出正确的和,就必须将它们符号扩展到最终结果的宽度。图8.18a 中的例子显示了符号位 x{k-1}, y{k-1}, z{k-1} 向左侧额外扩展了五个位置。

因此,当n很大时,符号扩展似乎会极大地增加用于n操作数加法的保留进位加法树(CSA Tree)的复杂度。然而,由于所有扩展的符号位是相同的,单个全加器就可以完成原本需要接收相同输入的多个全加器的工作。采用这种硬件共享方案,CSA 的宽度只会略微增加。对于图8.18a 中的三个操作数,可以用一个 (3; 2) 计数器(即一个全加器)来代替原本需要接收相同输入比特 x{k-1}, y{k-1}, z{k-1} 的六个 (3; 2) 计数器。
通过利用二进制补码表示中符号位的负权重解释,可以避免符号扩展 。一个负的符号位 -x{k-1} 可以被替换为 1 - x{k-1} = ¬x{k-1}(x{k-1} 的补码),并在同一列插入一个 -1 来抵消这个额外的 1。同一列中的多个 -1 可以配对,每对用一个高一位的 -1 代替。最后,如果某列剩下一个单独的 -1,则将其替换为该列的 1 和高一位的 -1。最终,所有的 -1 都会从最左端消失,最多只在某些列留下一个额外的 1。
图8.18b 展示了在三个二进制补码数相加时如何应用这种方法。三个符号位被取反,并在符号位位置插入了三个 -1。然后,这三个 -1 被替换为符号位的一个 1 和高一位(k)的两个 -1。接着,这两个 -1 被移除,取而代之的是在 k+1 位插入一个 -1。这个 -1 再被替换为 k+1 位的一个 1 和 k+2 位的一个 -1,依此类推。由于执行的是模 2^(k+5) 的 (k+5) 位二进制补码运算,从最左端移出的那个 -1 是无关紧要的。 (它用局部的、规则化的少量额外逻辑 (处理-1),换取了全局的、大面积的硬件节省(消除符号扩展),在高性能算术电路设计中是一个非常经典的优化。)
Chapter 9 BASIC MULTIPLICATION SCHEMS
将两个k位数相乘所需的乘法与加法运算,可通过k次移位加法循环来实现,该过程既可采用硬件固件实现,也可通过软件控制循环来完成。若存在一种专用指令,能够在乘法循环内完成部分或全部所需功能,那么情况会有所改善。

序列乘法可以通过保持累积部分积来实现。乘积 (初始化为 0) 并依次加上适当移位的项 xja。由于每个连续加入累积部分乘积的数都相对于前一个数移动一位,因此一种更简单的方法是将累积部分乘积移动一位,以使其位与下一个部分乘积的位对齐。这种算法可以设计两个版本,具体取决于图 9.1 中的部分乘积项 xja 是从高到低还是从低到高被处理。
在右移乘法中,部分积项xja从高到低累积:
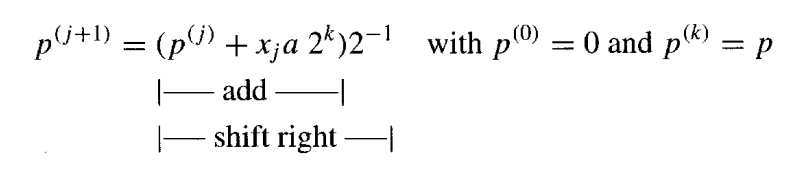
因为向右移动会导致第一个部分乘积在我们完成时被乘以 2^-k,所以我们将 a 预乘 2^k 以抵消向右移动的影响。这种预乘法是通过在加法步骤中将 a 与 2k 比特累积部分乘积的上半部分对齐来实现的 (即将 a 存储在double-length寄存器的左半部分)。

经过 k 次迭代后,结果如下:
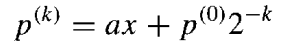
因此如果用y2^k代替P(0)则可以计算出ax+y的值。
在左移乘法中,部分积项xja从低到高累积:
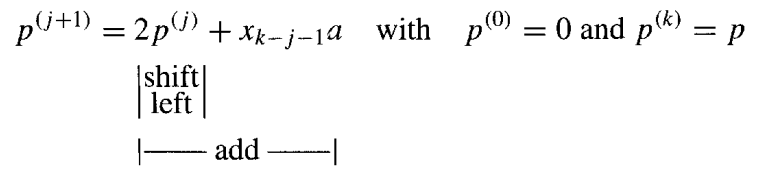
因为向左移动会导致第一个部分乘积在我们完成时被乘以 2^k,所以我们将 a 预乘 2^-k 以抵消向右移动的影响。这种预乘法是通过在加法步骤中将 a 与 2k 比特累积部分乘积的下半部分对齐来实现的 (即将 a 存储在double-length寄存器的右半部分)。

经过 k 次迭代后,结果如下:
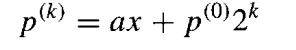
同理,用y2^-k代替P(0)可以计算出ax+y的值。
综上可以看出,这两种算法非常相似。它们都需要 k 比特的加法和 k 比特的移位。然而,左移算法中的加法宽度为2k比特 (由低k比特产生的进位可能会影响高k比特),而右移算法中的加法位宽为k比特。因此,使用右移进行乘法更为可取。
右移乘法算法的硬件实现如图 9.4 所示。乘数x和累积部分积p存储在移位寄存器中。待计算的乘数的下一位始终位于x寄存器的右端,用于选择0或被乘数进行加法。加法和移位可以在两个独立的周期或同一时钟周期内的两个子周期中进行。在任何一种情况下,都需要为加法器的进位信号提供临时存储。或者,移位可以通过将加法器的第i个和输出与部分乘积寄存器的第(k+i-1) 位相连,并将加法器进位放在第2k-1位,从而在同一周期内进行加法和移位。
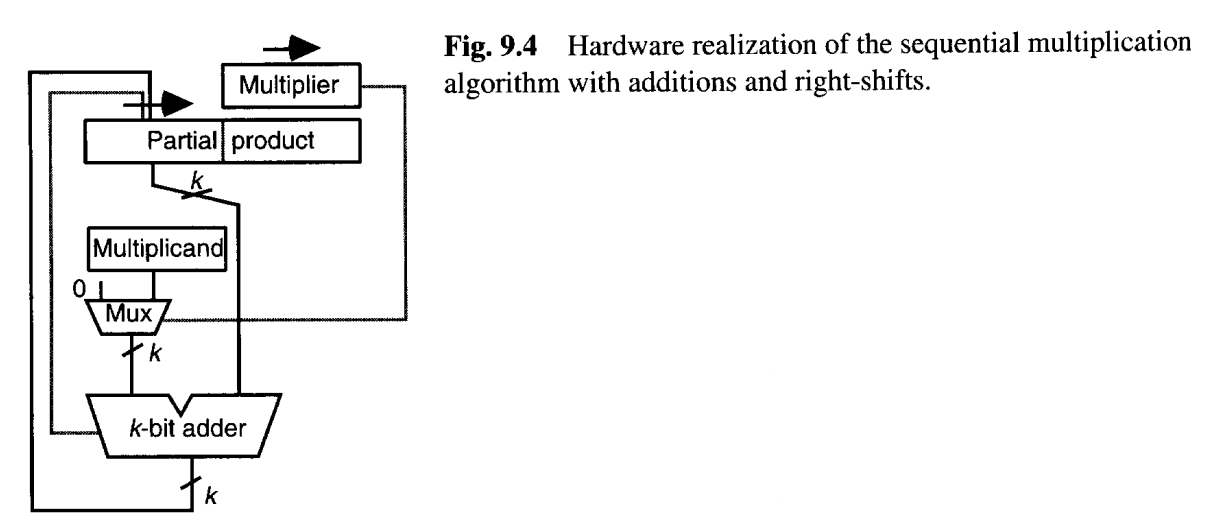
注意到**乘数x和部分积p的低半部分可以共享同一个物理寄存器。因为随着部分积p的数值向右扩展,而乘数x被使用过的位也被移出。**这样,只需要一个2k位的寄存器,就能同时存储迭代中的乘数和增长的部分积,节省了硬件资源。
图9.5展示了被累积部分积和乘数未使用的部分所共享的double-width寄存器,以及实现同时载入和移位所需的连接。由于寄存器在每个周期结束时载入累积部分积,因此控制当前mux的最低位的变化不会引起问题。
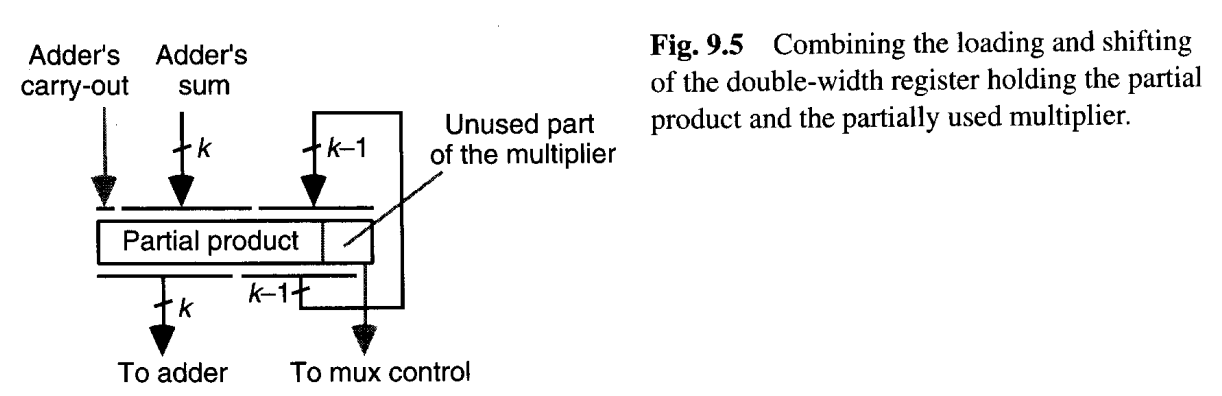
前面关于乘法算法和硬件实现的讨论假设了无符号操作数和结果。有符号数的乘法几乎不需要更多,因为乘积的符号可以通过 XOR 操作数的符号来单独计算。
使用补码表示法将有符号数相乘的一种方法是对负操作数 (s) 进行补码,将无符号值相乘,然后如果最初只有一个操作数进行补码,则对结果进行补码。这种间接乘法方案对于 1 的补码数来说相当高效,但对于 2 的补码表示法来说开销太大。对于这种数,最好使用直接乘法算法,本节余下部分将进行讨论。
我们首先注意到,前面的序列算法可以直接使用负的2's 补码被乘数和正的乘数。在这种情况下,每个 xja 项都将是一个 2's 补数,如果我们在加法过程中使用符号扩展值,则和将正确累加。图 9.7 显示了使用右移算法将负被乘数 a = (-10) = (10110) 2's-compl 乘以正乘数 x = (11) = (01011) 2's-compl。注意,和 p (i) + xia 的MSB是假设符号扩展的操作数。
鉴于2的补码数中符号位的负权重解释,如果最后一个周期中不是加上 x(k−1)a,而是减去它,则可以正确处理负的2的补码乘数。实际上,所需的减法通过加上被乘数的2的补码,或者实际上加上被乘数的1的补码并向加法器插入进位输入1来执行。所需的控制逻辑仅变得稍微复杂一些。图9.8显示了通过右移算法将负值 a=(−10)=(10110)2's-compl 和 x=(−11)=(10101)2's-compl 相乘。

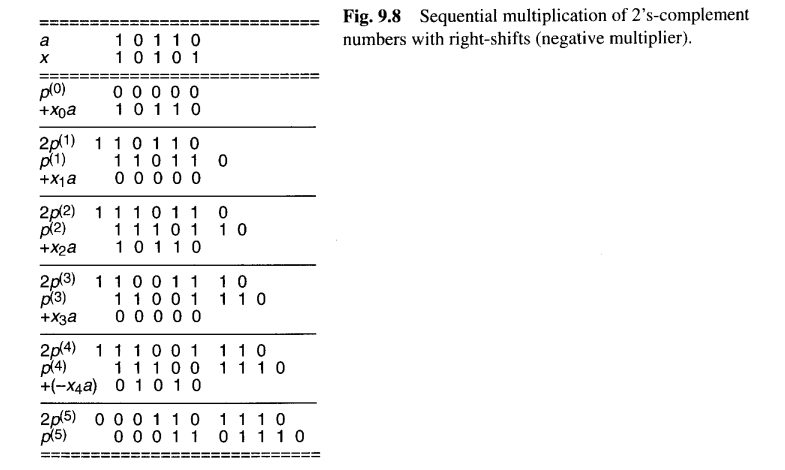
处理2的补码数的另一种方法是使用布斯重编码,将乘数x表示为有符号数字格式。
布斯重编码(也称布斯编码)最早是为了加速早期数字计算机中的基2乘法而提出的。回想一下,基2乘法由一系列移位和加法组成。当在某一步中向累积的部分积加上0时,加法操作可以完全跳过。这在图9.4和9.6的设计中没有意义,因为数据路径必须通过加法器。但在异步实现中,或在开发乘法程序时,仅移位比先加后移更快,人们可以利用这一事实来平均减少乘法时间。由此产生的算法或其相关的硬件实现将具有可变的延迟,这取决于乘数值:乘数x的二进制表示中1越多,乘法就越慢。
布斯观察到,每当在x中有大量连续的1时,可以通过将这串连续的加法替换为一次在最低有效端的减法和一次在最高有效端紧邻左侧位置的加法来加速乘法。即:
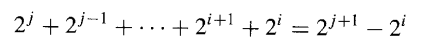
连续1的序列越长,实现的节省就越大。这种转换的效果是,将数字集为 [0, 1] 的二进制数x,转换为使用数字集 [−1, 1]的二进制有符号数字y。因此,布斯重编码可以看作是一种数字集转换。表9.1展示了如何从 x 的两个数字位 xi和 xi−1得到重编码数 y的数字位 yi。这样,当从右向左扫描x时,可以动态确定数字位 yi,并在每个周期中用来选择加、减或无操作。

例如,考虑以下16位二进制数及其重编码版本:

在这个特定例子中,重编码并没有减少加法的次数。然而,这个例子用来说明两点。第一 ,如果要保持x作为无符号数的值,重编码后的数字可能必须扩展一位。第二,如果x是一个2的补码数,那么不扩展长度(忽略上面重编码版本中最左边的1)可以正确处理负数。请注意在这个例子中,2的补码数的符号位在重编码版本中如何正确地承担了负权重。图9.9给出了一个完整的乘法示例。

Chapter 10 HIGH-RADIX MULTIPLIERS
10.1 Radix-4 Multiplication
本章将介绍在每个周期中处理超过一比特乘法器的乘法方案 (基4每个周期2bit,基8每个周期3bit,等等)。通过减少循环次数,以及使用重编码和进位保存加法来简化每个循环中所需的计算,可使速度比第 9 章中的基本乘法器有显著提高。
对于给定的数字表示范围,使用更高的表示基数会导致更少的数字位数。因此,当我们转向更高的基数时,一种序列乘法算法需要更少的周期。这激励我们研究高基数乘法算法及相关的硬件实现。由于一个k位二进制数可以解释为一个[k/2]位的基4数、一个[k/3]位的基8数,以此类推,因此使用高基数乘法本质上意味着在每个周期内处理乘数的多个比特位。
我们首先给出9.1节中乘法递推关系的通用基r版本:
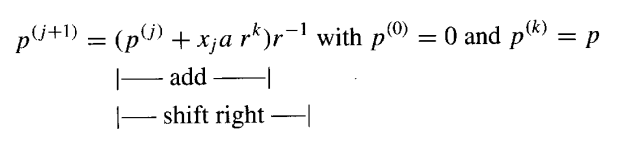

由于乘以 r^−1 或 r仍然意味着右移或左移一个数字位,高基数乘法与基2乘法的唯一区别在于形成项 Xia,而这现在需要更多的计算。
例如,如果以基数4进行乘法,在每一步中,都需要形成部分积项 (xi+1xi)twoa 并将其加到累积的部分积中。图10.1用点图表示了该乘法过程。直接应用这种方法会导致以下问题:在基2乘法中,部分积矩阵中的每一行点图代表0或a的移位版本,而这里我们需要倍数 0a、1a、2a和 3a。前三个没有问题,但计算 3a至少需要一次加法操作(3a=2a+a)。
在本节的剩余部分以及第10.2节中,我们将回顾针对基4乘法中前述问题的几种解决方案。
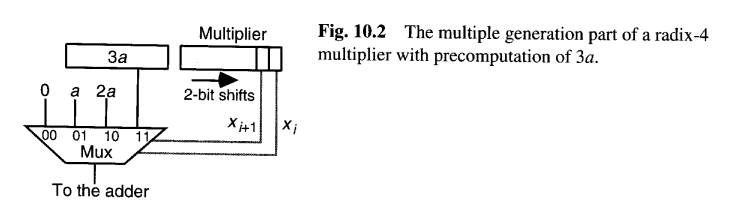
第一种 选择是在开始时计算一次3a并将其存储在寄存器中供将来使用**(预计算)**。然后,乘法器硬件的其余部分将与图9.4中描述的非常相似,只是两路复用器被替换为如图10.2所示的四路复用器。图10.3给出了一个乘法示例。
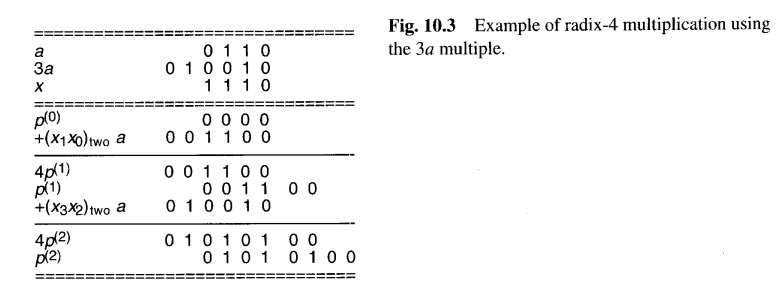
另一种 可能的解决方案是:++当需要加3a时,我们加−a并向乘数的下一个基4数字发送一个进位1++,如图10.4。考虑到输入的进位,每个周期所需的倍数在 [0, 4] 范围内。倍数0,1和2直接处理,而倍数3和4分别转换为−1和0,外加一个输出的进位1。由于进位,最后可能需要一个额外的周期。
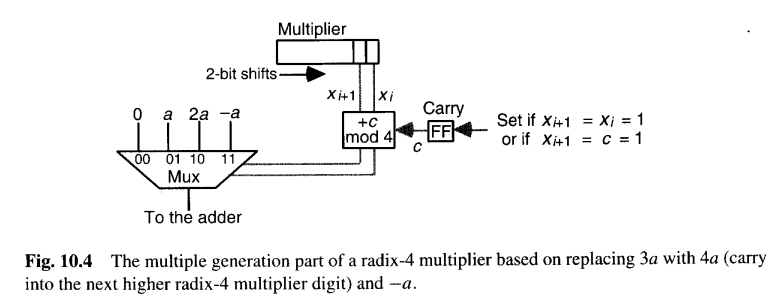
图10.2和10.4描绘的乘法方案可以扩展到基数8、16等,但对于更高的基数,倍数生成硬件会变得更复杂,从而抵消了由于周期减少所带来的大部分速度增益。例如,在基数8中,需要预先计算倍数3a、5a和7a,或者仅预先计算3a并使用进位方案类似于图10.4,将倍数5a、6a和7a分别转换为-3a、-2a和-a,并加上一个进位1。
10.2 Modified Booth's Recoding
如第9.4节末尾所述,基2布斯重编码并未直接应用于现代运算电路,但它可以作为理解更高基数版本布斯重编码的工具。不难看出,当使用表9.1对一个二进制数进行重编码时,结果中将不会出现连续的1或 -1。因此,如果使用重编码后的乘数执行基数4乘法,则仅需要被乘数的倍数 ±a和 ±2a,所有这些倍数都可以通过移位和/或取补轻松获得。
现在,由于yi+1依赖于xi+1和xi,而yi依赖于xi和xi−1,所以基数4数字zi/2=(yi+1yi)two(其中i 为偶数)可以直接从xi+1,xi 和xi−1获得,而无需先形成基数2的重编码数y(见表10.1)。
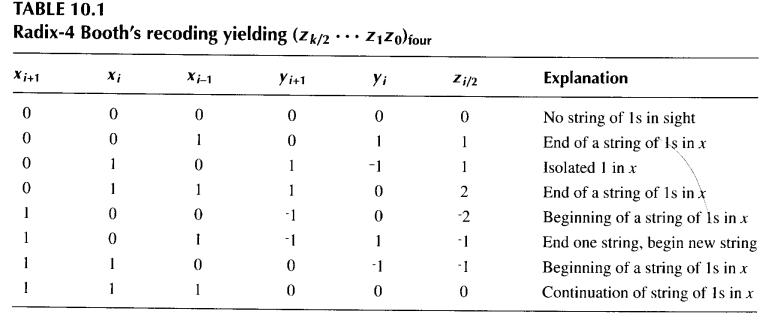
与基2版本类似,基数4布斯重编码可以被视为一种数字集转换:该重编码将一个数字在[0, 3] 范围内的基数4数字,转换为数字集为[-2,2]的数字。
例如,表10.1可用于将以下无符号数转换为有符号数字数:
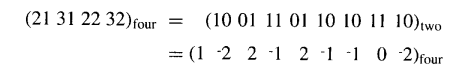
注意,这个16位无符号数变成了一个9位的基数4数。一般而言,对于一个k位无符号二进制数,当它的最高位为1时,其基数4有符号数字表示将需要 [k/2]+1=[(k+1)/2]个数字。还需注意,这里假设了 x-1=xk=xk+1=0。
如果前面例子中的二进制数被解释为2的补码格式,那么简单地忽略产生的额外基数4数字即可得到所表示值的正确编码:
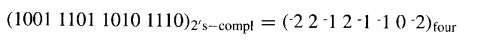
因此,对于k位2的补码格式的二进制数,布斯编码的基数4版本将有[k/2]个数字。当k为奇数时,为了正确重编码,假设 xk=xk-1。在任何情况下,x-1=0。
由基数4布斯重编码定义的数字集转换过程不涉及进位传播。每个在 [−2,2]范围内的基数4数字都是通过检查乘数的3个比特位独立获得的,且连续的3比特段之间有一个比特的重叠。因此,基数4布斯重编码被称为基于乘数的重叠3比特扫描。这可以扩展到更高基数的重叠多比特扫描方案(见第10.4节)。
图10.5展示了一个使用布斯重编码的基数4乘法示例。4位2的补码乘数x=(1010)被重编码为一个2位基4数z=(-1 -2)four,然后指定了在两个周期内要加到累积部分积上的倍数z0a=−2a 和 z1a=−a。注意,在所有中间步骤中,累积部分积的上半部分从4位扩展到了6位,以适应正确处理负值所需的符号扩展。同时,注意在右移过程中为从4p(1)得到p(1)而进行的符号扩展。
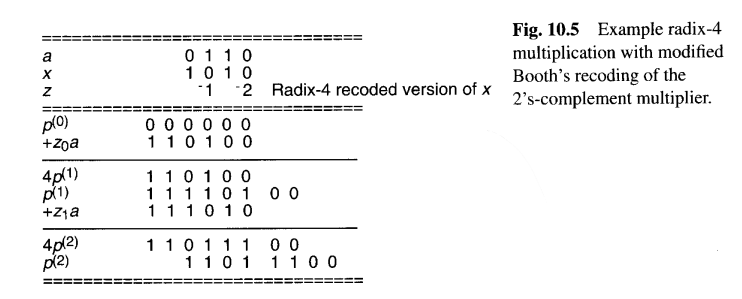
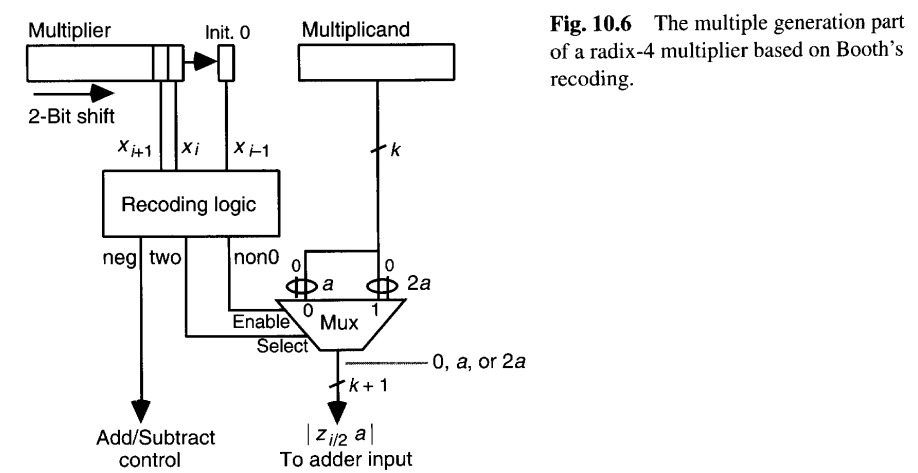
图10.6描绘了一个基于基数4布斯重编码的倍数生成电路的可能实现。由于涉及a的五个可能倍数或数字(0,±1,±2),我们至少需要3位来编码一个所需的倍数。一种简单高效的编码方式是:用一位来区分数字是0还是非零,一位来表示非零数字的符号,一位来表示非零数字的幅值(2编码为1,1编码为0)。因此,该重编码电路有三个输入(xi+1,xi,xi-1)并产生三个输出:"neg"指示倍数应被加上(0)还是减去(1),"non0"指示倍数是否非零,"two"指示一个非零倍数是2。
将图10.4设计中隐含的重编码方案与图10.6的布斯重编码在成本和延迟方面进行比较是很有启发性的。特别要注意的是,虽然图10.4中产生的重编码是串行的,因此必须从右向左进行,但布斯重编码是完全并行且无进位的。后一特性在设计逐数字乘法器时并无助益,因为重编码后的数字无论如何都是串行使用的。但我们稍后会看到,布斯重编码可以应用于树形和阵列乘法器的设计,其中所有倍数都需要同时生成。
10.3 Using Carry-Save Adders
进位保留加法器(CSA)既能用于减少加法周期数,也能使每个周期更快。例如,不使用布斯重编码的基4乘法可以通过使用CSA来处理倍数3a来实现,如图10.7
所示。这里,CSA帮助我们在不减少加法时间的情况下进行基4乘法(生成所需的倍数)。实际上,可以说加法时间略有增加,因为无论我们是否实际需要3a,每个周期都要承担CSA的开销。
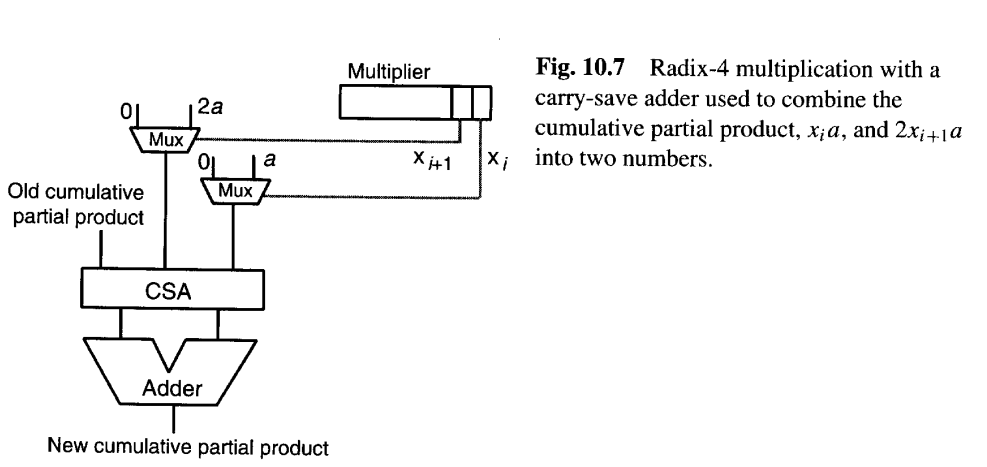
图10.7的基4乘法器中的CSA和多路复用器**可以通过将累积部分积保持在进位保存形式中(将部分积的高半部分用两个寄存器表示:和向量Sum和进位向量Carry),从而更好地减少基2乘法的加法时间。**实际上,只有累积部分积的上半部分需要以冗余形式保持,因为当我们将形成下一个累积部分积的三个值相加时,最终乘积的一个比特会以标准二进制形式获得,并被移入双宽度部分积寄存器的下半部分(图10.8)。这消除了除最终加法外所有进位传播的需要。
(在每次迭代中,CSA 计算后,我们可以立即将 CSA 输出的Sum和Carry的最低位合并得到一个确定的乘积位,并将其右移到低半部分寄存器中。这样,随着迭代进行,低半部分逐渐被确定的乘积位填充,而高半部分始终保持冗余形式,因此除了最后一次加法外,所有中间迭代均避免了进位传播,从而极大缩短了每个周期的延迟。)
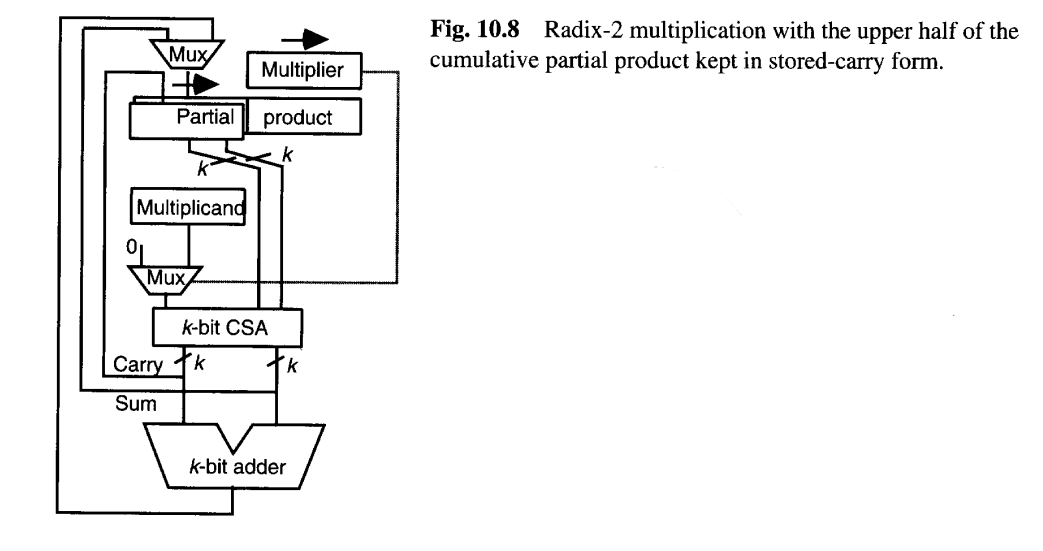
++现在,前k−1个周期中的每一个都可以变得更短,因为在这些周期中,信号仅通过对应于多路复用器和CSA的几个门级。特别地,这些周期中的延迟与字宽k无关++ 。与简单的顺序乘法器(图9.4)相比,实现图10.8中基于CSA的二进制乘法器所需的额外组件是一个k位寄存器、一个k位CSA和一个k位多路复用器;只有额外的k位寄存器在图10.7的设计中缺失。

图10.8的基于CSA的设计可以与基数4布斯重编码结合,将周期数减少50%(基4乘法每次处理2位乘数),同时使每个周期显著更快 。为实现此目的,图10.8设计中所需的变化如图10.9所示,其中需要一个小的2位加法器来将和的两个比特、进位的一个比特以及前一周期的进位组合成两个比特,这两个比特被移入累积部分积寄存器的后半部分(每次迭代后需要右移2位,因此需要从CSA输出中提取2个确定的乘积位),并产生新的进位供下一周期使用。2位加法器的进位输入的使用将在稍后解释。
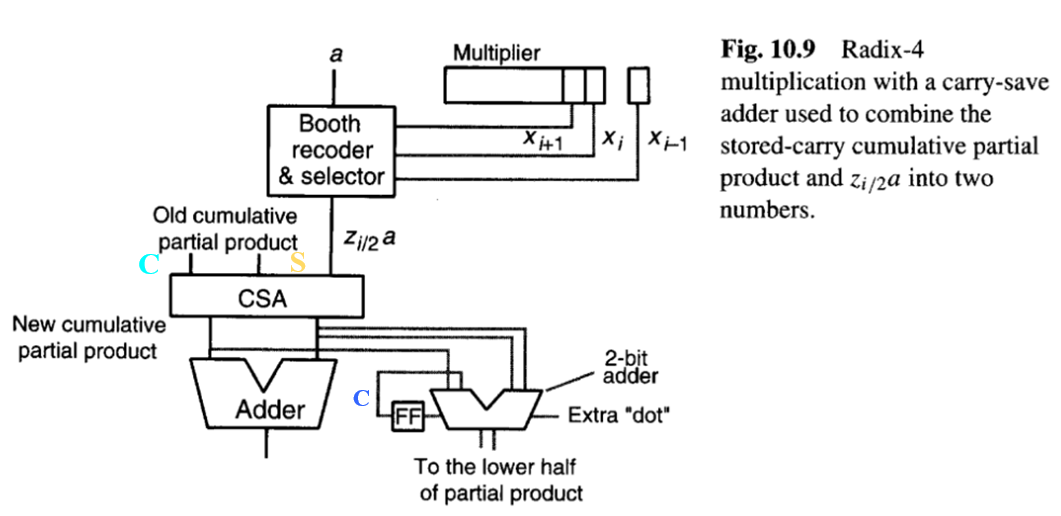
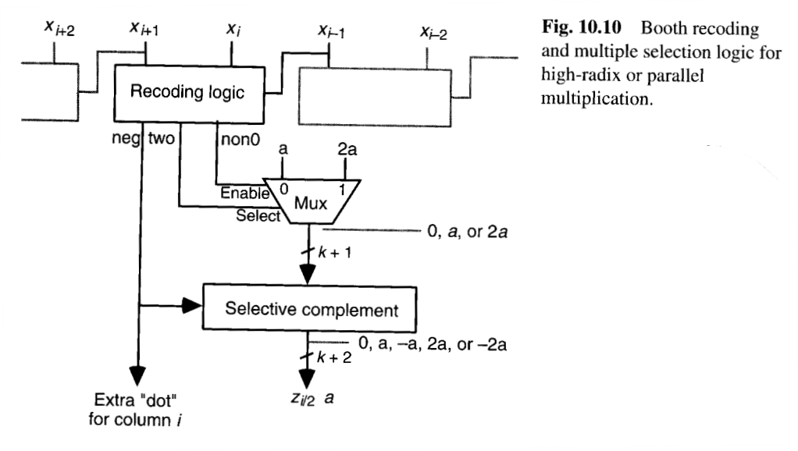
图10.9中的布斯重编码和倍数选择逻辑与图10.6中的设计不同,因为每个倍数的符号必须合并到倍数本身中,而不是作为一个控制加法/减法的信号。图10.10描绘了可用于高基数和并行乘法器的布斯重编码和倍数选择电路。
注意,在图10.10的电路中,负倍数−a和−2a是以2的补码格式生成的。通常,这是通过对a或2a进行按位取反并加1完成的。由xi和xi+1产生的倍数a或2a在右侧与位置i对齐,因此当被视为一个2k位数时,必须在其他右侧填充i个零。对这些零进行按位取反,然后在LSB位置加1,会将它们转换回零,并导致一个进位进入位置i。因此,我们可以继续忽略负倍数中的0到i−1位,并直接将额外的"点"插入到位置i。
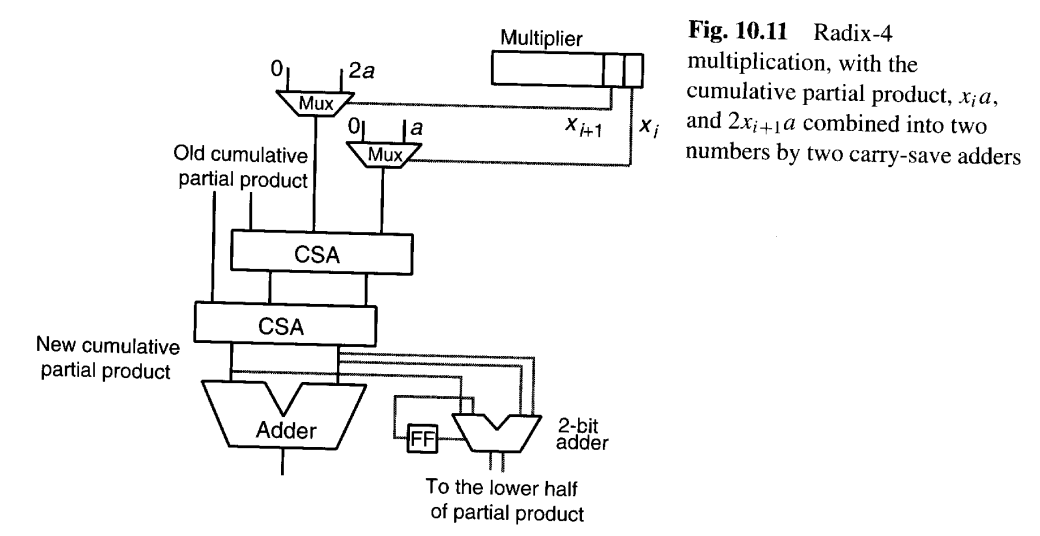
或者,可以不用布斯重编码,而使用图10.7中描述的方案来容纳所需的3a倍数。现在,需要组合四个数(累积部分积的和与进位分量、xia和2x(i+1)a),因此需要一个两级CSA树(图10.11)。
10.4 Radix-8 And Radix-16 Multipliers
从图10.11的基4乘法器出发,可以很容易地设想更高基数的乘法器。例如,一个基8的乘法器可能使用一个三级CSA树,将进位保留形式 的累积部分积与三个倍数xia、2x(i+1)a和4(xi+2)a合并成一个新的进位保留形式的累积部分积。然而,一旦我们使用了三层CSA,我们不妨再增加一层CSA来实现基16(即一次处理4位)的乘法器。由此产生的设计如图10.12所示。
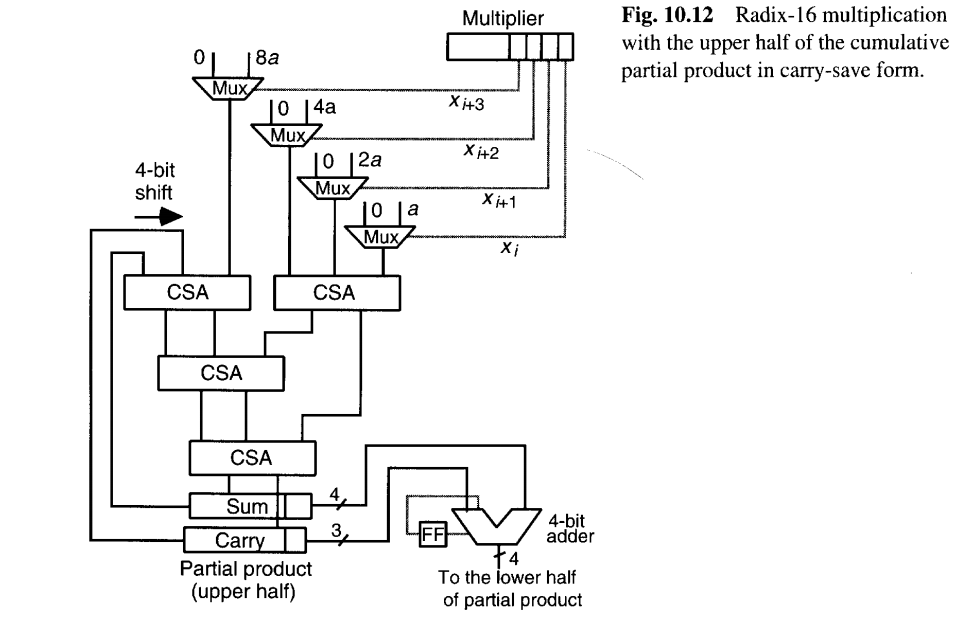
如果我们用布斯重编码和倍数选择电路替换图10.11中的每个多路复用器,可以得到另一种基数16乘法器。包括为CSA树的输入进行正确的对齐和符号扩展在内的乘法器设计细节。上述两种基数16乘法器(图10.12,或经过修改加入布斯重编码的图10.11)哪个更快或更具成本效益,取决于详细的电路级设计以及技术参数。
注意,在使用布斯重编码的基数2^b乘法中,我们必须将b/2个倍数减少为2个,这使用一个(b/2+2)输入的CSA树,该树的另外两个输入由进位保留部分积提供。如果不使用布斯重编码,则需要一个(b+2)输入的CSA树。是否使用布斯重编码是一个相当接近的权衡,因为布斯重编码电路和倍数选择逻辑比一个CSA稍慢,但在操作数数量上具有更大的压缩因子(2倍vs.1.5倍)。布斯重编码通过减少每个周期需要处理的倍数数量来简化CSA树,但这是以增加重编码电路的延迟和面积为代价的。
尽管前述选择多种多样,但并未穷尽设计空间。其他替代方案包括基数8和基数16布斯重编码,它们分别使用数字集[−4,4]和[−8,8]来表示乘数。我们将在章节末尾的问题中探讨重编码过程及相关的乘法器设计选项。例如请注意,在基8重编码下,我们需要处理±3a的倍数。和之前一样,我们可以预计算3a,或者将其表示为2a和a这对数,从而导致CSA树需要一个额外的输入。
当然,没有迫切的理由要停留在基数16。如果首先应用布斯重编码,可以使用类似图10.12的设计来实现基数256(一次处理8位)的乘法。这将要求将图10.12中的四个多路复用器替换为布斯重编码和选择逻辑。同样,这种新设计是否具有成本效益(例如,与获取乘数的7位并在一个四级CSA树中相加九个数相比)取决于具体技术,无法一概而论。
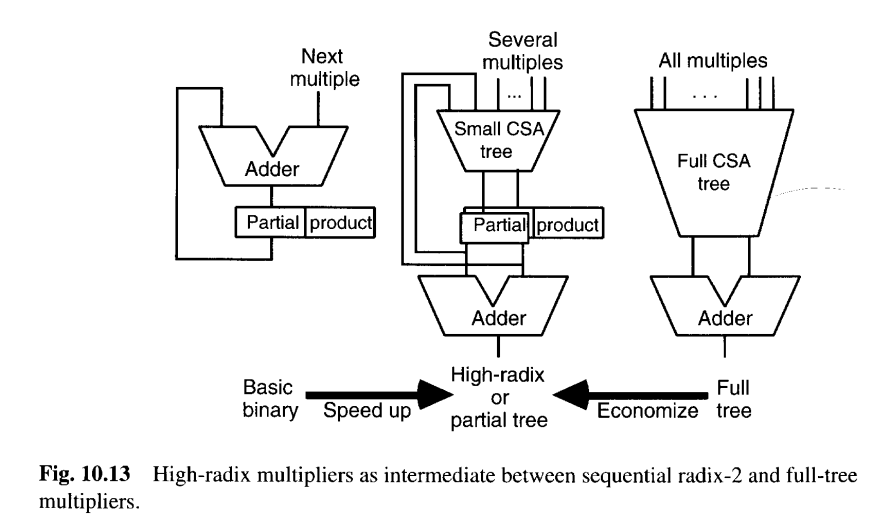
如图10.11和10.12所示的设计,可以看作是介于基本顺序(一次一位)乘法与第11章将要讨论的完全并行树形乘法器之间的中间方案。因此,高基数或部分树乘法器可以被视为既提供相对于顺序乘法的加速,又比完全并行的树形乘法器更经济的设计 (图10.13)。(相比顺序乘法 :通过一次处理多位(如4位)来减少周期数 ;相比完全并行树乘法 (第11章):它仍然使用迭代和反馈 (部分积寄存器),不是一次性将所有部分积相加,因此硬件(CSA树)规模较小,更经济,是性能与成本的折中。)
10.5 Multibeat Multipliers
在图10.8所示的基于进位保留加法器(CSA)的二进制乘法器中,CSA的输出被载入为其提供输入的同一个寄存器。一种常见的实现方法是使用主从触发器 作为寄存器。在这种方法中,每个寄存器有两部分:主侧 接受正在写入寄存器的新数据,而从侧(提供寄存器的输出)在时钟为高电平时在整个半周期内保持旧数据。当时钟变为低电平时,主侧的新数据被传送到从侧,为下一个周期做准备。在这种情况下,可能可以在主寄存器和从寄存器之间插入一个额外的CSA,而对时钟周期时间几乎没有影响。这实际上使部分积累积的速度加倍。

图10.14展示了一个一次处理3位的双节拍乘法器的示意图,它有效地在每个时钟周期内完成乘数的6位。这个使用基8布斯重编码的乘法器,类似于曼彻斯特大学MU5计算机中使用的双节拍设计[Gos171]。
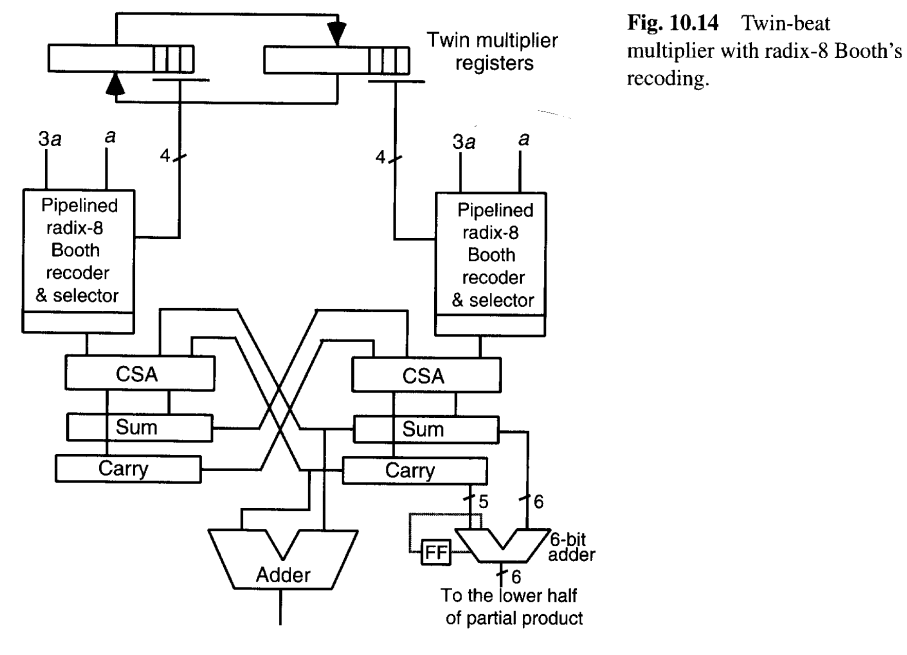
每个时钟周期被分为两个阶段或节拍。在第一个节拍,使用左侧的乘数寄存器确定下一个要加的倍数;在第二个节拍,使用右侧的乘数寄存器。每个周期(两个节拍)之后,图10.14右下角的小加法器确定乘积的6位,这些位被移入累积部分积寄存器的下半部分。这个加法器很可能比CSA慢;因此,为了使每个周期尽可能短,该加法器必须进行流水线化。由于乘积位一旦产生就不会改变,推导这些位的延迟对电路进位保留部分的其他计算没有影响。
笔者关于既然CSA延迟与位数无关,为什么不一次处理6位的思考,参考Deepseek:
处理更多位乘数的瓶颈不在于CSA,而在于倍数生成电路 。一次处理3位(基8), 使用布斯重编码后,需要生成的倍数为0、±a、±2a,±4a,得到这些倍数只需要移位和取反。一次处理6位(基64),即使使用布斯重编码,倍数集合会急剧扩大,并且会生成需要通过预计算加法得到的倍数,而这是需要避免的。
总结 "双节拍处理2次三位"优于"一次处理六位"的根本原因:
-
倍数生成复杂度:6位所需的倍数集合更复杂,需要额外的加法器预计算,增加延迟。
-
关键路径:整个乘法环路的延迟受最慢环节(重编码/倍数生成)限制,而非CSA。
-
面积效率:双节拍复用同一套简单硬件,面积接近基8乘法器,却实现了接近基64的吞吐量。
即通过增加时序复杂性(多节拍)来避免空间复杂性(庞大硬件)和逻辑复杂性(复杂倍数生成),从而实现性能、面积和功耗的平衡。
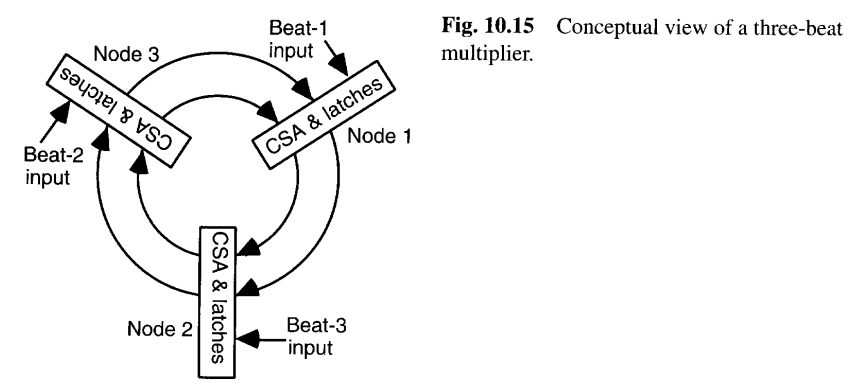
双节拍的概念可以轻松扩展以获得三节拍乘法器。通过将三个CSA和相关的锁存器放入一个环形中(图10.15),可以设想这样的设计,其节点由三相时钟驱动[deAn95]。每个节点需要两个节拍才能将其结果提供给下一个节点,从而导致奇数和偶数索引的部分积分别累积。最后,将四个操作数减少为两个操作数,然后将它们相加以获得最终乘积。
10.6 VLSI Complexity Issues
到目前为止,在第九章和第十章中描述的顺序基2和高基乘法器的实现是直接的。使用的部件包括进位保留加法器(CSA)、寄存器、多路复用器以及一个最终的快速进位传播加法器,这些都有标准设计可用。还需要少量的随机控制逻辑。请注意,每个输入之一接0的2选1多路复用器可以简化为一系列与门。
对于基2^b乘法器的CSA树,通常是先设计一个位片(bit slice),然后进行复制。如果不使用 Booth 重编码,CSA 树接收b+2个输入,所需的位片是一个(b+2:2)计数器。例如,一组 (7: 2)计数器片可用于实现不使用Booth重编码的基32乘法器的CSA树。如果首先应用基2^h Booth重编码,则每个周期的倍数数量会减少h倍,此时将需要一个(b/h+2:2)计数器片。
在执行基2^b乘法时,需要bk个两输入与门来并行形成每个周期的b个倍数。将这b个倍数缩减为2的CSA 树的面积复杂度为O(bk)。由于这些复杂度主导了最终快速加法器的复杂度,因此总体的面积需求为:
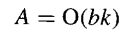
考虑到 CSA 树的对数高度(如第 8.3 节所述),乘法在k/b个周期内执行,每个周期的持续时间为O(logb),再加上一个需要O(logk)时间的最终加法。因此,总的时间复杂度变为:
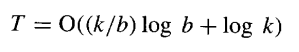
(以上推导假设无Booth编码。若使用基2^h Booth编码,则每个周期生成的倍数减少为b/h个,CSA 树输入数变为b/h+2,此时面积A:O(b/h*k),每个周期延迟:O(logb/h)(更小)。但总时间形式类似,只是常数因子改进。)
众所周知,任何计算两个k整数乘积的VLSI电路,其布局面积A和计算延迟T必须满足以下约束:AT至少与k√k成正比,且AT^2的增长速度至少与k^2 一样快。对于前面的实现,我们有:
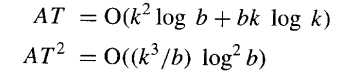
在复杂度范围的低端,即b为常数时,我们的乘法器的AT和AT^2度量分别为O(k^2)和O(k^3)。在另一个极端,即 b=k(此时一次考虑所有乘数位),我们有AT=O(k^2logk)和AT^2=O(k^2(logk)^2)。中间的设计不会产生更好的AT和AT^2值;因此,对于参数b的整个范围,这些乘法器在渐进意义上仍然是次优的。
根据通常被视为成本效益指标的AT度量,较慢的基2乘法器优于高基或树型乘法器。因此,在需要大量独立乘法的应用中,将可用的芯片面积用于大量慢速乘法器,而不是少量更快的单元,可能是合适的。
我们将在第 11 章中看到,通过更有效的流水线方案,高基乘法器的时间复杂度实际上可以从 O((k/b)logb+logk)降低到 O(k/b+logk)。尽管由此产生的设计带来了更好的AT和AT2度量,但前面的结论并未改变。
尽管这些负面结果表明高基和树型乘法器在渐进意义上是次优的,但鉴于字宽k在实践中相当有限,这样的设计对于参数b的广泛范围来说仍然是相当实用的。
总结:
-
基2^b乘法器:这是一种乘法器设计,每次迭代处理乘数的b个比特。b越高,所需的迭代次数k/b越少,但每个周期内的硬件(如生成倍数、CSA树)更复杂。
-
Booth 重编码:一种用于减少每个周期生成的被乘数倍数数量的技术。一个经典的h=3的基8 Booth编码,就是每3个比特(重叠1位)为一组。它将乘数比特分组并重新编码,使得每个周期只需要处理更少的倍数(从b+2减少到b/h+2),从而简化硬件(减少CSA 树的输入数)。
-
CSA 树:进位保留加法器树。用于将多个部分积快速压缩为两个数(通常是一个和向量和一个进位向量),而无需执行耗时的进位传播。其延迟与树高成正比,为 O(log(n))。n为加数数量。
Chapter 11 TREE AND ARRAY MULTIPLIERS
树形或完全并行乘法器构成了高基数乘法器(基数为2^k)的极限情况。通过一个高性能进位保留加法器树(CSA树)接一个快速加法器,可以实现对数时间的乘法。由此产生的乘法器成本高昂,但在乘法速度至关重要的应用中,这种设计是合理的。单侧CSA树产生了速度慢得多但结构高度规则的结构,称为阵列乘法器,它在提供比树形乘法器更高流水线吞吐量的同时,显著降低了芯片面积。
11.1 Full-Tree Multipliers
在最简单的形式中,并行或全树乘法器可以被看作是图10.12中设计的极端情况,其中被乘数的所有k个倍数被一次生成,并使用一个k输入的CSA树将它们归约为两个操作数进行最终加法。由于所有倍数在一次操作中合并,该树不需要反馈链路,使得流水线化非常可行。

图11.1显示了一个全树乘法器的总体结构。与被乘数a相关的各个倍数,对应于乘数x的二进制或高基数位或其重编码版本,在顶部形成。倍数生成电路可以是一组与门(二进制乘法器)、基4 Booth的倍数生成器(重编码乘法器)等等。这些倍数在一个组合逻辑的部分积归约树中被相加,该树以冗余形式产生它们的和。最后,冗余结果在底部被转换为标准的二进制输出。
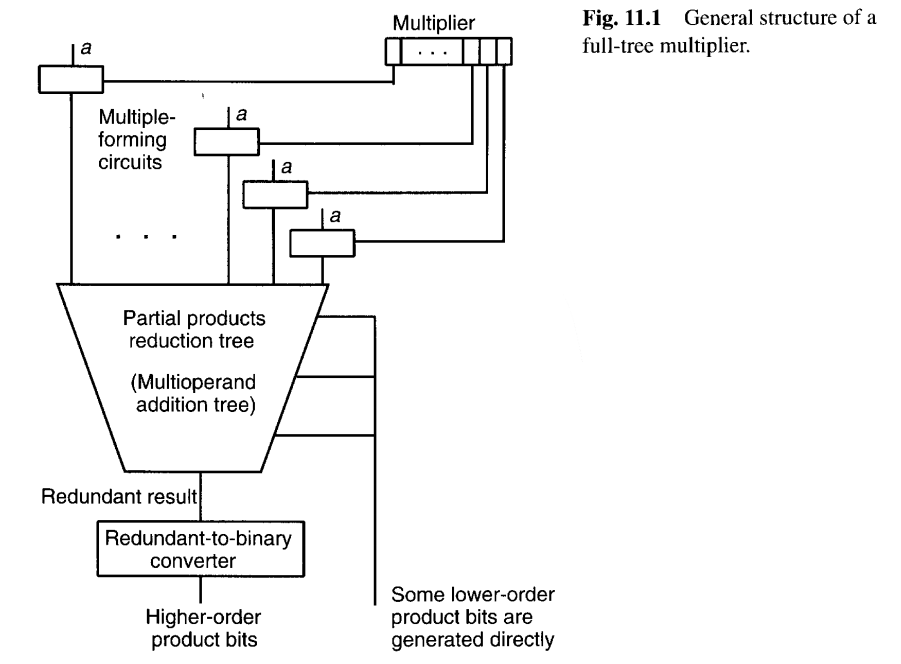
目前为止已经构建或提出了多种类型的树形乘法器。这些乘法器通过图11.1中的以下三个元素的设计来区分:
- 倍数生成电路 :负责根据乘数位生成被乘数的相应倍数
- 部分积归约树 :用于将大量部分积(由倍数生成电路产生)快速压缩为少数几个数(通常两个),采用CSA树实现。归约树的优化直接影响乘法器的速度和面积。
- 冗余到二进制转换器 :由于CSA树输出的是进位保留形式的冗余数(和与进位),需要用一个快速加法器(如超前进位加法器)将其转换为标准的二进制数,得到最终乘积。
在本节的剩余部分,我们重点讨论涉及无符号二进制倍数和CSA归约树的树形乘法器变体。由于冗余结果以进位保留形式存在,最终的转换器就是一个快速加法器。第11.2节讨论了与前述倍数生成和归约方案的偏离。有符号树形乘法器在第11.3节中介绍。
根据我们在第9章和第10章对顺序乘法的讨论,我们知道如何形成部分积,以及如何通过使用高基方法减少部分积的数量。高基乘法器中提到的权衡在这里也存在:更复杂的倍数生成电路可以导致归约树的简化。再次强调,我们一般不能说哪种组合会导致更高的成本效益,因为权衡的确切性质取决于设计和技术。
回顾第8.3节讨论的构建CSA树的Wallace和Dadda策略,这分别产生了Wallace和Dadda树乘法器。本质上,Wallace构建CSA树的策略是尽早组合部分积位,而Dadda的方法是尽可能晚地组合,同时保持CSA树的关键路径长度不变。Wallace的方法导致可能的最快设计,而Dadda的策略通常导致更简单的CSA树和更宽的进位传播加法器。
作为一个简单的例子,我们推导4×4乘法的Wallace和Dadda树乘法器。图11.2以表格形式展示了设计过程和结果,其中的整数表示各列中剩余的点数。每个设计以16个与门开始,形成xiaj项或点,0≤i, j≤3。得到的16个点分布在七个列中,模式为1, 2, 3, 4, 3, 2, 1。Wallace树设计在第一级需要3个全加器(FA)和1个半加器(HA),然后在第二级需要2个FA和2个HA,最后是一个4位进位传播加法器。对于Dadda树设计,我们的首要目标是将部分积点阵的高度从4降低到3 ,因此第一级需要2个FA。随后是第二级的2个FA和2个HA**(将高度从3降低到2)**,最后是一个6位进位传播加法器。
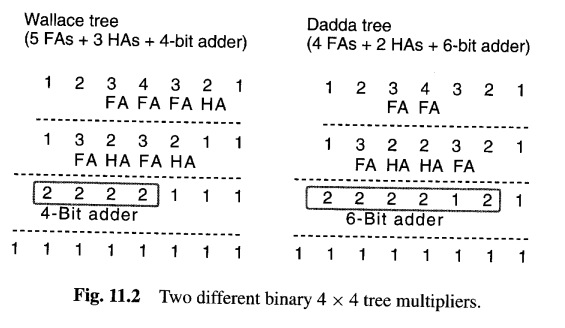
Wallace和Dadda之间的中间方法产生了各种提供速度-成本权衡的设计。例如,可能Wallace树和Dadda树都不能得到一个方便宽度的快速加法器。在这种情况下,混合方法可能会产生最佳结果。
注意,第8章介绍的进位保留多操作数加法的结果几乎无需修改就适用于部分积归约树的设计。所需的唯一修改源于要相加的操作数的相对移位。例如,在图8.12中,我们看到在添加七个右对齐的k位操作数时,CSA都是k位宽。在一个7×7树乘法器的七操作数CSA树中,输入操作数以0到6位的移位出现,导致如图11.3顶部所示的输入配置。我们看到移位的输入需要在树的底部使用稍宽的块。比较图11.3和图8.12,注意所有差异,是有启发性的。(部分积归约本质上是多操作数加法问题,但操作数存在移位(对应乘法中的权重)。因此,CSA树的设计需考虑位宽扩展和不对齐的情况,导致树底部的加法器位宽更大)


当然,没有强制理由将输入或中间操作数的所有位保持在一起并馈送到多位CSA,这会导致使用许多半加器,这些半加器只是重新排列点而不有助于它们的归约。如图11.2所示,使用单位FA和HA进行归约会导致更低的复杂度,甚至可能更快的速度。推导出执行图11.3电路相同功能的Wallace和Dadda树乘法器留作练习。
从图11.3或其等效的Wallace树和Dadda树可以清楚地看出:基于CSA的对数深度归约树具有不规则的结构,这使得其设计和布局相当困难。 此外,不同长度的连接和信号路径导致逻辑冒险和信号偏移,对性能和功耗都有影响。**在VLSI设计中,我们努力构建由迭代或递归结构组成的电路,这些结构有助于高效自动的综合和布局。**接下来将讨论更适合VLSI实现的替代归约树。
11.2 Alternative Reduction Trees
回顾我们在第8.5节的讨论,可以设计一个(7:2)计数器切片,该切片以同一列 i 的7个比特作为输入,并在列 i 和 i+1 各产生一个比特作为输出。这种切片在适当复制后,可以执行图11.3中归约树部分的功能。当然,图11.3中并非所有列都有七个输入。为了规则性,可以保持前述迭代电路不变并提供虚拟的0输入,或者通过移除每个切片中的冗余部分来进行修剪。这种优化完全在自动化设计工具的能力范围内。
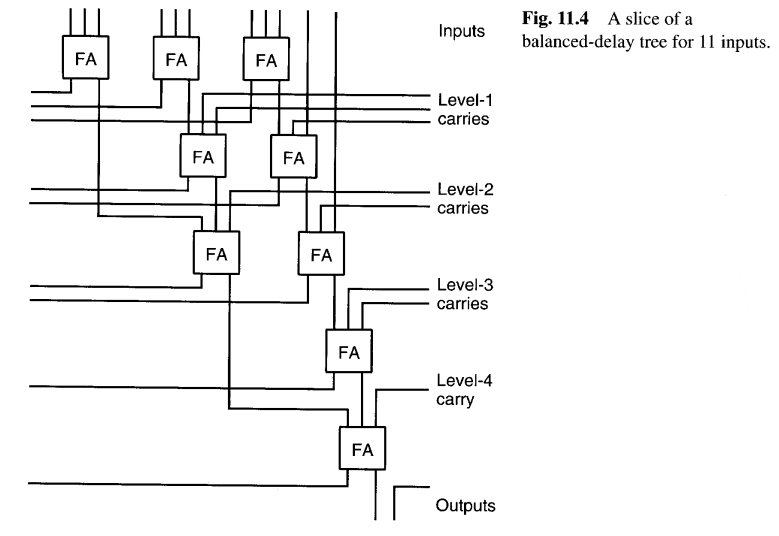
根据表8.1,一个(11:2)计数器至少有五个全加器级。图11.4展示了一种特定的五级全加器排列,用于执行11到2的归约,其特点是所有输出在相同的全加器延迟后产生。注意在第i级产生的所有进位如何进入第i+1级的全加器。图11.4中的全加器可以布局成占据一个狭窄的垂直切片,然后可以复制以形成所需宽度的11输入归约树。这种平衡延迟树非常适合并行乘法器的VLSI实现。

图11.4的电路由三列组成,从左到右分别包含1、3和5个全加器。现在很容易看出,只需在电路右侧附加一列7个全加器,就可以将输入数量从11扩展到18。新增列顶部的全加器将容纳三个新输入,而其他全加器(除了最底部的两个)每个可以接受一个新输入;后面的这些全加器还必须容纳来自上方的和以及来自右侧的进位。注意,各列中的全加器或多或少是独立的,因为相邻列仅由一根导线连接。这一特性使得电路可以在一个狭窄的切片中布局,而不需要为互连预留大量空间。
与使用CSA或(3:2)计数器构建部分积归约树不同,可以使用一个将四个数减少为两个数的模块作为基本构建块。然后,部分积归约树可以构造成二叉树,这种结构具有递归性,使其更加规则且更容易布局(图11.5)。图11.6展示了一种可能的布局方式,用于图11.5的七个模块的树。注意,向图11.6的树中添加一级需要复制该树并在它们之间插入一个4到2归约模块。
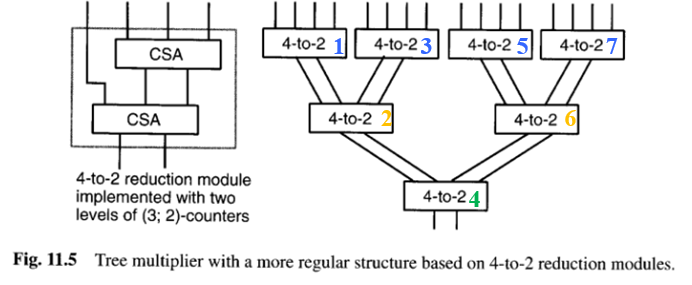
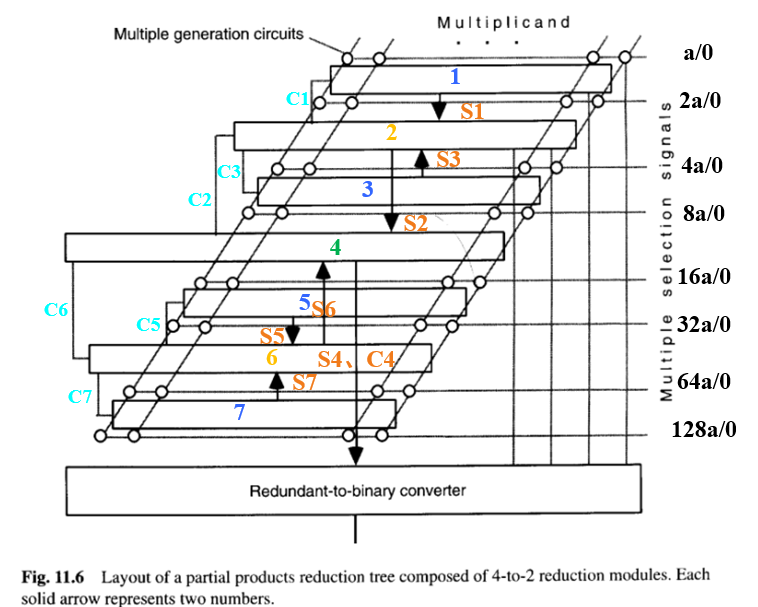
在图11.6中,第一、第三、第五和第七个矩形框对应于图11.5的顶层块。这些块接收被乘数的四个倍数,并将它们减少为一对数,供第二和第六块使用。后面的每个块依次向第四块提供两个数,第四块则馈入冗余到二进制转换器。
如果4到2归约模块内部由两级CSA组成,如图11.5所示,那么二叉树结构中的CSA级数可能比Wallace树或Dadda树更多。然而,互连的规则性以及由此产生的高效布局,可以充分补偿由于电路深度增加而带来的额外逻辑延迟。
注意,用于二进制操作数的4到2归约电路可以视为一个用于基数为2、数字集为[0,2]的GSD加法器,其中数字用以下2比特编码表示:
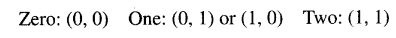
这种二叉树归约方案的一个变体基于二进制有符号数字(BSD)表示,而不是进位保留表示。这些部分积通过一个BSD加法器树进行组合,以BSD形式获得最终乘积。然后通过BSD到二进制转换器获得标准二进制结果,这本质上是一个快速减法器,用于从BSD数的正部分减去其负部分。BSD部分积的一个好处是,可以轻松处理由2的补码数中的符号位产生的负倍数(参见第11.3节)。某些低效性源于用于容纳数字符号的额外比特在大多数正倍数中被浪费。
当然,进位保留和BSD数并不是唯一允许通过有限进位加法进行快速归约的数字表示。根据技术能力和限制,还有其他几种数字集可能提供某些优势[Parh96]。例如,使用数字集[0,3]的基2部分积适用于高效的并行进位加法过程,同时可以容纳三个而不是一个或两个二进制乘法的倍数。有趣的是,从冗余数字集[0,3]到[0,1]的最终转换并不比从[0,2]到[0,1]的转换困难。
显然,任何用于构建CSA树的方法都可以与基2^b Booth重编码结合以减少树的大小。然而,对于现代VLSI技术,在树乘法器中使用Booth重编码受到质疑;似乎压缩k个数(而不是k/b个数)所需的额外CSA可能比Booth重编码逻辑更简单,特别是当考虑到布线和由于不规则性及非均匀性带来的开销时。(对于现代工艺,布线延迟占主导,规整的CSA树(即使更大)可能比不规则的Booth树更快,自动布局布线工具对规整结构优化更好。)
11.3 Tree Multipliers For Signed Numbers
当直接进行2的补码乘法时,每个待加的部分积都是有符号数。因此,为了使CSA树能正确输出其输入的和,每个部分积都必须符号扩展到最终乘积的位宽。回顾我们在第8.6节中关于有符号多操作数加法的讨论,其中假设2的补码操作数的最低有效位(LSB)对齐。特别地,参考图8.18中基于符号扩展(硬件共享)和将负位转换为正位的两种可能方法。

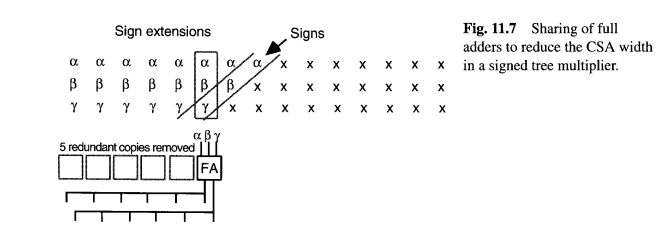
对于2的补码部分积的加法,考虑是类似的,唯一的区别在于移位。图11.7描绘了一个包含三个符号扩展部分积的例子。我们看到,这里同样可以用一个全加器产生多个不同列所需的结果。如果将此过程应用于部分积位矩阵的所有行,所得的结构将比假设操作数为无符号时稍微复杂一些。注意,由于移位,图11.7中的重复次数比图8.18少,因此为容纳符号而进行的宽度扩展会略大一些。
另一种方法由Baugh和Wooley提出,效率更高,因此通常以其原始形式或修改形式用于2的补码乘法。为了理解这种方法,我们从图11.8a的无符号乘法开始,并注意在2的补码表示中,符号位的负权重必须被考虑以获得正确的乘积(图11.8b)。为了避免处理部分积矩阵中负权重的位,Baugh和Wooley建议按图11.8c所示的方式修改位,在此过程中向位矩阵添加了一些条目。

Baugh-Wooley策略将最大列高度增加了2,因此可能导致通过CSA树的延迟更大。例如,在图11.8描绘的5×5乘法中,列高度从5增加到7,导致需要额外的一级CSA。**然而,在这个具体例子中,可以通过从第4列移除x4条目,并在只有四个条目的第3列放置两个x4条目来避免额外延迟。**这样将高度降低到6,仍然可以由三级CSA树处理。
为了证明Baugh-Wooley方案的正确性,让我们聚焦于图11.8中的条目a₄x̄₀。考虑到2的补码数中符号位的负权重,该条目本应是 -a₄x₀。我们注意到:
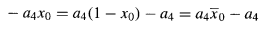
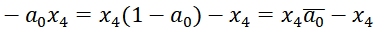
因此,我们可以用两个条目a₄x̄₀和-a₄替换-a₄x₀ 。如果使用条目a₄而不是 -a₄,则列和增加了2a₄。为了补偿这一点,我们必须在下一个更高列中插入 -a₄。同样的论证可以对a₄x̄₁、a₄x̄₂和a₄x̄₃重复进行。除第一列外的每一列都得到一个a₄和一个 -a₄,它们相互抵消。p₈列得到一个-a₄条目,可替换为ā₄ - 1。**同样的论证可重复用于āᵢx₄条目,从而在第p₄列插入x₄,在第p₈列插入x̄₄ - 1。**这样在第八列产生的两个-1等价于p₉列中的一个-1条目,而p₉列的-1又可替换为一个1和一个向不存在的(无关紧要的)第十列的借位。
另一种证明Baugh-Wooley方法合理性的方式是将所有权重为负的a₄xᵢ项(0 ≤ i ≤ 3)移到底行,从而导致最后两行出现两个负数(即前面的数和由aᵢx₄位形成的数,0 ≤ i ≤ 3)。现在,需要从所有正元素的和中减去这两个数x₄和a₄x。我们不是减去x₄ × a,而是加上x₄乘以a的补码,即a的反码加上x₄(类似地对于a₄x)。读者应能补充其他细节。
Baugh-Wooley方法的一种修改形式(图11.8d)更可取,因为它不会导致最大列高度的增加。证明这种修改形式的合理性留作练习。
11.4 Partial-Tree Multipliers
如果全树乘法器的成本对于特定应用来说过高,那么可以考虑各种混合串并行的设计方案。设h是一个小于k的数。一种思路是,重复[k/h]次使用一个较小的CSA树,来完成k×k乘法所需的k个操作数的加法。图11.9显示了由此产生的设计,它包括一个用于累加部分积(以存储进位形式)和h个新操作数的(h+2)输入CSA树,并将得到的和与进位反馈回来,以便与下一批h个操作数结合。
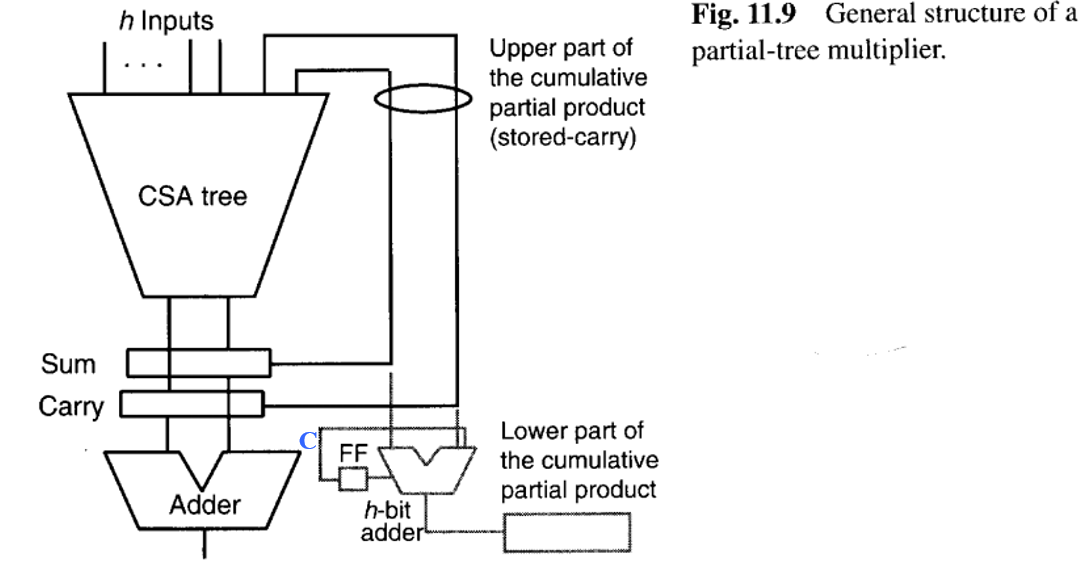
由于下一批h个操作数将相对于当前批移位h位,因此在每次处理后,可以释放(确定) 计算出的和中的h位以及进位中的h−1位。这些位使用一个h位加法器相结合,产生h位的最终乘积,进位输出保存在一个触发器中,以便与下一次的输入结合。或者,可以通过简单地在各自的寄存器中将这些释放的位右移,并将转换为标准二进制格式的操作推迟到最后,从而将它们保持在进位保留形式中。这就是为什么图11.9中的部分内容以虚线形式呈现。如果由于其他原因,ALU中已经有一个快速的双倍位宽加法器,则可以采用后一种方法。
请注意,图11.9描绘的设计对应于基2^h乘法。因此,第10.3和10.4节的讨论在这里也相关。实际上,高基乘法和部分树乘法器之间的差异是量上的而非质上的 (见图10.13)。**当h相对较小时,比如最多8位,我们倾向于将图11.9的乘法器视为高基乘法器。另一方面,当h是k的很大一部分时,比如k/2或k/4,那么我们将该设计视为部分树乘法器。**在第11.6节中,我们将看到,当h很大时,图11.9设计的一种流水线变体可以快得多。
图11.9是基于基2乘法的假设绘制的。如果首先应用基2^b的Booth重编码,为乘数的每b位生成一个倍数,那么所需的处理次数将减少b倍,并且每次处理后可以释放bh位。因此,图11.9中的小加法器宽度将为bh位。
11.5 Array Multipliers
考虑一个全树乘法器(图11.1),其中归约树是单侧的,且最终加法器采用行波进位设计,如图11.10所示。这种由最慢可能的CSA树和最慢可能的进位传播加法器组成的树状乘法器,被称为阵列乘法器。
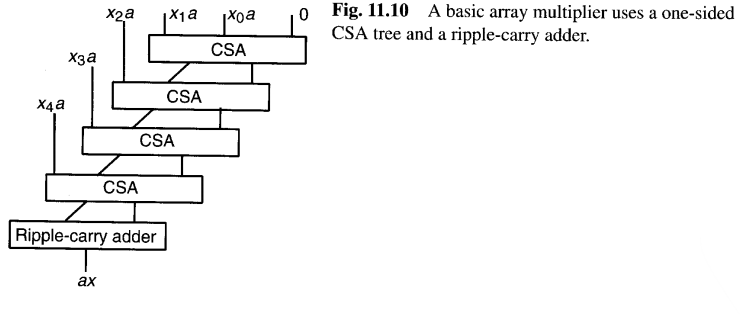
但是,为什么会有人对这种慢速乘法器感兴趣呢?答案是,阵列乘法器结构非常规则 ,并且只使用从一个全加器到水平、垂直或对角相邻全加器的短连线。因此,它在VLSI中具有非常简单高效的布局。此外,通过在每个CSA之后或每几行之后插入锁存器,它可以被轻松高效地流水线化(最后一行必须不同处理,如第11.6节所述,因为其延迟远大于其他行)。
图11.10阵列乘法器中最顶部CSA的空闲输入端可用于实现一个产生 p = ax + y 的乘加模块。这在涉及卷积或内积计算的各种应用中很有用。当只需要计算 ax 时,可以移除图11.10阵列乘法器中最顶部的CSA,将 x0*a 和 x1*a 直接输入到第二个CSA。
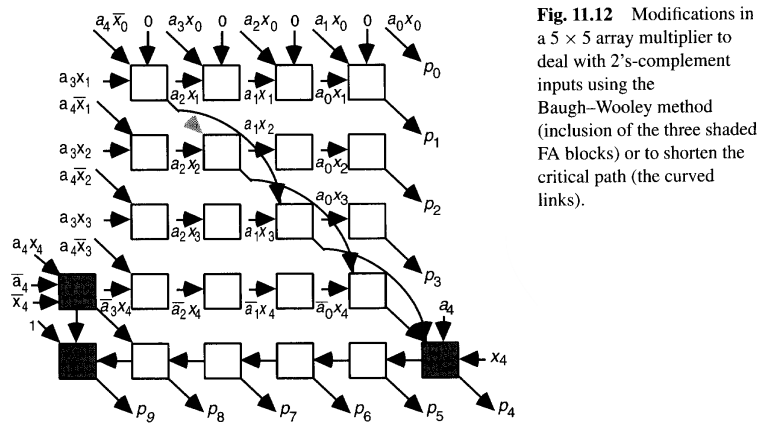
图11.11展示了使用全加器单元和两输入与门设计的 5×5 阵列乘法器。和输出对角连接 ,进位输出垂直连接 (最后一行除外,在那里它们从右到左链接)。图11.11的设计假设是无符号数,但使用Baugh-Wooley方法可以轻松转换为二进制补码阵列乘法器。这需要在行波进位加法器的右端增加一个全加器来处理 a4 和 x4 项,并在左下边缘增加几个全加器来容纳 ā4、x̄4 和 1 项(见图11.12)。图11.12中FA模块之间的大部分连接已被移除以避免杂乱。


鉴于基于Baugh-Wooley方法的二进制补码阵列乘法器(图11.12)的简单性,我们不再使用Pezaris等人提出的技术,那些技术要求在某些阵列位置使用全加器单元的变体,这些变体需要能容纳一些负权重输入比特并产生一个或两个负权重输出。
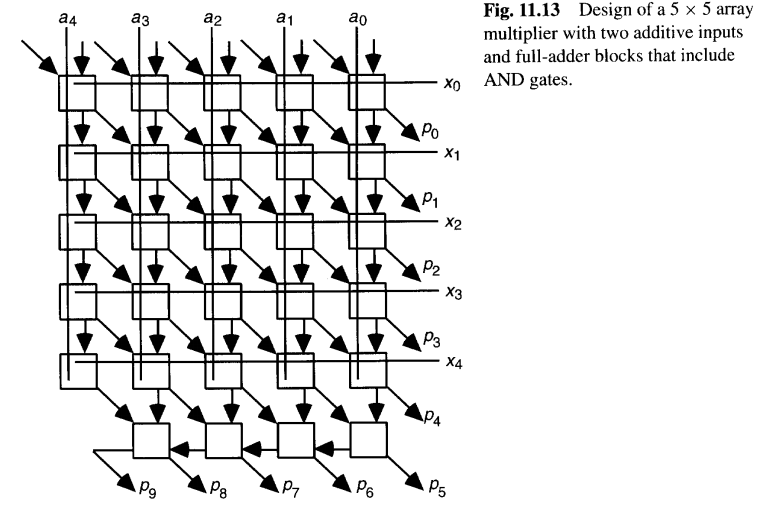
如果我们构建一个包含全加器和与门的单元来内部形成项 aj * xi,图11.11的无符号阵列乘法器就变成了图11.13。这里,xi 和 aj 比特被广播到单元的行和列 ,第 i 行、第 j 列的单元形成项 aj * xi 并将其用作其FA的输入。如果需要,可以通过用与门替换第一行或前两行中的单元来降低设计复杂度。
一个k×k阵列乘法器的关键路径 ,当全加器模块的和生成逻辑延迟大于进位生成电路延迟时,会沿着图11.12中的主对角线(从左上到右下)延伸,并在最后一行水平延伸到p9输出。因此,可以通过重新排列全加器的输入来减少阵列乘法的整体延迟,使得一些和信号跳过中间行(即从第i行直接连接到第 i+h行,其中 h>1)。
图11.12展示了当h=2时,在主对角线上修改后的连接方式。现在,最右下角的单元多了一个输入,但我们可以将其中一个输入重定向到主对角线上的第二个单元,该单元现在恰好有一个空闲输入。然而需要注意的是,这种跳级的做法会导致布局规整性下降,同时也需要更长的连线,因此在实践中可能并非一项值得的修改。
由于阵列乘法器近一半的延迟来自最后一行的单元,考虑能否更快地完成最终加法是很有趣的。显然,可以用一个快速加法器替换最后一行单元,但这会影响设计的规整性。此外,即使是一个快速加法器仍然比其他行慢得多,使得流水线化更加困难。
为了了解如何消除阵列乘法器的行波进位部分,让我们将 k^2 个项 ajxi 排列成一个三角形,其中的比特按照以下模式分布在2k−1列中:
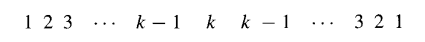
乘积的最低有效位直接输出,而其他位则通过一行行的全加器和半加器(图11.14中的矩形框)逐步归约。让我们关注第i级,并假设前i−1级已经产生了超过Bi边界的最终乘积位的两个版本:一个版本假设下一次进位保留加法将产生一个跨越Bi的进位,另一个版本则假设没有进位(图11.15)。
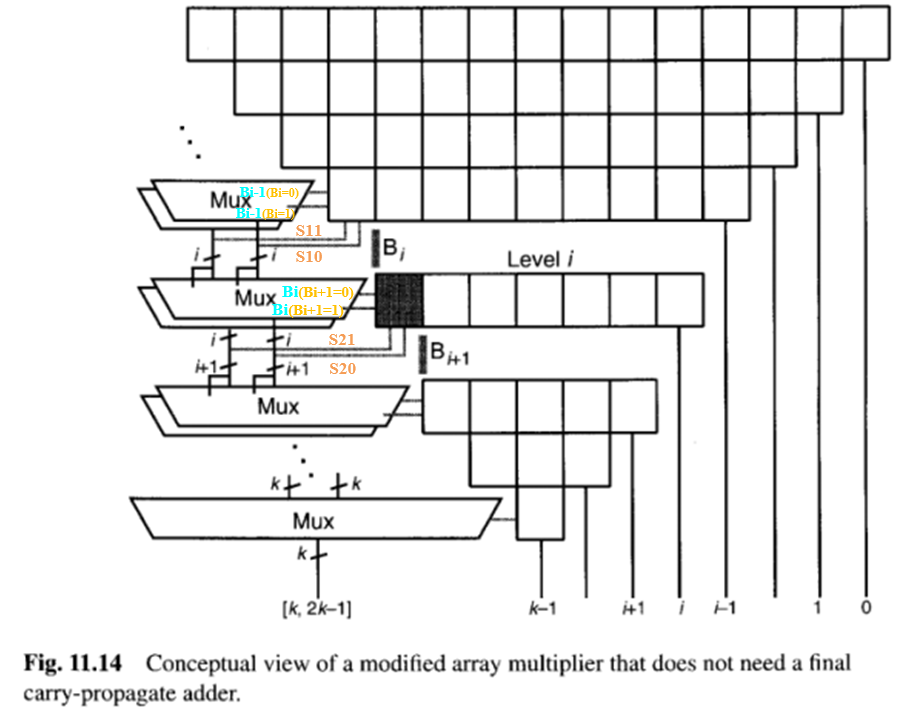
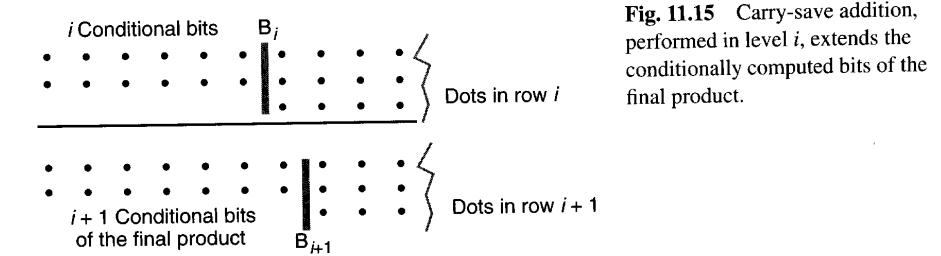
在第i级,图11.14中的阴影块 会根据未来跨越Bi+1边界是否有进位,产生其和与进位的两个版本 (条件版本)。来自阴影块的条件和比特被简单地附加到来自上方的i个比特之后 。这样,我们就获得了乘积的高i+1位的两个版本,其条件取决于未来跨越Bi+1边界的进位。然后,这个过程在更低的级别中重复,每一级都将条件计算部分的长度扩展一位,最终的多路复用器以非冗余形式提供最终乘积的最后k位。
图11.14所示的概念设计经过特定优化以消除冗余元件后,可转化为实际的乘法器电路[Erce90,Cimi96]。
11.6 Pipelined Tree And Array Multipliers
一个完整的树型乘法器可以很容易地实现流水线化。其部分积归约树是一个组合电路,可以被切割成多个流水线级。然而,对于图11.9中的部分树型乘法器,必须等到前一组输入的和与进位被锁存后,才能施加新的输入集。考虑到对于较大的h,树的深度可能相当显著,施加输入到树的速率,从而乘法器的速度,就会受到限制。
现在,如果我们不是将树输出反馈到其输入端,而是像图11.16所示那样,将其反馈到(h+2)输入树的中间,那么流水线的速率将仅由两个CSA(进位保存加法器)级的延迟决定,而不是整个树的深度。这带来了更快的乘法运算。
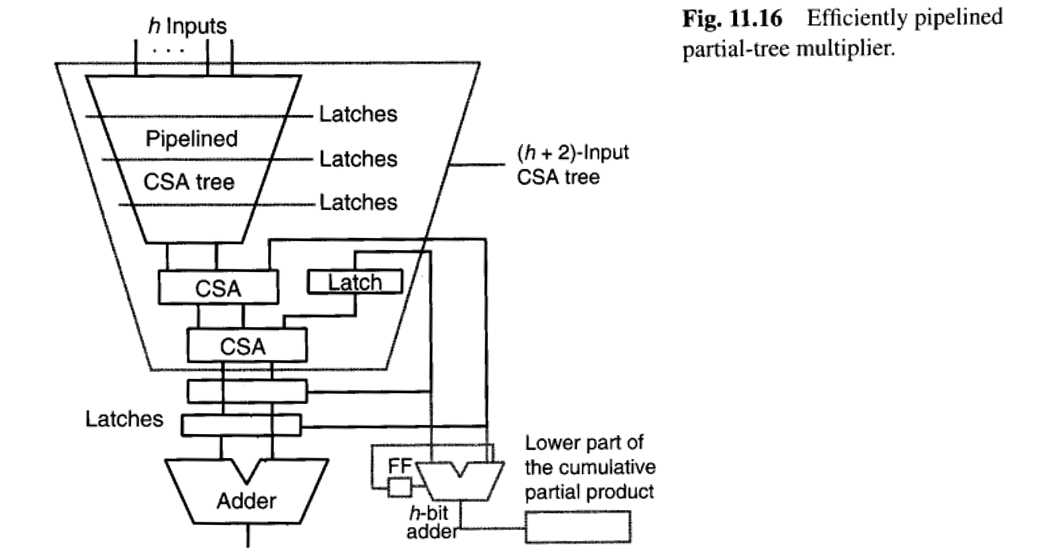
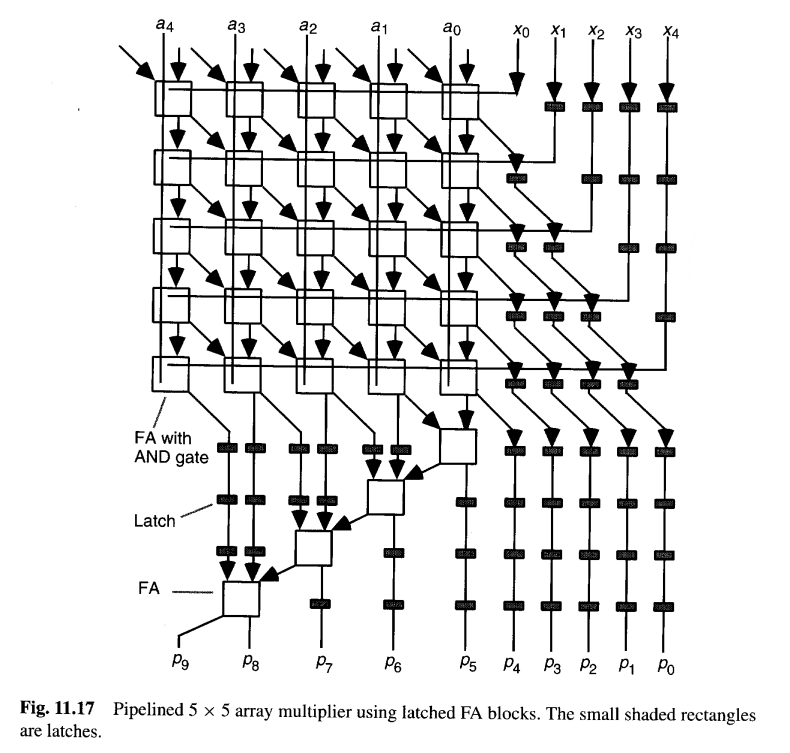
图11.17展示了对阵列乘法器进行流水线化的一种方法。输入从上方施加,乘积在九个时钟周期(一般情况为2k−1个周期)后从下方输出。这里使用的FA块假定其和与进位输出端都带有锁存器。请注意,阵列乘法器各层所需的xi输入是如何通过在路径中插入锁存器来延迟的,以及图11.13底部那个4位行波进位加法器在图11.17中是如何被流水线化的。