PID 控制算法 | 连续域原理、离散化实现及工程应用

斐夷所非2026-01-18 9:59

注：本文为 "PID 控制算法" 相关合辑。

图片清晰度受引文原图所限。

略作重排，如有内容异常，请看原文。

PID 控制算法（一）------连续控制系统的 PID 算法及 MATLAB 仿真

引言

PID 是 Proportional（比例）、Integral（积分）、Differential（微分）三者的缩写。

PID 调节是连续控制系统中技术成熟度高、工程应用范围广的调节方式。

PID 调节的本质为：依据输入的偏差量，按照比例、积分、微分的函数关系完成运算，将运算结果作为被控对象的控制输出量。

此前在工程实践中虽多次应用 PID 算法，但对其原理的理解尚不完善，参数整定也多为经验性调试。经系统性学习后形成对 PID 控制的新认知，现整理记录以供参考。

连续系统的 PID 控制

PID 控制的逻辑为：将误差信号 e ( t ) e(t) e(t) 的比例（P）、积分（I）与微分（D）分量做线性组合，构建系统的控制量完成闭环调节，其连续域的输出控制量表达式为：

u ( t ) = K P [ e ( t ) + 1 T I ∫ 0 t e ( t ) d t + T D d e ( t ) d t ] u(t) = K_P\left[e(t) + \frac{1}{T_I} \int_{0}^{t} e(t)\mathrm{d}t + T_D \frac{\mathrm{d}e(t)}{dt}\right] u(t)=KP[e(t)+TI1∫0te(t)dt+TDdtde(t)]

该时域表达式中参数定义：

  • K p K_p Kp ------ 比例系数：用于放大/缩小误差信号，直接影响系统的响应速度与超调量
  • T I T_I TI ------ 积分时间常数：反映积分环节的作用强度，决定稳态误差的消除速率
  • T D T_D TD ------ 微分时间常数：反映微分环节的作用强度，用于预判误差变化趋势
  • e ( t ) e(t) e(t) ------ 系统偏差信号：时域下的输入量，为参考值与系统实际输出值的差值（即 e ( t ) = r ( t ) − y ( t ) e(t) = r(t) - y(t) e(t)=r(t)−y(t)， r ( t ) r(t) r(t) 为参考输入， y ( t ) y(t) y(t) 为系统输出）
  • u ( t ) u(t) u(t) ------ 控制器输出控制量：时域下的输出量，用于调节被控对象的运行状态

对该时域表达式进行拉普拉斯变换并整理后，可得模拟 PID 调节器的传递函数：
D ( s ) = U ( s ) E ( s ) = K p ( 1 + 1 T I s + T D s ) D(s) = \frac{U(s)}{E(s)} = K_p\left(1 + \frac{1}{T_I s} + T_D s\right) D(s)=E(s)U(s)=Kp(1+TIs1+TDs)

该复频域表达式中参数定义：

  • D ( s ) D(s) D(s) ------ 模拟 PID 调节器的传递函数：描述复频域下控制器输出与输入的比值关系，用于分析系统的稳定性与动态特性
  • U ( s ) U(s) U(s) ------ 控制器输出控制量的复频域表示：由 u ( t ) u(t) u(t) 经拉普拉斯变换得到
  • E ( s ) E(s) E(s) ------ 系统偏差信号的复频域表示：由 e ( t ) e(t) e(t) 经拉普拉斯变换得到
  • s s s ------ 复频率变量：拉普拉斯变换中的复频域符号，用于将时域信号转换为复频域信号


\qquad\qquad\qquad 模拟 PID 控制系统框图

对 PID 参数的理论解析

由连续域 PID 控制的数学表达式，可对比例、积分、微分三个环节的控制特性做如下解析：

比例控制 K p K_p Kp

比例环节的作用为将误差信号 e ( t ) e(t) e(t) 按系数 K p K_p Kp 线性放大/缩小，能够提升系统的动态响应速率，实现对误差的快速反馈与抑制，但无法消除系统的稳态误差 。
K p K_p Kp 取值越大，系统响应越快，跟踪误差的能力越强，但易引发系统超调量增大； K p K_p Kp 取值越小，系统响应越迟缓，虽超调量减小，但调节效率降低。当 K p K_p Kp 超过临界值时，闭环系统将丧失稳定特性，出现持续振荡。

积分控制 K i K_i Ki

积分环节的作用为消除系统的稳态误差 ，其控制逻辑为：只要系统存在偏差信号，积分环节便会对偏差进行时间累积，持续输出控制量直至偏差归零，积分作用才会停止。

积分作用的强度与系统动态特性负相关：积分作用过强，会显著增大系统的超调量，甚至诱发系统等幅振荡；积分作用过弱，稳态误差的消除速率变慢，系统进入稳态的过渡时间延长。积分环节的本质存在滞后特性，其调节动作始终基于已产生的偏差累积，无法对偏差的变化趋势做预判。

微分控制 K d K_d Kd

微分环节的输出与误差信号的变化率 d e ( t ) d t \frac{\mathrm{d}e(t)}{\mathrm{d}t} dtde(t) 成正比，其物理意义为对误差的变化趋势进行预判，因此也被称为系统的「超前校正环节」。

微分环节可有效减小系统超调量、抑制振荡，提升闭环系统的稳定裕度，同时能加快系统的响应速度，优化整体动态性能。微分环节与积分环节形成互补特性：积分环节对历史偏差做累积补偿，微分环节对未来偏差做超前预判，二者结合可大幅优化控制系统的综合性能。

基于 MATLAB 的 PID 控制仿真分析

为直观验证各环节的控制特性，通过 MATLAB 软件搭建控制系统模型，完成 PID 各环节的仿真验证。本次仿真选取二阶惯性环节作为被控对象，其开环传递函数为：

G ( s ) = 2 ( 3 s + 1 ) ( 2 s + 1 ) G(s)=\frac{2}{(3s+1)(2s+1)} G(s)=(3s+1)(2s+1)2

比例控制

比例控制的输出量与输入偏差量呈线性比例关系，本质为对误差信号的幅值缩放，其传递函数为：
G ( s ) = K p G(s) = K_p G(s)=Kp

选取多组不同的比例系数，绘制闭环系统的单位阶跃响应曲线，仿真代码如下：

matlab 复制代码 
Gs = tf(2,conv([3,1],[2,1]));           % 定义被控对象传递函数，conv()实现多项式相乘，对应(3s+1)(2s+1)
Kp = [0.5,2,5,10];                      % 设置多组比例系数变量

for m = 1:4                                 
    sys = feedback(Kp(m)*Gs,1);         % 构建单位负反馈闭环系统，feedback(G,H)表示G为前向通道，H为反馈通道
    step(sys);                          % 求解单位阶跃响应
    hold on;
end

仿真结论 ：随着 K p K_p Kp 取值增大，系统的动态响应速率显著提升，但超调量同步增大，调节时间随之延长；当 K p K_p Kp 增大至临界值后，闭环系统将由稳定状态逐步趋向不稳定。

比例控制的优势为抗干扰能力强、控制响应及时、过渡过程时间短，缺点为必然存在稳态误差。增大比例系数可提升系统开环增益，减小稳态误差与控制精度，但会降低系统的相对稳定性，甚至导致闭环失稳。因此在控制系统校正与设计中，比例控制一般不单独使用。

微分控制

微分控制的输出量与输入偏差的变化率成正比，工程中微分环节不单独使用 ，需与比例环节组合形成 PD 控制，其传递函数为：
G ( s ) = K p ( 1 + T d s ) G(s) = K_p(1+T_d s) G(s)=Kp(1+Tds)

固定比例系数，选取多组不同的微分时间常数，绘制系统的单位阶跃响应曲线，仿真代码如下：

matlab 复制代码 
Kp = 10;
Td = [0,0.4,1,4];
for m = 1:4
    G1 = tf([Kp*Td(m),Kp],[0,1]);            % 构建PD控制器传递函数，对应表达式 Kp(1+Td*s)
    sys = feedback(G1*Gs,1);                 % 构建PD控制闭环系统
    step(sys); hold on;
end

仿真结论 ：随着 T d T_d Td 取值增大，系统的超调量逐步减小，动态特性得到改善，稳定裕度提升。

自动控制系统在误差调节过程中出现振荡甚至失稳的原因：被控对象中存在大惯性或纯滞后环节，其误差抑制的调节动作始终滞后于误差的变化。仅引入比例环节仅能放大误差幅值，无法预判误差趋势；而微分项可基于误差变化率预判误差的发展趋势，使控制器提前将抑制误差的控制量收敛至零甚至负值，从而避免被控量的严重超调，有效优化系统动态特性。

微分环节的特性补充：仅对随时间动态变化的误差信号起作用，对恒定或缓变偏差无调节效果；对纯滞后环节无改善作用，且存在放大高频噪声信号的弊端。

积分控制

积分控制的输出量与输入偏差的时间积分成正比，本质为对误差的累积补偿，工程中积分环节需与比例环节组合形成 PI 控制，其传递函数为：
G ( s ) = K p ( 1 + 1 T i ⋅ s ) G(s) = K_p\left(1+\frac{1}{T_i \cdot s}\right) G(s)=Kp(1+Ti⋅s1)

固定比例系数，选取多组不同的积分时间常数，绘制系统的单位阶跃响应曲线，仿真代码如下：

matlab 复制代码 
Kp = 2;
Ti = [3,6,12,24];
for m = 1:4
    G1 = tf([Kp,Kp/Ti(m)],[1,0]);              % 构建PI控制器传递函数，对应表达式 Kp(1+1/(Ti*s))
    sys = feedback(G1*Gs,1);
    step(sys); hold on;
end

仿真结论 ：引入积分控制后，系统的稳态误差被完全消除，实现无静差调节；随着 T i T_i Ti 取值增大，积分作用减弱，系统进入稳态的过渡时间逐步延长。

积分环节的控制逻辑：积分输出随误差的时间累积而增大，即使偏差量微小，积分项也会随时间持续叠加，推动控制器输出增大，直至稳态误差归零。积分环节的弊端为降低系统的稳定裕度，使超调量增大、过渡时间延长，存在稳定性与准确性的权衡关系。

比例-积分-微分控制（PID 控制）

将比例、积分、微分三个环节进行线性组合，构成完整的 PID 控制器，其传递函数为：
G ( s ) = K p ( 1 + 1 T i ⋅ s + T d s ) G(s) = K_p\left(1+\frac{1}{T_i \cdot s}+T_d s\right) G(s)=Kp(1+Ti⋅s1+Tds)

选取适配的比例、积分、微分参数，绘制系统的单位阶跃响应曲线，仿真代码如下：

matlab 复制代码 
Kp = 100;                                % 设定比例系数
Ti = 2.2;                                % 设定积分时间常数
Td =7;                                   % 设定微分时间常数

G1 = tf([Kp*Td,Kp,Kp/Ti],[0,1,0]);       % 构建PID控制器传递函数
sys = feedback(G1*Gs,1);
step(sys);
hold on;

仿真结论：PID 控制综合了 PI 控制与 PD 控制的优势，通过积分环节消除稳态误差，通过微分环节抑制超调、加快响应，同时保留比例环节的快速反馈特性，是兼顾系统稳定性、快速性与准确性的最优组合控制方式。

MATLAB 可视化 PID 调节器

在新版本 MATLAB 软件中集成了专用的 PID 调节器工具箱，可实现控制器参数的可视化整定与优化，本仿真采用 MATLAB R2015a 版本，工具箱界面如下：

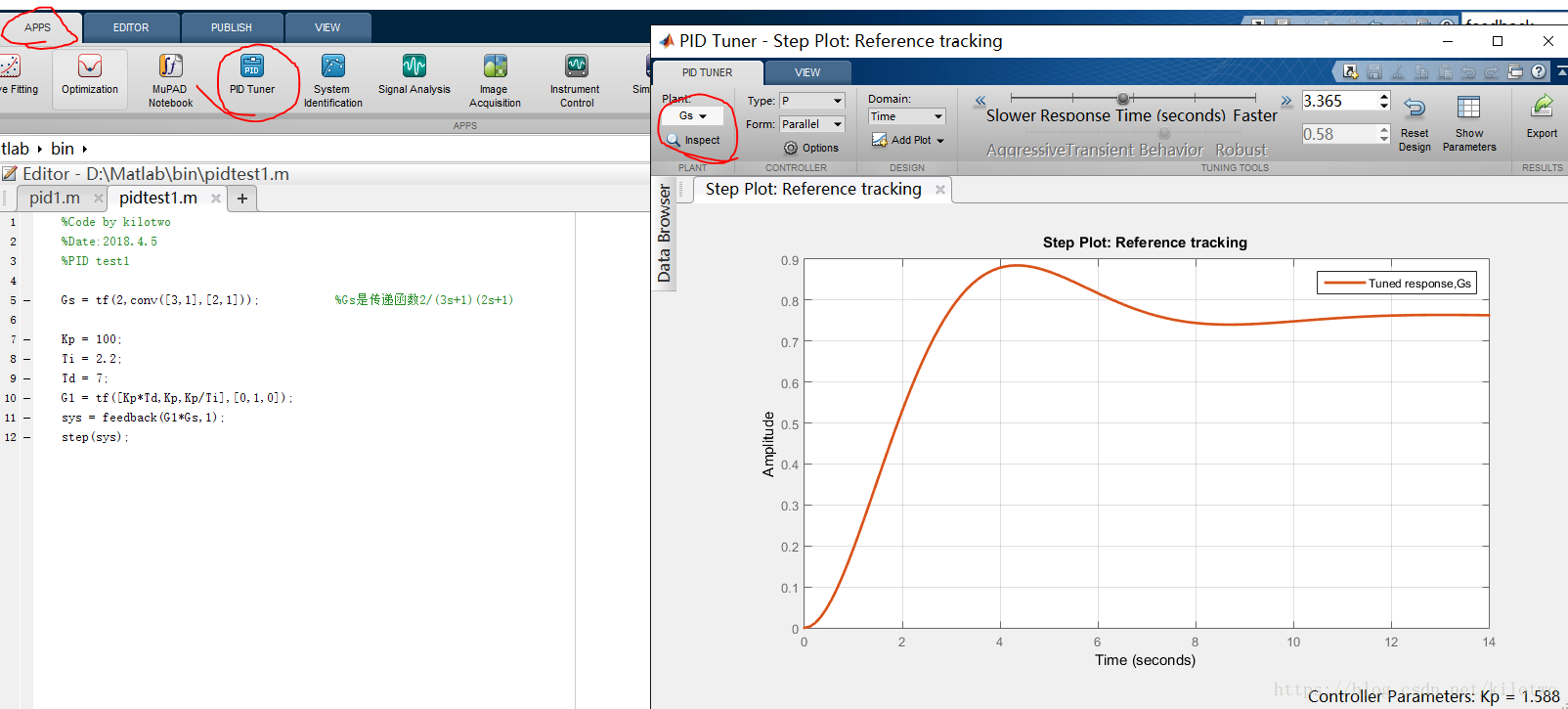
该工具箱的功能为：已知被控对象传递函数的前提下，对单位负反馈系统的 PID 参数进行整定，使系统单位阶跃响应满足预设性能指标，操作流程如下：

  1. 点击 Plant 栏的 Import 按钮，从 MATLAB 工作区导入被控对象的传递函数，支持多对象同时整定；
  2. 通过 Type 选项切换控制器类型，可选 P/I/PI/PD/PID/PDF/PIDF 等模式；
  3. 通过 Domain 选项选择整定域：时域整定可调节响应时间（response time）与暂态特性（transient behavior），频域整定可调节带宽（bandwidth）与相角裕度（phase margin）；
  4. 点击 show parameter 可查看控制器整定参数与响应曲线特征量（超调量、调节时间、稳态误差等）；
  5. 点击 Export 可将整定完成的 PID 参数导出至 MATLAB 工作区，供后续仿真调用。

曲线交互功能：点击响应曲线上任意点位，可实时显示该点对应的横、纵坐标数值。

总结

本文从理论推导与仿真验证两个维度，完成对连续系统 PID 控制算法的系统性分析；通过 MATLAB 实现了 PID 各环节的仿真验证，证明该软件可高效完成参数整定与性能分析。在工程实践前，通过仿真手段获取可靠的参数区间，能够大幅降低实际调试成本，提升开发效率。

对连续域 PID 算法的认知为基础，计算机控制系统为离散采样控制，需将连续域 PID 公式进行离散化处理，该部分内容将在后续章节中展开阐述。

PID 控制算法（二）------PID 算法离散化和增量式 PID 算法原理及 Matlab 实现

引言

前文完成对连续域 PID 控制算法的阐述，而计算机控制系统属于采样离散控制，控制器仅能依据采样时刻的偏差量完成控制量运算，无法直接应用连续域的 PID 公式。

因此需对连续 PID 算法做离散化处理：以累加运算近似替代积分运算，以向后差分近似替代微分运算，将连续的微分方程转化为离散的差分方程，得到数字 PID 控制算法。

离散化近似基础

当控制系统的采样周期 T T T 选取足够小时，可对连续域的积分与微分运算做如下数值近似，该近似的精度随采样周期减小而提升：

式中参数定义：

  • T T T ------ 系统采样周期
  • k k k ------ 采样序号， k = 0 , 1 , 2 ... k=0,1,2\dots k=0,1,2...

基于上述数值近似方法，可推导得到两种典型的数字 PID 控制算法：位置式 PID 算法与增量式 PID 算法。

位置式 PID 算法

由连续域 PID 公式结合离散化近似，可直接推导得到位置式 PID 算法的离散表达式：

算法特性 ：位置式 PID 的输出量 u ( k ) u(k) u(k) 与采样时刻 k k k 之前的所有偏差信号 e ( i ) e(i) e(i) 均相关，控制器需对历史偏差做持续累加运算，不仅运算量较大，还需占用较多存储单元，且输出量为被控对象的绝对控制量，一旦运算出错易造成系统大幅波动，工程中应用受限，因此实际控制系统中多采用增量式 PID 算法。

增量式 PID 算法

针对位置式 PID 算法的运算冗余与控制风险问题，对其做增量化改进：控制器的输出量不再是被控对象的绝对控制量，而是相邻采样时刻的控制量增量 Δ u ( k ) \Delta u(k) Δu(k)。增量式 PID 的推导为对位置式输出做差分运算，其表达式为：

{ Δ U o ( n ) = K P { [ ε ( n ) − ε ( n − 1 ) ] + T T I ε ( n ) + T D T [ ε ( n ) − 2 ε ( n − 1 ) + ε ( n − 2 ) ] } U ( k ) = Δ u ( k ) + U ( k − 1 ) \begin{cases} \Delta U_o(n) = K_P \left\{ \left[ \varepsilon(n) - \varepsilon(n-1) \right] + \frac{T}{T_I} \varepsilon(n) + \frac{T_D}{T} \left[ \varepsilon(n) - 2\varepsilon(n-1) + \varepsilon(n-2) \right] \right\} \\ U(k) = \Delta u(k) + U(k-1) \end{cases} {ΔUo(n)=KP{[ε(n)−ε(n−1)]+TITε(n)+TTD[ε(n)−2ε(n−1)+ε(n−2)]}U(k)=Δu(k)+U(k−1)

或

{ Δ U o ( n ) = K P [ ε ( n ) − ε ( n − 1 ) ] + K I ε ( n ) + K D [ ε ( n ) − 2 ε ( n − 1 ) + ε ( n − 2 ) ] U ( k ) = Δ u ( k ) + U ( k − 1 ) \begin{cases} \Delta U_o(n) = K_P \left[ \varepsilon(n) - \varepsilon(n-1) \right] + K_I \varepsilon(n) + K_D \left[ \varepsilon(n) - 2\varepsilon(n-1) + \varepsilon(n-2) \right] \\ U(k) = \Delta u(k) + U(k-1) \end{cases} {ΔUo(n)=KP[ε(n)−ε(n−1)]+KIε(n)+KD[ε(n)−2ε(n−1)+ε(n−2)]U(k)=Δu(k)+U(k−1)

注： U ( k ) U(k) U(k) 是 PID 控制器的输出

算法优势：增量式 PID 的输出仅与最近 3 个采样时刻的偏差量相关，无需累加历史偏差，运算量大幅降低；输出为控制量增量，即使运算出错也仅造成小幅波动，系统鲁棒性显著提升；可便捷实现手动/自动无扰切换，是工业控制与嵌入式系统中最常用的 PID 实现形式。

Matlab 仿真实现（增量式 PID）

仿真实现流程

  1. 对被控对象传递函数 G ( s ) G(s) G(s) 做离散化处理，通过 Z Z Z 变换得到离散域传递函数 G ( z ) G(z) G(z)；
  2. 将 G ( z ) G(z) G(z) 的分子、分母多项式同除 z z z 的最高次幂，转化为标准差分方程形式；
  3. 依据 Z Z Z 变换的位移定理 Z [ e ( t − k t ) ] = z − k E ( z ) \mathcal{Z}[e(t-kt)]=z^{-k}E(z) Z[e(t−kt)]=z−kE(z)，完成 Z Z Z 域到离散时域的逆变换，得到被控对象的差分方程；
  4. 编写增量式 PID 控制算法，结合被控对象差分方程完成闭环仿真。

仿真细节与逻辑说明均体现在代码注释中，完整仿真代码如下：

matlab 复制代码 
% 被控对象传递函数 G(s)=50/(0.125s^2+7s)
% 增量式 PID 控制仿真：输入为单位阶跃/正弦信号，采样周期 1ms，控制器输出限幅[-3,3]
% 输出曲线包含：系统响应曲线、误差变化曲线

ts=0.001;                 % 设定采样周期
sys=tf(50,[0.125,7, 0]);  % 定义被控对象连续传递函数
dsys=c2d(sys,ts,'z');     % 连续系统离散化，Z变换得到离散传递函数 G(z)=Y(z)/U(z)
[num,den]=tfdata(dsys,'v');% 提取离散传递函数的分子、分母多项式系数

% 初始化变量：存储前两时刻的输入、输出、误差
u_1=0.0;  
u_2=0.0;  
y_1=0.0;  
y_2=0.0;  
x=[0,0,0]';  
error_1=0;  
error_2=0;  

for k=1:1:1000  
    time(k)=k*ts;                   % 采样时间轴
    S=1;
    if S==1                         % 模式1：单位阶跃输入
        kp=6.5;ki=0.1;kd=1;         % PID 参数初始化    
        rin(k)=1;                   % 阶跃输入信号   
    elseif S==2                     % 模式2：正弦输入信号
        kp=10;ki=0.1;kd=15;             
        rin(k)=0.5*sin(2*pi*k*ts);    % 正弦输入信号      
    end 

    du(k)=kp*x(1)+kd*x(2)+ki*x(3);      % 增量式PID运算：计算控制量增量
    u(k)=u_1+du(k);                     % 当前控制量 = 前一时刻控制量 + 增量值
    
    % 控制器输出限幅，防止执行机构饱和
    if u(k)>=3         
       u(k)=3;  
    end  
    if u(k)<=-3  
       u(k)=-3;  
    end  

    % 被控对象差分方程实现：离散系统输出计算
    yout(k)=-den(2)*y_1-den(3)*y_2+num(2)*u_1+num(3)*u_2;          
    error(k)=rin(k)-yout(k);                                       % 计算当前采样时刻偏差
    
    % 变量迭代更新：保存历史值供下一周期运算
    u_2=u_1;                                                      
    u_1=u(k);                                                      
    y_2=y_1;                                                      
    y_1=yout(k);                                                   

    % 增量式PID偏差项更新
    x(1)=error(k)-error_1;                                         % 比例项偏差增量
    x(2)=error(k)-2*error_1+error_2;                               % 微分项偏差增量
    x(3)=error(k);                                                 % 积分项偏差值
    error_2=error_1;                                               
    error_1=error(k);                                               
end 

% 绘制仿真曲线
figure(1);  
plot(time,rin,'b',time,yout,'r');                        % 输入信号与系统输出曲线
xlabel('time(s)'),ylabel('rin,yout');   
figure(2);  
plot(time,error,'r')                                     % 系统误差变化曲线
xlabel('time(s)');ylabel('error');

仿真效果（PID 参数整定后）

PID 参数工程整定流程

数字 PID 参数的整定遵循「先比例、后积分、最后微分」的原则，为工程通用的试凑法，流程如下：

  1. 整定比例系数 K p K_p Kp

    关闭积分与微分环节（令 T i → ∞ T_i\to\infty Ti→∞、 T d = 0 T_d=0 Td=0），仅保留纯比例控制。将系统输入设定为额定输出的 60 % ∼ 70 % 60\% \sim70\% 60%∼70%， K p K_p Kp 从 0 逐步增大，直至系统响应出现持续振荡；再反向减小 K p K_p Kp 至振荡消失，取此时值的 60 % ∼ 70 % 60\% \sim70\% 60%∼70% 作为比例系数的整定初值。

  2. 整定积分时间常数 T i T_i Ti

    保持已整定的 K p K_p Kp 不变，设定较大的 T i T_i Ti 初值并逐步减小，直至系统响应出现振荡；再反向增大 T i T_i Ti 至振荡消失，取此时值的 150 % ∼ 180 % 150\% \sim180\% 150%∼180% 作为积分时间常数的整定初值。

  3. 整定微分时间常数 T d T_d Td

    微分环节一般可先置零，此时 PID 退化为 PI 控制，可满足多数系统需求；若需引入微分环节，按比例系数的整定逻辑，取系统不振荡时 T d T_d Td 值的 30 % 30\% 30% 作为初值。

  4. 系统联调与参数微调

    完成上述三步后，对 K p 、 T i 、 T d K_p、T_i、T_d Kp、Ti、Td 做小范围迭代微调，直至系统响应的超调量、调节时间、稳态误差均满足预设性能指标，完成空载与带载的全工况验证。

基于MATLAB/Simulink平台可实现可视化图形化仿真建模，该方式无需编写程序代码，仅通过模块拖拽、链路搭建，完成PID控制器参数整定与被控对象传递函数的参数配置，即可快速搭建完整的PID闭环控制系统，建模效率高、操作便捷，可直观完成控制系统的仿真分析。

仿真模型结构

参数说明

需关注Filter coefficient参数，其作用为前向滤波，本仿真中该参数取值为1。

改进型微分项设计

本仿真中微分项采用如下形式：
微分项 = D ⋅ N 1 + N ⋅ 1 s \text{微分项} = D \cdot \frac{N}{1 + N \cdot \frac{1}{s}} 微分项=D⋅1+N⋅s1N

当 N N N 取值足够大时，该微分项可退化为常规形式 D s D s Ds。

微分项滤波的必要性

  1. 常规微分项的缺陷 ：高频噪声会对输出信号造成显著干扰；当误差信号的变化率较微弱时，若微分系数 D D D 过大，易产生过量校正量，导致系统振荡加剧而非抑制。
  2. 滤波器的作用：滤除微分项中的高频校正分量，优化微分环节的控制效果，属于微分项的改进设计。

仿真运行后，双击示波器模块即可查看系统响应曲线与误差曲线：

结论

  1. 基于 MATLAB 的 PID 参数整定与仿真，具备高效、便捷、直观的特点，可有效规避传统试凑法的反复调试，大幅缩短开发周期。
  2. 比例系数 K p K_p Kp 增大，系统响应速率加快，稳态误差减小，但超调量增大，稳定裕度降低； K p K_p Kp 过小则系统响应迟缓，调节效率低下。
  3. 积分时间常数 T i T_i Ti 增大，积分作用减弱，系统超调量减小、稳定性提升，但稳态误差的消除速率变慢，过渡时间延长； T i T_i Ti 过小则积分作用过强，易引发系统振荡。
  4. 微分时间常数 T d T_d Td 增大，系统超调量减小、稳定裕度提升、响应速率加快； T d T_d Td 过大则微分作用过强，易放大高频噪声，导致调节时间延长； T d T_d Td 过小则微分校正不足，无法有效抑制超调。
  5. PID 参数的整定本质为对稳定性、快速性、准确性三者的权衡与优化，需充分理解各参数的独立作用与耦合关系，结合系统特性完成适配性整定。

相关 Matlab 代码和 Simulink 仿真文件下载地址：
https://download.csdn.net/download/kilotwo/10329949

PID 控制算法（三）------增量式与位置式 PID 算法的 C 语言实现与电机控制经验总结

前文完成对 PID 算法离散化与增量式 PID 原理的推导，及 MATLAB 仿真验证，形成了理论认知。

本章将基于嵌入式系统完成 PID 算法的 C 语言工程实现，并结合直流电机的速度/位置闭环控制项目，总结 PID 算法的工程应用经验。

1 增量式 PID 算法 C 语言工程实现

以下为通用型增量式 PID 算法的标准 C 语言实现代码，代码具备良好的可读性与移植性，适用于 51/STM32/STM8 等主流嵌入式控制器，是电机控制、运动控制等场景的经典实现形式：

c 复制代码 
typedef struct PID
{
    int SetPoint;    // 控制目标值 DesiredValue
    long SumError;   // 误差累计值（位置式备用）
    double Proportion; // 比例系数 Kp
    double Integral;    // 积分系数 Ki
    double Derivative;  // 微分系数 Kd
    int LastError;   // 前一时刻偏差 e[k-1]
    int PrevError;   // 前两时刻偏差 e[k-2]
} PID;

static PID sPID;
static PID *sptr = &sPID;

/**************************************************************************
函数功能：PID 结构体参数初始化
入口参数：无
返回值  ：无
**************************************************************************/
void IncPIDInit(void)
{
    sptr->SumError  = 0;
    sptr->LastError = 0;  // 初始化偏差值e[k-1]
    sptr->PrevError = 0;  // 初始化偏差值e[k-2]
    sptr->Proportion= 0;  // 初始化比例系数
    sptr->Integral  = 0;  // 初始化积分系数
    sptr->Derivative= 0;  // 初始化微分系数
    sptr->SetPoint  = 0;  // 初始化目标值
}

/**************************************************************************
函数功能：增量式 PID 计算函数
入口参数：NextPoint - 当前采样值（反馈量）
返回值  ：iIncpid  - 控制量增量值
**************************************************************************/
int IncPIDCalc(int NextPoint)
{
    register int iError, iIncpid;  // 定义当前偏差与增量输出
    iError = sptr->SetPoint - NextPoint;  // 计算当前偏差 e[k] = 目标值 - 反馈值

    // 增量式PID公式：Δu(k) = Kp[e(k)-e(k-1)] + Ki*e(k) + Kd[e(k)-2e(k-1)+e(k-2)]
    iIncpid = sptr->Proportion * iError        // 比例项 Kp*e[k]
            - sptr->Integral * sptr->LastError  // 积分项 Ki*e[k-1]
            + sptr->Derivative * sptr->PrevError;// 微分项 Kd*e[k-2]

    // 偏差迭代更新：为下一采样周期做准备
    sptr->PrevError = sptr->LastError;
    sptr->LastError = iError;

    return(iIncpid);  // 返回控制量增量
}

2 PID 参数整定工程口诀

工程实践中总结的 PID 参数整定口诀，是现场调试的重要参考依据，该口诀覆盖了参数整定的逻辑与规律，适用于绝大多数闭环控制系统的参数试凑，需结合实际调试过程理解与运用：

复制代码 
参数整定找最佳， 从小到大顺序查。
先是比例后积分， 最后再把微分加。
曲线振荡很频繁， 比例度盘要放大。
曲线漂浮绕大弯， 比例度盘往小扳。
曲线偏离回复慢， 积分时间往下降。
曲线波动周期长， 积分时间再加长。
曲线振荡频率快， 先把微分降下来。
动差大来波动慢， 微分时间应加长。
理想曲线两个波， 前高后低四比一。
一看二调多分析， 调节质量不会低。

口诀说明：该整定规律是工程经验的高度凝练，对初学者而言偏抽象，其内涵需在实际调试中逐步体会，逻辑与前文的理论整定流程一致。

3 直流电机闭环控制项目原理

理论认知需结合工程实践落地，本节以直流电机的速度/位置闭环控制为应用场景，阐述 PID 算法的工程化应用，硬件选型参考平衡小车主流方案，原理简洁且具备通用性。

3.1 直流电机基础特性

直流电机的驱动逻辑为：电枢两端施加正向电压时电机正转，施加反向电压时电机反转；电机的输出转速与电枢两端的平均电压呈正相关（本质由电枢电流决定），可通过 PWM 脉宽调制技术调节电枢电压，实现电机转速的无级调速。

3.2 减速器的作用

常规直流电机的空载转速可达每分钟数千转甚至上万转，输出转矩较小，无法直接驱动负载。减速器 为精密机械传动部件，作用为降速增矩：通过齿轮啮合降低输出转速，同时按传动比放大输出转矩，使电机的可控性与负载能力显著提升。

减速器的分类：按传动级数分为单级/多级减速器；按传动类型分为齿轮减速器、蜗杆减速器、行星齿轮减速器，直流电机控制中以行星齿轮减速器应用最广。

3.3 电机驱动芯片 TB6612FNG

单片机的 IO 口输出电流微弱，无法直接驱动大电流感性负载的直流电机，需通过功率驱动芯片完成功率放大。本项目选用 TB6612FNG 作为电机驱动核心，其为东芝半导体推出的双通道直流电机驱动芯片，特性如下：

  • 采用大电流 MOSFET-H 桥拓扑，单通道持续输出电流可达 1.2A，峰值电流 3.2A；
  • 无需外接散热片与续流二极管，外围电路仅需滤波电容，硬件设计简洁，体积小巧；
  • PWM 输入频率最高支持 100 kHz，可有效抑制电机低速运行时的机械抖动与电磁噪声；
  • 性能优于传统 L298N 驱动芯片，无明显热损耗，是嵌入式电机控制的优选方案。

3.4 编码器（速度/位置反馈元件）

编码器是将角位移/角速度转换为电脉冲信号的旋转式传感器，是闭环控制的反馈元件，可实现电机转速与位置的精准测量。

  • 按输出类型 分：增量式编码器、绝对式编码器；本项目选用增量式霍尔编码器，成本低、可靠性高，满足电机闭环控制需求。
  • 按检测原理分：光电编码器、霍尔编码器、磁编码器；霍尔编码器无光学磨损，抗干扰能力强，更适用于工业与车载场景。

编码器特性：具备 A、B 两相正交脉冲输出，可通过脉冲计数实现转速测量，通过两相脉冲的相位差判别电机转向；编码器内置上拉电阻，脉冲信号可直接接入单片机 IO 口，无需额外硬件上拉。

单片机采集编码器数据的方法：

  1. 带硬件编码器接口的控制器（如 STM32）：直接配置定时器为编码器模式，硬件自动完成脉冲计数与转向判别，精度高、无软件开销；
  2. 无硬件编码器接口的控制器（如 51）：将 A 相信号接入外部中断引脚，通过跳变沿触发中断，在中断服务函数中读取 B 相电平，判定电机转向并完成脉冲计数。

4 电机速度闭环控制（增量式 PI 实现）

4.1 控制原理

速度闭环控制的逻辑：通过编码器采集单位时间内的脉冲数，换算为电机实际转速；将实际转速与目标转速做差值得到速度偏差，通过增量式 PI 算法运算得到控制增量，最终通过 PWM 脉宽调制调节电机电枢电压，使实际转速跟踪目标转速，实现无静差的速度稳定控制。

工程设计要点 ：本项目的速度控制周期设定为 20 m s 20\ ms 20 ms（常规为 5 ms ∼ 10 ms 5\ \text{ms} \sim 10\ \text{ms} 5 ms∼10 ms），因 USB 供电的电机转速较低，适当延长采样周期可提升编码器的脉冲采集精度，降低测速误差。

主控芯片选用 STM32F103C8T6，通过定时器编码器模式采集脉冲数，PID 运算在定时中断中完成，输出 PWM 波驱动 TB6612FNG，实现闭环控制。

4.2 速度闭环控制代码

电机速度控制中，微分环节易放大测速噪声，因此工程中普遍采用增量式 PI 控制，即可满足无静差调速需求，又能保证系统稳定，代码如下：

c 复制代码 
/**************************************************************************
函数功能：增量式 PI 速度控制器（电机专用）
入口参数：Encoder - 编码器采样值（单位时间脉冲数），Target - 目标转速（脉冲数）
返回  值：电机PWM占空比增量
公式参考：ΔPWM = Kp[e(k)-e(k-1)] + Ki*e(k)
**************************************************************************/
int Incremental_PI (int Encoder,int Target)
{   
    float Kp=20,Ki=30;   
    static int Bias,Pwm,Last_bias;         // 定义偏差、PWM输出、历史偏差
    Bias=Encoder-Target;                // 计算转速偏差：测量值 - 目标值
    Pwm+=Kp*(Bias-Last_bias)+Ki*Bias;   // 增量式PI运算
    Last_bias=Bias;                     // 保存历史偏差，供下一周期使用
    return Pwm;                         // 返回PI调节后的PWM值
}

代码说明：该函数严格遵循增量式 PI 公式编写， K p 、 K i K_p、K_i Kp、Ki 为整定后的参数，直接在函数内赋值，逻辑简洁，易于调试与修改。

4.3 定时中断控制逻辑

速度闭环的控制逻辑在定时器中断中执行，本项目设定 10 ms为控制周期，中断内完成「采样-运算-输出」的闭环流程，代码如下：

c 复制代码 
int Target_velocity=50;  // 设定目标转速：50个脉冲/10ms
int TIM3_IRQHandler(void)  
{    
    if(TIM3->SR&0X0001)  // 10ms定时中断触发
    {   
        TIM3->SR&=~(1<<0);               // 清除中断标志位         
        Encoder=Read_Encoder(2);         // 读取编码器脉冲数（M法测速）
        Led_Flash(100);                  // LED闪烁，指示系统正常运行   
        Moto1=Incremental_PI(Encoder,Target_velocity);  // PI速度调节
        Xianfu_Pwm();                    // PWM输出限幅，防止超量程
        Set_Pwm(Moto1);                  // 将PWM值写入寄存器，驱动电机  
    }           
    return 0;    
}

4.4 辅助功能代码（完整工程必备）

包含 PWM 限幅、电机转向控制、绝对值运算等辅助函数，为电机控制的标准配套代码，确保系统稳定运行：

c 复制代码 
/**************************************************************************
函数功能：PWM赋值与电机转向控制
入口参数：moto1 - PWM占空比值
返回  值：无
**************************************************************************/
void Set_Pwm(int moto1)
{
    if(moto1>0)         AIN2=1, AIN1=0;  // 正转
    else                AIN2=0, AIN1=1;  // 反转
    PWMA=myabs(moto1);                   // 赋值PWM占空比（取绝对值）
}

/**************************************************************************
函数功能：PWM输出限幅函数，防止执行机构饱和
入口参数：无
返回  值：无
**************************************************************************/
void Xianfu_Pwm(void)
{   
    int Amplitude=7100;    // PWM最大幅值7200，限幅7100预留余量
    if(Moto1<-Amplitude) Moto1=-Amplitude;  
    if(Moto1>Amplitude)  Moto1=Amplitude;   
}

/**************************************************************************
函数功能：整型绝对值运算函数
入口参数：int a - 待运算数
返回  值：unsigned int - 绝对值结果
**************************************************************************/
int myabs(int a)
{          
    int temp;
    if(a<0)  temp=-a;  
    else temp=a;
    return temp;
}

4.5 主函数初始化代码

完成系统时钟、PWM、编码器、定时器中断的初始化，程序进入死循环等待中断触发，是嵌入式程序的标准结构：

c 复制代码 
int main(void)
{ 
    Stm32_Clock_Init(9);            // 系统时钟初始化
    MiniBalance_PWM_Init(7199,0);   // PWM初始化：10KHz，避免电机低频啸叫
    Encoder_Init_TIM2();            // 编码器接口初始化
    Timer3_Init(99,7199);           // 定时器初始化：10ms进入一次中断
    while(1);                       // 主循环等待中断
}

5 电机位置闭环控制（位置式 PID 实现）

5.1 控制原理

位置闭环控制的逻辑：通过编码器的脉冲累加值，计算电机的实际转角/位置；将实际位置与目标位置做差值得到位置偏差，通过位置式 PID 算法运算得到控制量，调节电机转向与转速，使电机精准到达目标位置，实现无静差的位置定位控制。

位置闭环对控制精度要求更高，因此引入微分环节构成完整的 PID 控制，可有效抑制位置超调，提升定位精度与稳定性。

5.2 位置闭环控制代码

位置式 PID 算法的工程实现代码，适用于电机的精准定位控制，公式严格遵循离散化位置式 PID 表达式，代码如下：

c 复制代码 
/**************************************************************************
函数功能：位置式 PID 位置控制器（电机专用）
入口参数：Encoder - 编码器位置累加值，Target - 目标位置值
返回  值：电机PWM占空比
公式参考：PWM = Kp*e(k) + Ki*Σe(k) + Kd[e(k)-e(k-1)]
**************************************************************************/
int Position_PID (int Encoder,int Target)
{   
    float Position_KP=80,Position_KI=0.1,Position_KD=500;
    static float Bias,Pwm,Integral_bias,Last_Bias;
    Bias=Encoder-Target;                                  // 计算位置偏差
    Integral_bias+=Bias;                                    // 偏差积分累积
    Pwm=Position_KP*Bias+Position_KI*Integral_bias+Position_KD*(Bias-Last_Bias);
    Last_Bias=Bias;                                       // 保存历史偏差
    return Pwm;                                           // 返回位置PID输出
}

5.3 位置闭环中断控制代码

与速度闭环逻辑一致，位置控制在 10 ms 定时中断中完成，仅需将速度 PI 函数替换为位置 PID 函数即可，代码如下：

c 复制代码 
int Target_position=11000;    // 设定目标位置：11000个脉冲
int TIM3_IRQHandler(void)  
{    
    if(TIM3->SR&0X0001)  // 10ms定时中断触发
    {   
        TIM3->SR&=~(1<<0);                                       // 清除中断标志位       
        Encoder=Read_Encoder(2);                                  // 读取编码器位置累加值
        Led_Flash(100);                                           // LED闪烁指示运行状态  
        Moto1=Position_PID(Encoder,Target_position);              // 位置PID调节
        Xianfu_Pwm();                                             // PWM限幅
        Set_Pwm(Moto1);                                          // PWM输出驱动电机  
    }           
    return 0;    
}

6 PID 参数整定的工程原则

PID 参数整定的目标是使控制系统同时满足稳定性、快速性、准确性三大性能指标，对应的量化评估参数为：

  • 稳定性：以最大超调量、振荡次数为评估指标，超调量越小、振荡次数越少，系统稳定性越好；
  • 快速性：以上升时间、调节时间为评估指标，时间越短，系统的动态响应越快；
  • 准确性：以稳态误差为评估指标，稳态误差越小，系统的控制精度越高。

工程整定的原则

不同控制系统对性能指标的优先级要求不同，参数整定需针对性优化：

  1. 平衡车、倒立摆等快速响应类系统 ：优先保证快速性，允许适当超调，需增大 K p K_p Kp、减小 T i T_i Ti，微分环节按需配置；
  2. 门窗开合、精密定位等高精度类系统 ：优先保证准确性与稳定性，需减小 K p K_p Kp、增大 T d T_d Td，积分环节消除静差；
  3. 电机调速等通用类系统：三者均衡优化，多采用 PI 控制，避免微分环节放大噪声。

控制系统的调试难度，主要取决于被控对象的转动惯量 与响应速度要求：转动惯量越小、响应要求越低，PID 参数的鲁棒性越强，整定越容易；反之则参数敏感度高，需精细化调试。

7 总结

嵌入式控制系统的调试过程中，硬件特性会受环境因素影响产生漂移，导致控制效果波动。想要整定出适配全工况的最优参数，需在不同环境、不同负载下完成多组测试，通过数据积累与分析得到综合最优解。图形化仿真工具可快速直观地验证参数有效性，是工程调试的重要辅助手段。

对于平衡车、四旋翼飞行器等复杂多变量系统，除 PID 算法外，还需对传感器数据做滤波、限幅、权重分配等预处理，这些进阶内容将在后续文章中进一步总结。

增量式 PID 速度调节代码已上传，位置式代码可参考修改实现，下载地址：
https://download.csdn.net/download/kilotwo/10350922

线性控制算法

1. 适用范围

适用于满足叠加性与齐次性的线性系统，且系统模型已知。

2. 核心算法类型

包含比例（P）、比例-积分（PI）、比例-微分（PD）、比例-积分-微分（PID）四类控制算法。

3. 基本原理

线性控制算法以系统偏差信号 e ( t ) = r ( t ) − y ( t ) e(t) = r(t) - y(t) e(t)=r(t)−y(t)（ r ( t ) r(t) r(t) 为参考输入， y ( t ) y(t) y(t) 为系统输出）为核心输入，通过不同控制环节的组合构建控制律，具体表达式如下：

  • P控制 ：仅含比例环节，输出与偏差呈线性比例
    u ( t ) = K p e ( t ) u(t) = K_p e(t) u(t)=Kpe(t)

    其中 K p K_p Kp 为比例系数。

  • PI控制 ：融合比例与积分环节，积分环节用于消除稳态误差
    u ( t ) = K p [ e ( t ) + 1 T i ∫ 0 t e ( τ ) d τ ] u(t) = K_p \left[ e(t) + \frac{1}{T_i} \int_{0}^{t} e(\tau) d\tau \right] u(t)=Kp[e(t)+Ti1∫0te(τ)dτ]

    其中 T i T_i Ti 为积分时间常数。

  • PD控制 ：融合比例与微分环节，微分环节用于预判偏差变化趋势
    u ( t ) = K p [ e ( t ) + T d d e ( t ) d t ] u(t) = K_p \left[ e(t) + T_d \frac{de(t)}{dt} \right] u(t)=Kp[e(t)+Tddtde(t)]

    其中 T d T_d Td 为微分时间常数。

  • PID控制 ：综合比例、积分、微分三环节，兼顾各环节优势
    u ( t ) = K p [ e ( t ) + 1 T i ∫ 0 t e ( τ ) d τ + T d d e ( t ) d t ] u(t) = K_p \left[ e(t) + \frac{1}{T_i} \int_{0}^{t} e(\tau) d\tau + T_d \frac{de(t)}{dt} \right] u(t)=Kp[e(t)+Ti1∫0te(τ)dτ+Tddtde(t)]

4. 符号定义与物理意义

（1）符号说明
符号 全称 含义
r ( t ) r(t) r(t) Reference input 参考输入（目标值）
y ( t ) y(t) y(t) System output 系统输出（实际值）
e ( t ) e(t) e(t) Error signal 误差信号（目标值与实际值的差值）
（2）误差信号的物理意义
  • e ( t ) > 0 e(t) > 0 e(t)>0：系统输出低于参考输入，控制器需增大输出以缩小偏差；
  • e ( t ) < 0 e(t) < 0 e(t)<0：系统输出高于参考输入，控制器需减小输出；
  • e ( t ) = 0 e(t) = 0 e(t)=0：系统达到期望状态，控制器维持当前输出。

5. 适用场景

  • P控制：简单系统的粗调（如电阻加热温度初步控制），对稳态误差、动态响应要求不高的场景；
  • PI控制：需无静差调节的线性系统（如电机转速稳定控制、电网电压调节）；
  • PD控制：对动态特性要求高、需抑制超调的系统（如机床进给轴位置控制、精密仪器定位）；
  • PID控制：工业领域通用场景（如化工反应釜温度控制、风机变频调速），需同时兼顾稳定性、快速性与准确性的线性系统。

6. 特性分析

（1）共性优势

结构简洁、物理意义明确，工程实现难度低，可通过模拟电路或简单数字逻辑实现。

（2）各环节特性
  • P控制：响应速度快，但存在固有稳态误差；比例系数过大会导致系统振荡；
  • PI控制：可完全消除稳态误差，但积分环节存在滞后性，可能降低动态响应速度；积分时间常数过小易引发超调；
  • PD控制：可抑制超调、提升稳定裕度，但对高频噪声敏感；微分时间常数过大会放大噪声干扰；
  • PID控制：综合三环节优势，可平衡系统稳定性、快速性与准确性，但在强非线性、参数时变或扰动显著的场景中鲁棒性不足，需结合自适应或补偿机制优化。

via:

热门推荐
01GitHub 镜像站点022025 Telegram 最新免费社工库机器人（LetsTG可[特殊字符]）搭建指南（含 Python 脚本）032025年大语言模型技术全景报告04Linux下V2Ray安装配置指南05UV安装并设置国内源06安娜的档案(Anna’s Archive) 镜像网站/国内最新可访问入口（持续更新）07Claude Code Skills 实用使用手册08BongoCat - 跨平台键盘猫动画工具09Labelme从安装到标注：零基础完整指南10AI 规范驱动开发“三剑客”深度对比：Spec-Kit、Kiro 与 OpenSpec 实战指南