隐马尔可夫链模型 基础概念
主要参考：
书籍：《统计学习方法（第二版）》
隐马尔可夫链模型 Hidden Markov Model (HMM)
定义：隐马尔可夫链模型是关于时序的概率模型，描述由一个隐藏的马尔可夫链随机生成不可观测的状态随机序列，再由各个状态生成一个观测从而产生观测随机序列的过程。
直观理解 - 掷骰子
为了更好的理解，我们举 掷骰子 的例子进行直观的讲解。
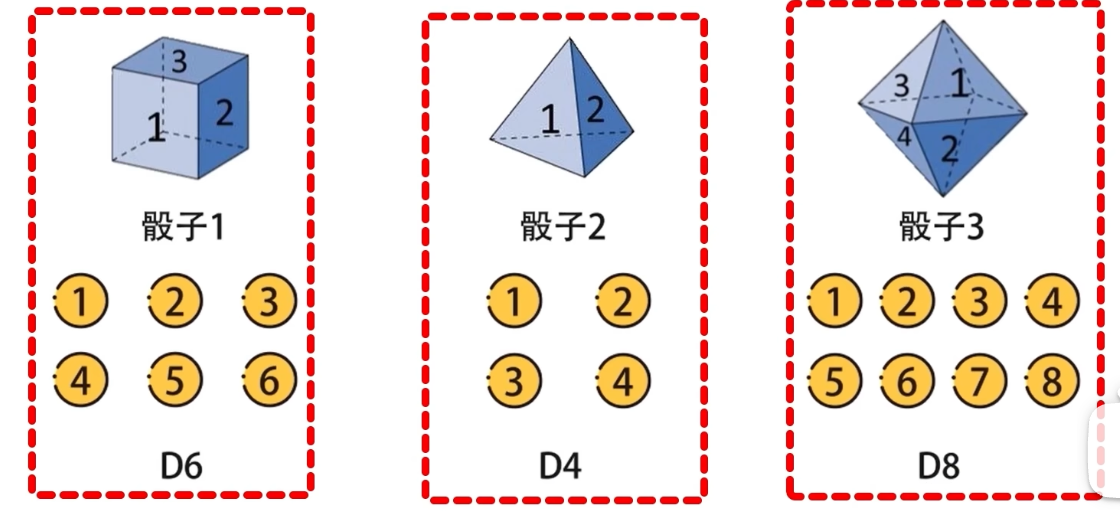我们一共有3个骰子，分别是正方体（6个面 为D6）,正四面体（四个面 为D4），正八面体（8个面 为D8）
同时，我们 蒙着眼睛 从这三个骰子中进行随机选择（假设各个骰子的手感无差别），进而结果可能是1-8中的任意一个。
我们进行 重复 随机的选择骰子 ，不断的抛掷，然后可以得到一个随机的 可见状态练：
注意：这个可见状态链就是我们抛掷骰子的结果，我们因为是无法看到骰子，所以我们并不知道选择的是哪个骰子进行抛掷的。
进而我们每次抛掷的骰子都是隐藏的，我们并不知道。
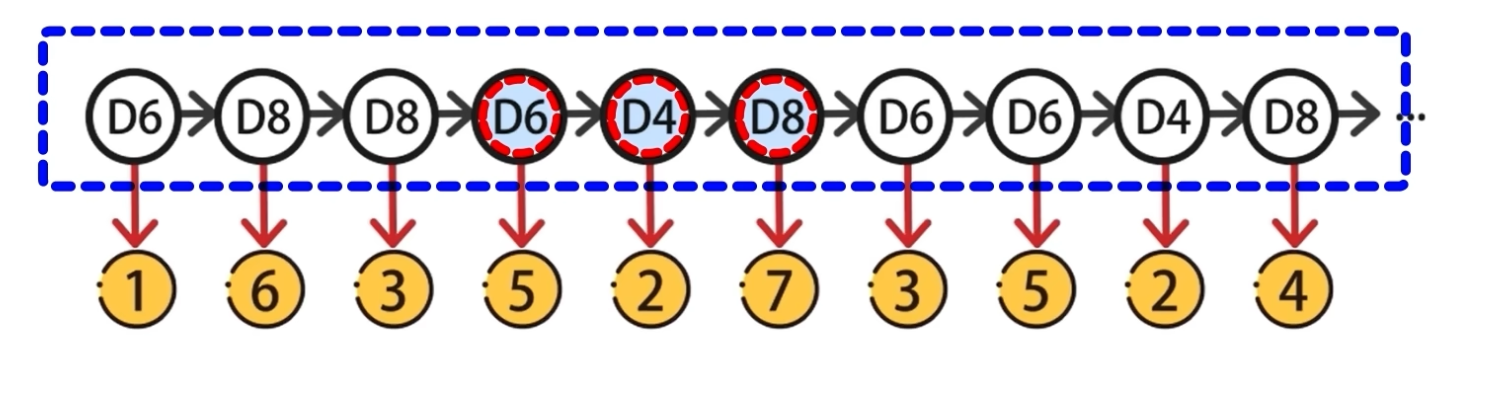
就如上图所示，D6-D8-D8-...... 是我们看不到的抛掷顺序的骰子编号序列。我们称为 隐含状态链。
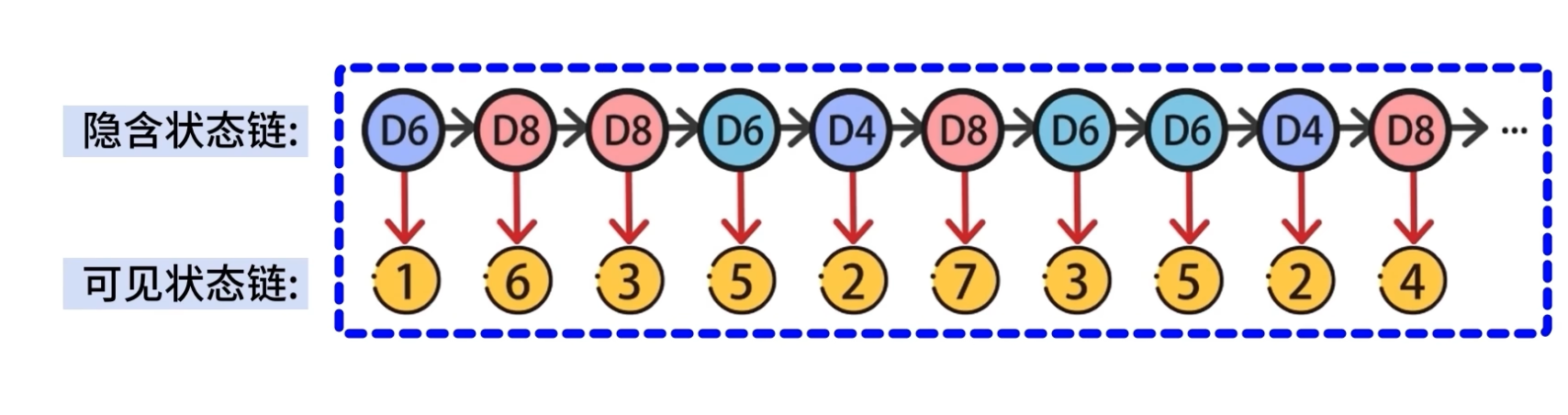
隐马尔可夫模型 = 可见状态链 + 隐含状态链
回归到定义中，可以表示为：
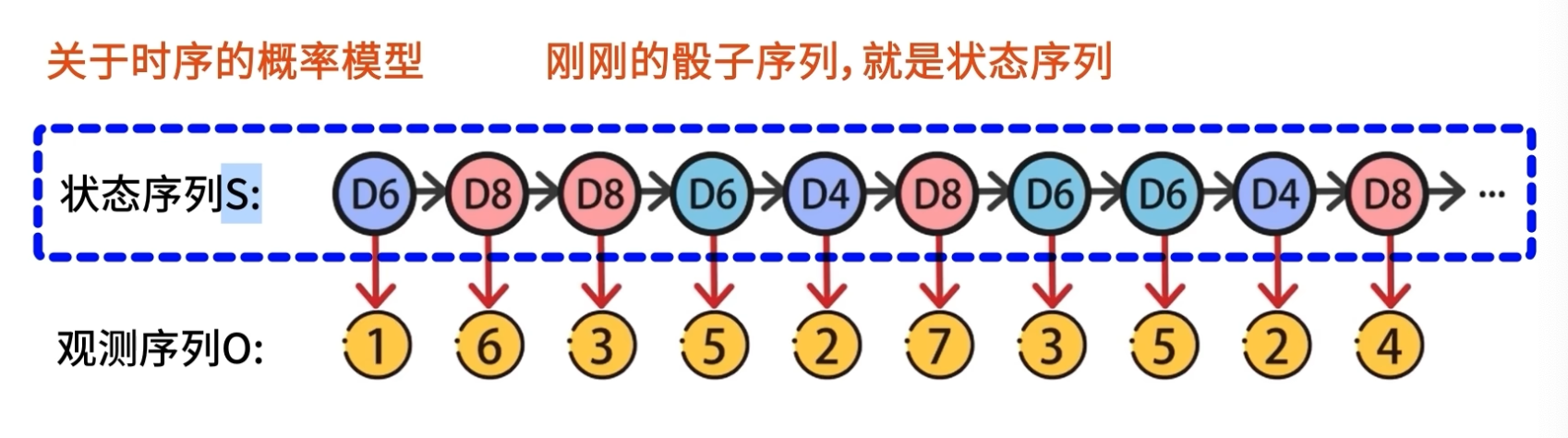
刚才的骰子序列就是状态序列
骰子掷出的数字就是数字序列
若有t个时刻，t可以表示为第几次掷骰子。
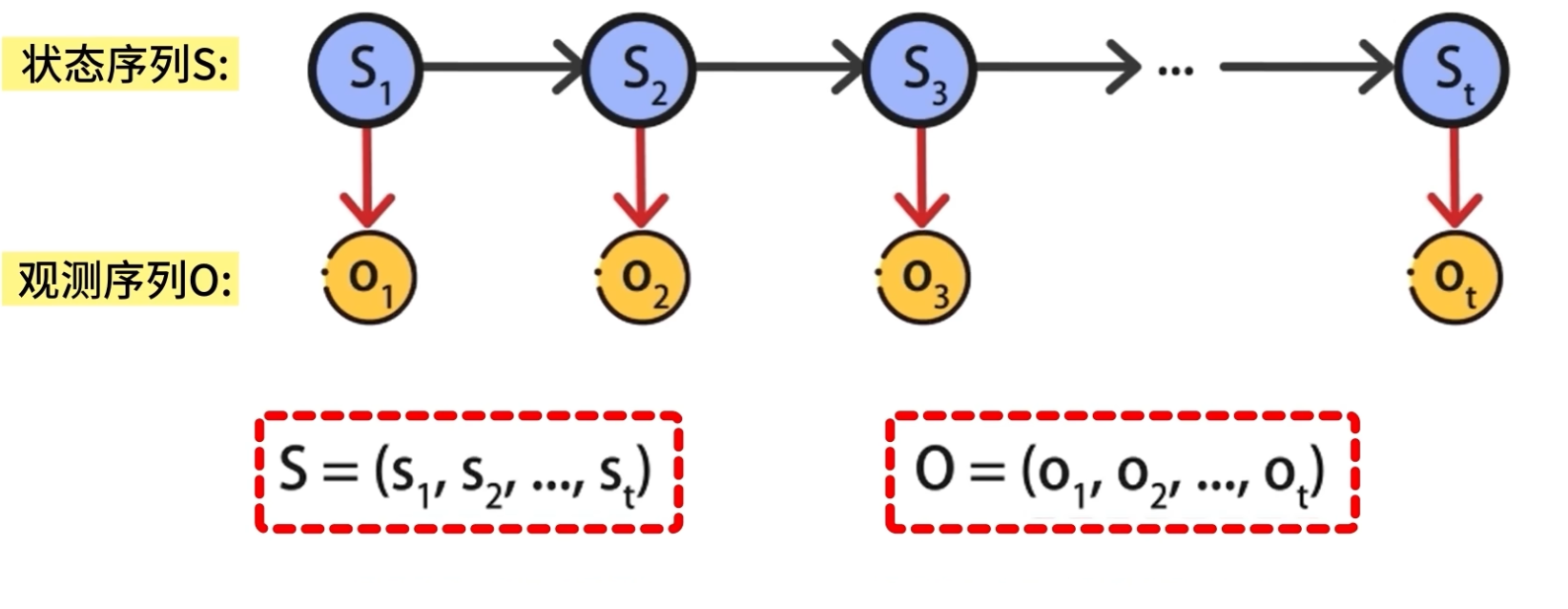
状态序列是隐藏的，无法被观测到，因此状态变量是一个隐变量。
各个隐含状态之间会进行转换，存在着对应的转换概率。
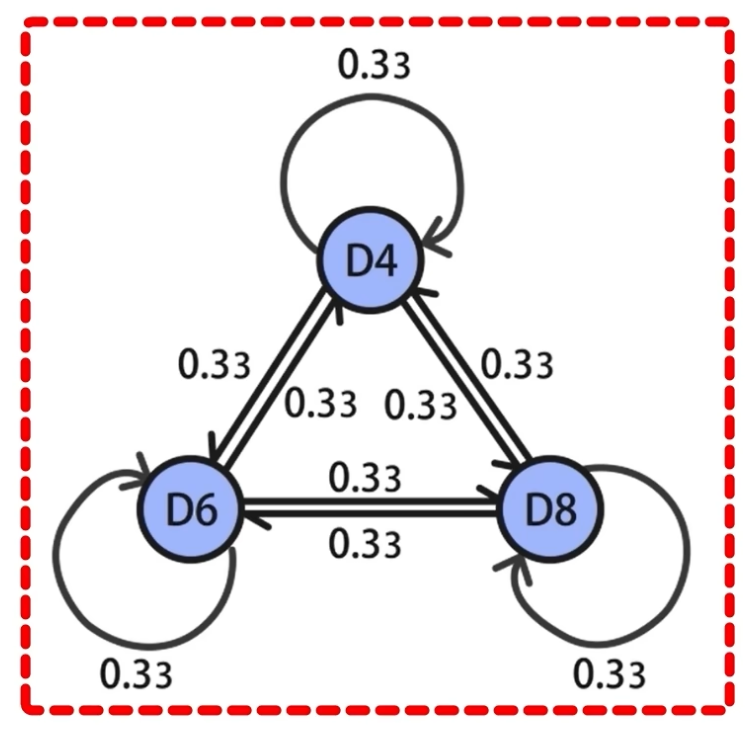
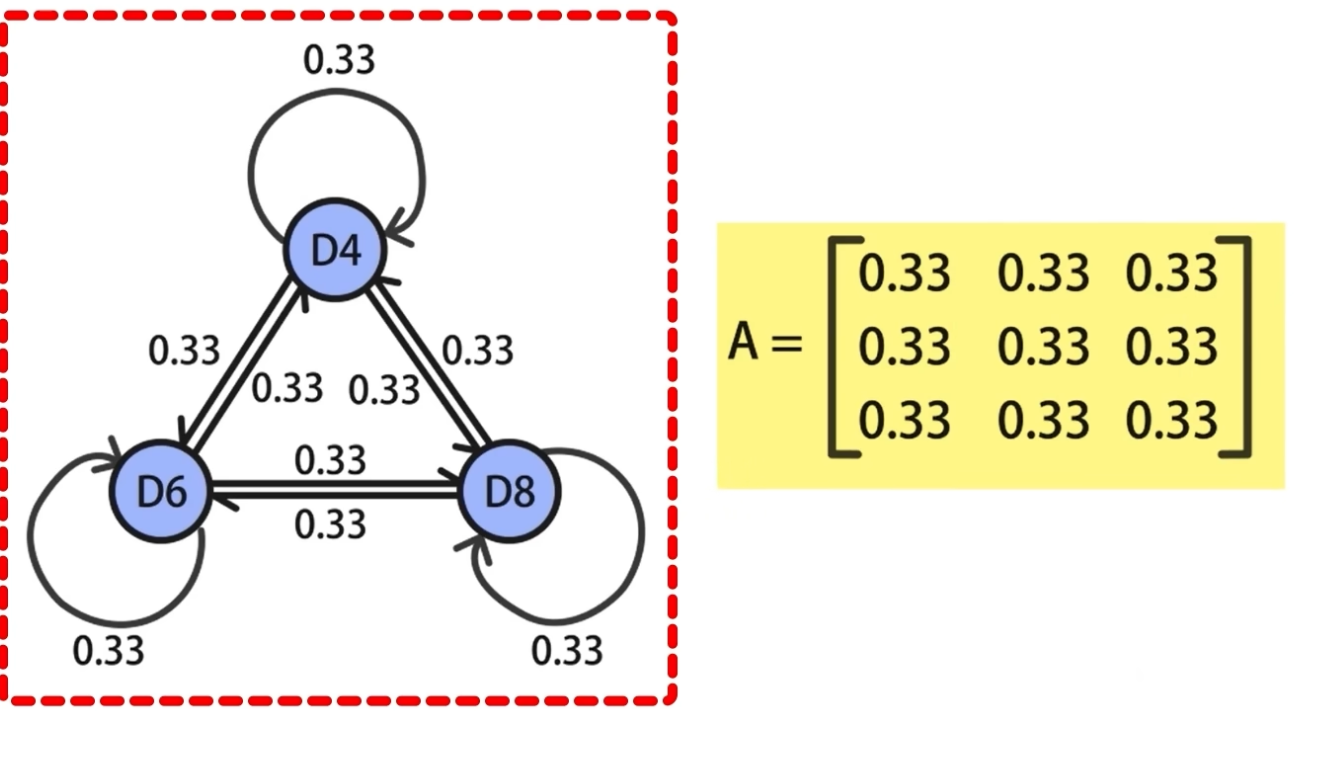
在 掷骰子的时候因为我们是可重复随机挑选的骰子，那么每个骰子选中的概率都是1/3。
同时隐含状态会输出可见状态，隐含状态与可见状态之间有一个输出概率，不同的隐含状态到可见状态的概率可能不同。
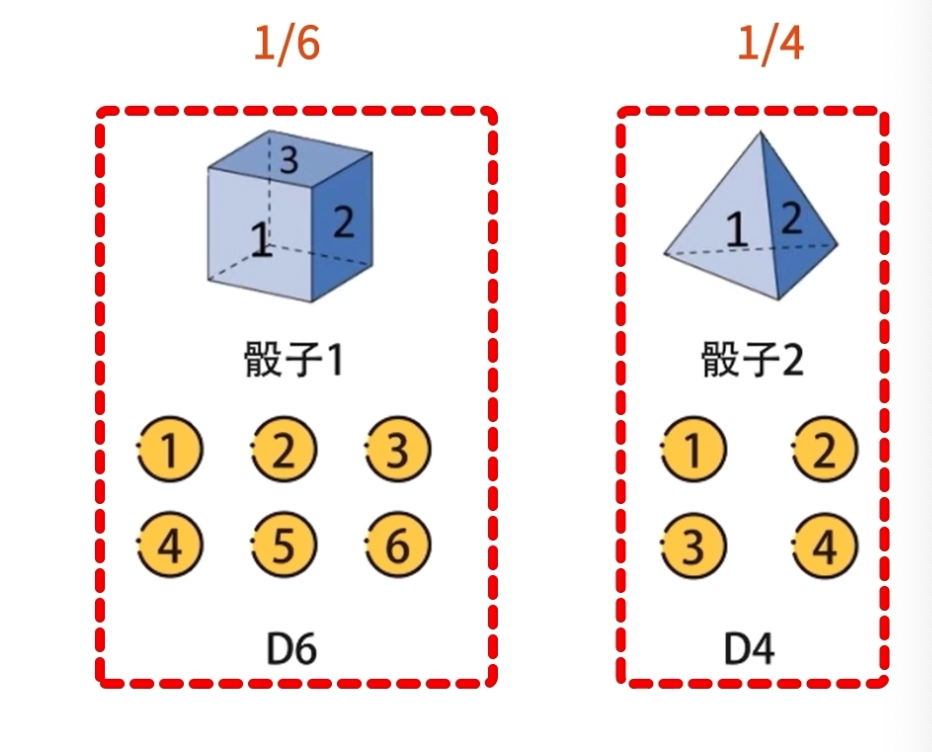
例如不同骰子中的有不同的面数会导致选中的概率不同
正六面体，选中一个数字的概率是1/6，而正四面体选中一个数字的概率是1/4。
隐马尔可夫链模型的数学表示
基础表示：
隐含状态 Q
观测结果 V
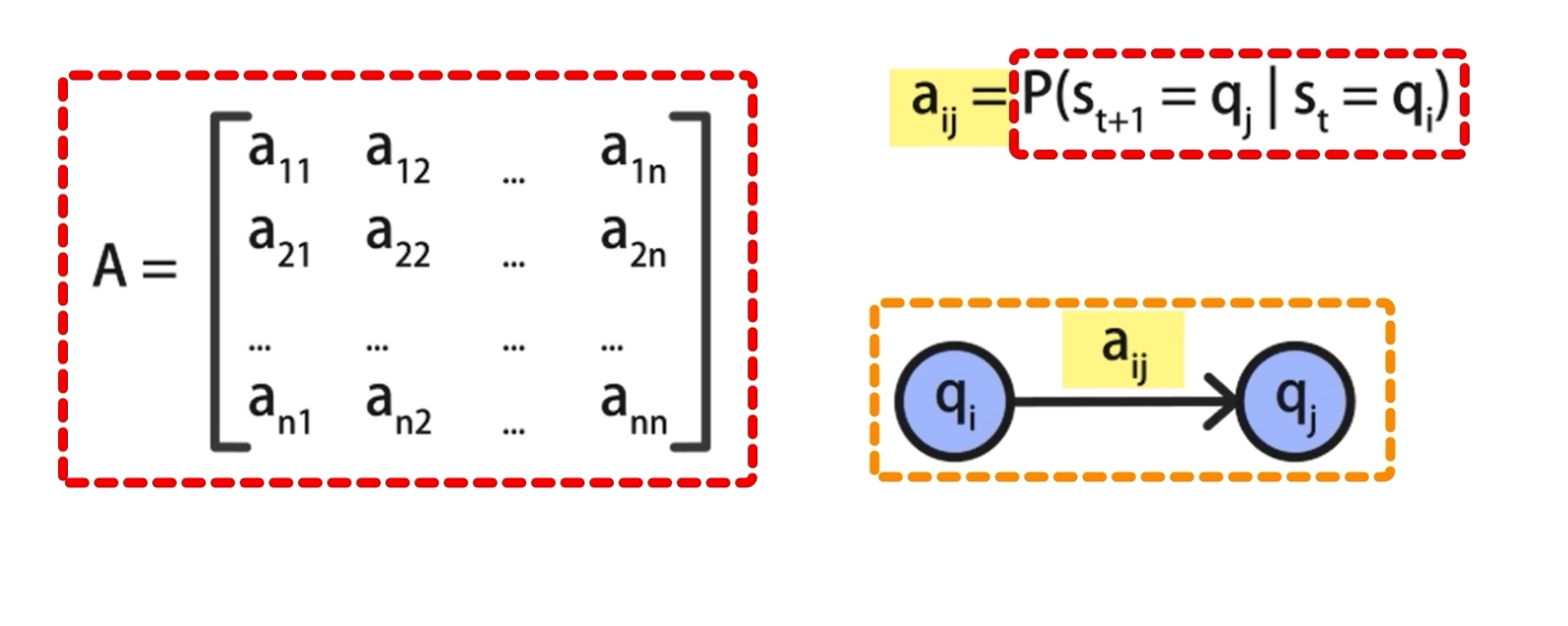
状态转移概率矩阵 A
观测概率矩阵 B
初始状态概率向量 $$\pi$$
隐含状态 Q && 观测结果 V
隐含状态Q包含了q1到qn的n种状态，观测结果V包含了v1到vm的m种可能的结果。
在掷骰子中 q1表示的是六面体，q2表示的是四面体，q3表示的是八面体。
v1到v8分别表示的是数字1到8。
状态转移概率矩阵 A
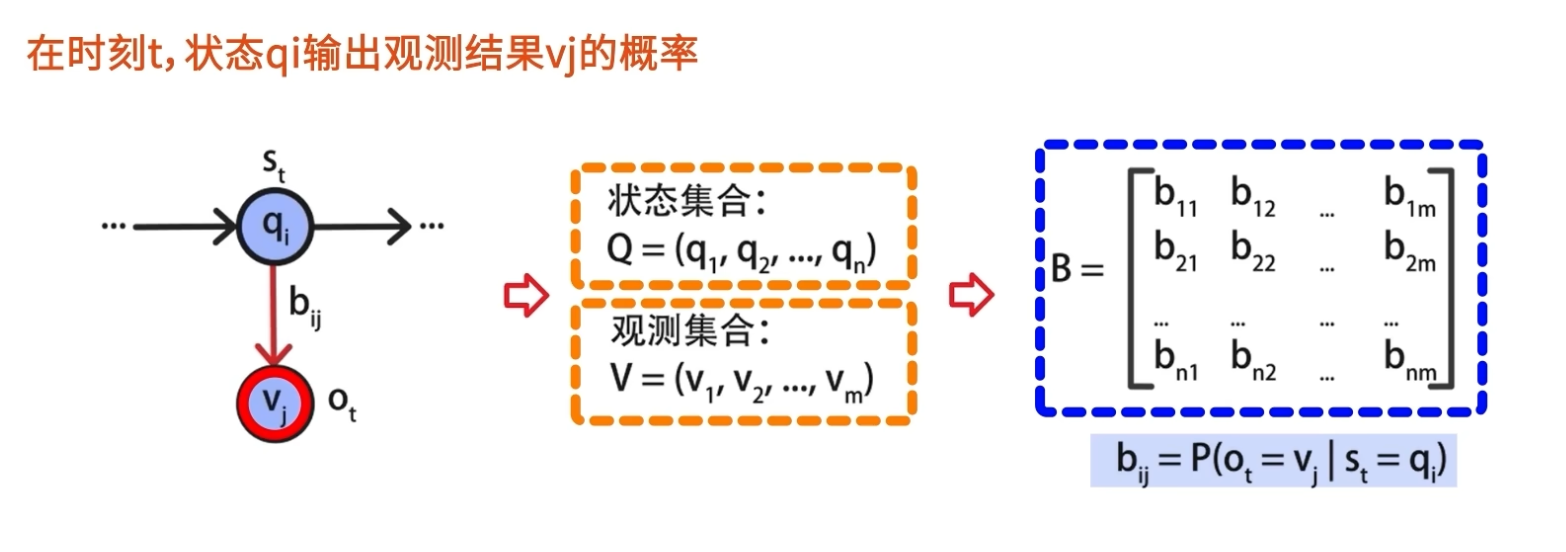
\[a_{ij}$$表示从状态q_i转移到状态q_j的概率。 $$a_{ij}$$ = 在s_t等于q_i的条件下s_{t+1}等于q_j的概率 \]
例如：三个骰子，选择任意一个骰子的概率都是1/3，进而 状态转移概率矩阵A 如下：
观测概率矩阵 B
由于每一个状态q都可以输出一个观测结果v，因此B是一个 n*m 的矩阵。
例如；在掷骰子的时候，根据三个骰子的输出，可以得到一个3乘8的概率矩阵。
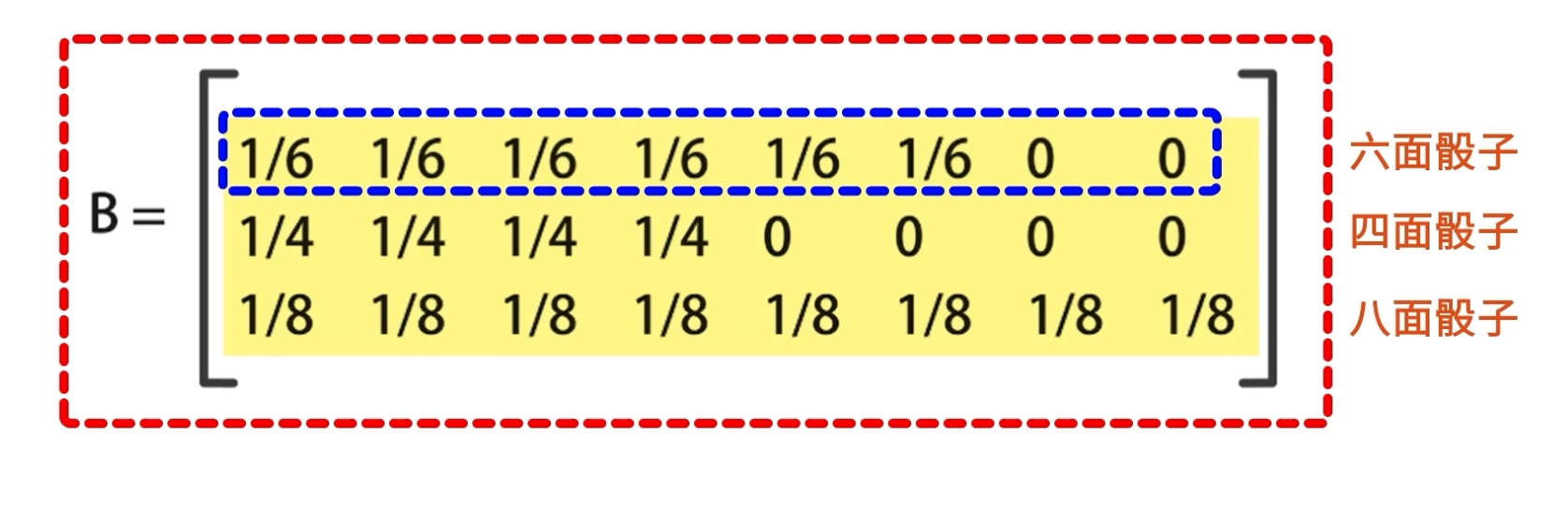
第一行是表示六面骰子的输出概率
第二行是四面骰子的输出概率
第三行是八面骰子的输出概率
初始状态概率向量 $$\pi$$
例如，掷骰子的时候三种骰子的初始概率都是1/3（约为0.33）。
总结
\(\pi\)和A确定了隐藏的马尔可夫链，如何生存不可观测的状态序列s
B确定了如何从隐藏状态产生观测序列o
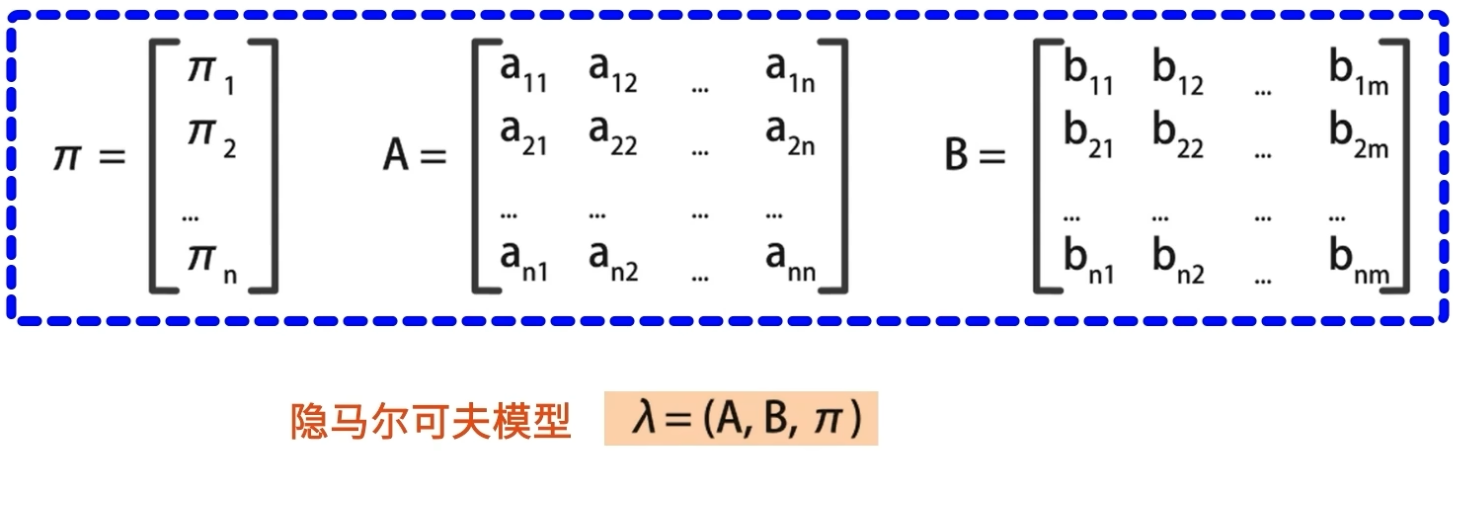
隐马尔可夫模型由A B \(\pi\) 共同决定。