【SimpleITK】B-Spline 配准中的多分辨率陷阱与验证

前言

最近在研究 SimpleITK 的非刚性配准（B-Spline Registration），跟着官方教程跑代码，结果遇到了一系列让人摸不着头脑的现象：

1. Python 代码里明明没有 for 循环，它是怎么跑完 3 层金字塔的？

2. 配准明明成功了，为什么损失函数（Metric）曲线最后反而升高了？

3. 最离谱的是：用更高级的"多分辨率动态网格"策略，结果反而比"傻瓜式固定网格"差得十万八千里（TRE 误差爆炸）？

经过一番深度排查和计算，终于破案了。这篇文章将带你一层层剥开 SimpleITK 抽象 API 的外衣，并揭示一个隐藏在小学数学里的"致命陷阱"。

---

一、 那个"看不见"的循环：SimpleITK 的封装艺术

在配置多分辨率配准时，核心代码只有这几行：

Python

# 设定 3 层金字塔，缩放因子分别为 1倍、2倍、4倍
registration_method.SetInitialTransformAsBSpline(
    initial_transform, inPlace=True, scaleFactors=[1, 2, 4]
)
registration_method.SetShrinkFactorsPerLevel(shrinkFactors=[4, 2, 1])

疑问： 代码里完全没有 for 循环，它是怎么实现"先跑第1层，把结果传给第2层，再跑第3层"的？

解析：

这正是 SimpleITK（以及底层 ITK）的设计哲学------声明式编程。

• 我们写的 Python 代码只是在**"填菜单"**（设置参数），并没有真正执行。

• 真正的 for 循环和逻辑控制被封装在 C++ 底层。

• 当你调用 registration_method.Execute() 时，底层的 C++ 引擎会读取你的 scaleFactors 清单，自动完成以下"接力赛"：

  1. Level 1：用稀疏网格跑配准 -> 得到参数。

  2. Upsample：C++ 自动把网格分裂变密（自动计算新坐标）。

  3. Level 2：继承上一层的参数作为起点，继续优化。

  4. ...以此类推。

感悟： 不要试图在 Python 层去找循环，把参数设好，剩下的交给 C++ 黑盒。

---

二、 怎么才算配准好了？Dice 系数详解

配准完之后，我们怎么评价效果？除了看重叠图，最硬的指标就是 Dice 系数 (Dice Coefficient)。

1. 什么是 Dice？

简单来说，就是**"重叠度打分"**。

• 1.0 (满分)：两个肺部 Mask 完美重合。

• 0.0 (零分)：完全不沾边。

2. 代码实现

SimpleITK 提供了现成的工具类，注意看这段代码的细节：

Python

# 关键点：对 Label 变形时，必须用 NearestNeighbor (最近邻插值)
transformed_labels = sitk.Resample(
    masks[moving], fixed_image, tx, 
    sitk.sitkNearestNeighbor, 0.0, masks[moving].GetPixelID()
)

# 计算 Dice
label_overlap = sitk.LabelOverlapMeasuresImageFilter()
label_overlap.Execute(ground_truth, transformed_labels)
print(f"Dice: {label_overlap.GetDiceCoefficient()}")

避坑指南：

在 Resample 标签图时，千万不要用线性插值（Linear） ！否则整数标签（如 1=肺, 3=骨头）会被平均成小数（1+3=2），凭空变出不存在的组织。必须用 sitkNearestNeighbor。

---

三、 诡异现象：为什么 Metric 不降反升？

在查看配准过程的 Metric（损失函数）曲线时，我发现了一个奇怪的现象：

现象： 在第 200 次迭代（进入最后阶段）时，Metric 值突然从几千飙升到了几万，而且一直维持在高位，看起来比一开始还差。

原因分析：这是"考试难度"变了。

这对应了代码中的 SetShrinkFactorsPerLevel(shrinkFactors=[4, 2, 1])：

• 前两阶段：图像被缩小了（模糊了）。像素之间的灰度差异很小，MeanSquares（均方差）天然就低。

• 最后阶段 ：突然切换回原始分辨率（高清原图）。高清图里包含了所有的血管纹理、噪点和伪影，像素方差剧增。

结论： Metric 升高是因为它在计算高清图的差异，而不是配准变差了。不同分辨率层级之间的 Metric 绝对值没有可比性。

---

四、 终极破案：为什么更高级的方法反而"爆炸"了？

这是本文最核心的部分。

1. 案发现场

我对比了两组实验结果：

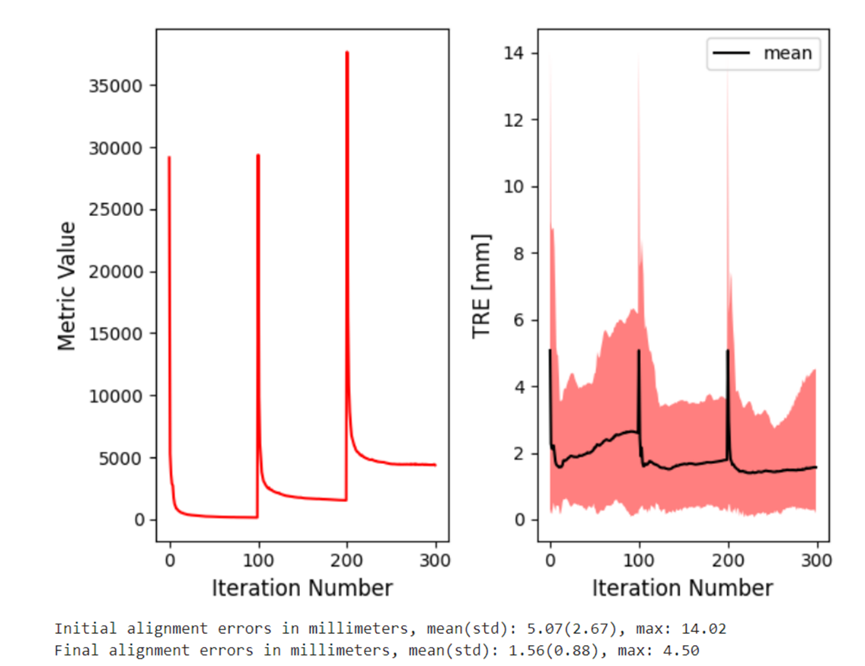
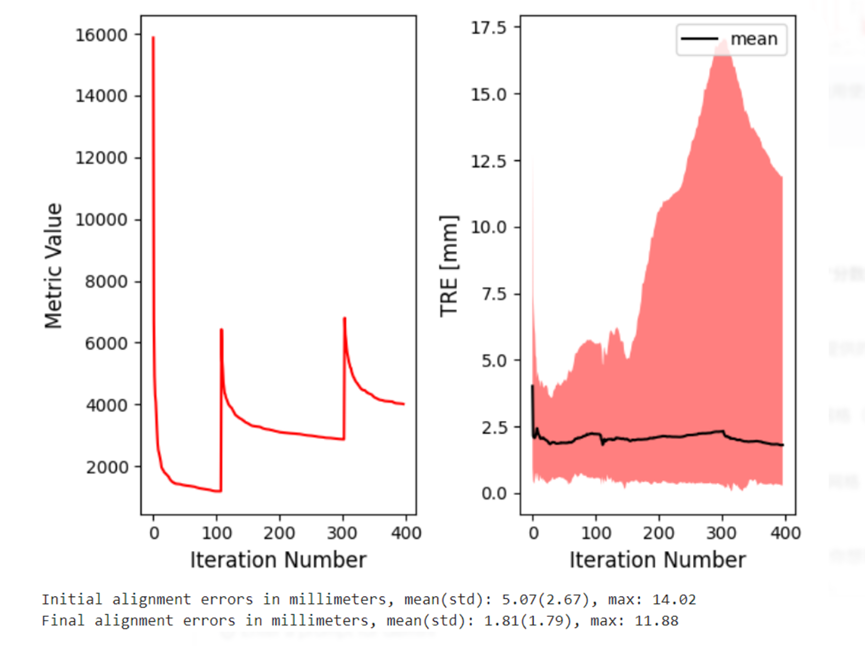
• 左图（Baseline）：使用固定网格（间距 50mm），网格大小从头到尾不变。

  • 结果：TRE（真实误差）很低，方差很小，效果稳健。

• 右图（Advanced）：使用多分辨率网格（动态加密），最后阶段理论上应该更精细。

  • 结果 ：TRE 直接爆炸，红色阴影（误差范围）巨大。过拟合了！

2. 为什么会过拟合？

• 左图 ：网格一直很稀疏（粗）。就像用大刷子刷墙，想抠细节也抠不出来，"由于分辨率低而被迫正则化"，反而不容易出事。

• 右图：最后阶段网格变密了。配合激进的优化器（LBFGS2），为了强行匹配高清图里的噪点，把网格扭曲成了麻花（Topology Breaking），导致解剖结构错乱。

3. 数学实锤：被"四舍五入"骗了！

我原本以为："右图先除以4，最后再乘以4，最后一层的网格密度应该和左图一样啊？"

大错特错！让我们算一笔账：

假设图像尺寸对应 50mm 间距大概需要 10个 格子。

• 左图（老实人算法）：

  直接计算：10 个控制点。

  N_{left} = 10

• 右图（多分辨率算法）：

  1. 先做除法（制造种子）：10 / 4 = 2.5。

     • 注意：程序里有 int() 取整！变成了 3。

  2. 再做乘法（最终层级）：3 \\times 4 = 12。

     N_{right} = 12

惊人发现：

10 vs 12。在三维空间里，控制点数量是立方的关系：

• 左图参数量：10\^3 = 1000

• 右图参数量：12\^3 = 1728

真相大白：

由于整数取整的误差，右图最终的网格密度比左图高了将近一倍！

参数多了一倍 + 没有加正则化惩罚项 + 激进的优化器 = 必然的过拟合与结果爆炸。

---

五、 总结

这次踩坑让我明白了 SimpleITK 配准的三个真理：

1. API 虽抽象，逻辑在心中：理解 C++ 底层的多分辨率接力机制，才能看懂参数。

2. Metric 只是参考：跨分辨率比较 Metric 毫无意义，要相信 Dice 和 TRE。

3. 小心"整形"陷阱 ：在多分辨率策略中，int(N/4)*4 永远不等于 N。这微小的差别，可能就是模型过拟合的罪魁祸首。

解决建议： 如果想用多分辨率网格，务必加上 BSplineTransformRegularization（正则化惩罚项），给你的优化器装上刹车！

---