在模长和幅角可自由变换的极坐标平面内3点结构有3个
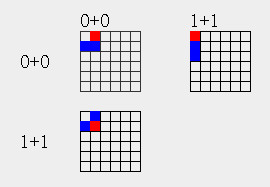
4点结构有6个
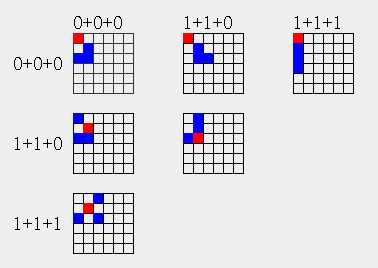
计算3+1
4((0+0|0+0)+1)=(1+1+0|1+1+0) + (0+0+0|1+1+0) + (0+0+0|0+0+0) + (1+1+0|0+0+0)
3((0+0|1+1)+1)=(0+0+0|1+1+1) + (1+1+0|1+1+0) + (0+0+0|1+1+0)
3((1+1|0+0)+1)=(1+1+0|1+1+0) + (1+1+0|0+0+0) + (1+1+1|0+0+0)
结构(0+0|0+0)+1可以得到4个4点结构。位置对应关系为
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| | | | | | | | | | | | | | | | 和 | | |
| 1 | 1 | 0 | | | 0 | 1 | 1 | | | 0 | 0 | 0 | | | 1 | 2 | 1 |
| 1 | 1 | | | | 0 | 1 | | | | 1 | 1 | | | | 2 | 3 | |
| 0 | | | | | 0 | | | | | 1 | | | | | 1 | | |
结果对称性很强
5点结构有15个
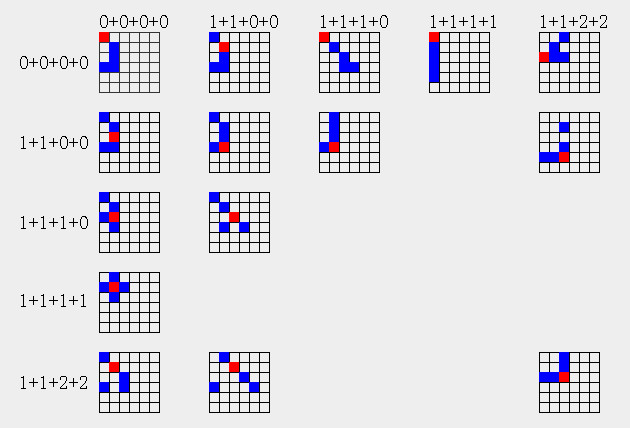
计算4+1
4((0+0+0|0+0+0)+1)=(0+0+0+0||0+0+0+0) + (1+1+0+0||0+0+0+0) + (0+0+0+0||1+1+0+0) + (1+1+0+0||1+1+0+0)
6((0+0+0|1+1+0)+1)=(1+1+0+0||1+1+2+2) + (0+0+0+0||1+1+0+0) + (1+1+0+0||1+1+0+0) + (0+0+0+0||1+1+1+0) + (0+0+0+0||1+1+2+2) + (1+1+0+0||1+1+1+0)
3((0+0+0|1+1+1)+1)=(0+0+0+0||1+1+1+1) + (1+1+0+0||1+1+1+0) + (0+0+0+0||1+1+1+0)
6((1+1+0|0+0+0)+1)=(1+1+0+0||1+1+0+0) + (1+1+1+0||0+0+0+0) + (1+1+2+2||0+0+0+0) + (1+1+0+0||0+0+0+0) + (1+1+2+2||1+1+0+0) + (1+1+1+0||1+1+0+0)
6((1+1+0|1+1+0)+1)=(1+1+0+0||1+1+1+0) + (1+1+0+0||1+1+0+0) + (1+1+1+0||1+1+0+0) + (1+1+2+2||1+1+0+0) + (1+1+2+2||1+1+2+2) + (1+1+0+0||1+1+2+2)
3((1+1+1|0+0+0)+1)=(1+1+1+0||1+1+0+0) + (1+1+1+0||0+0+0+0) + (1+1+1+1||0+0+0+0)
|---|---|--------------|
| 4 | | 0+0+0|0+0+0 |
| 6 | | 0+0+0|1+1+0 |
| 3 | | 0+0+0|1+1+1 |
| 6 | | 1+1+0|0+0+0 |
| 6 | | 1+1+0|1+1+0 |
| 3 | | 1+1+1|0+0+0 |
1个有4项,2个有3项,3个有6项
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 0 | 0 | 0 | | | 0 | 1 | 1 | 0 | 1 | | | 0 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | | 0 | | | 0 | 1 | 1 | | 1 | | | 0 | 0 | 1 | | 0 |
| 0 | 0 | | | | | | 0 | 0 | | | | | | 0 | 0 | | | |
| 0 | | | | | | | 0 | | | | | | | 0 | | | | |
| 0 | 0 | | | 0 | | | 0 | 0 | | | 0 | | | 0 | 0 | | | 0 |
| | | | | | | | | | | | | | | | | | | |
| | | | | | | | | | | | | | | | | | | |
| 0 | 0 | 0 | 0 | 0 | | | 0 | 0 | 0 | 0 | 0 | | | 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | | 0 | | | 0 | 1 | 1 | | 1 | | | 0 | 0 | 0 | | 0 |
| 1 | 1 | | | | | | 0 | 1 | | | | | | 1 | 1 | | | |
| 0 | | | | | | | 0 | | | | | | | 1 | | | | |
| 1 | 1 | | | 0 | | | 0 | 1 | | | 1 | | | 0 | 0 | | | 0 |
结果分布对称
求和
|---|---|---|---|---|
| 1 | 2 | 2 | 1 | 1 |
| 2 | 4 | 3 | | 2 |
| 2 | 3 | | | |
| 1 | | | | |
| 1 | 2 | | | 1 |
在极坐标平面上1+1不一定等于2,但仍然有秩序存在。