今天学习了数据链路层差错控制的三种方法,分别是:
奇偶校验法、循环冗余校验法和海明校验法。
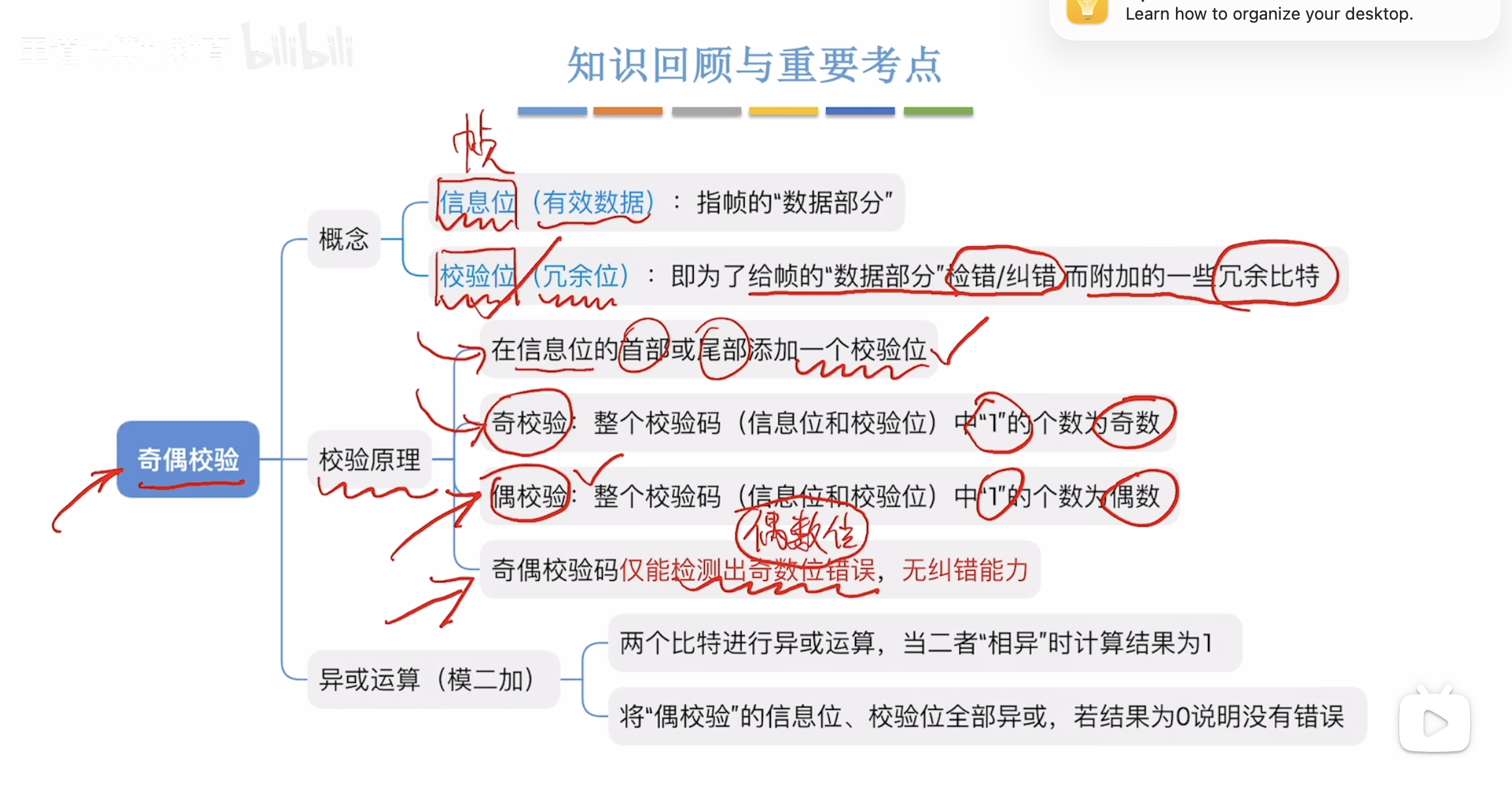
奇偶校验法是通过在信息位的首部添加校验位来实现,分为奇数校验法和偶数校验法。由于偶数校验法更适合通过异或(模2加)的方法实现,故现实中经常采用偶数校验法,即将信息位中的1和校验位的bit一起进行异或运算,如果异或结果为0,则说明总共有偶数个1,否则有奇数个1(错误)。但是如果同时存在两个位置的跳变,则偶数校验法无法检测出。
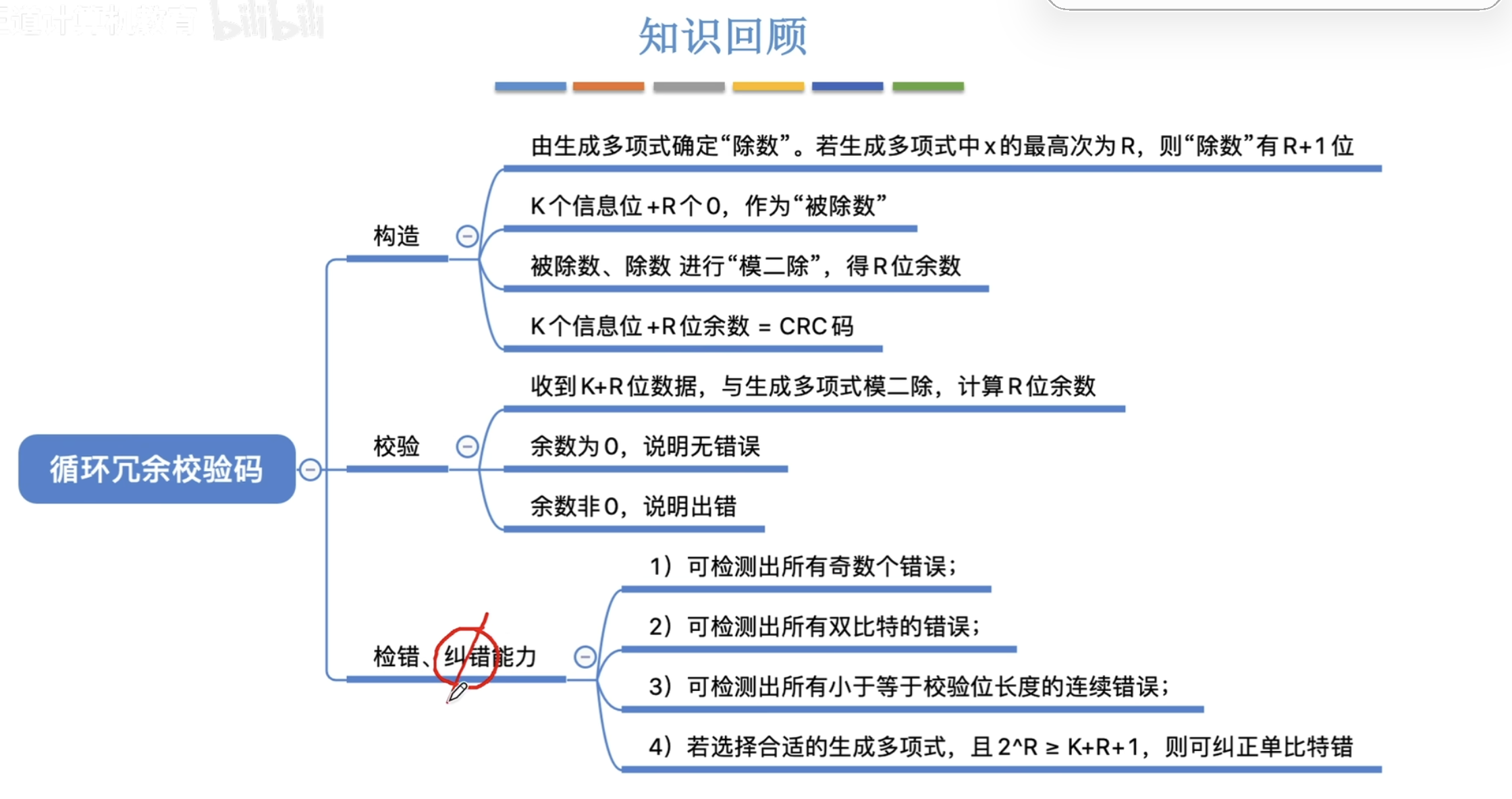
循环冗余校验法,就是设定一个生成多项式,例如 x 3 + x 2 + 1 x^3+x^2+1 x3+x2+1, 多项式的系数对应1101, 这个多项式为除数。然后在信息位的尾部添加多项式的次数(例子中为3)个bit位。如何确定这3个bit位呢?首先在信息位的末端填上3个0,然后开始进行模2除运算。最后的余数就是这3个校验位的bit. (不说多了,先记这么一点)
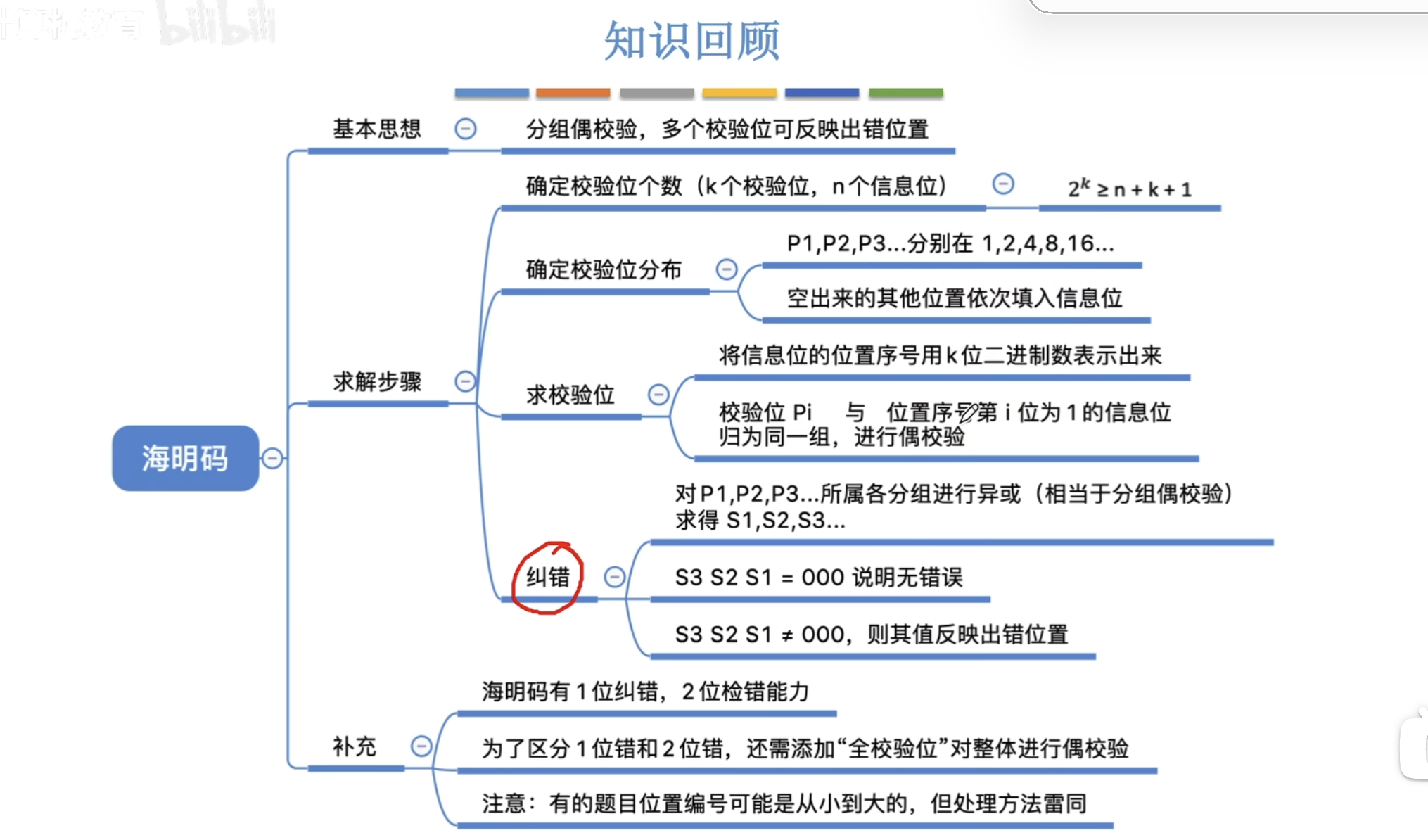
最后最厉害的是海明的海明校验法,海明因此发明创造获得了1986年的图灵奖。海明校验法是在奇偶校验发的基础上进一步改进,通过设置多个奇偶校验位,并且每一个校验位放的位置也不是规规矩矩地就放在信息位的首部,而是按照 2 i − 1 2^{i-1} 2i−1的方式来确定位置。例如设置3个校验位 P 1 P 2 P 3 P_1P_2P_3 P1P2P3, 这3个校验码在最终的信息码和校验码混合的整体bitc串中的位置分别是第1位,第2为,第4位。然后每一个校验码负责几个信息位的校验。假如原始信息码为 D 1 D 2 D 3 D 4 D_1D_2D_3D_4 D1D2D3D4, 如何对原始信息码进行分组呢?看下他们在最终bit串中的位置: P 1 P 2 D 1 P 3 D 2 D 3 D 4 P1P2D1P3D2D3D4 P1P2D1P3D2D3D4, D1 D2 D3 D4现在的位置分别是3、5、6、7, 转换成二进制分别是011,101,110,111。
则P1负责第1位为1的信息码:分别是D1,D2,D4;
P2负责第2位为1的信息码:D1,D3,D4,
P3 负责第3位为1的信息码 :D2,D3,D4.
这刚好对应:P3所在的位置刚好是4, 刚好对应最高位(第3位,2^2 = 4)
P2所在的位置刚好是2, 刚好对应第2位(第2位,2^1 = 2)
P1所在的位置刚好是1, 刚好对应第1位(第1位,2^0 = 1)
如果只出现了某一个位置的跳变,则可以定位出跳变的bit,并进行纠错。
但是如果两个位置同时跳变,会出现两个异或结果为1的情况,但是却不知道哪个位置出现了错误。所以海明校验法无法处理两个位置同时跳变的纠错。
学了这么多,只需要知道数据链路层进行差错控制有3种方法:分别是奇偶校验法、循环冗余校验法和海明校验法。海明校验法可以进行1位的纠错,无法进行2位的纠错,可以进行2位的检错。如果2个位置同时跳变了,是可以知道数据中存在错误的,但是不知道到底是哪两个位置出现了错误,这就叫做可以进行两个位置的检错,但是无法进行纠错。此时需要重传数据。