The 2025 China Collegiate Programming Contest (CCPC) Harbin Onsite Warmup
文章目录
- [A. 秘术「天文密葬法」](#A. 秘术「天文密葬法」)
- [B. 天才琪露诺与雾之湖宝藏](#B. 天才琪露诺与雾之湖宝藏)
- [C. 天才琪露诺与克劳恩皮丝](#C. 天才琪露诺与克劳恩皮丝)
- [D. 楼观楼观楼楼时间到了](#D. 楼观楼观楼楼时间到了)
A. 秘术「天文密葬法」
思路:考虑取模哈希,将阶乘值取模后存入map,然后遍历 i ∈ [ 1 , 10 6 ] i\in[1,10^6] i∈[1,106],查找map是否存在 i ⋅ n ! m i\cdot \frac{n!}{m} i⋅mn!取模后的值,若存在,则说明 i = m i=m i=m。
cpp
#include<bits/stdc++.h>
#define fi first
#define se second
#define lson (k<<1)
#define rson (k<<1)+1
#define mid ((l+r)/2)
#define pii pair<int,int>
#define bit bitset<100000>
using namespace std;
const int MAX=6e6+10;
const int MOD=998244353;
const long long INF=1e18;
const double PI=acos(-1.0);
typedef long long ll;
char s[MAX];
int solve()
{
const int m1=998244353;
const int m2=1000000007;
map<pii,int> ma;
ll a=1,b=1;
for(int i=1;i<=1000000;i++)
{
a=a*i%m1;
b=b*i%m2;
ma[{a,b}]=i;
}
scanf("%s",s);
int n=strlen(s);
a=b=0;
for(int i=0;i<n;i++)
{
a=(a*10+s[i]-'0')%m1;
b=(b*10+s[i]-'0')%m2;
}
for(int i=1;i<=1000000;i++)
{
auto it=ma.find({a*i%m1,b*i%m2});
if(it!=ma.end())return printf("%d %d\n", it->se,i);
}
return 0;
}
int main()
{
int T=1;
// cin>>T;
while(T--)solve();
return 0;
}B. 天才琪露诺与雾之湖宝藏
签到题。
cpp
#include<bits/stdc++.h>
#define fi first
#define se second
#define lson (k<<1)
#define rson (k<<1)+1
#define mid ((l+r)/2)
#define pii pair<int,int>
#define bit bitset<100000>
using namespace std;
const int MAX=6e6+10;
const int MOD=998244353;
const long long INF=1e18;
const double PI=acos(-1.0);
typedef long long ll;
int solve()
{
int n=1e9;
int x,y,a,b;
cin>>x>>y>>a>>b;
if(x==a)return printf("%d %d\n",x+(x==n?-1:1),y);
if(y==b)return printf("%d %d\n",x,y+(y==n?-1:1));
printf("%d %d\n",x,b);
return 0;
}
int main()
{
int T=1;
// cin>>T;
while(T--)solve();
return 0;
}C. 天才琪露诺与克劳恩皮丝
思路:仔细观察序列 g g g 的前几项,发现其是存在一定的循环规律的,如下:
1 2 1 4 1 2 1 8 1 2 1 4 1 2 1 \color{red}1\ 2\ 1\ 4\ 1\ 2\ 1\ 8\ 1\ 2\ 1\ 4\ 1\ 2\ 1 1 2 1 4 1 2 1 8 1 2 1 4 1 2 1 16
1 2 1 4 1 2 1 8 1 2 1 4 1 2 1 \color{red}1\ 2\ 1\ 4\ 1\ 2\ 1\ 8\ 1\ 2\ 1\ 4\ 1\ 2\ 1 1 2 1 4 1 2 1 8 1 2 1 4 1 2 1 32
1 2 1 4 1 2 1 8 1 2 1 4 1 2 1 \color{red}1\ 2\ 1\ 4\ 1\ 2\ 1\ 8\ 1\ 2\ 1\ 4\ 1\ 2\ 1 1 2 1 4 1 2 1 8 1 2 1 4 1 2 1 16
1 2 1 4 1 2 1 8 1 2 1 4 1 2 1 \color{red}1\ 2\ 1\ 4\ 1\ 2\ 1\ 8\ 1\ 2\ 1\ 4\ 1\ 2\ 1 1 2 1 4 1 2 1 8 1 2 1 4 1 2 1 64
1 2 1 4 1 2 1 8 1 2 1 4 1 2 1 \color{red}1\ 2\ 1\ 4\ 1\ 2\ 1\ 8\ 1\ 2\ 1\ 4\ 1\ 2\ 1 1 2 1 4 1 2 1 8 1 2 1 4 1 2 1 16
1 2 1 4 1 2 1 8 1 2 1 4 1 2 1 \color{red}1\ 2\ 1\ 4\ 1\ 2\ 1\ 8\ 1\ 2\ 1\ 4\ 1\ 2\ 1 1 2 1 4 1 2 1 8 1 2 1 4 1 2 1 32
1 2 1 4 1 2 1 8 1 2 1 4 1 2 1 \color{red}1\ 2\ 1\ 4\ 1\ 2\ 1\ 8\ 1\ 2\ 1\ 4\ 1\ 2\ 1 1 2 1 4 1 2 1 8 1 2 1 4 1 2 1 16
1 2 1 4 1 2 1 8 1 2 1 4 1 2 1 \color{red}1\ 2\ 1\ 4\ 1\ 2\ 1\ 8\ 1\ 2\ 1\ 4\ 1\ 2\ 1 1 2 1 4 1 2 1 8 1 2 1 4 1 2 1 128
即 g [ 1 , . . . , 15 ] = g [ 17 , . . . , 31 ] = . . . = g [ 16 ⋅ t + 1 , . . . , 16 ⋅ ( t + 1 ) − 1 ] g[1,...,15]=g[17,...,31]=...=g[16\cdot t+1,...,16\cdot(t+1)-1] g[1,...,15]=g[17,...,31]=...=g[16⋅t+1,...,16⋅(t+1)−1]
同理可以扩展到 g [ 1 , . . . , 511 ] = . . . = g [ 512 ⋅ t + 1 , . . . , 512 ⋅ ( t + 1 ) − 1 ] g[1,...,511]=...=g[512\cdot t+1,...,512\cdot(t+1)-1] g[1,...,511]=...=g[512⋅t+1,...,512⋅(t+1)−1]。
因为每511个数的间距是一样的,所以在做修改操作时,每隔511个数执行一下写操作即可;查询时只需统计 ∑ 0 ≤ i < 512 ( x − s i ) \sum_{0\leq i<512}(x-s_i) ∑0≤i<512(x−si)。
cpp
#include<bits/stdc++.h>
#define fi first
#define se second
#define lson (k<<1)
#define rson (k<<1)+1
#define mid ((l+r)/2)
#define sz(x) int(x.size())
#define pii pair<ll,ll>
#define bit bitset<100000>
using namespace std;
const int MAX=3e5+10;
const int MOD=998244353; //G=3
const int INF=INT_MAX/2;
const double PI=acos(-1.0);
typedef long long ll;
ll a[MAX],g[MAX],s[MAX];
int solve()
{
int n,m;
cin>>n>>m;
for(int i=1;i<=n;i++)
{
a[i]=0;
g[i]=(i%2?1:g[i/2]*2);
s[i]=s[i-1]+g[i];
}
ll ans=0;
while(m--)
{
ll op,x,w;
scanf("%lld%lld",&op,&x);
x^=ans;
if(op==1)
{
scanf("%lld",&w);
w=w^ans;
for(int i=0;i<=n&&x+s[i]<=n;i+=512)a[x+s[i]]+=w;
}
else
{
ans=0;
for(int i=0;i<512&&x-s[i]>=1;i++)ans+=a[x-s[i]];
printf("%lld\n",ans);
}
}
return 0;
}
int main()
{
int T=1;
// cin>>T;
while(T--)solve();
return 0;
}D. 楼观楼观楼楼时间到了
思路:考虑扫描线的思路,先将竹子和多边形一起绕圆点旋转,使竹子平行于 x x x 轴或 y y y 轴,利于计算,如下图黄色竹子平行于 y y y 轴。
对于一条穿过多边形的直线来说,其肯定会与多边形有偶数个交点(去除交于多边形顶点的情况),那么接下来就是统计这些交点坐标 y y y 值对答案的贡献。
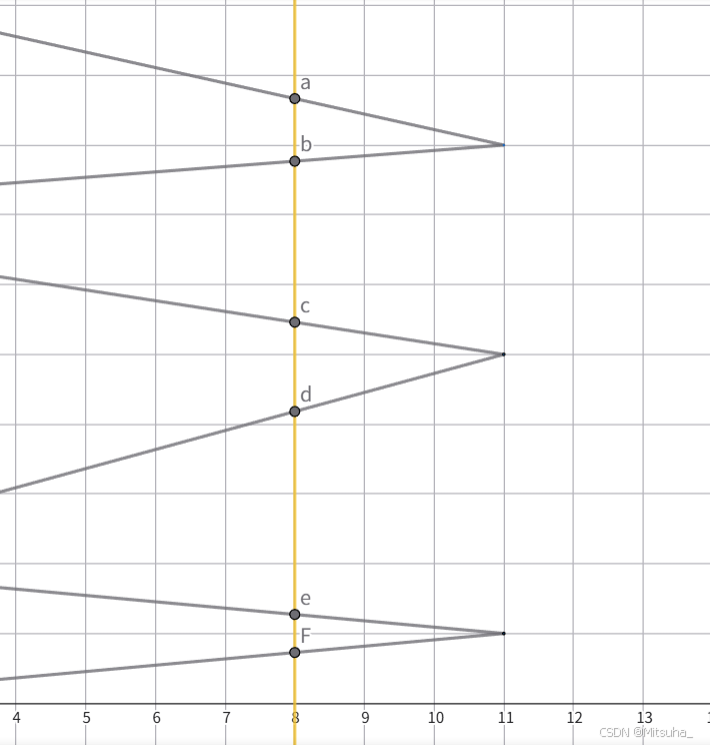
如上图,黄色竹子的贡献即为 y a − y b + y c − y d + y e − y f y_a-y_b+y_c-y_d+y_e-y_f ya−yb+yc−yd+ye−yf,所以我们可以遍历多边形的每条边,统计每条边与竹子相交顶点的 y y y 值对答案的贡献即可,同时每条边上贡献的 y y y 值构成等差数列,可以 O ( 1 ) O(1) O(1)求和。(需要注意处理顶点相交的情况)
如何知道这条边上的 y y y 值贡献是正是负呢,因为题目是按顺时针给出的多边形顶点,所以当遍历到边 A B AB AB 时,若 x A < x B x_A<x_B xA<xB则贡献是正的,否则是负的。
cpp
#include<bits/stdc++.h>
#define fi first
#define se second
#define lson (k<<1)
#define rson (k<<1)+1
#define mid ((l+r)/2)
#define sz(x) int(x.size())
#define pii pair<ll,ll>
#define bit bitset<100000>
using namespace std;
const int MAX=3e5+10;
const int MOD=998244353; //G=3
const int INF=INT_MAX/2;
const double PI=acos(-1.0);
typedef long long ll;
struct Point
{
double x,y;
Point(){}
Point(double x,double y):x(x),y(y){}
void show(){ printf("(%.10lf,%.10lf)\n",x,y);}
}p[MAX];
void clac(int n,double d)
{
double ans=0;
for(int i=0;i<n;i++)
{
Point A=p[i];
Point B=p[(i+1)%n];
Point C=p[(i+2)%n];
int tmp=(A.x<B.x?1:-1);
int a=A.x/d;
int b=B.x/d;
if(tmp<0&&a*d-A.x>1e-11)a+=tmp;
if(tmp>0&&A.x-a*d>1e-11)a+=tmp;
if(fabs(a*d-A.x)<1e-11)a+=tmp;
if(tmp<0&&B.x-b*d>1e-11)b-=tmp;
if(tmp>0&&b*d-B.x>1e-11)b-=tmp;
if(tmp*(b-a)+1<=0)continue;
double k=(A.y-B.y)/(A.x-B.x);
double a1=A.y+(a*d-A.x)*k;
double an=A.y+(b*d-A.x)*k;
ans+=tmp*(a1+an)*(tmp*(b-a)+1)/2;
}
printf("%.10lf\n",ans);
}
int solve()
{
int n;
cin>>n;
for(int i=0;i<n;i++)scanf("%lf%lf",&p[i].x,&p[i].y);
double a,d;
scanf("%lf%lf",&a,&d);
if(a!=90)
{
d=d*sin(a*PI/180);
double angle=(a-90)*PI/180;
for(int i=0;i<n;i++)
{
double x=p[i].x*cos(angle)+p[i].y*sin(angle);
double y=-p[i].x*sin(angle)+p[i].y*cos(angle);
p[i]={x,y};
}
}
clac(n,d);
return 0;
}
int main()
{
int T=1;
// cin>>T;
while(T--)solve();
return 0;
}