从自然常数 e 到复频域变换 | 欧拉恒等式与傅里叶 / 拉普拉斯变换的本质

斐夷所非2026-02-01 20:57

注：本文为 "从自然常数 e 到复频域变换的本质" 相关合辑。

图片清晰度受引文原图所限。

略作重排，如有内容异常，请看原文。

自然常数 e \boldsymbol {e} e：工程领域的自然基准量 1 \boldsymbol {1} 1

J Pan 编辑于 2020-06-18 20:36

客观世界中的所有研究对象，小至微观粒子，大至宏观宇宙，始终处于持续的运动与变化过程中。研究中通常采用函数描述自然现象的状态，采用变化率描述状态的变化特征。

1 基本概念定义

首先明确下述基本概念，为后续分析建立基础。

1.1 状态量与状态量的变化率

状态量是指描述事物当前状态的物理量，例如某根竹子的长度为 5 m，某个人的体重为 50 kg。状态量的变化率对应数学中导数的概念，定义为无穷小时间内状态增量与时间增量的比值，其数学表达式为：
f ′ ( t ) = lim ⁡ Δ t → 0 f ( t + Δ t ) − f ( t ) Δ t f'(t)=\lim_{\Delta t \rightarrow 0}{\frac {f (t+\Delta t)-f (t)}{\Delta t}} f′(t)=Δt→0limΔtf(t+Δt)−f(t)

1.2 单位状态量的变化率

单位状态量的变化率是指状态量的变化率与状态量的比值，其数学表达式为：
f ′ ( t ) ‾ = lim ⁡ Δ t → 0 f ( t + Δ t ) − f ( t ) Δ t ⋅ 1 f ( t ) = f ′ ( t ) f ( t ) \overline {f'(t)}=\lim_{\Delta t \rightarrow 0}{\frac {f (t+\Delta t)-f (t)}{\Delta t}\cdot\frac {1}{f (t)}}=\frac {f'(t)}{f (t)} f′(t)=Δt→0limΔtf(t+Δt)−f(t)⋅f(t)1=f(t)f′(t)

需明确上述两个定义的本质区别：状态量变化率属于宏观描述范畴，表征研究对象的整体变化特征；单位状态量变化率属于微观描述范畴，表征研究对象的局部变化特征。实际研究中，事物的局部变化规律通常由特定物理规律决定，与系统当前的整体状态无直接关联。例如竹子的生长规律，其各部位的生长特性保持一致，与竹子的当前总长度无关；细胞的分裂规律为固定形式，与系统当前的细胞总数无关。

2 连续变化问题的实例分析

考虑如下典型的连续变化物理问题：假设某竹苗的初始长度为 1 m，其生长过程为连续变化，单位增长率为 100%/ y e a r \mathrm {year} year/ m \mathrm {m} m（该参数为单位状态量的变化率），求解该竹苗在 1 年之后的长度。

2.1 初等静态分析的推导结果

( 1 + 100 % 1 ) 1 = 2 m \left (1+\frac {100\%}{1}\right)^1=2\ \mathrm {m} (1+1100%)1=2 m

该推导的局限性在于未遵循事物的连续变化特性，忽略了生长过程中新增量的持续生长效应，仅通过静态分析方法完成计算，无法反映动态的连续变化过程。

2.2 分步细化的推导结果

将单位增长率按时间尺度细化，取 100%/12/ m o n t h \mathrm {month} month/ m \mathrm {m} m，考虑每月新增量的生长效应，以月为单位累计 1 年的生长量，推导结果为：
( 1 + 100 % 12 ) 12 = 2.613 m \left (1+\frac {100\%}{12}\right)^{12}=2.613\ \mathrm {m} (1+12100%)12=2.613 m

若进一步按日细化，取 100%/365/ d a y \mathrm {day} day/ m \mathrm {m} m，以日为单位累计 1 年的生长量，推导结果为：
( 1 + 100 % 365 ) 365 = 2.714 m \left (1+\frac {100\%}{365}\right)^{365}=2.714\ \mathrm {m} (1+365100%)365=2.714 m

3 自然常数 e \boldsymbol{e} e的极限定义

上述推导仍未完全契合连续变化的本质，因为任意两个时间节点之间，竹子的生长过程仍在持续，前一时间段的新增量会在后续时间段中继续生长。欧拉针对该类连续变化问题给出了严格的极限求解方法，其数学表达式为：
lim ⁡ n → ∞ ( 1 + 100 % n ) n \lim_{n \rightarrow \infty}\left (1+\frac {100\%}{n}\right)^n n→∞lim(1+n100%)n

该式为高等数学中自然常数 e e e 的定义式，连续变化现象的数学本质均为极限问题，这是由连续的定义 ------ 自变量的增量趋于无穷小所决定。对于该极限式，需明确两个基本问题：极限是否收敛；若收敛，其数值为多少。欧拉证明了该极限存在且收敛，其数值约为 2.718，因此该常数也被称为欧拉常数 e e e，即：
lim ⁡ n → ∞ ( 1 + 100 % n ) n = e \lim_{n \rightarrow \infty}\left (1+\frac {100\%}{n}\right)^n=e n→∞lim(1+n100%)n=e

4 自然常数的指数函数形式

对自然常数 e e e的定义式进行简单变形，可得：
lim ⁡ n → ∞ [ ( 1 + 1 n / x ) n / x ] x = e x \lim_{n \rightarrow \infty}\left [\left (1+\frac {1}{n/x}\right)^{n/x}\right]^x=e^x n→∞lim[(1+n/x1)n/x]x=ex

由上述推导可得到结论：对于单位状态量的变化率为固定值的系统，其状态随时间的变化规律可由自然常数的指数函数描述。引入时间变量 t t t 后，该指数函数的一般形式为：
f ( t ) = e x t f (t)=e^{xt} f(t)=ext

当 x = 100 % x=100\% x=100% 时，函数形式简化为：
f ( t ) = e t f (t)=e^{t} f(t)=et

对该式求导并结合单位状态量变化率的定义，可得到结论：
100 % = f ′ ( t ) ‾ = f ′ ( t ) f ( t ) 100\%=\overline {f'(t)}=\frac {f'(t)}{f (t)} 100%=f′(t)=f(t)f′(t)

即指数函数 e t e^t et 的变化率与自身的状态值相等，这是指数函数的固有属性，该属性在自然常数 e e e 的定义中已隐含。

5 自然常数 e \boldsymbol{e} e的物理内涵

对自然常数 e e e 的物理内涵可作如下阐释：对于单位状态量的变化率为固定值（100%）的系统， e e e 代表该系统在 1 个单位时间内，由连续倍增增长所达到的极限值。典型实例为：存入 1 元本金至银行，若银行的年利率为 100%，按年计息的本利和为 2 元，按月计息的本利和为 2.613 元，若按无限小的时间尺度连续计息，本利和的极限值为 e e e 元。

从更本质的角度分析， e e e 描述了连续体变化或物体连续变化的特定状态 ------ 单位状态量的变化率为固定值，而自然界中多数事物的变化发展规律均接近该状态，这也是诸多物理量的变化曲线呈现指数形式的根本原因。简言之， e \boldsymbol {e} e 是对 "连续变化" 的数学表征。

欧拉恒等式的数学物理意义

J Pan 编辑于 2020-02-01 10:34

数系的扩展伴随人类对自然世界认知的深入而逐步推进，从自然数拓展至分数，进而拓展至无理数，最终拓展至复数。复数体系的抽象性使其成为数系学习中的难点，却为描述物理世界中的旋转、振动等现象提供了简洁的数学工具。本文将解析复数的本源意义，以及复数单位 i i i 与自然常数 e e e 结合后的数学特性与应用价值。

1 复数的发明与物理意义

在实数域内，加法与减法可表征为数轴上的左右平移，乘法与除法可表征为数轴上的拉伸与压缩，上述运算仅能描述一维的线性运动。而物理世界中广泛存在旋转运动，在复数发明之前，旋转问题的数学描述需通过复杂的坐标转换完成，缺乏简洁的表征方法。

复数的定义为虚数单位 i i i 的定义：

i = − 1 i=\sqrt {-1} i=−1

变形可得其运算性质：

i 2 = − 1 i^2=-1 i2=−1

从运算的物理意义解析，乘法可视为连续的变换操作，上式表明：实数 1 经过 2 次相同的变换操作后得到 -1，该变换操作的物理本质为绕坐标原点旋转 90 ∘ 90^\circ 90∘ 。由此可得复数的物理意义：虚数单位 i i i 是对平面旋转操作的数学表征。

2 e i x \boldsymbol {e}^{ix} eix 的数学特性与几何意义

自然常数 e e e 的指数函数定义为极限形式，表征事物的连续变化特性，其数学表达式为：
e x = lim ⁡ n → ∞ ( 1 + x n ) n e^x=\lim_{n \rightarrow \infty}\left (1+\frac {x}{n}\right)^n ex=n→∞lim(1+nx)n

将定义中的实数 x x x 替换为纯虚数 i x ix ix，可得复指数函数的定义式：
e i x = lim ⁡ n → ∞ ( 1 + i x n ) n e^{ix}=\lim_{n \rightarrow \infty}\left (1+\frac {ix}{n}\right)^n eix=n→∞lim(1+nix)n

通过 MATLAB 程序对该极限过程进行可视化分析，程序代码如下：

text 复制代码 
x=linspace (0,2*pi,50);%0 到 2pi 之间均匀布置 50 个点；
n=5000;% 此处可将 n 设成 20,50，500 或其他
e_ix=(1+x*1i./n).^n;
compass (e_ix);

程序的逻辑为：当 n → ∞ n \rightarrow \infty n→∞ 时， ( 1 + i x n ) n \left (1+\frac {ix}{n}\right)^n (1+nix)n 逐步收敛至 e i x e^{ix} eix。

当 n = 20 n=20 n=20 时：

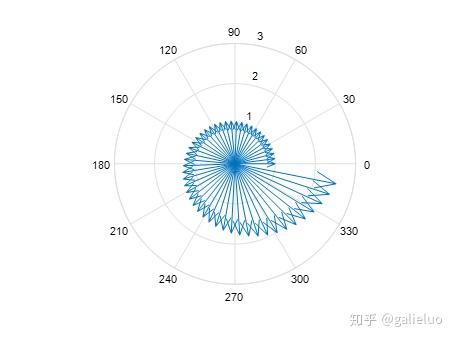
当 n = 50 n=50 n=50 时：

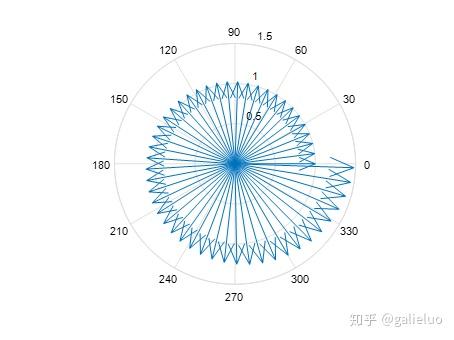
当 n = 500 n=500 n=500 时：

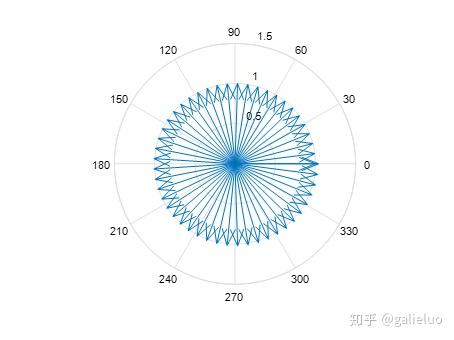
当 n = 5000 n=5000 n=5000 时：

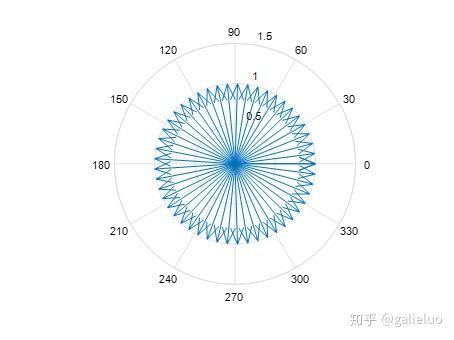
由可视化结果可得到结论：当 n n n 足够大时， e i x e^{ix} eix 的几何形态为复平面中的单位圆 。从矢量角度分析， e i x e^{ix} eix 表征复平面中的一族单位矢量，矢量的辐角为 x x x，矢量的幅值为 1。

3 欧拉恒等式的数学形式与物理意义

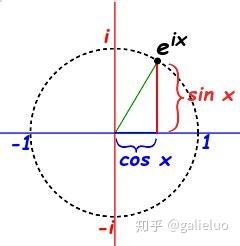
由 e i x e^{ix} eix 的几何意义可直接推导出欧拉公式的形式：
e i x = cos ⁡ x + i sin ⁡ x e^{ix}=\cos x + i\sin x eix=cosx+isinx

该公式将复指数函数与三角函数建立直接关联，实现了指数运算与三角运算的相互转换。令公式中的 x = π x=\pi x=π，可得欧拉恒等式：
e i π + 1 = 0 e^{i\pi}+1=0 eiπ+1=0

欧拉恒等式被认为是数学中形式最简洁、内涵最丰富的公式之一，该式将自然常数 e e e、圆周率 π \pi π、虚数单位 i i i、自然数 1、零元 0 这五个数学中最基本的常数，通过加法与等号两个基本运算符号连接，实现了数系与运算的高度统一。

从物理意义解析欧拉恒等式：自然数 1 对应的复平面矢量，经过 e i π e^{i\pi} eiπ 对应的变换操作后，再经过加法 1 的平移操作，最终回到坐标原点。其中 e i π e^{i\pi} eiπ 的物理意义为绕坐标原点旋转 180 ∘ 180^\circ 180∘ ，这也与 cos ⁡ π + i sin ⁡ π = − 1 \cos\pi + i\sin\pi = -1 cosπ+isinπ=−1 的运算结果一致。

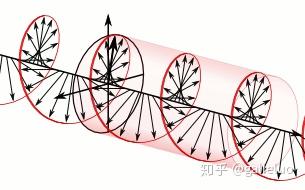
从本质上分析， e e e 表征连续变化， i i i 表征旋转操作，因此复指数函数 e i x e^{ix} eix 的物理意义为对平面内连续旋转运动的数学表征。该函数是描述振动、波动、旋转等周期性现象的基础数学工具，傅里叶变换与拉普拉斯变换均以复指数函数为基函数构建，成为工程领域分析线性系统的重要数学方法。

电磁波的传播规律与 e i x e^{ix} eix 的数学形式高度契合，光作为电磁波的一种，其传播过程也可通过复指数函数完成简洁表征。

傅里叶变换的数学本质：正交分解

J Pan，编辑于 2018-11-28 22:40

1 从数值组合到分解与正交的思想

人们常会提出这样的问题：为何世界各国的纸币面额多设定为 1、2、5 这三个数字？

该种面额设定是偶然选择还是必然结果？其背后的逻辑并无复杂的理论支撑，本质为追求计算与使用的简便性。人类在认知与实践的发展过程中，形成了将复杂问题拆解为简单问题的思维方式。例如，商品的价格具有多样性，但均可通过若干简单数字的线性叠加表示；1、2、5 这三个数字在 10 进制计数体系中，是实现该类叠加的最优组合形式。

为实现问题拆解的简洁性，人们提出了分解的思路；为提升分解的有效性，正交的概念被引入。正交的概念源于几何中的垂直，且其内涵较垂直更为丰富。在直角坐标系中，三个坐标轴两两相互垂直，该特性使各坐标轴对应的维度彼此独立、无相互耦合。上述描述仅为定性分析，无法满足数学与工程领域的严谨性要求。为此，内积的概念被提出，数学中规定：若两个量的内积为 0，则称这两个量正交。

梳理上述逻辑可得：为追求问题处理的简洁性，需对问题进行分解；为提升分解的有效性，需对分解方式进行正交化处理；为对正交化进行定量描述，需通过内积的定义实现，且内积为 0 是正交的定量判定条件。整体逻辑关系为：

简单→分解→正交→内积

上述内容与傅里叶分析的关联在于：傅里叶分析的本质是对函数进行正交分解。即便暂未理解正交分解的细节，只要建立该概念认知，便可把握傅里叶分析的基本内涵。下文将逆序梳理上述逻辑，从内积的概念出发展开分析，以保证推导的严谨性。

2 三维向量空间的正交分解与内积运算

在三维直角坐标系中，沿各坐标轴方向、模长为 1 的向量被称为基向量，两两相互垂直的基向量被称为正交基。如： ( 1 , 0 , 0 ) (1,0,0) (1,0,0) 为 x x x 轴对应的正交基， ( 0 , 1 , 0 ) (0,1,0) (0,1,0) 为 y y y 轴对应的正交基， ( 0 , 0 , 1 ) (0,0,1) (0,0,1) 为 z z z 轴对应的正交基。设向量 x ⃗ = ( a 1 , b 1 , c 1 ) \vec{x}=(a_1,b_1,c_1) x =(a1,b1,c1)， y ⃗ = ( a 2 , b 2 , c 2 ) \vec{y}=(a_2,b_2,c_2) y =(a2,b2,c2)，定义二者的内积为：
⟨ x ⃗ , y ⃗ ⟩ = ⟨ ( a 1 , b 1 , c 1 ) , ( a 2 , b 2 , c 2 ) ⟩ = a 1 a 2 + b 1 b 2 + c 1 c 2 \langle \vec{x},\vec{y} \rangle = \langle (a_1,b_1,c_1),(a_2,b_2,c_2) \rangle = a_1a_2 + b_1b_2 + c_1c_2 ⟨x ,y ⟩=⟨(a1,b1,c1),(a2,b2,c2)⟩=a1a2+b1b2+c1c2

由内积定义可推导得如下结论：
⟨ ( 1 , 0 , 0 ) , ( 0 , 1 , 0 ) ⟩ = 1 × 0 + 0 × 1 + 0 × 0 = 0 \langle (1,0,0),(0,1,0) \rangle = 1\times0 + 0\times1 + 0\times0 = 0 ⟨(1,0,0),(0,1,0)⟩=1×0+0×1+0×0=0

该结果表明三维直角坐标系中的任意两个正交基满足正交的定量判定条件。
⟨ ( 1 , 0 , 0 ) , ( 1 , 0 , 0 ) ⟩ = 1 × 1 + 0 × 0 + 0 × 0 = 1 \langle (1,0,0),(1,0,0) \rangle = 1\times1 + 0\times0 + 0\times0 = 1 ⟨(1,0,0),(1,0,0)⟩=1×1+0×0+0×0=1

该结果表明一个向量与其自身的内积为非零常数。

线性代数中，任意一个三维向量均可由正交基的线性组合表示。以向量 v ⃗ = ( 5 , 2 , 7 ) \vec{v}=(5,2,7) v =(5,2,7) 为例，其分解过程如下：

A = ⟨ v ⃗ , x ⃗ ⟩ = ⟨ ( 5 , 2 , 7 ) , ( 1 , 0 , 0 ) ⟩ = 5 B = ⟨ v ⃗ , y ⃗ ⟩ = ⟨ ( 5 , 2 , 7 ) , ( 0 , 1 , 0 ) ⟩ = 2 C = ⟨ v ⃗ , z ⃗ ⟩ = ⟨ ( 5 , 2 , 7 ) , ( 0 , 0 , 1 ) ⟩ = 7 \begin{align} A &= \langle \vec{v},\vec{x} \rangle = \langle (5,2,7),(1,0,0) \rangle = 5 \tag{1} \\ B &= \langle \vec{v},\vec{y} \rangle = \langle (5,2,7),(0,1,0) \rangle = 2 \tag{2} \\ C &= \langle \vec{v},\vec{z} \rangle = \langle (5,2,7),(0,0,1) \rangle = 7 \tag{3} \end{align} ABC=⟨v ,x ⟩=⟨(5,2,7),(1,0,0)⟩=5=⟨v ,y ⟩=⟨(5,2,7),(0,1,0)⟩=2=⟨v ,z ⟩=⟨(5,2,7),(0,0,1)⟩=7(1)(2)(3)

由此可得 v ⃗ = A x ⃗ + B y ⃗ + C z ⃗ \vec{v}=A\vec{x}+B\vec{y}+C\vec{z} v =Ax +By +Cz 。由该分解过程可归纳出内积的几何意义：内积对应投影运算，任意向量与某一正交基的内积，即为该向量在该正交基所在方向上的投影值，且该投影值为向量分解中对应正交基的系数。

上述分析中的基为常数形式的基向量，该类基的相关知识因与三维物理空间对应，且从初中阶段便被逐步引入，因此易于理解。下文将对上述正交分解的思路进行推广，推导过程中将呈现出更具一般性的结论。

3 函数空间的内积定义与正交基推广

若将正交分解的基由向量推广为函数，可得到函数空间中的正交分解理论。设 f ( t ) f(t) f(t)、 g ( t ) g(t) g(t) 为函数空间中的两个函数，定义二者的内积为：
⟨ f , g ⟩ = ∫ − ∞ + ∞ f ( t ) ⋅ g ( t ) ‾ d t \langle f,g \rangle = \int_{-\infty}^{+\infty}f(t) \cdot \overline{g(t)} dt ⟨f,g⟩=∫−∞+∞f(t)⋅g(t)dt

其中 g ( t ) ‾ \overline{g(t)} g(t) 为 g ( t ) g(t) g(t) 的共轭函数，该定义的引入是为了方便复数域内的内积计算。

自然常数 e e e 与复指数函数 e i x e^{ix} eix 具有特殊的数学性质，将复指数函数代入函数空间的内积定义中，可推导其正交性。设 f ( t ) = e i ω 1 t f(t)=e^{i\omega_1 t} f(t)=eiω1t， g ( t ) = e i ω 2 t g(t)=e^{i\omega_2 t} g(t)=eiω2t，根据函数空间的内积定义，二者的内积为：
⟨ f , g ⟩ = ∫ − ∞ + ∞ e i ω 1 t ⋅ e − i ω 2 t d t = ∫ − ∞ + ∞ e i ( ω 1 − ω 2 ) t d t \langle f,g \rangle = \int_{-\infty}^{+\infty}e^{i\omega_1 t} \cdot e^{-i\omega_2 t} dt = \int_{-\infty}^{+\infty}e^{i(\omega_1-\omega_2)t} dt ⟨f,g⟩=∫−∞+∞eiω1t⋅e−iω2tdt=∫−∞+∞ei(ω1−ω2)tdt

4 复指数函数族的正交性验证与完备性

复指数函数族 { e i ω t } \{e^{i\omega t}\} {eiωt} 的正交性可通过内积运算分两种情况验证，其结果是后续傅里叶变换推导的重要基础。

4.1 正交性验证

1. 当 ω 1 ≠ ω 2 \omega_1 \neq \omega_2 ω1=ω2 时

复指数函数 e i x e^{ix} eix 的几何意义为复平面内绕原点旋转的单位向量，这一特性可通过以下Matlab代码直观验证：

matlab 复制代码 
x=linspace(0,2*pi,50);% 0 到 2π 之间均匀布置 50 个点
n=5000;% 可修改为 20、50、500 等数值观察变化
e_ix=(1+x*1i./n).^n;
compass(e_ix);% 绘制复向量罗盘图
figure;
polarplot(e_ix);% 绘制极坐标图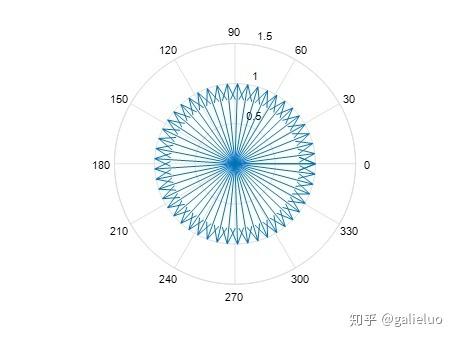

基于 e i ( ω 1 − ω 2 ) t e^{i(\omega_1-\omega_2)t} ei(ω1−ω2)t 的旋转对称性可推得，此时两个复指数函数的内积结果为 0，即：

⟨ f , g ⟩ = ⟨ e i ω 1 t , e i ω 2 t ⟩ = ∫ − ∞ + ∞ e i ( ω 1 − ω 2 ) t d t = 0 \langle f,g \rangle = \langle e^{i\omega_1 t},e^{i\omega_2 t} \rangle = \int_{-\infty}^{+\infty}e^{i(\omega_1-\omega_2)t} dt = 0 ⟨f,g⟩=⟨eiω1t,eiω2t⟩=∫−∞+∞ei(ω1−ω2)tdt=0

该结果满足正交性的定量判定条件，说明复指数函数族 { e i ω t } \{e^{i\omega t}\} {eiωt} 在该内积定义下构成函数空间中的一族正交基。

2. 当 ω 1 = ω 2 \omega_1 = \omega_2 ω1=ω2 时

上述积分的结果为无穷大，该结果在广义函数理论中具有合理性，直接给出其积分表达式：

⟨ f , g ⟩ = 2 π ⋅ δ ( ω 1 − ω 2 ) \langle f,g \rangle = 2\pi \cdot \delta(\omega_1-\omega_2) ⟨f,g⟩=2π⋅δ(ω1−ω2)

其中 δ ( ⋅ ) \delta(\cdot) δ(⋅) 为狄拉克δ函数，相关理论下文暂不展开。

4.2 完备性与傅里叶逆变换雏形

借助深入的数学理论可证明：在特定条件下，复指数函数族 { e i ω t } \{e^{i\omega t}\} {eiωt} 不仅具有正交性，还具备完备性。

完备性的含义为：满足该条件的任意函数 f ( t ) f(t) f(t)，均可由复指数函数族 { e i ω t } \{e^{i\omega t}\} {eiωt} 线性叠加表示，具体分两种形式：

1. 离散型（傅里叶级数）

适用于周期函数，其角频率取离散值，叠加形式为求和运算：

f ( t ) = ∑ ω = − ∞ + ∞ A ω e i ω t f(t)=\sum_{\omega=-\infty}^{+\infty}A_\omega e^{i\omega t} f(t)=ω=−∞∑+∞Aωeiωt

其中 A ω A_\omega Aω 为离散角频率对应的叠加系数，仅需可数无限项求和即可完成函数分解。

2. 连续型（傅里叶逆变换）

适用于非周期函数，其角频率取全体实数（连续区间），离散求和无法表示连续频率的叠加，需通过积分运算实现，表达式（即傅里叶逆变换的雏形）为：

f ( t ) = 1 2 π ∫ − ∞ + ∞ F ( ω ) e i ω t d ω (4) f(t) = \frac{1}{2\pi}\int_{-\infty}^{+\infty}F(\omega)e^{i\omega t} d\omega \tag{4} f(t)=2π1∫−∞+∞F(ω)eiωtdω(4)

式 (4) 的数学内涵为：任意非周期函数 f ( t ) f(t) f(t) 可由完备正交基 { e i ω t } \{e^{i\omega t}\} {eiωt} 线性叠加重构，其中 F ( ω ) F(\omega) F(ω) 为正交基 e i ω t e^{i\omega t} eiωt 对应的连续型叠加系数。式中系数 1 / 2 π 1/2\pi 1/2π 的引入是为了简化傅里叶变换与逆变换的配套计算，傅里叶变换存在多种表达形式，本文采用工程与数学领域最通用的该形式，部分表达形式中未引入该系数。

5 傅里叶变换与逆变换的推导

5.1 傅里叶变换的定义（叠加系数求解）

类比三维向量正交分解的系数求解方法（式 (1)、式 (2)、式 (3)），函数空间中正交基的叠加系数 F ( ω ) F(\omega) F(ω) 可通过内积运算求解，其表达式为：

F ( ω ) = ⟨ f ( t ) , e i ω t ⟩ = ∫ − ∞ + ∞ f ( t ) e − i ω t d t (5) F(\omega) = \langle f(t),e^{i\omega t} \rangle = \int_{-\infty}^{+\infty}f(t)e^{-i\omega t} dt \tag{5} F(ω)=⟨f(t),eiωt⟩=∫−∞+∞f(t)e−iωtdt(5)

明确定义：

  • 式 (5) 被定义为傅里叶变换
  • 式 (4) 被定义为傅里叶逆变换

5.2 变换与逆变换的本质

1. 傅里叶变换的本质

是函数空间中的正交分解：对 f ( t ) f(t) f(t) 与复指数正交基 e i ω t e^{i\omega t} eiωt 进行内积运算时，仅 f ( t ) f(t) f(t) 中角频率为 ω \omega ω 的分量会产生非零内积结果，其余角频率分量与 e i ω t e^{i\omega t} eiωt 的内积均为 0；该内积的积分区间为 t ∈ ( − ∞ , + ∞ ) t \in(-\infty,+\infty) t∈(−∞,+∞)，运算结果为 f ( t ) f(t) f(t) 对应信号在正交基 e i ω t e^{i\omega t} eiωt 上的整体投影，任意给定角频率 ω \omega ω 均存在唯一对应的叠加系数 F ( ω ) F(\omega) F(ω)，该系数表征 f ( t ) f(t) f(t) 中角频率为 ω \omega ω 分量的大小。

2. 傅里叶逆变换的本质

是基于投影系数的函数重构：通过各正交基 e i ω t e^{i\omega t} eiωt 的线性组合，可由傅里叶变换结果 F ( ω ) F(\omega) F(ω) 还原原函数 f ( t ) f(t) f(t)。

5.3 工程价值总结

傅里叶变换实现了函数从时间域到频率域的转换，为分析信号频率特性、求解线性系统响应等工程问题，提供了简洁高效的数学方法。

总结

  • 逻辑：正交性验证（分两种 ω \omega ω 情况）→ 完备性（离散求和/连续积分）→ 傅里叶变换（求系数）与逆变换（重构函数）→ 工程应用。
  • 区分：求和形式（周期函数、离散频率）是傅里叶级数，积分形式（式4，非周期函数、连续频率）是傅里叶逆变换，后者是本文规范形式。
  • 本质：傅里叶变换是正交分解（时间域→频率域），逆变换是线性叠加重构（频率域→时间域）， 1 / 2 π 1/2\pi 1/2π 是通用形式的简化配套系数。

从另一视角解析拉普拉斯变换

J Pan，编辑于 2021-06-12 23:10

拉普拉斯变换是现代工程领域应用最为广泛的数学工具之一，该变换借助数学映射，将微积分方程转化为代数方程，为连续空间与连续时间域内方程的求解提供了可行路径。

现有教材通常直接给出拉普拉斯变换的数学定义，未对其发展历史与内在数学内涵展开阐释，这使得诸多学习者对该变换的理解存在障碍。

本文将从不同视角解析拉普拉斯变换的本质，相关研究将从一位在科学史上被严重低估的学者展开------奥列弗·赫维赛德（Oliver Heaviside）。

一、 奥列弗·赫维赛德的学术背景与贡献

奥列弗·赫维赛德（Oliver Heaviside）是维多利亚时期的英国学者，他出身于贫困家庭，患有听力障碍，且曾罹患猩红热，未接受过正规大学教育，依靠自学与研究兴趣掌握了高等科学与数学知识。

多数学习者对赫维赛德的认知源于 MATLAB 中的赫维赛德（Heaviside）函数，该函数为阶跃函数，与狄拉克（Dirac）函数存在密切的数学关联。

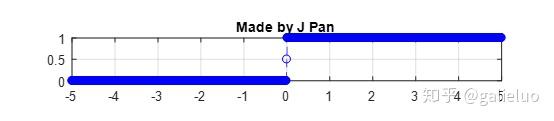
本文对赫维赛德的探讨并非围绕该函数展开，而是聚焦其对麦克斯韦方程组的重构工作------麦克斯韦本人并未见到现今形式的方程组，该方程组在一定意义上亦可被称作"赫维赛德方程组"。

使用 LaTeX 的 align* 环境可实现等号列对齐，校对后格式如下：
∇ ⋅ D = ρ v ∇ ⋅ B = 0 ∇ × E = − ∂ B ∂ t ∇ × H = ∂ D ∂ t + J \begin{align*} \nabla \cdot \mathbf{D} &= \rho_v \\ \nabla \cdot \mathbf{B} &= 0 \\ \nabla \times \mathbf{E} &= -\frac{\partial \mathbf{B}}{\partial t} \\ \nabla \times \mathbf{H} &= \frac{\partial \mathbf{D}}{\partial t} + \mathbf{J} \end{align*} ∇⋅D∇⋅B∇×E∇×H=ρv=0=−∂t∂B=∂t∂D+J

该方程组的四个表达式具有高度的对称性，其物理内涵明确：变化的电场激发磁场，变化的磁场激发电场。电磁波的传播过程即为电场与磁场相互转化、交替激发并向空间传播的过程。正是得益于赫维赛德的重构工作，麦克斯韦电磁理论在 19 世纪末得以确立并得到广泛传播。宇宙中所有电磁现象（包含光现象）均可由麦克斯韦方程组进行阐释，该方程组实现了电磁场的统一描述，这也促使爱因斯坦试图以相同的数学方式完成引力场的统一，并将宏观与微观的相互作用纳入同一套数学体系，即著名的"大一统理论"，爱因斯坦并未完成这一研究目标。

麦克斯韦于 1873 年出版了具有划时代意义的著作《电磁通论》，但其英年早逝，所提出的电磁理论方程组在其生前未得到科学界的关注。其中一项重要原因是其理论的数学表述极为复杂，最初提出的电磁理论包含 20 个方程，这使得该理论在首次发表后的 10 余年里，几乎未被学界研究。

赫维赛德对麦克斯韦原始方程组进行了系统化简化，他凭借敏锐的学术洞察力，挖掘出麦克斯韦方程所蕴含的深层物理内涵，简化后的麦克斯韦方程组展现出极致的对称性，成为数学物理领域极具美学特征的方程组。

赫维赛德的另一项重要学术贡献为运算微积分的创立。电磁学领域的诸多定理与公式，在历史发展过程中均以微积分形式进行表述。1880 年至 1887 年，赫维赛德在开展电磁场研究的同时，为实现微积分方程的求解，在数值分析与计算中引入了微分算子的概念，该方法的数学特征为：将常微分方程转化为普通代数方程。赫维赛德通过直观的数学直觉构建了微分方程的求解方法，他将微分与积分运算通过统一的算子进行表示。

  • 微分算子用 p p p 表示：
    p ↔ d ( ) d x p\leftrightarrow\frac{\mathrm{d}()}{\mathrm{d}x} p↔dxd()
  • 高阶微分算子为：
    p n ↔ d n ( ) d t n p^n\leftrightarrow\frac{\mathrm{d}^n()}{\mathrm{d}t^n} pn↔dtndn()
  • 积分算子符号用 1 p \frac{1}{p} p1 表示：
    1 p ( ) ↔ ∫ − ∞ t ( ) d τ \frac{1}{p}()\leftrightarrow\int_{-\infty}^{t}()\mathrm{d}\tau p1()↔∫−∞t()dτ

即在该算子体系下，积分运算与微分运算呈现倒数关系。赫维赛德未对算子 p p p 的数学本质进行详细阐释，在缺乏严格数学证明的前提下，将该方法应用于学术研究并发表相关成果。例如常见的二阶常微分方程：
m d 2 x d t 2 + c d x d t + k x = 0 m\frac{\mathrm{d}^2x}{\mathrm{d}t^2}+c\frac{\mathrm{d}x}{\mathrm{d}t}+kx=0 mdt2d2x+cdtdx+kx=0

采用赫维赛德的微分算子变换后，可转化为如下代数表达式：
m p 2 + c p + k = 0 mp^2+cp+k=0 mp2+cp+k=0

赫维赛德基于物理直觉构建了该算子方法，该方法因缺乏严格的数学基础，受到当时主流数学家的质疑，学界认为其研究缺乏理论依据，属于非规范的数学推导。赫维赛德对该质疑作出了回应，其观点为：因为我不能理解消化过程就拒绝晚餐吗？不，只要我满意这个结果。

赫维赛德所创立的微积分算子体系，为拉普拉斯变换的提出奠定了理论基础，是拉普拉斯变换的前身。赫维赛德的算子方法虽缺乏严格的数学证明，但其在实际应用中能够得到正确的求解结果，该方法的有效性得到了实践验证。19 世纪与 20 世纪之交，数学家开始对该算子理论进行严格的数学证明。研究者在法国数学家拉普拉斯于 70 年前发表的概率论著作中，找到了该算子方法的数学依据，该著作中提出的数学变换并非现今的拉普拉斯变换，而是 Z 变换。

拉普拉斯变换并非由拉普拉斯直接提出，第二次世界大战后，拉普拉斯变换得到广泛应用，赫维赛德算子的实际应用场景逐渐减少，但该非规范的、基于数学直觉创立的方法，推动了拉普拉斯分析方法的形成与发展。

二、 傅里叶变换（拉普拉斯变换的轻量形式）

在解析拉普拉斯变换之前，首先对傅里叶变换予以阐释，傅里叶变换可视为拉普拉斯变换的轻量形式。傅里叶变换的数学思想为：自然界中诸多物理现象的数学表达，均可分解为三角函数的线性组合。

图片来源：www.bolvan.ph.utexas.edu

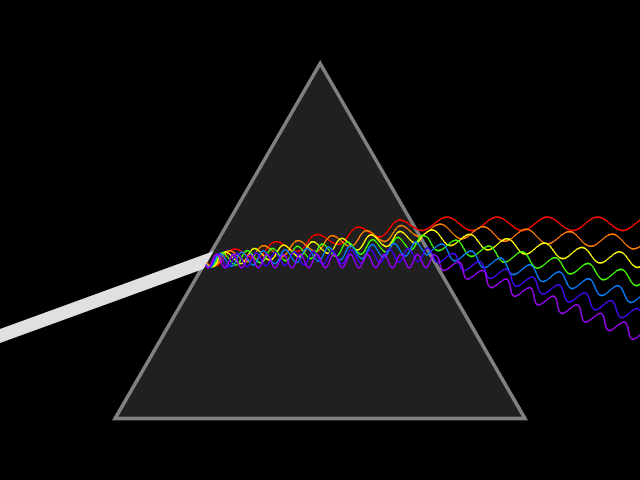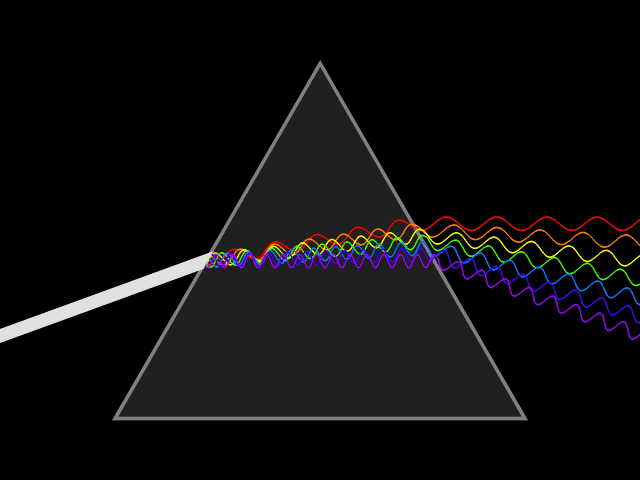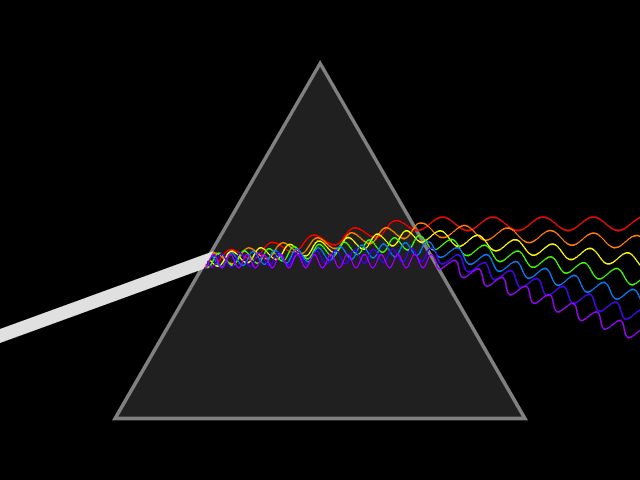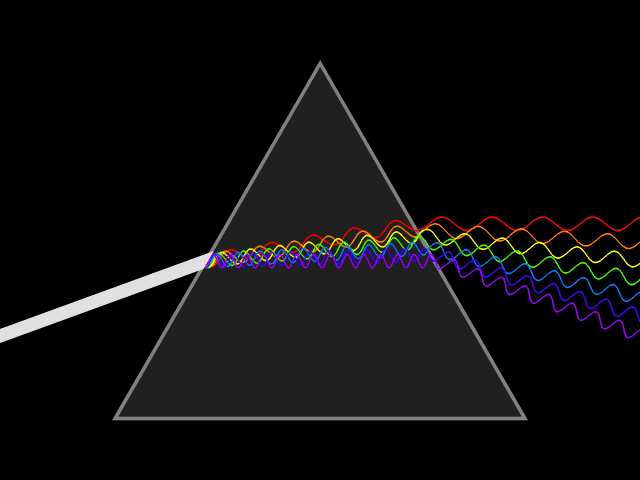
古巴比伦研究者较早将三角函数与数值逼近方法应用于天体运动的观测与预报；1748 年，欧拉采用类似方法对弦的振动问题进行分析；1753 年，伯努利提出任意物理弦的振动均可表示为三角函数的和，但其未给出严格的数学证明。注：伯努利为科学世家，该家族 3 代中共诞生 8 位科学家，有不少于 120 位后裔被系统记载于科学史中。

1807 年，傅里叶向法国科学学会提交论文，将正弦曲线应用于温度分布的数学描述，该论文中提出了一项具有争议的观点：任意连续周期信号均可由一组适当的正弦曲线线性组合表示。傅里叶未对该观点进行严格的数学论证。该论文的审稿人包含拉格朗日与拉普拉斯等著名数学家，拉普拉斯与其他审稿人投票同意发表该论文，而拉格朗日坚决反对，其认为傅里叶的方法无法对带有棱角的信号进行准确表示。法国科学学会受拉格朗日学术影响力的影响，拒绝发表该论文。1822 年，傅里叶变换随其著作《热的解析理论》正式发表，距其首次提交论文已时隔 15 年。1829 年，狄利克雷通过推导傅里叶变换的适用条件，完成了对傅里叶变换的系统化完善。

三角函数与复指数函数可通过欧拉公式建立数学关联，其表达式为：
e i ω t = cos ⁡ ( ω t ) + i sin ⁡ ( ω t ) e^{i\omega t}=\cos(\omega t)+i\sin(\omega t) eiωt=cos(ωt)+isin(ωt)

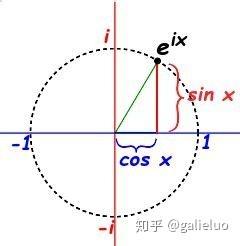
复指数函数与正弦函数、余弦函数存在紧密的数学关联，基于此可进一步探讨：部分信号是否亦可分解为复指数函数的线性组合？首先对复指数函数 e i ω t e^{i\omega t} eiωt 的数学性质进行分析。

相关研究中已得到如下结论：自然常数 e e e 可对事物的连续变化过程进行数学描述；虚数单位 i = − 1 = e i π 2 i=\sqrt{-1}=e^{i\frac{\pi}{2}} i=−1 =ei2π 可对旋转过程进行数学表征；复指数函数 e i ω t e^{i\omega t} eiωt 对应复平面中连续旋转的单位圆。（对该结论存在疑惑者，可参考相关研究文献，其中包含详细推导过程）。

当角频率 ω = 1 r a d / s \omega=1\ \mathrm{rad/s} ω=1 rad/s 时：

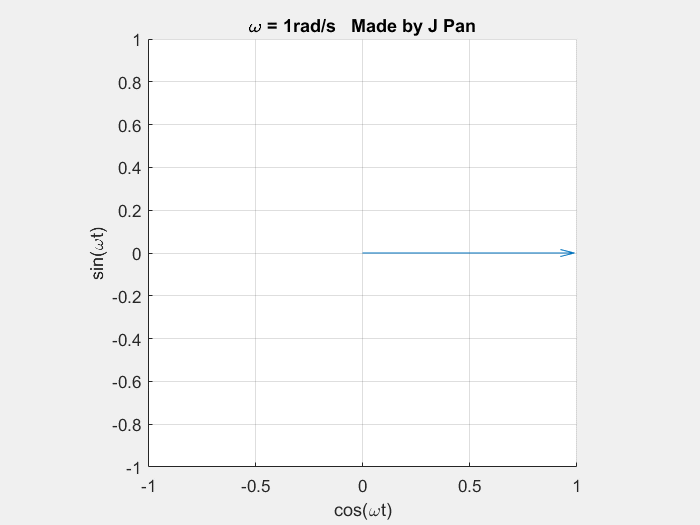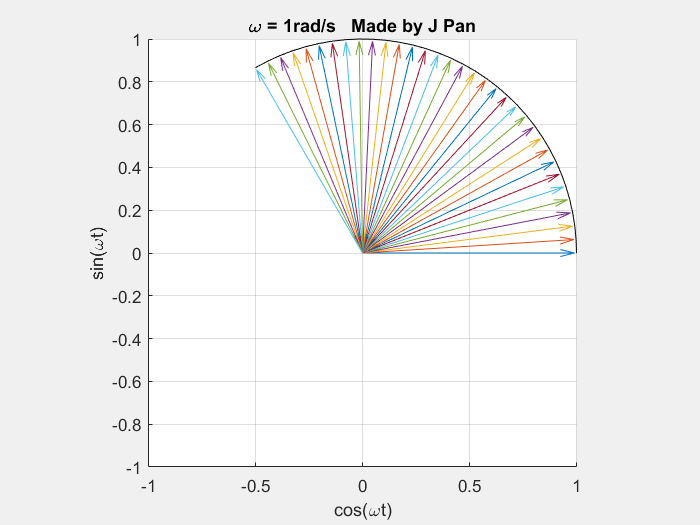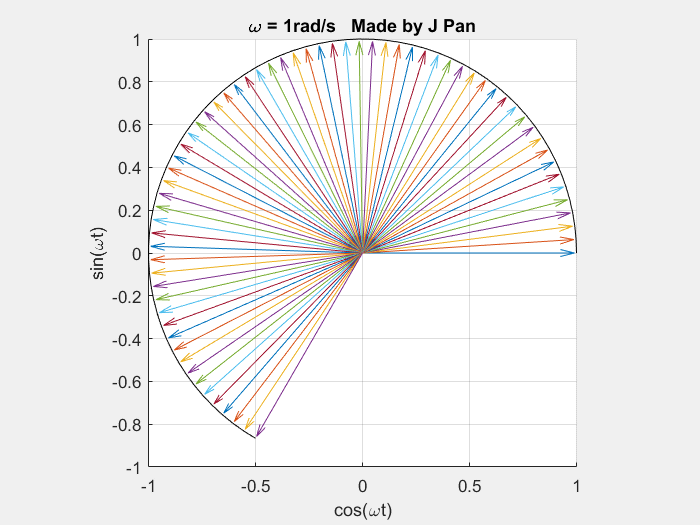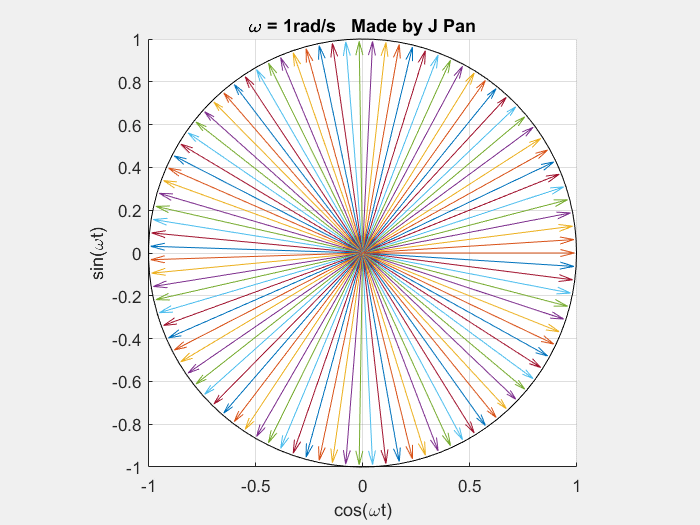
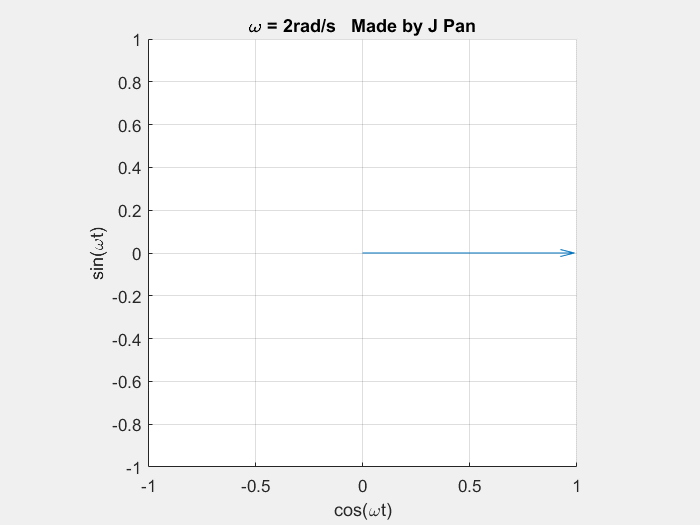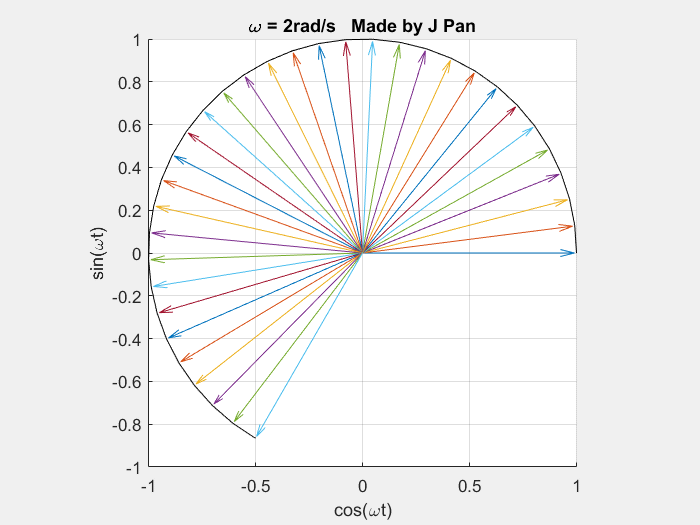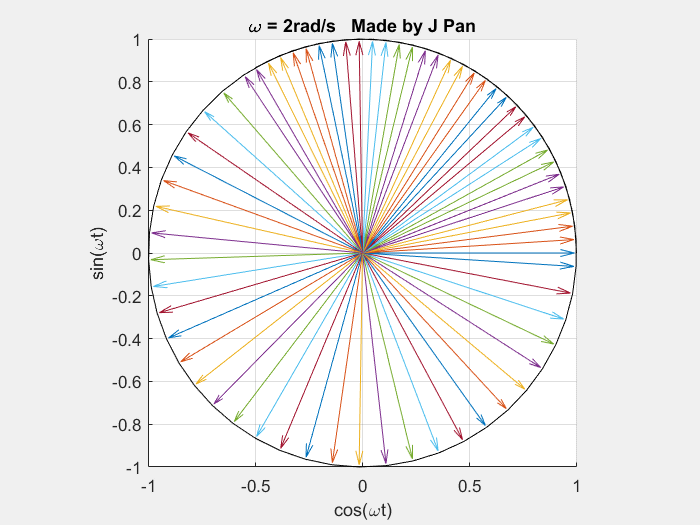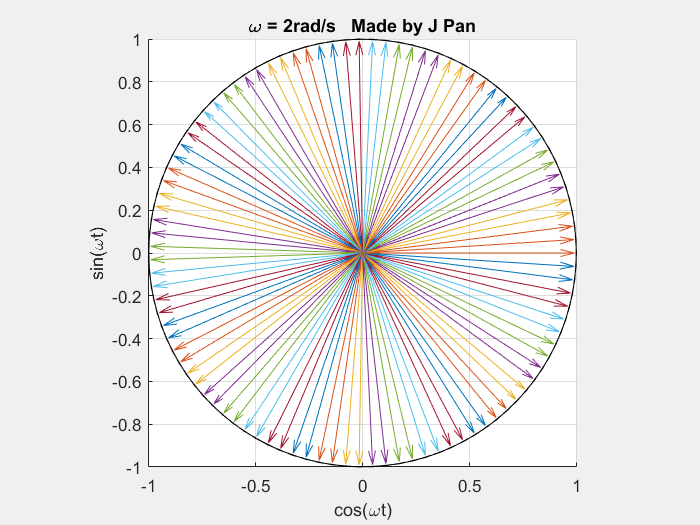
当角频率 ω = 2 r a d / s \omega=2\ \mathrm{rad/s} ω=2 rad/s 时：

matlab 复制代码 
clc;clear;
h = animatedline;
xl=xlabel('cos(\omega t)');%
yl=ylabel('sin(\omega t)');%
grid on;
title('\omega = 1\mathrm{rad/s}   Made by J Pan')
axis([-1,1,-1,1]);
axis square;
N = 100;
t=linspace(0,2*pi,N);
w=1;
x=cos(w*t);
y=sin(w*t);
a = tic; % start timer
for k = 1:N
    addpoints(h,x(k),y(k));
    hold on
    quiver(0,0,x(k)*1.1,y(k)*1.1)
    b = toc(a); % check timer
    if b > (1/90)
        drawnow % update screen every 1/30 seconds
        a = tic; % reset timer after updating
    end
end

因此，复指数函数族 { e i ω t } \{e^{i\omega t}\} {eiωt} 为复平面中幅值恒为 1、角频率可变的连续旋转曲线族。诸多信号的数学曲线，均可由不同角频率的连续旋转单位圆通过线性叠加得到，傅里叶变换即为该结论的数学表述。傅里叶变换的基本表述为：任意满足狄利克雷条件的函数，均可分解为复指数函数的线性组合，即便为拉格朗日所提及的带有棱角的方波函数亦满足该结论。

狄利克雷条件具体内容如下：

(1) 函数在任意有限区间内连续，或仅存在有限个第一类间断点；

(2) 函数在一个周期内，仅存在有限个极大值点与极小值点；

(3) 函数 x ( t ) x(t) x(t) 满足绝对可积条件，即 ∫ 0 ∞ ∣ x ( t ) ∣ d t < ∞ \int_{0}^{\infty}\left| x(t) \right|\mathrm{d}t<\infty ∫0∞∣x(t)∣dt<∞。

当函数满足狄利克雷条件时，其傅里叶变换及其逆变换的表达式为：

F ( ω ) = ∫ − ∞ + ∞ f ( t ) e − i ω t d t , f ( t ) = 1 2 π ∫ − ∞ + ∞ F ( ω ) e i ω t d ω . \begin{align*} F(\omega) &= \int_{-\infty}^{+\infty}f(t)e^{-i\omega t}\mathrm{d}t, \\[1em] f(t) &= \frac{1}{2\pi}\int_{-\infty}^{+\infty}F(\omega)e^{i\omega t}\mathrm{d}\omega. \end{align*} F(ω)f(t)=∫−∞+∞f(t)e−iωtdt,=2π1∫−∞+∞F(ω)eiωtdω.

据此可对拉格朗日与傅里叶的学术争议进行阐释：拉格朗日的观点具有数学严谨性，正弦曲线的线性组合无法精确表示带有棱角的信号，信号的棱角处会出现高频振荡现象，该现象被命名为吉布斯现象；而傅里叶的观点具有工程实用性，可通过正弦曲线的线性组合对带棱角的信号进行高精度逼近，逼近后的信号与原信号之间不存在能量差异。二者的观点差异源于研究视角的不同------拉格朗日从纯数学视角分析，傅里叶从工程应用视角分析。

三、 拉普拉斯变换的数学本质与物理内涵

傅里叶变换在工程领域得到了广泛应用，该变换为工程问题的求解提供了新的数学视角，基于该视角可简化诸多复杂问题的分析过程。傅里叶变换存在显著的应用局限性，即被变换的信号必须满足狄利克雷条件，其中绝对可积条件排除了大量不满足该条件的函数，例如函数 f ( t ) = t 2 f(t)=t^2 f(t)=t2 无法直接进行傅里叶变换。

针对这一局限性，数学家提出了对应的解决方法：将不满足绝对可积条件的函数与快速衰减的指数函数相乘，使乘积函数在自变量趋于 ∞ \infty ∞ 时收敛至 0，从而满足绝对可积条件。

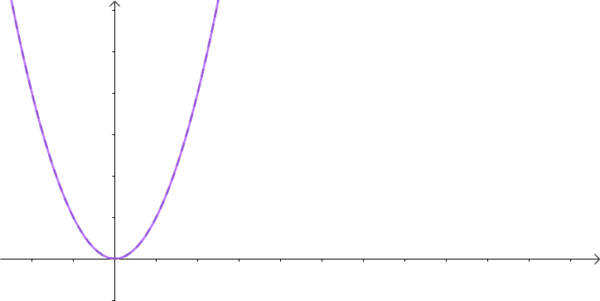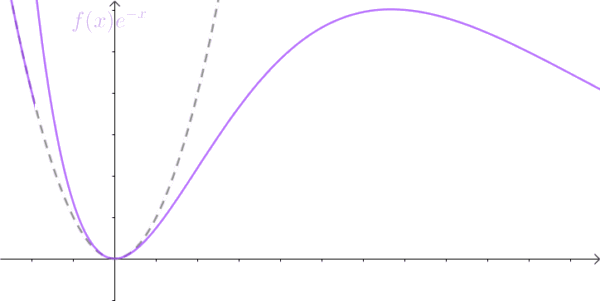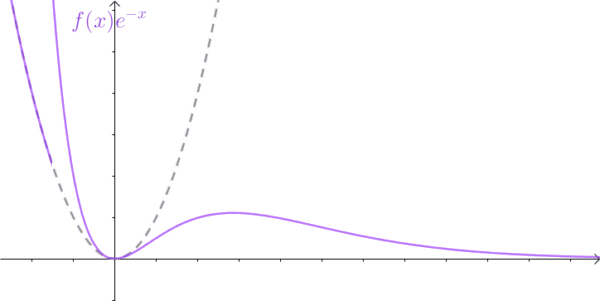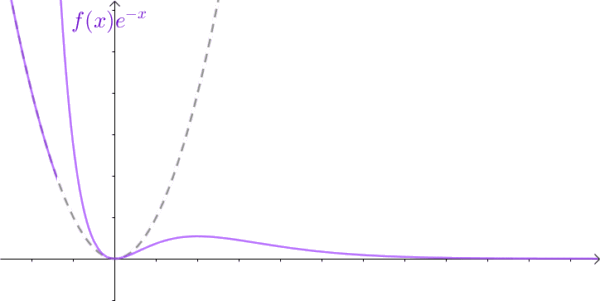
该方法的数学描述为：
lim ⁡ t → + ∞ f ( t ) e − σ t = 0 , σ ∈ R \lim_{t \rightarrow +\infty}f(t)e^{-\sigma t}=0,\ \sigma\in \mathbb{R} t→+∞limf(t)e−σt=0, σ∈R

为保证指数函数 e − σ t e^{-\sigma t} e−σt 为衰减函数，将自变量 t t t 的定义域限定为正半轴，此时可对原函数进行修正后的傅里叶变换，其表达式为：
F ( ω ) = ∫ 0 + ∞ f ( t ) e − σ t e − i ω t d t = ∫ 0 + ∞ f ( t ) e − ( σ + i ω ) t d t F(\omega)=\int_{0}^{+\infty}f(t)e^{-\sigma t}e^{-i\omega t}\mathrm{d}t=\int_{0}^{+\infty}f(t)e^{-(\sigma+i\omega) t}\mathrm{d}t F(ω)=∫0+∞f(t)e−σte−iωtdt=∫0+∞f(t)e−(σ+iω)tdt

令复变量 s = σ + i ω s=\sigma+i\omega s=σ+iω，则可得到如下表达式：
F ( s ) = ∫ 0 + ∞ f ( t ) e − s t d t F(s)=\int_{0}^{+\infty}f(t)e^{-st}\mathrm{d}t F(s)=∫0+∞f(t)e−stdt

该表达式即为拉普拉斯变换的数学定义。

针对拉普拉斯变换的数学推导，本文进一步从直观的几何视角进行阐释，以更清晰地展现其数学内涵。前文已提及，复指数函数 e − i ω t e^{-i\omega t} e−iωt 在复平面中对应不同角频率的旋转单位圆，若引入时间轴构建三维坐标系，复指数函数 e − i ω t e^{-i\omega t} e−iωt 对应的几何图形为螺旋曲线。

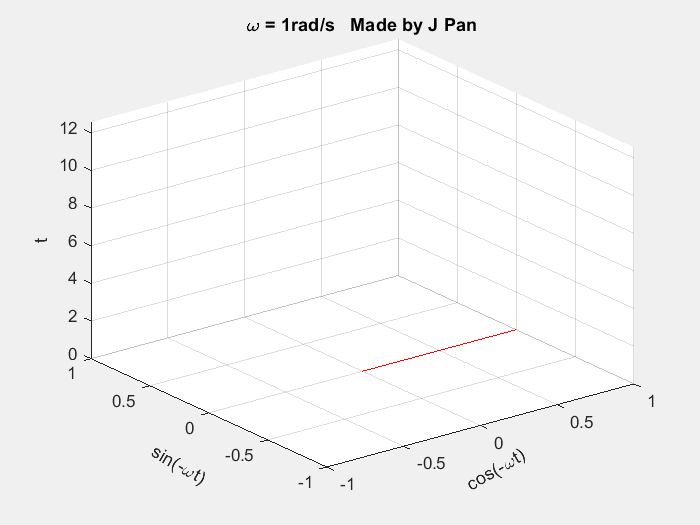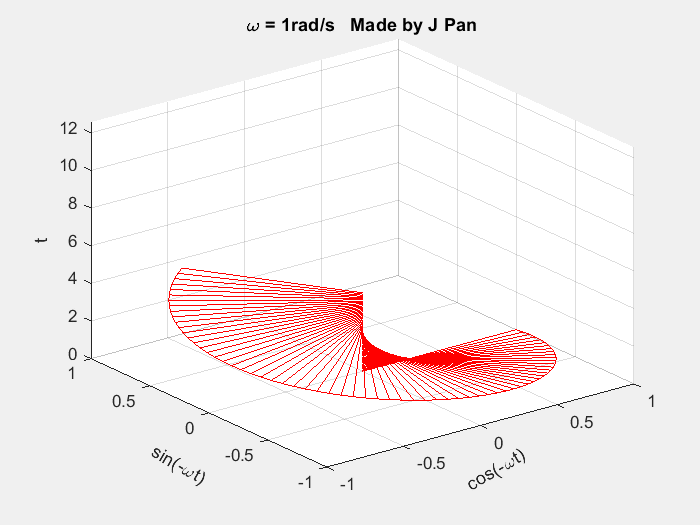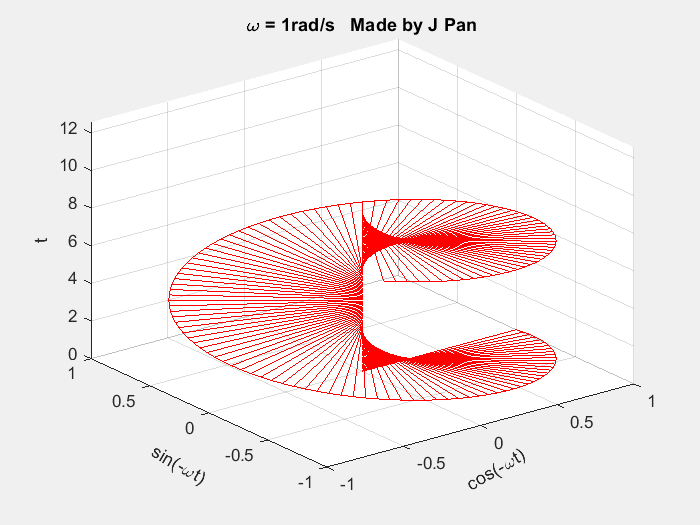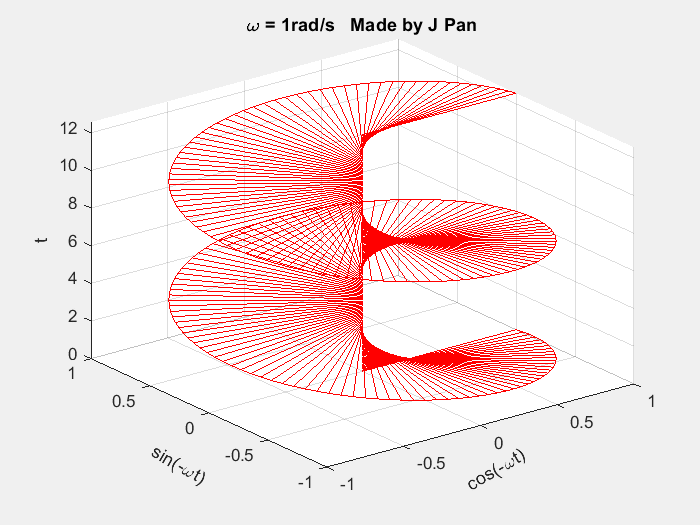
matlab 复制代码 
clc;clear;
h = animatedline;
h1=gcf;
view(3);
xl=xlabel('cos(-\omega t)');%
yl=ylabel('sin(-\omega t)');%
zl=zlabel('t');%
set(xl,'Rotation',30);%
set(yl,'Rotation',-30);%
grid on;
title('\omega = 1\mathrm{rad/s}   Made by J Pan')
axis([-1,1,-1,1,0,4*pi])
N = 200;
t=linspace(0,4*pi,N);
w=1;
x=cos(-w*t);
y=sin(-w*t);
a = tic; % start timer
for k = 1:N
    addpoints(h,x(k),y(k),t(k));
    hold on
    line([0 x(k)],[0 y(k)],[t(k) t(k)],'Color','red')
    b = toc(a); % check timer
    if b > (1/90)
        drawnow % update screen every 1/30 seconds
        a = tic; % reset timer after updating
    end
end

从三维坐标系的不同投影平面观察，该螺旋曲线的投影为正弦曲线或余弦曲线。

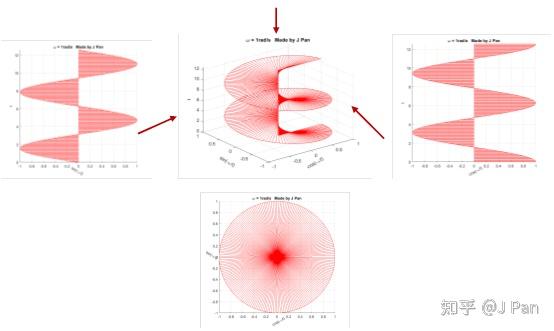
接下来对复指数函数 e − s t （ s = σ + i ω ） e^{-st}（s=\sigma+i\omega） e−st（s=σ+iω） 的几何特征进行分析：

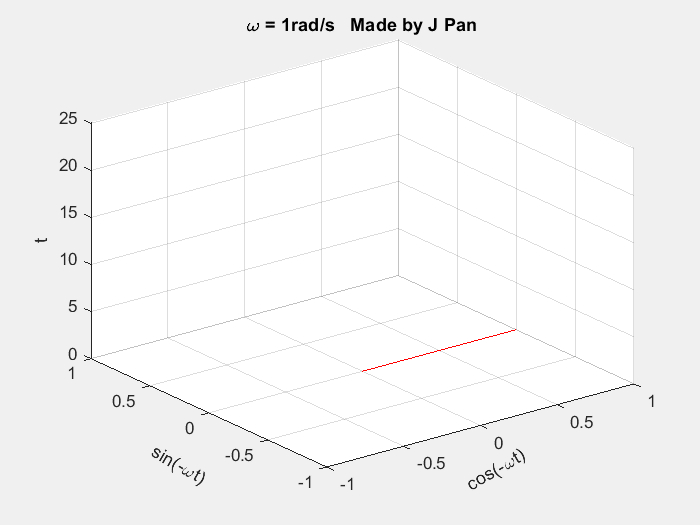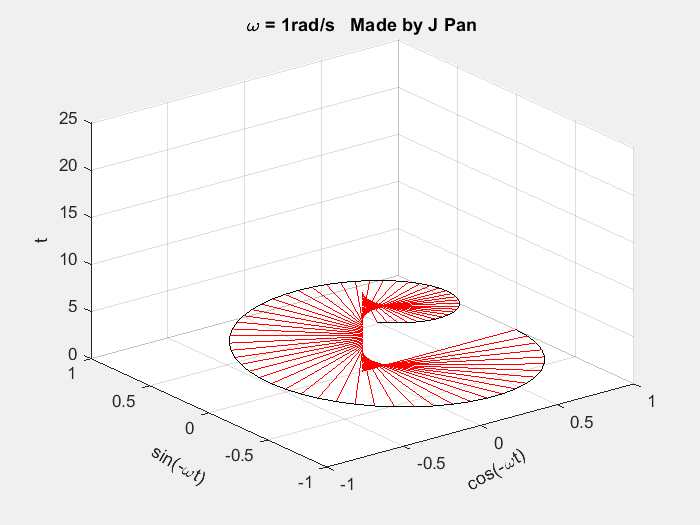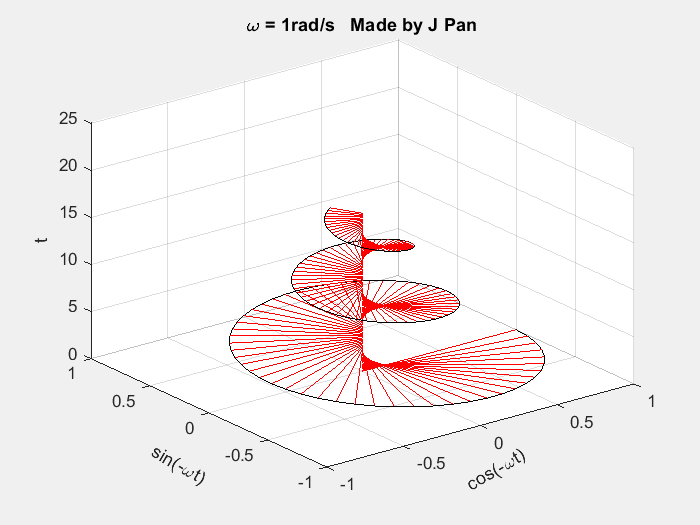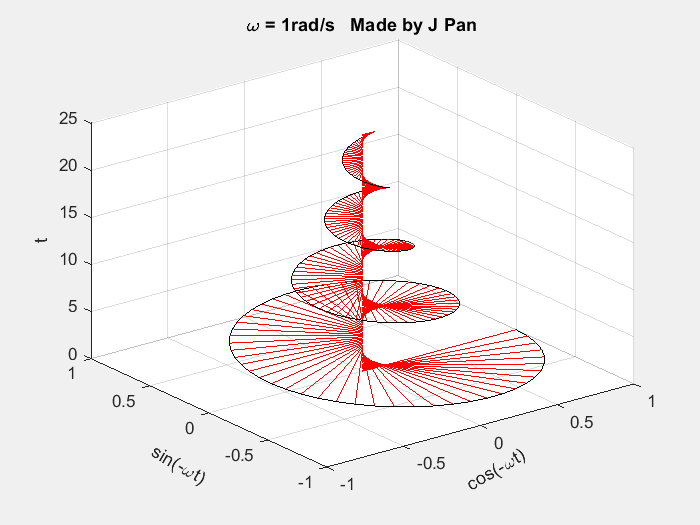
matlab 复制代码 
clc;clear;
h = animatedline;
h1=gcf;
view(3);
xl=xlabel('cos(-\omega t)');%
yl=ylabel('sin(-\omega t)');%
zl=zlabel('t');%
set(xl,'Rotation',30);%
set(yl,'Rotation',-30);%
grid on;
title('\omega = 1\mathrm{rad/s}   Made by J Pan')
axis([-1,1,-1,1,0,4*pi])
N = 200;
t=linspace(0,4*pi,N);
w=1;sig=0.1;
x=exp(-sig*t).*cos(-w*t);
y=exp(-sig*t).*sin(-w*t);
a = tic; % start timer
for k = 1:N
    addpoints(h,x(k),y(k),t(k));
    hold on
    line([0 x(k)],[0 y(k)],[t(k) t(k)],'Color','red')
    b = toc(a); % check timer
    if b > (1/90)
        drawnow % update screen every 1/30 seconds
        a = tic; % reset timer after updating
    end
end

复指数函数 e − s t e^{-st} e−st 为螺旋曲线与衰减指数函数的乘积，其对应的几何图形为半径随时间不断减小的螺旋曲线。该曲线在不同投影平面的几何特征为：投影为衰减的正弦曲线或余弦曲线；在复平面的投影为半径不断减小的圆。


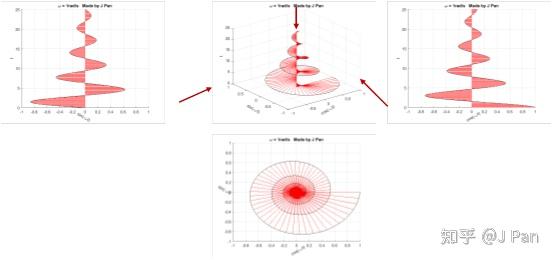
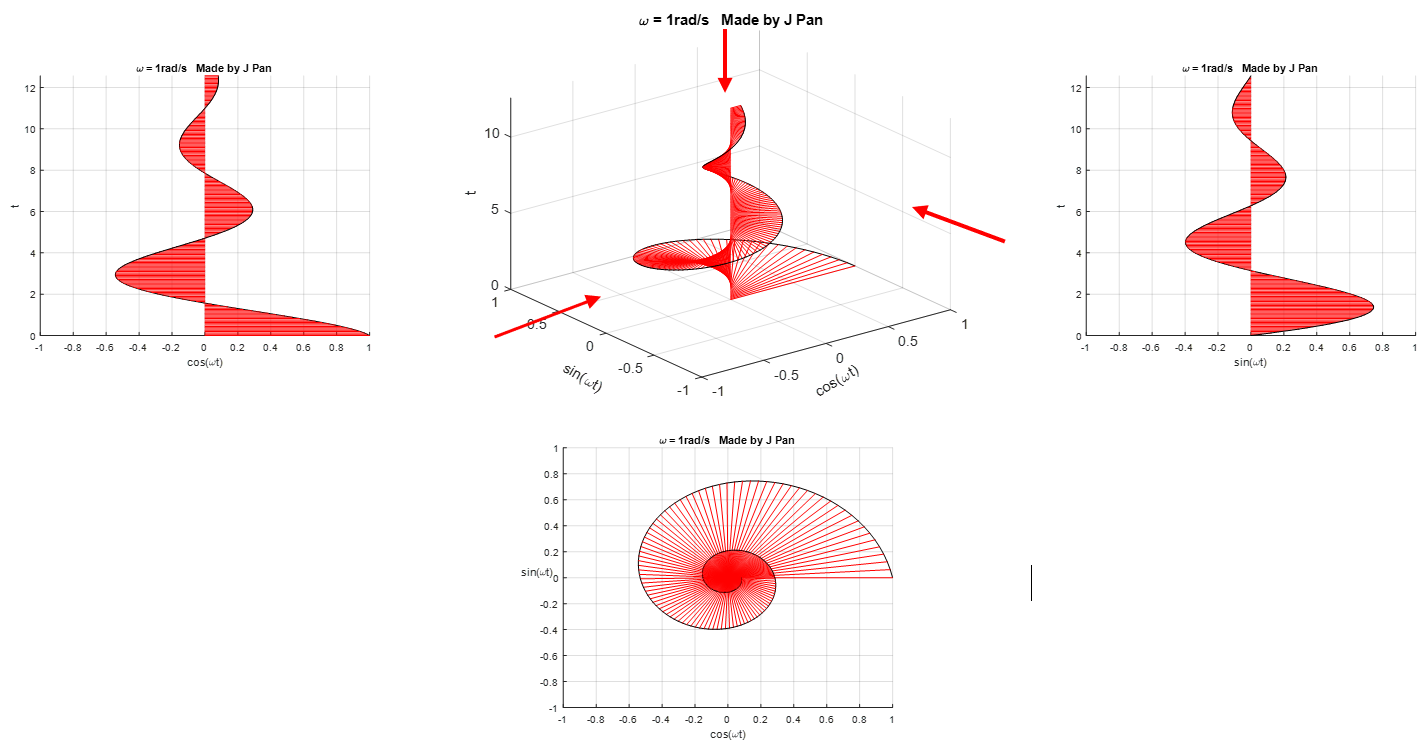
综上可得：傅里叶变换是将函数分解为复平面中角频率不同、幅值恒为 1 的单位圆的线性组合；拉普拉斯变换是将函数分解为复平面中角频率与幅值均可变的圆的线性组合。拉普拉斯变换的基函数包含两个独立变量，因此其数学形式更具灵活性，应用范围也更为广泛。

拉普拉斯变换与赫维赛德微积分算子的数学关联可通过如下推导清晰展现，这也是微分算子成为拉普拉斯变换前身的原因：

对于微分运算，有：
d d t ( e s t ) = s e s t \frac{\mathrm{d}}{\mathrm{d}t}(e^{st})=se^{st} dtd(est)=sest

令 f ( t ) = e s t f(t)=e^{st} f(t)=est，则有：
d f ( t ) d t = s ⋅ f ( t ) \frac{\mathrm{d}f(t)}{\mathrm{d}t}=s\cdot f(t) dtdf(t)=s⋅f(t)

对于积分运算，有：
∫ − ∞ t e s τ d τ = 1 s e s t \int_{-\infty}^{t}e^{s\tau}\mathrm{d}\tau=\frac{1}{s}e^{st} ∫−∞tesτdτ=s1est

令 f ( t ) = e s t f(t)=e^{st} f(t)=est，则有：
∫ − ∞ t f ( τ ) d τ = 1 s f ( t ) \int_{-\infty}^{t}f(\tau)\mathrm{d}\tau=\frac{1}{s}f(t) ∫−∞tf(τ)dτ=s1f(t)

该推导结果与赫维赛德微积分算子的数学形式高度一致。

via:

热门推荐
01GitHub 镜像站点02Clawdbot 中文汉化版 接入微信、飞书03OpenClaw部署与配置教程：在Mac mini上接入国产大模型与飞书042026美赛A题智能手机电池续航时间预测的连续时间数学模型05OpenCode 入门教程：介绍 · 安装 · 配置第三方 API (如 Claude)06UV安装并设置国内源07Linux下V2Ray安装配置指南082025 年大语言模型发展回顾：关键突破、意外转折与 2026 年展望09Claude Code + GLM4.7 避坑指南：解决 Unable to connect to Anthropic services10【Milvus】向量数据库pymilvus使用教程