【初阶数据结构-二叉树】

文章目录

二叉树
一、堆的基本概念
- [1. 堆](#1. 堆)
- 2.堆的实现
- - 2.1堆的向上调整算法
  - - [2.1.1 向上调整算法的时间复杂度](#2.1.1 向上调整算法的时间复杂度)
    - [2.1.2 堆的插入](#2.1.2 堆的插入)
  - [2.2 向下调整算法](#2.2 向下调整算法)
  - - 2.2.1向下调整图解
    - [2.2.2 计算向下调整算法的时间复杂度](#2.2.2 计算向下调整算法的时间复杂度)
- [3. 堆排序](#3. 堆排序)

二叉树

上一章我们了解了树的基本概念以及二叉树的形式，本章我们继续用堆来实现二叉树

一、堆的基本概念

一般堆使用顺序结构的数组来实现二叉树，堆是一种特殊的二叉树，具备二叉树特性的同时还具备了一些其他的特性

1. 堆

如果有一个关键码的集合K{ k 0 k_0 k0, k 1 k_1 k1, k 2 k_2 k2...， k i k_i ki}，用二叉树顺序存储的方式，以一维数组的形式存储，满足 k 2 ∗ i + 1 k_{2*i+1} k2∗i+1（ k 2 ∗ i + 2 k_{2*i+2} k2∗i+2）<= k i k_i ki,即孩子小等于父亲，这就是大堆；反之，即小堆；（i=0,1,2......）将根节点最大的点叫做最大堆获大根堆，根节点最小的堆就是最小堆或者小根堆；

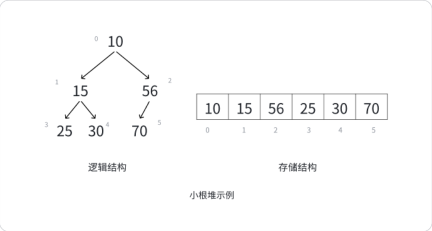
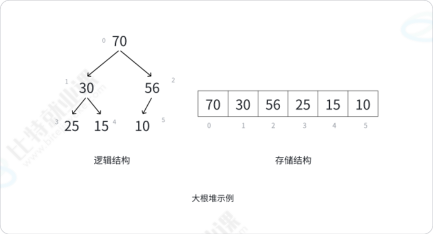
堆具有一下的性质

堆中的某个节点总是不大于或者不小于其父节点；

堆总是一颗完全二叉树
完全二叉树的性质

对于一个具有n个节点的二叉树来说，从上至下从左至右的数组顺序对所有结点从0开始编号，则对于序号i:

对于序号i>0（左孩子或者右孩子），他的父亲节点是（i-1）/2;当i=0时，没有父亲节点

若2i+1<n,则左孩子序号：2i+1.当2I+1>n时，左孩子不存在；

若2i+2<n,则右孩子序号：2i+2.当2I+2>n时，右孩子不存在；

2.堆的实现

堆的实质上是一个一维数组，先构建起一个结构体，记录数组的现存大小和整体大小，基础实现接口如下：

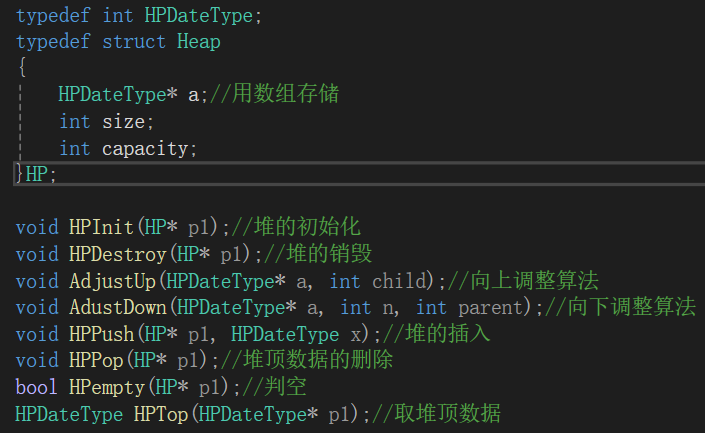
c 复制代码

void HPInit(HP* p1)
{
	assert(p1);
	p1->a = NULL;
	p1->size = p1->capacity = 0;
}
void HPDestroy(HP* p1)
{
	assert(p1);
	free(p1->a);
	p1->a = NULL;
	p1->size = p1->capacity = 0;
}
void Swap(HPDateType* p1, HPDateType* p2)
{
	HPDateType tmp;
	tmp = *p1; *p1 = *p2; *p2 = tmp;
 }
 bool HPempty(HP* p1)
{
	assert(p1);
	return p1->size == 0;
}
HPDateType HPTop(HPDateType* a)
{
	assert(a);
	return a[0];
}

2.1堆的向上调整算法

在堆的插入过程中，一直在数组尾部插入是满足不了堆的要求的；在这里可以用到向上调整算法，数组尾部插入一个向上调整一次，这样最后可以满足一个大堆或者小堆；

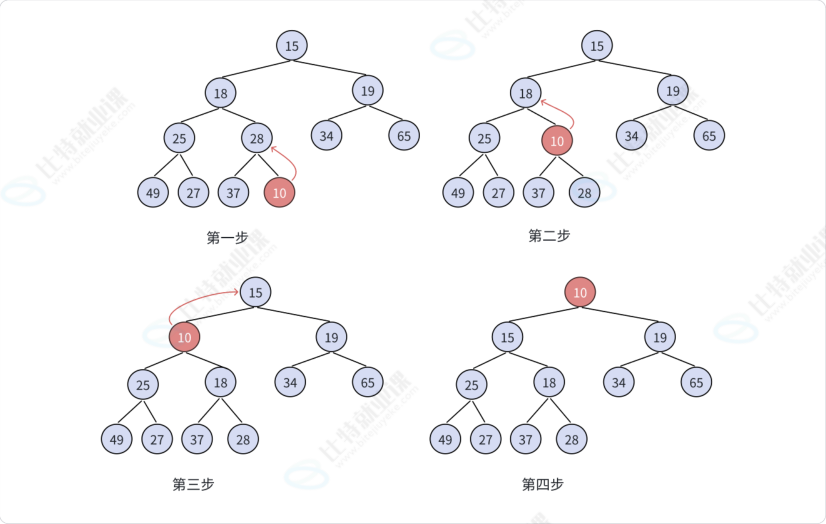
实质就是调小堆，孩子比父亲小就交换向上调整，谁小谁向上调；

调大堆，孩子比父亲大就交换向上调整，谁大向上调整；

c 复制代码

void AdjustUp(HPDateType* a, int child)
{
	int parent = (child - 1) / 2;
	//调小堆，谁小谁向上调
	//调大堆，谁大谁向上调
	while (child > 0)
	{
		if (a[child] > a[parent])
		{
			Swap(&a[child], &a[parent]);
			child = parent;
			parent = (child - 1) / 2;
		}
		else
		{
			break;
		}
	}
}

堆的插入

c 复制代码

void HPPush(HP* p1, HPDateType x)
{
	assert(p1);
	//判断空间是否足够
	if (p1->size == p1->capacity)
	{
		int newcapacity = p1->size == 0 ? 4 : p1->capacity * 2;
		HPDateType* tmp = (HPDateType*)realloc(p1->a, newcapacity * sizeof(HPDateType));
		if (tmp == NULL)
		{
			perror("relloc fail");
			exit(1);
		}
		p1->a = tmp;
	}
	p1->a[p1->size] = x;
	p1->size++;
	//调整成堆
	//向上调整算法
	AdjustUp(p1->a, p1->size - 1);
}

2.1.1 向上调整算法的时间复杂度

因为堆是一个完全二叉树，而满二叉树也是一个完全二叉树，这里为了简化问题好计算，我们用满二叉树来证明（时间复杂度算的是一个近似值，一个量级，所以对几个节点不影响最后的结果）

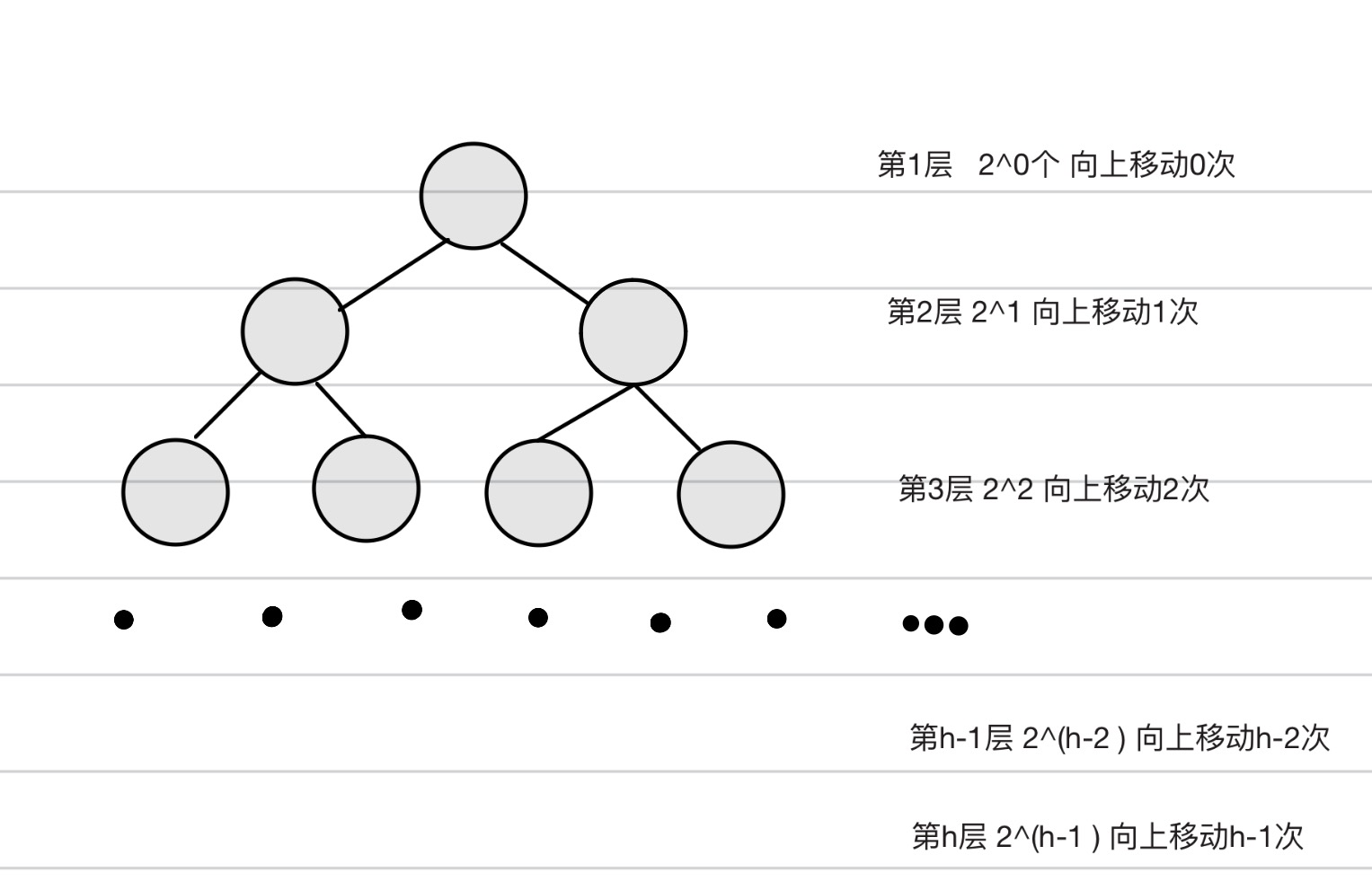
由此可得向上调整算法的时间复杂度是O(N* l o g 2 N log_2N log2N)

2.1.2 堆的插入

c 复制代码

void AdjustUp(HPDateType* a, int child)
{
	int parent = (child - 1) / 2;
	while (child > 0)
	{
		if (a[child] > a[parent])//调大堆
		{
			Swap(&a[child], &a[parent]);
			child = parent;
			parent = (child - 1) / 2;
		}
		else
		{
			break;
		}
	}
}
void HPPush(HP* p1, HPDateType x)
{
	assert(p1);
	//判断空间是否足够
	if (p1->size == p1->capacity)
	{
		int newcapacity = p1->size == 0 ? 4 : p1->capacity * 2;
		HPDateType* tmp = (HPDateType*)realloc(p1->a, newcapacity * sizeof(HPDateType));
		if (tmp == NULL)
		{
			perror("relloc fail");
			exit(1);
		}
		p1->a = tmp;
	}
	p1->a[p1->size] = x;
	p1->size++;
	//调整成堆
	//向上调整算法
	AdjustUp(p1->a, p1->size - 1);
}

2.2 向下调整算法

当进行堆的删除是，一搬不会说把堆底元素给删除，这样毫无挑战性，删完堆的性质不变；我们要做的是把堆顶元素删除。方法是将堆顶元素和堆底元素交换，交换完后删除，在进行向下调整

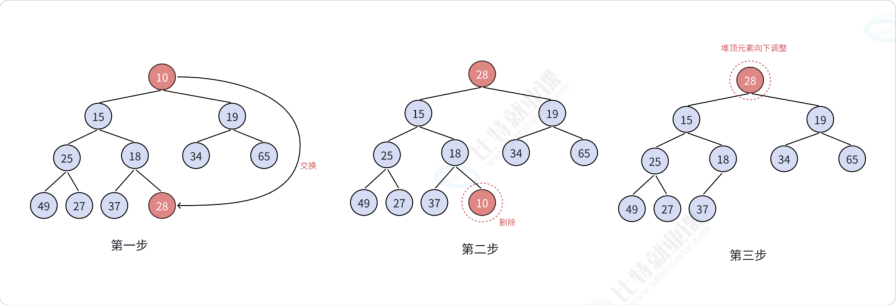
2.2.1向下调整图解

向下调整算法有个前提：左右子树必须都是一个堆，才能进行调整

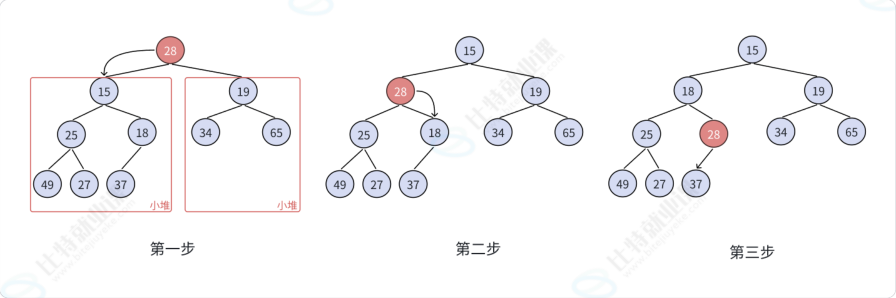
向下调整算法

将堆顶元素和堆中最后一个元素交换

删除堆中最后一个元素

将堆顶元素进行向下调整建堆，直到满足堆的特性为止

c 复制代码

void AdustDown(HPDateType* a, int n, int parent)
{
//调整大堆
//假设法 假设左孩子大
	int child = parent * 2 + 1;
	while (child <n)
	{
	//如果比较过后右孩子小，在进行调换
		if (child + 1<n&&a[child] < a[child + 1])
		{
			child = child + 1;
		}
		if (a[child] >a[parent])
		{
			Swap(&a[child], &a[parent]);
			 parent=child;
			 child = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}
//删除的是堆顶部的数据
void HPPop(HP* p1)
{
	assert(p1);
	assert(p1->size > 0);
	//交换后删除
	Swap(&p1->a[0], &p1->a[p1->size - 1]);
	p1->size--;
	//向下调整
	AdustDown(p1->a, p1->size, 0);
}

2.2.2 计算向下调整算法的时间复杂度

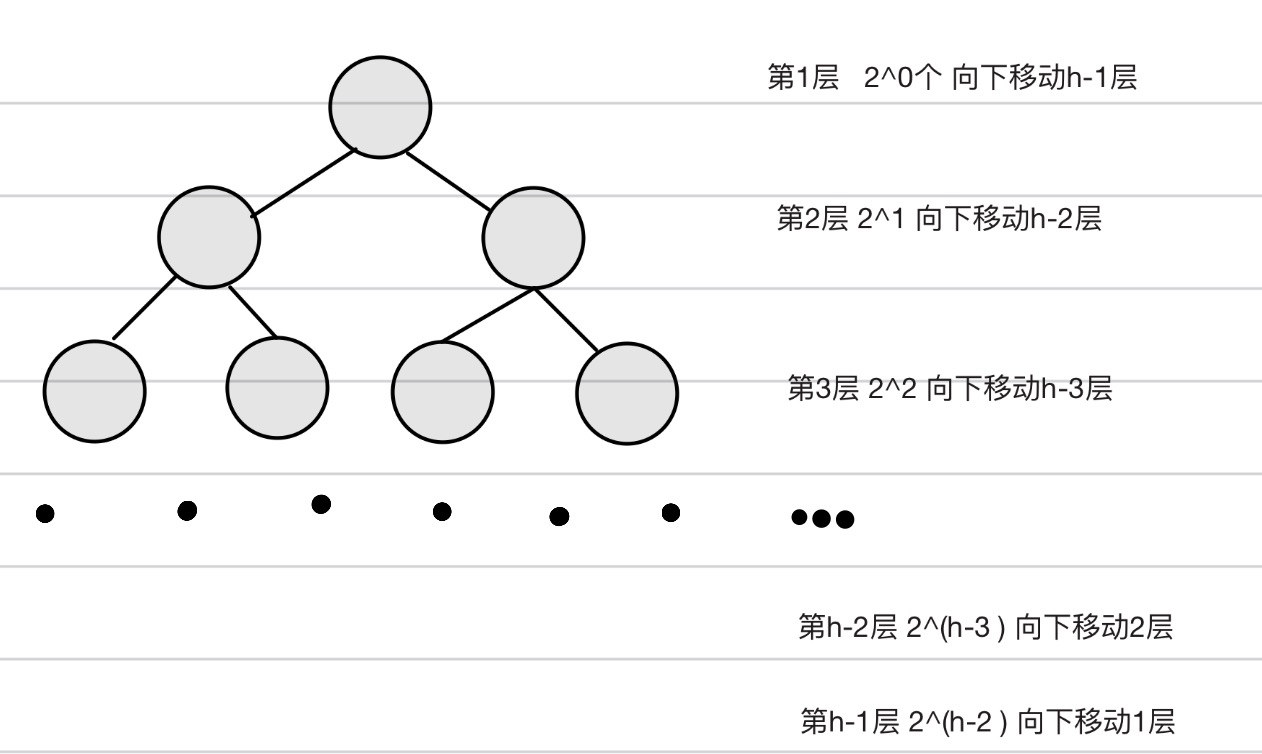
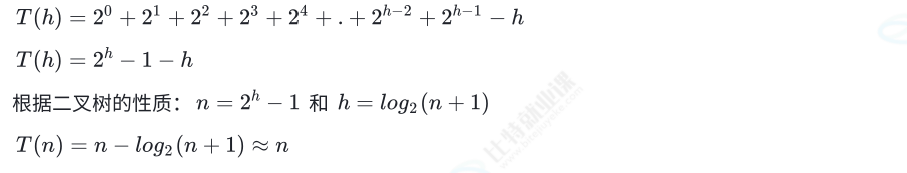
由此可知向下调整算法的时间复杂度是O(N)

所以我们经常将向下调整算法当作第一选择来使用

3. 堆排序

堆排序即利用堆的思想来进行排序，总共分为两个步骤：

建堆

升序：建大堆
降序：建小堆

利用堆删除的思想来进行排序（堆顶堆低数据交换，删除堆低）

建堆和堆删除都用到了向下调整算法，因此掌握了向下调整算法就可以完成堆排序

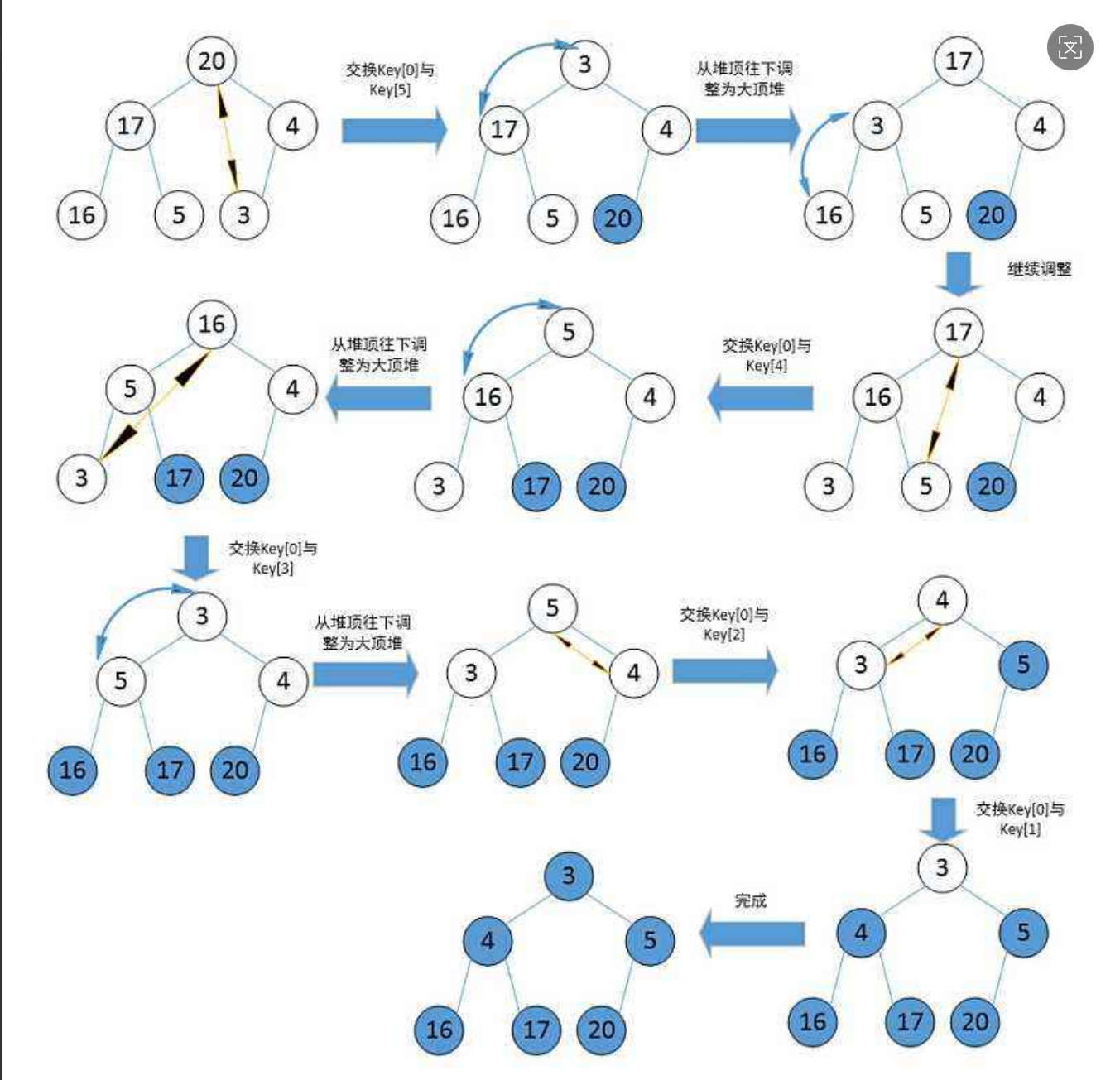
第一步，建堆

给你一个乱序数组怎么将他变成一个大堆或者小堆，由上述关于时间复杂度的分析，向下调整算法的时间复杂度最优，所以建堆时我们采用向下调整算法；

向下调整算法的前提条件就是左右支都满足堆，所以我们采用从下往上一次进行调整，即从倒数第一个非叶子节点开始

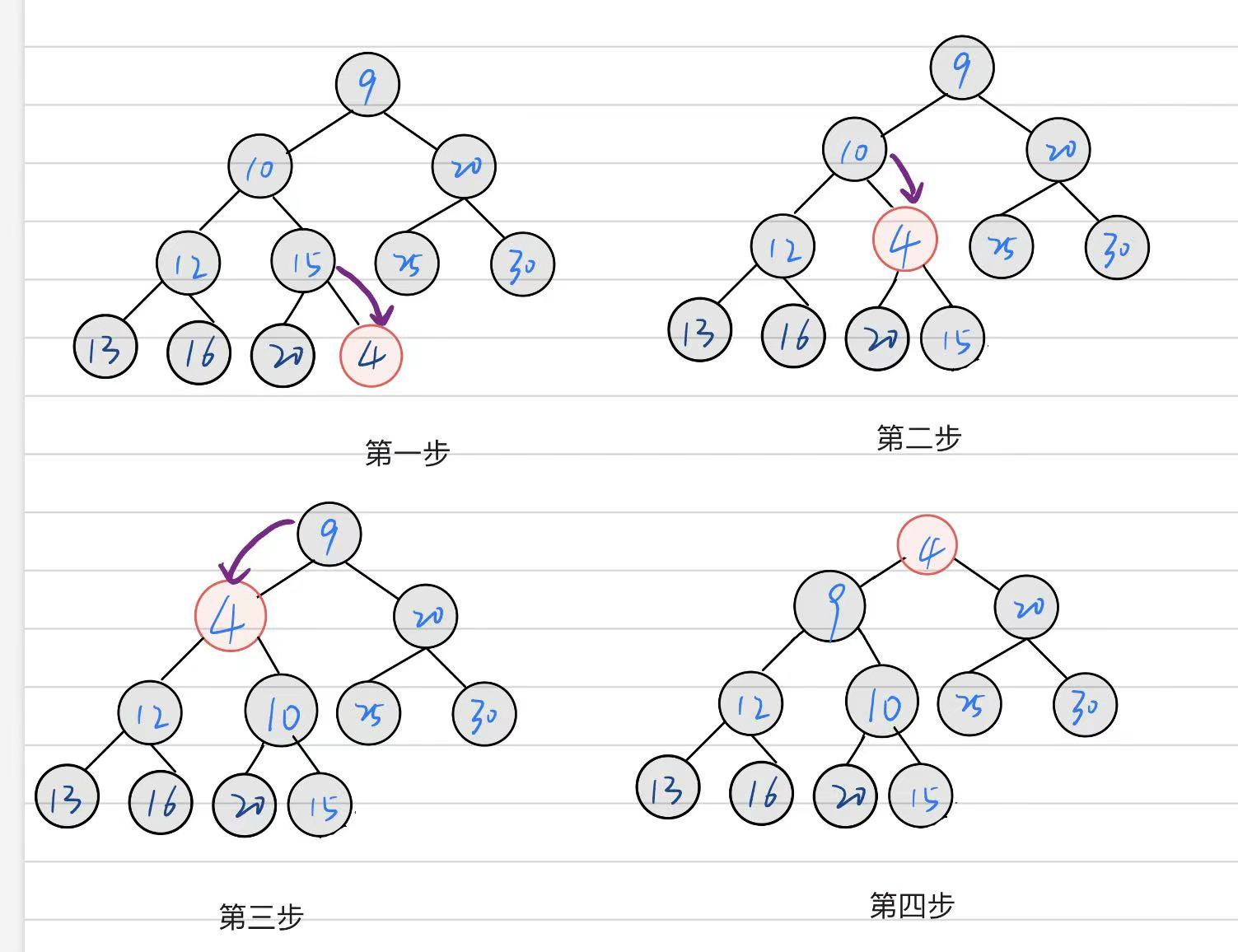
c 复制代码

#include "stdio.h"
//传数组和数组元素个数和父亲节点
void CreatHeat(int* a,int n，int parent)
{
//假如建大堆
for(int i=(n-1-1)/2;i>=0;i--)
{
	Adustdown(a,n,i);
}
}

第二步，交换并删除，即用 HPPop的思想，此时堆排序的整体代码(假设升序)：

c 复制代码

void HeatSort(int a,int n)
{
	for(int i=(n-1-1)/2;i>=0;i--)
	{
		Adustdown(a,n,i);
	}
	int end=n-1;
	while(end)
	{
		Swap(&a[0],&a[end]);
		Adustdown(a,end,0);
		--end;
	}
}

小结：本章用堆实现了二叉树的顺序存储，向上调整以及向下调整算法的具体分析，又用堆实现了排序；相信你对二叉树的理解有进步了一分

下章预告：

😊实现TopK问题

😊用链表实现二叉树

🙌二叉树的前中后序遍历