回文自动机 PAM 学习笔记

回文自动机

zeb 于 2026.2.2 讲解，做一个笔记。

1. 引入

回文树，或者说，回文自动机 PAM（Palindromic Automaton），是一种可以存储一个串中所有本质不同回文子串的数据结构。

由于这个算法就是从其它字符串相关自动机借鉴而来，因此于其它自动机有许多相似之处。在这个回文自动机中，每一个状态（即节点）都对应了原串中的一个子串。而不同的是，转移边上的字符，指的是在原状态上两侧分别加上一个这个字符，所形成的回文子串。

例如

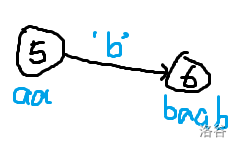
你就会发现一个问题，我们这样只能得到偶数长度的子串，那该怎么办呢？也像 \(\text{Manacher}\) 那样加入间隔字符？

我们考虑一个巧妙而快捷的方法------我们建两棵根，一个是奇根 ，下面挂所有长度为奇数的回文子串；一个是偶根，下面挂所有长度为偶数的回文子串。

2. 构造

对每个状态，我们会储存以下内容：

• 对应字符串长度 \(\mathtt{len_u}\)；
• 对应字符串所有出边指向的结点 \(\mathtt{trie_{u,c}}\)；
• 状态的失配指针 \(\mathtt{fail_u}\)（含义在下文）。

对于奇根和偶根，我们分别定义它们的长度为 \(-1\) 和 \(0\)。这样可以保持统一性，在一个状态后加入一个后继状态时，它所对应的长度就直接设为它父亲长度加 \(2\) 即可。

对于 \(\text{PAM}\) 的构造，我们类似于 \(\text{SAM}\) 采用增量构造，即每加入一个字符，我们都可以实时更新这个回文自动机。

那么，不妨设我们现在要加入的这个点是第 \(i\) 个字符，前 \(i-1\) 个字符对应的 \(\text{PAM}\) 已经构造好。

我们考虑加入这个字符串会产生的新的回文子串，即以第 \(i\) 位为结尾的回文子串。在这么多的回文子串中，我们每个都要新建节点吗？并非，事实上，我们只需要新建最长的一个后缀回文子串对应状态即可。因为可以保证，比它短的以前一定已经出现过了，比如说这个例子：

对于子串 \(\mathtt{abaccaba}\)，后缀回文子串共有三个，\(\mathtt{abaccaba,aba,a}\)。

其中你会发现，如果一个后缀回文子串不是最长的，那么它一定可以被最长的那一个后缀回文子串翻转过去 ，比如说这里的 \(\mathtt{aba}\)，就可以通过整个子串找到一个对称位置上同样的 \(\mathtt{aba}\)，这也就是为什么我们至多只需要新建最长回文后缀对应节点就可以了。

现在我们的任务，就是找到这个新节点该建立在哪里。你会发现，这个节点的父亲，即将这个最长回文后缀掐头去尾，一定也是一个回文串，且就是 \(i-1\) 位置上的一个后缀回文子串。于是这个任务就转化成了，找到一个对应子串最长的节点 \(u\) 满足

• 它对应的子串是 \(i-1\) 的一个后缀回文子串；
• \(s_{i-\mathtt{len_u}-1}=s_i\)。

我们记录 \(i-1\) 位置最长回文后缀对应状态节点编号为 \(\mathtt{last}\)。如果这个节点已经满足这个条件了，很好，我们直接把新节点连在 \(\mathtt{last}\) 下面即可。但如果不行呢？因此，我们这里类似 \(\text{ACAM}\)，引入 \(\text{Fail}\) 失配指针。\(\mathtt{fail_u}\) 表示的含义是，状态 \(u\) 对应的回文子串的最长回文后缀对应的状态。

那么可以发现，\(\mathtt{last},\mathtt{fail_{last}},\mathtt{fail_{fail_{last}}},\dots\) 就对应了以 \(i-1\) 结尾的所有后缀回文子串！

因此在这里，我们只需要不断往上跳 \(\text{Fail}\) 指针即可。那么如果一直找都找不到，怎么办？这时候我们考虑把偶根的 \(\mathtt{fail_0}\) 连到奇根上去。这样跳 \(\text{Fail}\) 时，由于奇根的 \(\mathtt{len_1}=-1\)，因此 \(i-\mathtt{len_1}-1=i\)，即对于 \(s_i\) 这个单字符的回文串，二条件一定成立，很自然的就会连到奇根下面。这一方面揭示了设奇根长度为 \(-1\) 的另一好处，同时也说明了，为什么 \(\mathtt{fail_0}\leftarrow 1\)。

那么找到了父亲，我们接下来就是要为这一点也连一条 \(\text{Fail}\) 指针出去。

其实也很简单，这条 \(\text{Fail}\) 指针，连向的其实就是以 \(i\) 结尾的第二长的回文后缀。那么我们只需要继续从 \(\mathtt{fail_{last}}\) 开始跳，再找到第一个符合二条件的就可以了。

下面是实现。

int last,tot=1,fail[N],len[N],trie[N][30];
//last 最开始挂在偶根
//tot 记得要赋初值为 1
int getfail(int u,int id){
    while(s[id]!=s[id-len[u]-1]) u=fail[u]; //不满足二条件就一直跳
    return u;
}
void pamConstruct(){
    fail[0]=1,len[1]=-1;
    //初始化 偶根的 fail 指向奇根，奇根的长度为 -1
    for(int i=1;i<=n;i++){
		int fa=getfail(last,i);
        //找到 i-1 的回文后缀中最长的那个符合二条件的，作为其父亲
		if(!trie[fa][s[i]-'a']){
			fail[++tot]=trie[getfail(fail[fa],i)][s[i]-'a'];
            //从 fail[fa] 开始，是因为我们找的是真后缀
			trie[fa][s[i]-'a']=tot;
            //先找 fail 再连边！！
			len[tot]=len[fa]+2;
		}
		last=trie[fa][s[i]-'a'];
	}
}

有关复杂度，首先，由代码也可以看出，状态最多只有 \(n\) 个，因此空间复杂度是 \(O(n\Sigma)\) 的。

时间复杂度，首先除了跳 \(\text{Fail}\) 都是 \(O(n)\) 的。

每次跳 \(\text{Fail}\) 时，每一条 Fail 边至多被经过一次，而增添 \(\text{Fail}\) 指针时，最多新添一条 Fail 边。因此跳 \(\text{Fail}\) 的次数至多就是 \(O(n)\) 的，因此总时间复杂度是 \(O(n)\)。

3. 应用

求以某位置结尾的回文子串个数，强制在线

即 P5496，分析一下，其实就是它在 Fail 树上的深度嘛。

代码

const int N=5e5+10;
string s;
int n,lastans;
int last,tot=1,fail[N],len[N],trie[N][30];
int dep[N];
int getfail(int u,int id){
	while(s[id]!=s[id-len[u]-1]) u=fail[u];
	return u;
}
int main(){
	ios::sync_with_stdio(false);
	cin.tie(0);cout.tie(0);
	cin>>s; n=s.length();
	s=" "+s;
	fail[0]=1,len[1]=-1;
	for(int i=1;i<=n;i++){
		s[i]=(s[i]-97+lastans)%26+97;
		int fa=getfail(last,i);
		if(!trie[fa][s[i]-'a']){
			fail[++tot]=trie[getfail(fail[fa],i)][s[i]-'a'];
			trie[fa][s[i]-'a']=tot;
			len[tot]=len[fa]+2;
			dep[tot]=dep[fail[tot]]+1;
		}
		last=trie[fa][s[i]-'a'];
		lastans=dep[last];
		cout<<lastans<<" ";
	}
	cout<<"\n";
	return 0;
}

求某个回文子串的出现次数

你会发现在 Fail 树上，一个状态的后代所对应的子串全都包含它。因此我们记录 \(\mathtt{cnt_u}\) 表示 \(u\) 状态在构建时被抵达了多少次，最后一个节点答案就应该是子树和。

P3649 代码如下

const int N=3e5+10;
string s;
int n;
ll ans;
int tot=1,last,len[N],siz[N],fail[N],trie[N][30];
vector<int> T[N];
int getfail(int u,int id){
	while(s[id]!=s[id-len[u]-1]) u=fail[u];
	return u;
}
void dfs(int u){
	for(auto v:T[u]) dfs(v),siz[u]+=siz[v];
	ans=max(ans,1ll*len[u]*siz[u]);
}
int main(){
	ios::sync_with_stdio(false);
	cin.tie(0);cout.tie(0);
	cin>>s; n=s.length();
	s=" "+s;
	len[1]=-1,fail[0]=1;
	T[1].push_back(0);
	for(int i=1;i<=n;i++){
		int fa=getfail(last,i);
		if(!trie[fa][s[i]-'a']){
			fail[++tot]=trie[getfail(fail[fa],i)][s[i]-'a'];
			T[fail[tot]].push_back(tot);
			trie[fa][s[i]-'a']=tot;
			len[tot]=len[fa]+2;
		}
		last=trie[fa][s[i]-'a'];
		siz[last]++;
	}
	dfs(1);
	cout<<ans<<"\n";
	return 0;
}

前端插入

是的，\(\text{PAM}\) 支持前端插入，这得益于回文串良好的对称性质。

假设我们要在位置 \(l\) 新增一个字符，我们就要找到 \(l+1\) 的最长回文前缀中，第一个合法的。那我们要额外建立另一颗 Fail 树吗？并不用，因为你会发现一个回文串的回文前缀，一定也是这个回文串的回文后缀，因此 Fail 完全可以共用。

唯一要改变的是，我们原先是一个 \(\mathtt{last}\)，在这里我们要用两个，\(\mathtt{pre}\) 和 \(\mathtt{suf}\)，分别表示 \(l\) 最长回文前缀对应的状态，和 \(r\) 最长回文后缀对应的状态。什么时候两者可能会相互影响呢？你会发现，只有当整个串都变成了一个回文串，两者就会相互影响了，此时要将它们统一设成最后一个状态。

HDU5421 代码如下。

const int N=2e5+10;
char s[N];
int q,L,R;
ll ans;
int tot,fail[N],trie[N][30],len[N],dep[N];
int pre,suf;
void init(){
	tot=1,ans=0;
	pre=0,suf=0;
	L=1e5+1,R=L-1;
	memset(fail,0,sizeof(fail));
	memset(trie,0,sizeof(trie));
	memset(len,0,sizeof(len));
	memset(dep,0,sizeof(dep));
	memset(s,0,sizeof(s));
	fail[0]=1,len[1]=-1;
}
int getfail(int u,int id,int op){
	while(s[id]!=s[id-op*(len[u]+1)]) u=fail[u];
	return u;
}
void insert(char c,int pos,int &last,int op){
	int fa=getfail(last,pos,op);
	if(!trie[fa][c-'a']){
		fail[++tot]=trie[getfail(fail[fa],pos,op)][c-'a'];
		trie[fa][c-'a']=tot;
		len[tot]=len[fa]+2,dep[tot]=dep[fail[tot]]+1;
	}
	last=trie[fa][c-'a'];
	ans+=dep[last];
	if(len[last]==R-L+1) pre=suf=last;
}
int main(){
	ios::sync_with_stdio(false);
	cin.tie(0);cout.tie(0);
	while(cin>>q){
		init();
		while(q--){
			int op; char c;
			cin>>op;
			if(op==1){
				cin>>c; s[--L]=c;
				insert(c,L,pre,-1);
			}
			else if(op==2){
				cin>>c; s[++R]=c;
				insert(c,R,suf,1);
			}
			else if(op==3) cout<<tot-1<<"\n";
			else cout<<ans<<"\n";
		}
	}
	return 0;
}

回文自动机上 dp

一道例题：P4762 Virus synthesis

初始有一个空串，利用下面的操作构造定串 \(S\)。

• 串开头或末尾添加一个字符；
• 翻转字符串，添加到在开头或末尾。

求最小的操作数，\(|S|\le 10^5\)，字符集为 \(\{A,T,C,G \}\)。

可以先去玩一下样例。

二操作是一个很好的东西，它可以减省很多时间。因此，我们考虑最后一次使用二操作 所形成的字符串，设其所需操作次数为 \(f(T)\)，那么剩下的暴力操作非常好计算，总次数就是 \(n-|T|+f(T)\)，在所有偶回文子串中选一个最小的就可以了，这些回文子串都可以在 \(\text{PAM}\) 上存储。问题转化为如何计算一个偶回文子串的最小操作次数。

首先对于这个偶回文子串，最后一步一定是翻转，没的说。考虑怎么转移来。

• 从同心的回文子串转移来：即从其在 \(\text{PAM}\) 上的父亲的操作次数加一，\(f(\mathtt{fa_u})+1\)；
• 从不同心的回文子串转移来：我们跳 Fail 链，找到第一个 \(\mathtt{len}\) 值小于等于当前串一半的，设这个为 \(\mathtt{trans_u}\)，答案就是 \(f(\mathtt{trans_u})+\dfrac {\mathtt{len_u}}{2}-\mathtt{len_{trans_u}}+1\)。

求 \(\mathtt{trans}\) 的方法与 Fail 树类似。时间复杂度 \(O(n)\)。

const int N=1e5+10;
string s;
int n;
int tot,trie[N][4],len[N],fail[N];
int trans[N];
int dp[N];
int last;
int getid(char c){
	if(c=='A') return 0;
	else if(c=='G') return 1;
	else if(c=='C') return 2;
	else return 3;
}
int getfail(int u,int id){
	while(s[id]!=s[id-len[u]-1]) u=fail[u];
	return u;
}
void solve(){
	cin>>s; n=s.length();
	for(int i=0;i<=n;i++) dp[i]=INF;
    //注意 dp 值初始都设为极大
	s=" "+s;
	tot=1,last=0;
	len[1]=-1,fail[0]=1;
	int ans=n;
	dp[0]=1; //先把翻转的代价算上，不然像转移一那种就计算不到
	for(int i=1;i<=n;i++){
		int fa=getfail(last,i);
		if(!trie[fa][getid(s[i])]){
			fail[++tot]=trie[getfail(fail[fa],i)][getid(s[i])];
			trie[fa][getid(s[i])]=tot;
			len[tot]=len[fa]+2;
            //下面求 trans
			if(len[tot]<=2) trans[tot]=fail[tot];
			else if(len[tot]%2==0){
				int tmp=trans[fa];// 很重要 保证时间复杂度
                // 这样可以保证 Fail 边不会被大量重复走过
				while(s[i-1-len[tmp]]!=s[i]||(len[tmp]+2)*2>len[tot]) tmp=fail[tmp];
				trans[tot]=trie[tmp][getid(s[i])];
			}
			if(len[tot]%2==0){
				dp[tot]=min(dp[fa]+1,dp[trans[tot]]+len[tot]/2-len[trans[tot]]+1);
				ans=min(ans,dp[tot]+n-len[tot]);
			}
		}
		last=trie[fa][getid(s[i])];
	}
	cout<<ans<<"\n"; 
	for(int i=0;i<=tot;i++){
		for(int j=0;j<4;j++) trie[i][j]=0;
	}
}

参考文章

• PAM 题解 by 功在不舍

• oi-wiki

• 来自 zeb 的讲解