备战蓝桥杯，第八章：位运算符和操作符属性

一.操作符的分类

|---------|-------------------------------------------|
| 分类 | 操作符 |
| 算术操作符 | + - * % / |
| 移位操作符 | << >> |
| 位操作符 | & | ^ |
| 赋值操作符 | = += -= *= /= %= <<= >>= &= |= ^= |
| 单目操作符 | ! ++ -- & * + - ~ sizeof (类型) |
| 关系操作符 | > >= < <= == != |
| 逻辑操作符 | && || |
| 条件操作符 | ? : |
| 下标引用操作符 | [ ] |
| 函数调用操作符 | ( ) |

上述的操作符，以前章节有些许涉及，本章节继续介绍一组和位运算相关的操作符。这些操作符和二进制的知识有关系，下面先讲解二进制的相关知识。

二.二进制和进制转换

我们经常听到的二进制、八进制、十进制、十六进制是什么意思呢？

其实所有进制只是数值的不同表示形式而已。比如：数值15的各种进制的表示形式：

15的二进制：1111

15的八进制：17//八进制数值的前面写0

15的十进制：15

15的16进制：F//16进制的数值前面写0X

下面重点介绍一下二进制：十进制是我们日常生活中的最常用的进制。下面普及一下进制的基本常识：

• 十进制中满10进1
• 十进制的数字是由0~9的数字组成的
• 二进制是满2进1
• 二进制是由0和1数字组成的

（1）二进制转十进制

其实十进制的123表示的是一百二十三，为什么呢？

十进制的每一位数字都有自己对应的权重。十进制的数字从右向左是个位、十位、百位......，分别每一位的权重是1、10、100......如下图所示：

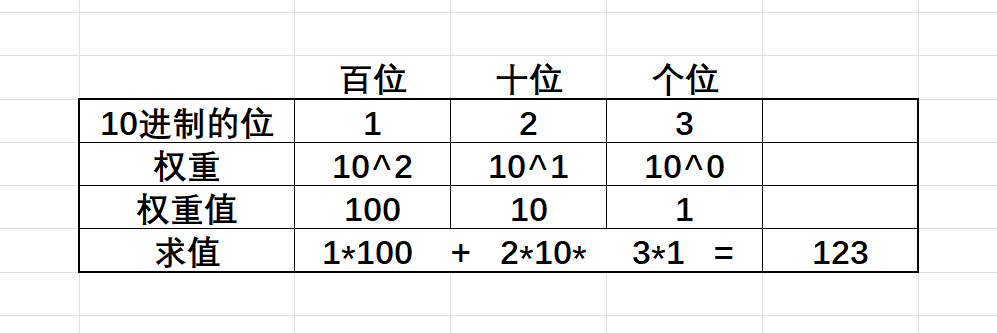
二进制和十进制是类似的，只不过二进制的每一位的权重，从右向左是：1、2、4、8......，下面是二进制的权重理解：

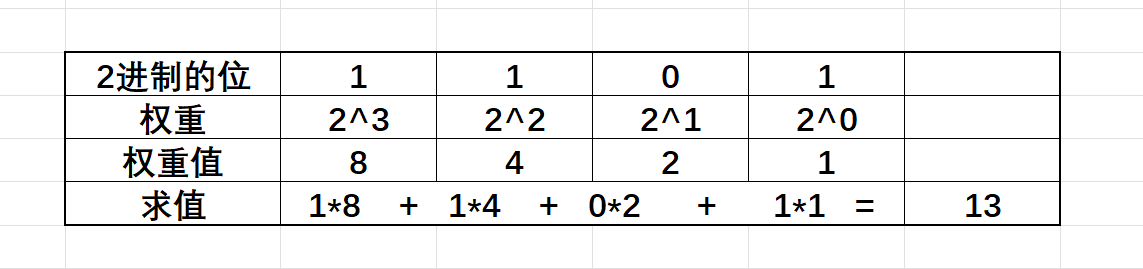
八进制转十进制数，方法类似，只是权重是从8开始，然后依次是：1、8、......16。16进制也是类似的道理。

（2）十进制转二进制

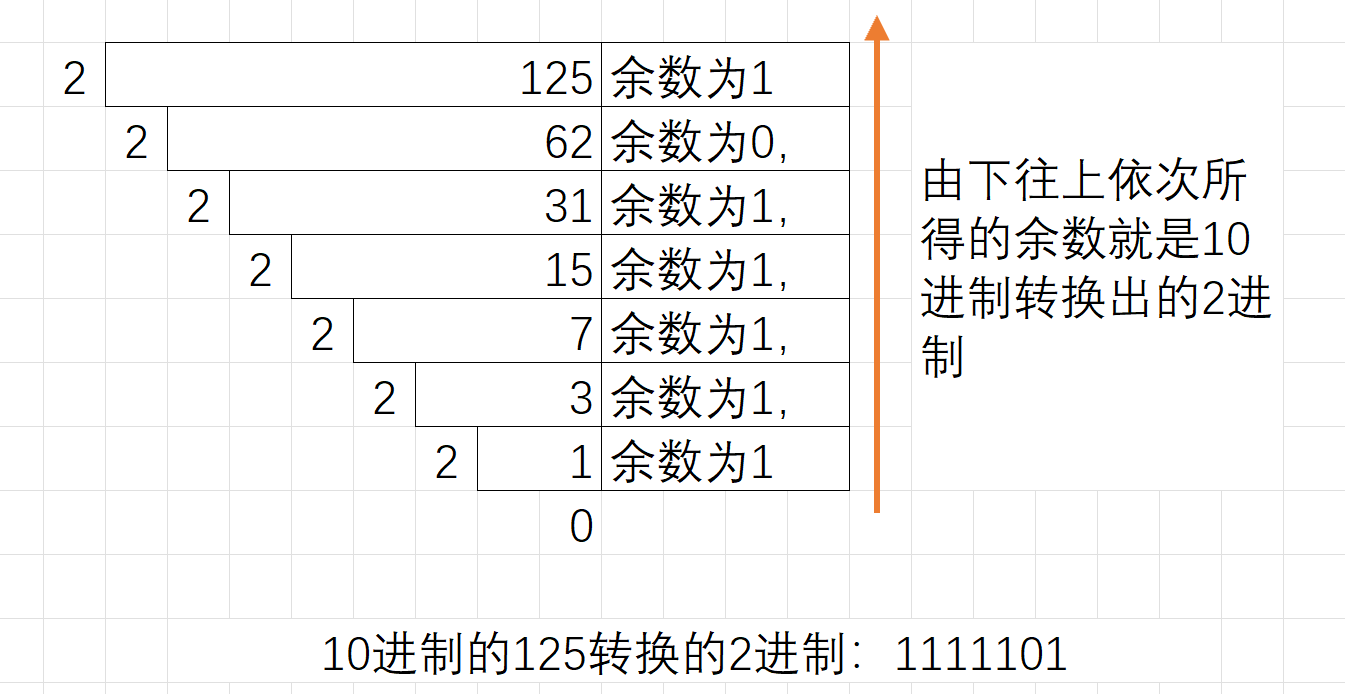
（3）二进制转八进制

八进制的数字每一位是0~7的数字，0~7的数字中，各自写成二进制，最多有3个二进制位组成，比如7的二进制是111，所以在二进制转8进制的时候，从二进制序列中右边低位开始向左每3个二进制位换算一个八进制位，剩余不够3个二进制位的直接换算。如二进制的01101011，换算成8进制为0153。（0开头的数字，编译器会被认为是八进制数字）

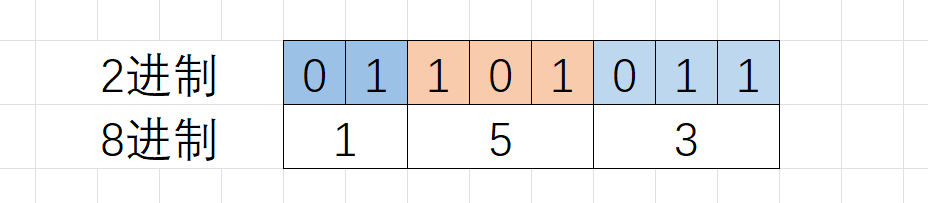
八进制数字转换为二进制数，需要将每一个八进制为转换为3个二进制位即可。

（4）二进制转十六进制

十六进制的数字每一位是0~9、a~f。每位各自写成二进制数字，最多有4个二进制位就足够了，比如f的二进制是1111，所以在二进制转十六进制时，从二进制序列中右边低位开始向左每4个二进制位会换算一个十六进制位，剩余不够4个二进制位的直接换算。如二进制的01101011换成十六进制为0X6b，十六进制表示应该在数字之前加上0X。

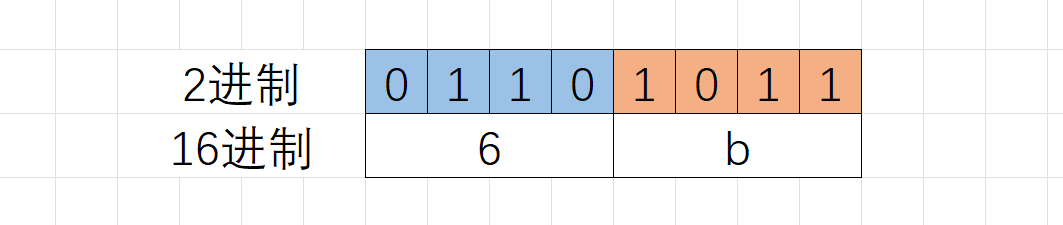
十六进制转换为二进制应该，每一位16进制位转换位3个二进制位就行。

（5）原码、反码、补码

二进制在计算机内部都是以二进制的补码形式存储的。下面讲解下二进制的表示形式：

移位运算符：>>

位运算符 ： & | ^

整数的二进制表示方法有三种，即原码、反码、补码；整数分为有符号整数和无符号整数。

有符号整数的原码、反码和补码的二进制表示均由符号位和数值位两部分组成，二进制序列中，最高位的那一位被当作符号位，剩余位都是数值为。符号位是0表示正，用1表示负。正整数的原码、反码、补码相同，负数的三种表示方法各不相同，需要计算：

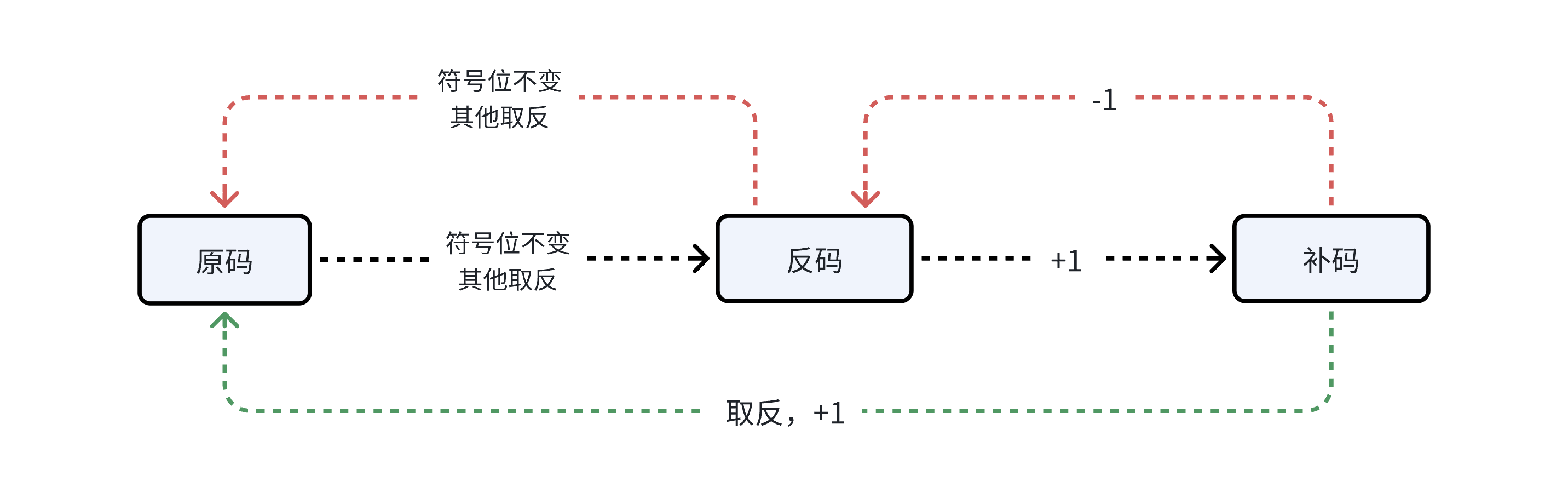
原码：直接将数值按照正负数的形式翻译成二进制得到的就是原码。

反码：将原码的符号位不变，其余位依次按位取反就可以得到反码。

补码：反码+1就得到了补码。

int a = -10;
//原码：10000000 00000000 00000000 00001010
//反码：11111111 11111111 11111111 11110101
//补码：11111111 11111111 11111111 11110110
int a = 10;
//原码：10000000 00000000 00000000 00001010
//反码：10000000 00000000 00000000 00001010
//补码：10000000 00000000 00000000 00001010

无符号整数的三种二进制表示相同，没有符号位，每一位都是数值位

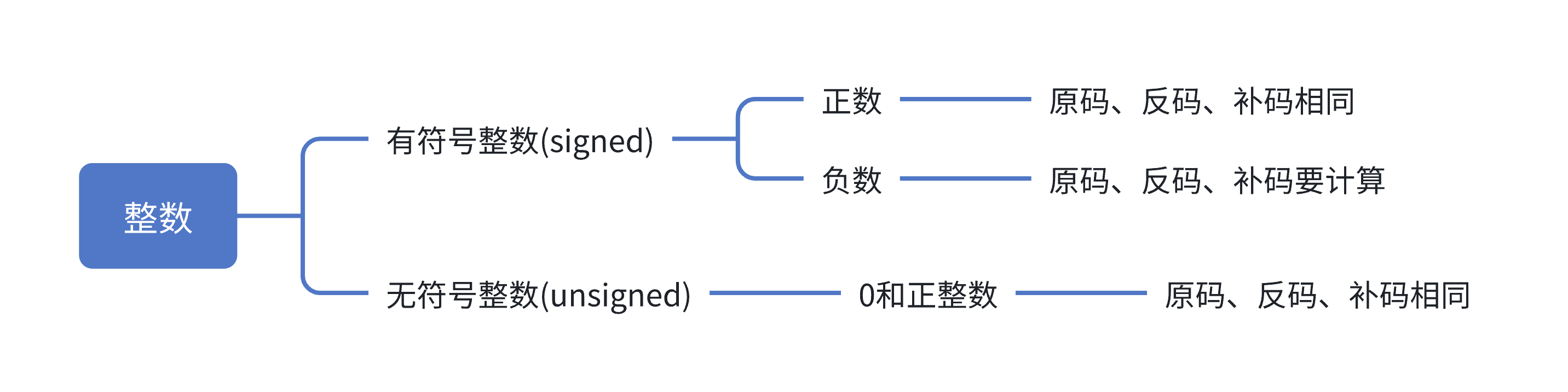
整数在内存中以补码的形式存储，整数在参与位运算时，是使用内存中的补码进行计算的，计算的结果也是补码，需要转换成原码才是真实显示出来的真实值。

为什么整型在内存中存放的是补码呢？

在计算机系统中，整数的数值一律用补码来表示和存储。原因在于使用补码计算时，可以将符号位和数值位统一进行处理。此外补码与原码相互转换，其运算过程是相同的，不需要额外的硬件电路。

三.位运算操作符

<< //左移操作符

>> //右移操作符

& //按位与操作符

| //按位或操作符

^ //按位异或操作符

~ //按位取反操作符

上面的运算符只适合于整数的计算，不能应用于其他数据类型的计算。

（1）左移位操作符

左移位操作符是双目操作符，形式如下：

int num = 10;
num << i; //将num的⼆进制表⽰，左移i位 

代码演示：

#include <iostream>
using namespace std;
int main()
{
 int num = 10;
 int n = num << 1;
 cout << "n = " << n << endl;
 cout << "num = " << num << endl;
 return 0;
}

左移位操作符的移位规则：左边丢弃，右边补0。下面是运算过程：

（2）右移位操作符

右移位操作符也是双目操作符，运算形式如下：

num >> i;//将num的⼆进制表⽰右移i位 

代码演示：

#include <iostream>
using namespace std;
int main()
{
 int num = -1;
 int n = num >> 1;
 cout << "n = " << n << endl;
 cout << "num = " << num << endl;
 return 0;
}

右移位操作符分为两种运算形式：逻辑右移和算数右移，具体那种右移方式取决于编译器，大部分的编译器采用的是算数右移。两种移位操作如下：

• 逻辑右移：左边用0填充，右边丢弃。
• 算术右移：左边用符号位数字填充，右边丢弃。

下面是相关的运算操作：

逻辑右移：

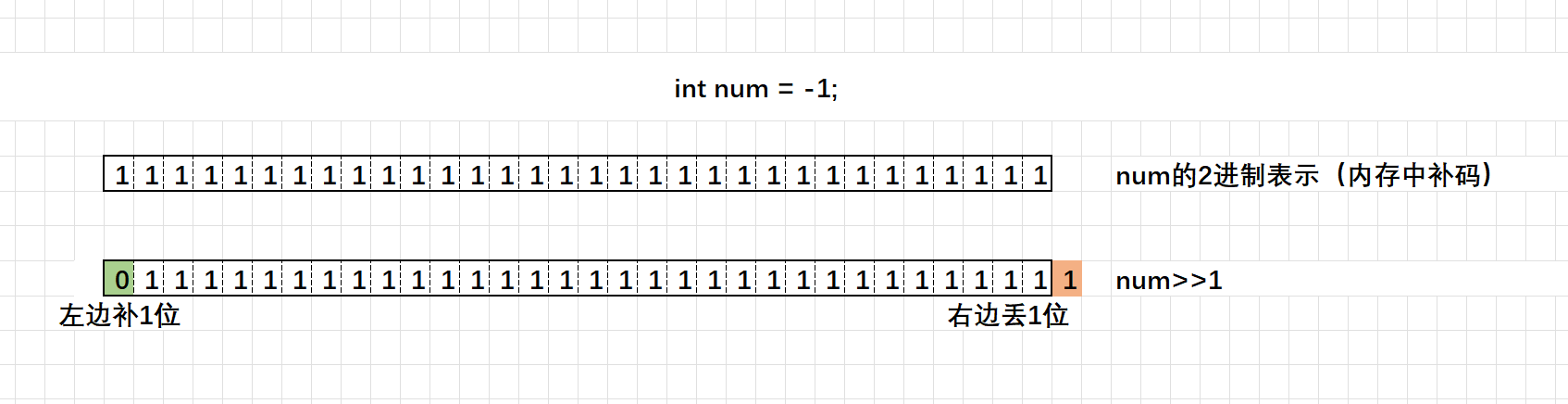
算数右移：

对于移位操作符来说，操作数不能是负数，这种行为是未定义的行为。编译器会报错的。下面是必须避免的错误示范：

int num = 10;
num >> -1;//error

（3）按位与操作符

按位与操作符是双目操作符，形式如下：

a & b; //a和b按位与运算 

规则：对于两个数的二进制位进行与运算，只有对应的两个二进制位都为1时，结果才为1。计算详情如下：

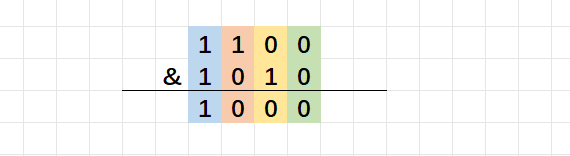
代码演示：

#include <iostream>
using namespace std;
int main()
{
 int a = -5;
 int b = 7;
 int c = a & b;
 cout << c << endl;
 return 0;
}

解析：

-5的原码：10000000 00000000 00000000 00000101

-5的反码：11111111 11111111 11111111 11111010

-5的补码： 11111111 11111111 11111111 11111011

7的补码：00000000 00000000 00000000 00000111

两数的按位与运算过程如下：

计算得到的二进制数字是： 00000000 00000000 00000000 00000011，这个二进制序列当作补码时，最高位是1，说明是正数，所以原码、反码、补码相同，最终化为十进制数位3。

（4）按位或操作符

按位或操作符是双目操作符，形式如下：

a | b; //a和b按位或运算 

规则：对于两个数的对应二进制位进行或运算，对应的两个二进制只要有1，按位或的结果就为1。

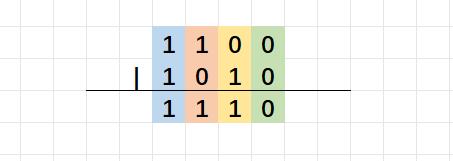
代码演示：

#include <iostream>
using namespace std;
int main()
{
 int a = -5;
 int b = 7;
 int c = a | b;
 cout << c << endl;
 return 0;
}

解析：

-5的原码：10000000 00000000 00000000 00000101

-5的反码：11111111 11111111 11111111 11111010

-5的补码：11111111 11111111 11111111 11111011

7的补码：00000000 00000000 00000000 00000111

两者按位或的计算过程如下：

计算得到的二进制序列是11111111 11111111 11111111 11111111，这个二进制序列当作补码时，且最高位是1，说明是负数，计算的原码是：10000000 00000000 00000000 00000001，所以最终十进制的结果为-1。

（5）按位异或操作符

按位异或操作符i是双目操作符，形式如下：

a ^ b; //a和b按位异或运算 

规则：对两个数的对应二进制进行异或运算，对应的两个二进制相同则为0，相异则为1。下面是相关计算过程：

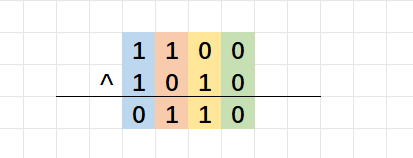
代码演示：

#include <iostream>
using namespace std;
int main()
{
 int a = -5;
 int b = 7;
 int c = a ^ b;
 cout << c << endl;
 return 0;
}

解析：

-5的原码：10000000 00000000 00000000 00000101

-5的反码：11111111 11111111 11111111 11111010

-5的补码：11111111 11111111 11111111 11111011

7的补码：00000000 00000000 00000000 00000111

-5的补码和7的补码按位异或运算如下：

计算得到的二进制序列是：11111111 11111111 11111111 11111100，这个二进制序列当作补码时，且最高位是1，说明是负数，求的原码是：10000000 00000000 00000000 00000100，所以最终计算的二进制是-4。

（6）按位取反操作符

按位取反操作符是单目操作符，形式如下：

~a; //对a的⼆进制位按位取反 

规则：对操作数的二进制位进行按位取反运算，二进制数字是0变成1，1变成0。

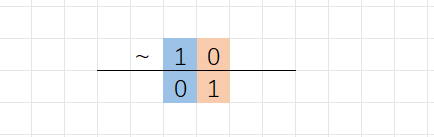
代码演示：

#include <iostream>
using namespace std;
int main()
{
 int a = -5;
 int b = ~a;
 cout << b << endl;
 return 0;
}

解析：

-5的原码：10000000 00000000 00000000 00000101

-5的反码：11111111 11111111 11111111 11111010

-5的补码：11111111 11111111 11111111 11111011

对-5的补码按位取反运算过程如下：

计算得到的二进制序列是：00000000 00000000 00000000 00000100，这个二进制序列当作补码时，且最高位是0，说明是正数，所以原码与补码相同，最终化成十进制的结果是-4。

四.位运算符的应用

（1）判断奇偶数

所有偶数的二进制表示中，最低位一定是0，所有奇数的二进制表示中，最低位一定是1。所以将一个数字与1进行按位与运算，即可判断这个数是奇数还是偶数。

(x&1) == 1 说明x是奇数

(x&1) == 0 说明x是偶数

代码演示：

#include <iostream>
using namespace std;
int main()
{
 int n = 0;
 cin >> n;
 if ((n & 1) == 1)
 cout << "odd" << endl;
 else
 cout << "even" << endl;
 return 0;
}

（2）保留二进制的指定位

有时候需要从一个整数x的二进制中取出某个位或某几个位，使取出的位置上保留原来的值，其他位置为0，这时候可以使用一个值m，使m的二进制位中对应的位置为1，其他位为0。然后使这两个数按位与即可。计算详情如下：

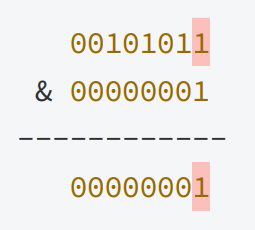
比如：取出x的最低四位，则只需要将x与末尾四位是1，其余为0，进行按位与运算。计算过程如下：

再比如：取出x的最低2~4位，则只需要将x与最低2~4是1，其余位是0的数进行按位与计算。计算过程让如下：

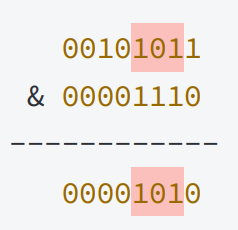
假设我们有一个权限标志位，存储在一个变量中，我们可以通过按位与操作来检查某个特定位是否被设置。

（3）获取二进制的指定位

我们需要获取一个整数x的二进制序列的第i位（从低到高，以最低位为第0位）的具体数字时，可以对x进行下面的运算：

class Solution {
public:
 uint32_t reverseBits(uint32_t n) {
 int i = 0;
 uint32_t ret = 0;
 for (i = 0; i < 32; i++)
 {
 int b = (n >> i) & 1; //从低往⾼获取每⼀个⼆进制位 
 b <<= (31 - i); //从低位移动到⾼位 
 ret |= b; //将这⼀位设置到ret中 
 }
 return ret;
 }
};

如果结果是0，表示第i位是0；如果结果是1，表示第i位是1。比如：确定x的二进制序列的第三位的值，需要将x右移3位，第三位就是最低位，然后和1进行按位与计算即可。

x: 00101011 右移三位后：

00000101

& 00000001

---

00000001

（4）将指定二进制位设置为1

有时候需要将一个整数x的二进制表示中的某一位设置为1，其余位保留原值。就可以使用另外一个数m，使m的二进制上对应的位置为1，其余位置为0。然后使两个数进行按位或运算，就可以得到想要的值。比如：将x的后四位二进制序列设置为1，其余位保持不变，只需要将x与后四位为1，其余位为0的数字进行按位或运算。

x: 00101011

| 00001111

---

00101111

当然也可以只设置x二进制序列的某一位为1，也就是将x二进制的第i位置为1，就只需要进行下面的运算：

将x=00101011的第四位二进制序列置为1，其余位保持原有的值不变。只需要将x与00010000进行按位或运算：

x: 00101011

| 00010000 //这个数字可以通过 1得到

---

00111011

（5）将指定的二进制位设置为0

有时候需要将一个整数的二进制序列中某一位设置为0，其余位保留原值。也就是将x的二进制的第i位置为0，其余值保持不变。下面举出相关例子进行计算：

将x=00001011的第三位置为0，其余位保持不变。则只需要将x=00001011与m=11110111进行按位与运算。下面是运算过程：

x: 00001011

& 11110111 //这个数字可以通过 1，后然后按位取反得到

---

00000011

（6）反转指定的二进制位

有时候需要将一个整数的二进制表示中的第i位反转，也就是从原来的1变为0，从原来的0变为1。这种操作只需要将使用另一个数m，m的二进制序列中第i位为1，其余位为0.然后让两个数进行按位异或运算，就可以得到想要的数。比如：

将x=00101011的第二位反转，只需要将x=00101011与m=00000100进行按位异或运算，计算过程如下：

00101011

^ 00000100

---

00101111

（7）将二进制中最右边的1变为0

有时候需要将一个整数的二进制表示中最右边的1变成0，这时候就可以使用这个数字的二进制表示x与x-1进行合取运算，比如：

将x=00101100二进制中最右边的1变为0，只需要x=00101100&(x-1)=00101100即可，下面是详细的计算过程：

00101100 (x)

& 00101011 (x-1)

---

00101000

这种运算通常应用到求一个数的二进制序列中有几个1，因为x=x&(x-1)这种运算，每计算一次就会将x的二进制序列的最右边的1置为0。那么只要循环不断执行该操作，直到该数的二进制序列变为全0即可。此时的循环次数就是该数的二进制序列的1的个数。

（8）只保留二进制最右边的1

有时候需要将一个整数的二进制序列表示的最右边的1保留下来，其余位置为0，那么只需要将x&(-x)即可。比如：

将x=00101100的最右边的1保留，其余位置的数字置为0，就只需要将其与-x=00101100进行合取得到的结果就是想要的结果。下面是详细的计算过程：

x的⼆进制：00101100

-x的原码 ：10101100

-x的反码 ：11010011

-x的补码 ：11010100

00101100（x）

& 11010100（-x）

---

00000100

这种运算的性质可以帮助我们判断一个数是否是2的幂数？下面是相关代码演示：

bool isPowerOfTwo(int n) 
{
 return (n > 0) && (n & -n) == n;
}

因为2的幂次方的数字的二进制序列中只有一个1，n&-n会将这个1保留下来，其实还是n，所以只要完成上述变化后值没有改变的数就是2的幂次方数。

（9）异或的运用

下面是整理的异或运算的特点：

1. x ^ x = 0 两个相同数字异或的结果
2. 0 ^ x = x 0和任何数异或的结果等于任何数本身
3. a ^ b ^ a = a ^ a ^ b 异或操作符支持交换律

下面是异或运算符的运用示例：

练习：交换两个整数的值

#include <iostream>
using namespace std;
int main()
{
 int a = 0;
 int b = 0;
 cin >> a >> b; 
 cout << "交换前：a = " << a << " b = " << b << endl;
 a = a ^ b; //a' = a ^ b
 b = a ^ b; //b' = a' ^ b == a ^ b ^ b == a
 a = a ^ b; //a = a' ^ b' == a ^ b ^ a == b
 cout << "交换后：a = " << a << " b = " << b << endl;
 return 0;
}

上述代码利用异或运算符的第三条性质，将两个整数的位置进行交换。使用异或交换两个数的值，只能适用于整型类型的数，因为异或运算仅适用于整型类型。

五.操作符的属性

1.优先级

优先级指的是：如果一个表达式包含多个运算符，哪个运算符应该优先执行。各种运算符的优先级是不一样的。比如：我们小学就学过的先乘除后加减。

3 + 4 * 5;

上面的例子中，表达式中有加法和乘法。由于乘法运算符的优先级高于加法运算符的优先级，所以会先计算4*5，而不是先计算3+4。

2.结合性

如果两个运算符的优先级相同，优先级没办法确定先计算哪个，这时候就由结合性决定了。大部分运算符是左结合（从左向右执行），少数运算符遵循右结合（从右向左执行）

5 * 6 / 2;

上面示例中，乘法操作符和除法操作符的优先级相同，且都是左结合运算符，所以都是从左到右执行，先计算5*6，后计算6/2。下面是结合性优先级的相关表格：

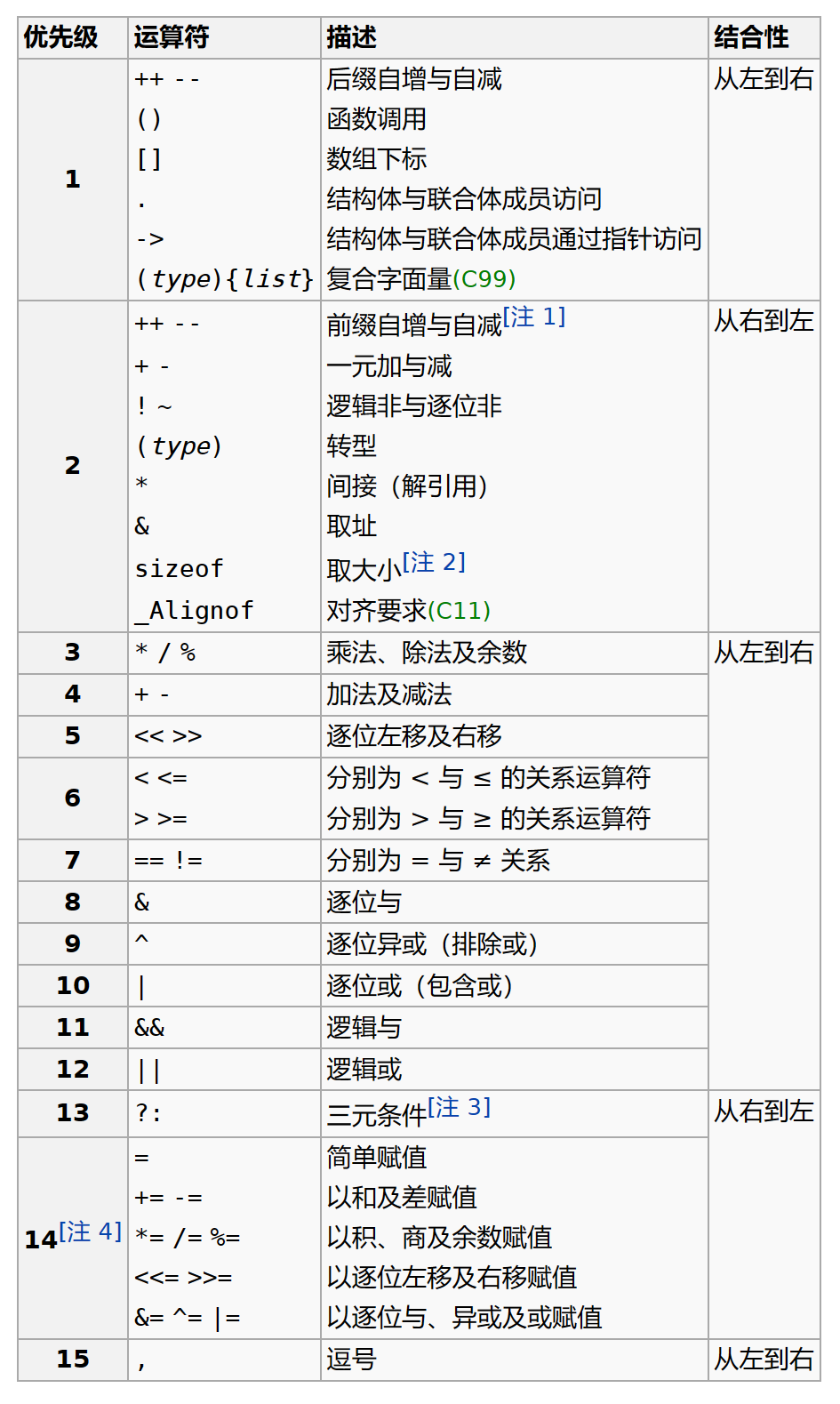
3.总结

当有了操作符的优先级和结合性，我们就可以确定一个表达式计算的顺序，但是如果一个表达式写的过于复杂，即使有了操作符的优先性和结合性，也可能无法确定表达式唯一的计算路径。所以在今后写代码时，应该避免写过于复杂的表达式。