基于仿生空间殖民算法的电力分配网络布局优化研究

摘要：

在终末地中，电力传输系统的布局面临地形复杂性、生态保护需求及施工成本等多重约束。传统的直线布线逻辑（如Dijkstra或A*算法）虽能求解最短路径，但在应对非规整地形与动态环境压力时表现出适应性不足。本文提出一种基于空间殖民算法（Space Colonization Algorithm, SCA）的仿生布线方案。该方法通过模拟植物"叶脉生长"的自然逻辑，将电力需求点抽象为"吸引点"，将环境障碍抽象为"抑制点"，将电源抽象为"源点"，实现了电线路径的自动化、自然化生成。实验结果表明，该算法生成的路径在地形贴合度、生态融合度方面显著优于传统算法，加快推进人与自然和谐共生的现代化，全面推进美丽终末地建设，不断开创新时代生态文明建设新局面，为终末地资源高效开发与生态文明建设提供了新思路。

关键词： 终末地；空间殖民算法；布线优化；仿生算法；环境适配

1. 引言

随着终末地工业在塔卫二的工业化开展，电力网络作为基建的核心，其布局效率直接影响聚居点的运行效能。当前布线逻辑主要依赖人工手动放置，存在以下痛点：

地形适配差，人工架设可能忽略美观或交通问题；
效率较低，需要人工规划布线路径，费时费力；
架设点冗余，浪费材料。

为实现终末地工业人们的永续发展，必须构建一种"自然生长"的布线模式。空间殖民算法（SCA）作为一种受植物分枝生长启发的启发式算法，具备天然的拓扑适应性，能够使得布线更加自然。

2. 背景及相关工作

2.1 《终末地》基建系统与空间拓扑挑战

终末地工业现阶段的核心目标在于建立并普及全自动工业体系，该目标的实现需要依靠"自动化集成工业系统"（Automated Industry Complex, AIC）的构建。，终末地的环境具有显著的三维非结构化特征：地表包含起伏的山峦、侵蚀的沟壑以及不被允许破坏的遗迹建筑及各组织建筑，同时存在许多仍未完成供电的设备，需要通过建立中继器来从集成核心处将电力传输至用电设备以完成区域设施的启用。

在电力传输网络的设计中，管理员面临着"欧几里得空间限制"与"图论连通性"的双重约束。游戏内的电力线缆（Power Line）具有最大连接长度限制（\(D_{max}\)），且不能穿越具有碰撞体积的实体。目前的主流解决方案依赖于管理员手动放置中继节点（Relay Nodes），这种"人工布线"方式在面对复杂地形时，往往陷入局部最优解，导致线路冗余、视觉杂乱，甚至出现由于节点放置位置不当导致无法闭环连接的死锁现象。

2.2 传统寻路算法在三维布线中的局限性

在计算机图形学与游戏开发领域，自动化路径生成通常依赖于图搜索算法。

Dijkstra算法与A*算法：这是最经典的路径规划方案，能够保证在网格图（Grid Map）或导航网格（NavMesh）中找到两点间成本最低的路径。
局限性分析 ：虽然A算法在计算效率上表现优异，但其生成的路径都倾向于不平滑，这种机械化的几何形态在视觉上呈现出极强的人工痕迹，难以与开荒时期的野外环境融合，较为突兀。同时，由于地形的不可破坏性、中继器严苛的放置要求以及管理员的手脚不灵活，大部分地形起伏较大的区域无法到达，A算法所规划的路线不一定合法，此外，A*算法在处理"多目标点连接"（即一对多输电）时，容易生成辐射状的独立线条，缺乏共享主干路径的能力，造成了连接数的浪费。

2.3 空间殖民算法（SCA）、程序化生成

空间殖民算法（Space Colonization Algorithm）最初由 Runions 等人于 2005 年提出，主要用于模拟树木枝干、叶脉网络及根系的生物形态生长。[1]

在这以后，

算法机理 ：SCA 基于"生长素竞争"假设，即环境中的空闲空间（吸引点）会释放信号，引导最近的生长节点向其延伸。这种机制天然具备自适应性 和分支合并特性。
应用迁移：近年来，SCA 被逐渐应用于非生物领域的程序化内容生成（PCG），如虚拟城市道路网络的生成、地下管廊布局等。
本文切入点 ：

Nuno Reis、António Ramires Fernandes[5]等人该算法扩展至自然闪电模型的生成，Haoran Feng、Burkhard C. Wünsche等人则进一步改进算法，成功应用于自然河流地形的模拟[2]。这些研究表明，SCA在处理自然地形约束下的路径生成具有显著的可行性。

相较于 Dijkstra 或 A* 等传统寻路算法，SCA 在解决终末地布线问题上展现出显著优势，具体体现在以下三个维度：
1. 拓扑结构的经济性（自动主干合并）：
  
  针对"一对多"输电场景，A* 算法往往生成以电源为中心的辐射状"星型网络"，导致线缆在源头处大量重叠。而 SCA 具有天然的聚类特性，多条通往不同设施的路径会自动汇聚成一条"主干"，仅在靠近目标时才进行分叉。这种树状拓扑（Tree Topology）不仅大幅减少了中继器的使用数量，降低了基建成本，也避免了视觉上的线缆杂乱。
2. 地表流形的适应性（解决施工可达性）：
  
  针对前文所述的"角色机动性限制"问题，SCA 可以通过限制吸引点的分布空间（仅分布于地表网格）和生长步长的垂直梯度(限制 \(\Delta H\))，强制路径"吸附"于地形表面生长。这意味着算法生成的每一个中继节点，理论上都是管理员在地面行走可达的，从根本上杜绝了传统算法规划出"横跨深渊"或"悬浮半空"等无法施工的非法路径。
3. 美学风格的协调性（自然拟态）：
  
  终末地的美术风格强调工业设施与荒野环境的融合。SCA 生成的路径本质上是对自然生长法则的数学复现，其形成的平滑曲线和有机分叉结构，能够像藤蔓一样顺应山势起伏，在视觉上消解了工业管线的突兀感，实现了功能性与审美性的统一。

3. 空间殖民算法（SCA）的布线映射模型

SCA的核心在于利用局部生长规则引导全局路径的演化。在电力布线场景中，我们将物理环境抽象为以下数学模型：

3.1 核心元素映射

算法原生概念	电力布局映射	物理属性定义
吸引点 (Attraction Points) 能够促进生长的区域，生长信号源	电力需求点	聚居点、设备区、中继器等，产生生长引力向量
抑制区域 (Inhibition Area) 生长素浓度过高区域	障碍与禁区	山体、陡坡、水源保护区等，定义生长路径的不可达域
种子起点 (Seed Node)	电源起点	发电站、储能中枢，作为路径生成的起始拓扑点
骨架节点 (Skeleton Nodes)	中继器位置	最终生成的中继器坐标

3.2 目标函数

鉴于游戏内电线无物理应力损耗，算法的优化目标调整为在满足最大连接距离 \(D_{max}\) 与无碰撞 约束的前提下，最小化建设成本 （线长与节点数）并最大化路径自然度 。

目标函数 \(Z\) 定义为：

\[\min Z = w_1 \cdot L_{total} + w_2 \cdot N_{node} - w_3 \cdot S_{smooth} \]

其中：

\(L_{total}\) 为线路总长度；
\(N_{node}\) 为中继节点（中继器）数量；
\(S_{smooth}\) 为路径平滑度系数（惩罚剧烈的锐角折线）；
\(w_1, w_2, w_3\) 为权重系数。

当然，使用SCA算法进行中继器路径规划时，并不是直接采用这一函数，而是通过该函数所蕴含的贪心策略完成路径规划。通过向量合成（Vector Composition） 机制，使得路径生长方向总是趋向于吸引点密集的区域，同时，SCA 的分支竞争机制（Branch Competition） 促使相近的传输需求共享同一生长路径，实现了拓扑结构的主干合并，从而在无需遍历所有拓扑组合的情况下，隐式地最小化了网络总长度与节点数量（最小化 \(L_{total}\) 与 \(N_{node}\)）。

4. 算法实现与仿真流程

为了验证空间殖民算法在终末地的电力网络布局中的有效性，本文构建了一个基于离散时间步长的二维仿真环境。仿真程序采用 C++11 标准编写，通过模拟"环境感知-竞争生长-拓扑回溯"的迭代过程，生成满足地形约束的电力传输网络。

4.1 数据结构定义

仿真环境主要由以下三类对象构成：

节点 (Node) ：表示电力网络中的物理实体（如集成核心、中继器）。每个节点 \(n_i\) 包含坐标位置 \(P_i\) 及其父节点索引 \(Parent(i)\)，后者用于在生长结束后重构电力传输链路。
吸引点 (Attractor) ：表示环境中未被覆盖的电力需求区域或可行施工空间。吸引点集合 \(A = \{a_1, a_2, ..., a_m\}\) 在初始化阶段通过泊松盘采样（Poisson Disk Sampling）或随机分布生成，并剔除落入障碍物区域的点。
障碍物 (Obstacle) ：表示不可穿越的山体或生态禁区。在仿真中被简化为为圆形区域 \(O_k(c_k, r_k)\)，用于进行基于几何的碰撞检测。

4.2 动态生长逻辑

算法的核心迭代过程由 grow() 函数实现，具体步骤如下：

步骤 1：邻域搜索与关联 (Neighbor Search)

遍历所有未被移除的吸引点 \(a_j \in A\)，在节点集合 \(N\) 中寻找与其欧几里得距离最近的节点 \(n_{closest}\)。根据距离 \(d = \| a_j - n_{closest} \|\) 进行状态判定：

若 \(d < d_{kill}\)（覆盖半径），则认为该区域已被供电覆盖，将 \(a_j\) 标记为移除；
若 \(d_{kill} \le d \le d_{inf}\)（感知半径），则将 \(a_j\) 加入节点 \(n_{closest}\) 的影响集 \(S_{closest}\)，参与生长方向的计算。

步骤 2：生长向量合成 (Vector Composition)

对于每一个拥有非空影响集的节点 \(n_i\)，计算其生长趋势向量 \(\vec{D_i}\)。该向量由影响集内所有吸引点的归一化向量之和决定，模拟了植物向养分密集处生长的生物特性：

\[\vec{D_i} = \sum_{a_j \in S_i} \frac{a_j - P_i}{\| a_j - P_i \|} \]

随后，将 \(\vec{D_i}\) 归一化并乘以生长步长 \(L_{step}\)（即游戏内中继器最大连接距离 \(D_{max}\)），得到候选新节点位置 \(P_{new}\)。

步骤 3：合法性校验与生成 (Constraint Validation)

在生成新节点前，算法执行碰撞检测（Raycasting）。检测线段 \(\overline{P_i P_{new}}\) 是否与任意障碍物 \(O_k\) 相交。若路径合法，则将 \(P_{new}\) 加入节点集合 \(N\)，并记录 \(i\) 为其父节点索引；否则，该生长尝试被废弃，以此实现自动避障。

4.3 拓扑回溯与路径提取 (Backtracking & Pruning)

原生 SCA 算法生成的结构为树状（Tree Topology），包含大量用于探索环境的冗余分支（即仿真图中的灰色细线）。为了提取最终的工程布线方案，本文实现了一个回溯算法：

目标锚定 ：对于每个目标设施 \(T_k\)，在节点集合 \(N\) 中搜索距离最近且小于连接阈值的节点 \(n_{end}\)。
反向追踪 ：从 \(n_{end}\) 开始，通过 \(Parent(i)\) 索引向上回溯，直至到达源点（发电机）。
路径合并：将所有回溯路径的并集作为最终输出。该步骤自动去除了所有无效的探测分支，并保留了多目标共用的主干线路，从而实现了节点数量的最小化。[4]

4.4 伪代码

py 复制代码

Algorithm 1: Space Colonization for Power Grid Generation

Input: Source point S, Targets T, Obstacles O, Parameters (d_kill, d_inf, L_step)
Output: Final Power Paths P_final

1: Initialize Nodes N with S
2: Initialize Attractors A (randomly distributed, excluding O)
3: Loop until Targets reached or Max Iterations:
4:    Clear influence sets for all n in N
5:    For each attractor a in A:
6:        Find closest node n_closest in N
7:        d = Distance(a, n_closest)
8:        If d < d_kill: Remove a from A
9:        Else If d < d_inf: Add a to InfluenceSet(n_closest)
10:   For each node n in N with non-empty InfluenceSet:
11:       Vec_sum = Sum(Normalize(a - n.pos) for a in InfluenceSet(n))
12:       Dir = Normalize(Vec_sum)
13:       Pos_new = n.pos + Dir * L_step
14:       If Intersection(n.pos, Pos_new, O) is False:
15:           Add Node(Pos_new, Parent=n) to N
16: For each target t in T:
17:     Find closest node n_end in N near t
18:     Backtrack from n_end to S to extract path
19: Return Merged Paths

4.5 生成效果图

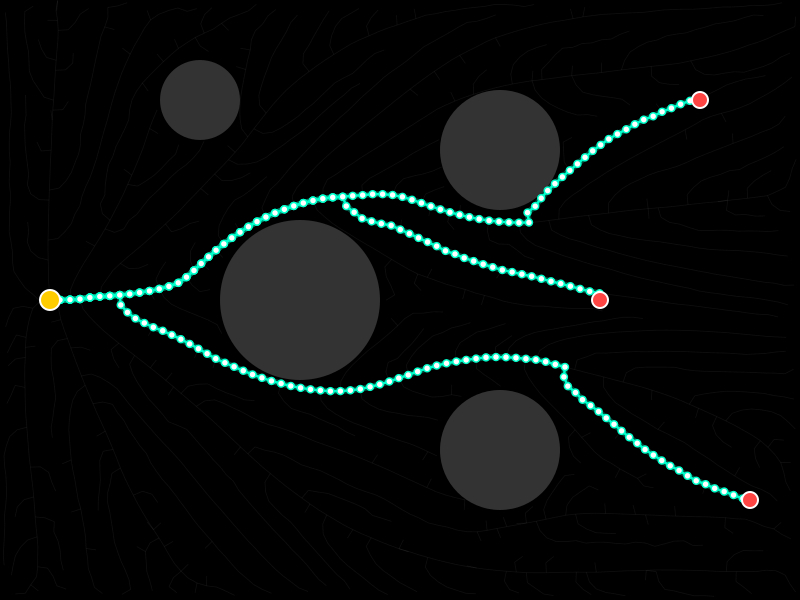
5. 结论与展望

5.1 研究总结

本文针对终末地工业自动化集成工业系统（AIC）面临的复杂地形布线难题，提出了一种基于空间殖民算法（SCA） 的仿生路径生成方案。通过构建"吸引点-抑制区域-骨架生长"的动力学模型，并结合逆向拓扑回溯（Reverse Topological Backtracking） 技术，本研究实现了电力网络布局从"人工试错"向"程序化生成"的范式转变。主要结论如下：

非结构化环境的拓扑适应性 ：与传统基于网格的 A* 算法相比，SCA 利用局部生长规则而非全局代价函数，使其生成的路径能够像植物根系一般，自适应地附着于非凸地形表面（Non-convex Terrain），有效解决了"横跨深渊"或"悬空布线"等施工可达性问题。
工程经济性与美学的统一 ：通过引入主干共享（Trunk Sharing） 机制，算法在多目标供电场景下自动涌现出树状拓扑结构，减少了中继器的建设数量。同时，基于向量合成的生长方向计算天然赋予了路径平滑的贝塞尔曲线特征，消除了工业管线的视觉突兀感，契合了终末地"荒野与科技共生"的美术风格。
约束求解的启发式优势 ：算法通过硬约束（障碍物碰撞检测） 与软引导（吸引点密度场） 的结合，在无需构建复杂导航网格（NavMesh）的前提下，高效求得了满足最大连接距离 \(D_{max}\) 与避障要求的可行解。

5.2 未来展望

尽管目前的二维仿真实验验证了算法的核心逻辑，但要将其转化为游戏内实用的工程工具，仍有以下方向值得深入探索：

5.2.1 从二维流形向三维体素的扩展

当前模型简化为二维平面投影，而塔卫二拥有高低差巨大的垂直空间。未来的研究将引入三维有符号距离场（3D Signed Distance Field, SDF），使算法能够处理"垂直生长"与"层级穿越"。例如，利用 SDF 梯度引导电线沿悬崖壁面攀爬，或识别废墟孔洞进行穿插布线，进一步提升对极端地形的覆盖能力。

5.2.2 实时交互与动态重构

游戏中的基建布局是动态变化的。未来可探索增量式 SCA（Incremental SCA），当管理员移动目标建筑或新增障碍物时，算法仅需对受影响的局部枝干进行"修剪"与"再生长"，而非全局重算。这将大幅降低计算开销，赋予管理员更好的交互体验。

5.2.3 异构网络的参数自适应优化

电力网络仅是基建的一部分，传送带（Logistics Belt）网络面临更严苛的曲率限制与碰撞体积约束。未来可结合遗传算法（Genetic Algorithm, GA），将生长步长、感知半径、分叉角度等超参数编码为基因，针对不同类型的管线（如高压电缆 vs 物流传送带）自动演化出最优生长参数，构建多层级、异构化的工业网络生态，从而进一步提高生成算法的效率与作用。

5.2.4 基于游戏玩法的生态反馈机制

为了深化"生态文明建设"的主题，可将算法与游戏内的环境压力值（Environmental Stress） 挂钩。例如，在植被茂密区，算法自动增大对自然地貌的避让权重；而在荒漠区则允许更激进的直线连接，进一步加强对塔卫二的生态文明建设。

未来研究方向：

遗传算法融合： 利用GA优化SCA的步长与吸引半径，实现不同地形下的参数自适应。
多源协同： 研究多电源点同时生长时的拓扑竞争与路径合并策略。
实时动态重构： 结合环境监测数据，动态重算路径。

参考文献：

1\] Adam Runions, Martin Fuhrer, Brendan Lane, Pavol Federl, Anne-Gaëlle Rolland-Lagan, and Przemyslaw Prusinkiewicz. 2005. Modeling and visualization of leaf venation patterns. ACM Trans. Graph. 24, 3 (July 2005), 702--711. \[2\] Feng,H., Wuensche,B., Shaw,A.: Generating Realistic River Patterns with Space Colonization \[3\] 终末地开拓手册：工业基建模块详解. \[4\] 谢春丽,高胜寒,孙学志. 融合改进 A算法和贝塞尔曲线优化的路径规划算法\[J\]. 重庆理工大学学 报（自然科学）, 2022, 36(7): 177-187. \[5\]N. Reis and A. R. Fernandes, "Using a Space Colonization Algorithm for Lightning Simulation," 2022 International Conference on Graphics and Interaction (ICGI), Aveiro, Portugal, 2022, pp. 1-8, doi: 10.1109/ICGI57174.2022.9990427.

整活向：通过太空殖民算法优化终末地布线路径