注:本文为 "复数概念与运算" 相关合辑。
略作重排,如有内容异常,请看原文。
复数概念及其四则运算
一、复数的基本概念
1. 虚数单位 i i i
定义 :规定虚数单位 i = − 1 i = \sqrt{-1} i=−1 ,其基本性质为 i 2 = − 1 i^2 = -1 i2=−1。
由定义可以得到 i i i 具有下面的性质:
i 1 = i , i 2 = − 1 , i 3 = − i , i 4 = 1 i^1 = i,\quad i^2 = -1,\quad i^3 = -i,\quad i^4 = 1 i1=i,i2=−1,i3=−i,i4=1
周期性 :虚数单位 i i i 的幂次运算具有周期性,周期为 4。对任意整数 n ∈ Z n \in \mathbb{Z} n∈Z,有
i 4 n = 1 , i 4 n + 1 = i , i 4 n + 2 = − 1 , i 4 n + 3 = − i i^{4n} = 1,\quad i^{4n+1} = i,\quad i^{4n+2} = -1,\quad i^{4n+3} = -i i4n=1,i4n+1=i,i4n+2=−1,i4n+3=−i
常用恒等式:
( 1 + i ) 2 = 2 i , ( 1 − i ) 2 = − 2 i , 1 + i 1 − i = i , 1 − i 1 + i = − i (1+i)^2 = 2i, \quad (1-i)^2 = -2i, \quad \frac{1+i}{1-i} = i, \quad \frac{1-i}{1+i} = -i (1+i)2=2i,(1−i)2=−2i,1−i1+i=i,1+i1−i=−i
2. 复数的定义与表示
代数形式 :设 x , y ∈ R x, y \in \mathbb{R} x,y∈R,称形如
z = x + y i z = x + yi z=x+yi
的数为复数 。其中 x x x 称为复数 z z z 的实部 ,记为 Re z = x \operatorname{Re} z = x Rez=x; y y y 称为复数 z z z 的虚部 ,记为 Im z = y \operatorname{Im} z = y Imz=y。
几何表示:
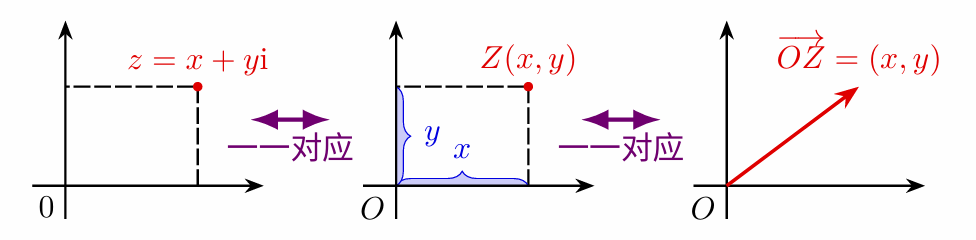
- 复平面内的点 Z ( x , y ) Z(x, y) Z(x,y)
- 平面向量 O Z → \overrightarrow{OZ} OZ ( O O O 为坐标原点)
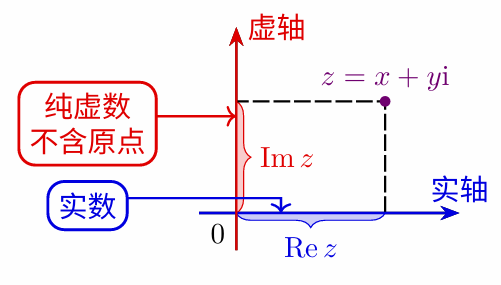
复平面中, x x x 轴称为实轴 , y y y 轴称为虚轴。
3. 复数的分类体系
复数 z = x + y i z = x + yi z=x+yi( x , y ∈ R x, y \in \mathbb{R} x,y∈R)的完整分类如下:
z = x + y i { 实数 ( y = 0 ) 虚数 ( y ≠ 0 ) { 纯虚数 ( x = 0 , y ≠ 0 ) 非纯虚数 ( x ≠ 0 , y ≠ 0 ) z = x + yi \begin{cases} \text{实数 } (y = 0) \\[6pt] \text{虚数 } (y \neq 0) \begin{cases} \text{纯虚数 } (x = 0, y \neq 0) \\[4pt] \text{非纯虚数 } (x \neq 0, y \neq 0) \end{cases} \end{cases} z=x+yi⎩ ⎨ ⎧实数 (y=0)虚数 (y=0){纯虚数 (x=0,y=0)非纯虚数 (x=0,y=0)
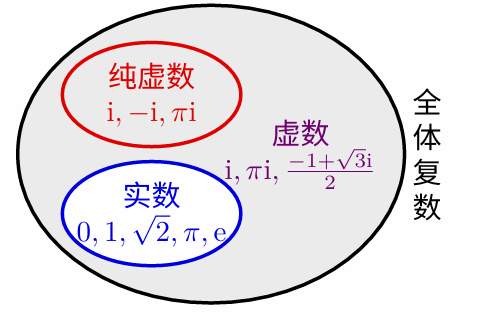
集合关系 :复数集 ⊃ \supset ⊃ 实数集,复数集 ⊃ \supset ⊃ 虚数集,虚数集 ⊃ \supset ⊃ 纯虚数集。
注意 :复数 y i yi yi( y ∈ R y \in \mathbb{R} y∈R)不一定是纯虚数,仅当 y ≠ 0 y \neq 0 y=0 时才是纯虚数。
复数集分类:
C { 实数 R { 有理数 Q { 整数 Z 分数 无理数 虚数 { 纯虚数 非纯虚数 \mathbb{C} \begin{cases} \text{实数 } \mathbb{R} \begin{cases} \text{有理数 } \mathbb{Q} \begin{cases} \text{整数 } \mathbb{Z} \\ \text{分数} \end{cases} \\[6pt] \text{无理数} \end{cases} \\[12pt] \text{虚数} \begin{cases} \text{纯虚数} \\[4pt] \text{非纯虚数} \end{cases} \end{cases} C⎩ ⎨ ⎧实数 R⎩ ⎨ ⎧有理数 Q{整数 Z分数无理数虚数{纯虚数非纯虚数
说明:
- 实数集 R \mathbb{R} R 与虚数集互不相交,且均为复数集 C \mathbb{C} C 的真子集;
- 有理数集 Q \mathbb{Q} Q 对四则运算封闭,整数集 Z \mathbb{Z} Z 为其真子集;
- 纯虚数集为虚数集的真子集,其元素实部为零且虚部非零。
复数集包含实数集与虚数集,虚数集包含纯虚数集;实数集可进一步划分为有理数集与无理数集,有理数集又可划分为整数集与分数集,由此构建起完整的数系分类体系。
4. 共轭复数
定义 :复数 z = x + y i z = x + yi z=x+yi 的共轭复数 定义为 z ˉ = x − y i \bar{z} = x - yi zˉ=x−yi。
性质:
| 性质 | 公式 |
|---|---|
| 共轭的共轭 | z ˉ ‾ = z \overline{\bar{z}} = z zˉ=z |
| 加减法 | z 1 ± z 2 ‾ = z ˉ 1 ± z ˉ 2 \overline{z_1 \pm z_2} = \bar{z}_1 \pm \bar{z}_2 z1±z2=zˉ1±zˉ2 |
| 乘法 | z 1 ⋅ z 2 ‾ = z ˉ 1 ⋅ z ˉ 2 \overline{z_1 \cdot z_2} = \bar{z}_1 \cdot \bar{z}_2 z1⋅z2=zˉ1⋅zˉ2 |
| 除法 | ( z 1 z 2 ) ‾ = z ˉ 1 z ˉ 2 \overline{\left(\dfrac{z_1}{z_2}\right)} = \dfrac{\bar{z}_1}{\bar{z}_2} (z2z1)=zˉ2zˉ1( z 2 ≠ 0 z_2 \neq 0 z2=0) |
| 模的关系 | z ⋅ z ˉ = ∣ z ∣ 2 = ∣ z ˉ ∣ 2 z \cdot \bar{z} = |z|^2 = |\bar{z}|^2 z⋅zˉ=∣z∣2=∣zˉ∣2 |
几何意义 :共轭复数在复平面内对应的点关于实轴( x x x 轴)对称。
二、复数的基本性质
1. 复数不能比较大小
定理:两个虚部不全为零的复数不能比较大小。
证明 (反证法):假设虚数单位 i i i 可与实数 0 0 0 比较大小。
- 若 i > 0 i > 0 i>0,两边同乘 i i i 得 i 2 > 0 i^2 > 0 i2>0,即 − 1 > 0 -1 > 0 −1>0,矛盾;
- 若 i < 0 i < 0 i<0,两边同乘 i i i 得 i 2 > 0 i^2 > 0 i2>0(不等号方向改变),即 − 1 > 0 -1 > 0 −1>0,矛盾。
故虚数之间不能比较大小,只有实数(虚部为 0 0 0)才能比较大小。
2. 复数相等的充要条件
定理 :设 z 1 = x 1 + y 1 i z_1 = x_1 + y_1 i z1=x1+y1i, z 2 = x 2 + y 2 i z_2 = x_2 + y_2 i z2=x2+y2i( x 1 , y 1 , x 2 , y 2 ∈ R x_1, y_1, x_2, y_2 \in \mathbb{R} x1,y1,x2,y2∈R),则
z 1 = z 2 ⇔ x 1 = x 2 且 y 1 = y 2 z_1 = z_2 \Leftrightarrow x_1 = x_2 \text{ 且 } y_1 = y_2 z1=z2⇔x1=x2 且 y1=y2
特别地 : x + y i = 0 ⇔ x = 0 x + yi = 0 \Leftrightarrow x = 0 x+yi=0⇔x=0 且 y = 0 y = 0 y=0。
注意:应用复数相等的充要条件时,必须确保各变量的实数性。
3. 复数的模
定义 :复数 z = x + y i z = x + yi z=x+yi 的模 (或模长)定义为
∣ z ∣ = x 2 + y 2 |z| = \sqrt{x^2 + y^2} ∣z∣=x2+y2
几何意义为向量 O Z → \overrightarrow{OZ} OZ 的长度。实数的绝对值是复数模在实轴上的特殊情形。
性质:
| 性质 | 公式 |
|---|---|
| 非负性 | ∣ z ∣ ≥ 0 |z| \geq 0 ∣z∣≥0,且 ∣ z ∣ = 0 ⇔ z = 0 |z| = 0 \Leftrightarrow z = 0 ∣z∣=0⇔z=0 |
| 对称性 | ∣ z ˉ ∣ = ∣ z ∣ |\bar{z}| = |z| ∣zˉ∣=∣z∣ |
| 乘积 | ∣ z 1 ⋅ z 2 ∣ = ∣ z 1 ∣ ⋅ ∣ z 2 ∣ |z_1 \cdot z_2| = |z_1| \cdot |z_2| ∣z1⋅z2∣=∣z1∣⋅∣z2∣ |
| 商 | ∣ z 1 z 2 ∣ = ∣ z 1 ∣ ∣ z 2 ∣ \left|\dfrac{z_1}{z_2}\right| = \dfrac{|z_1|}{|z_2|} z2z1 =∣z2∣∣z1∣( z 2 ≠ 0 z_2 \neq 0 z2=0) |
| 三角不等式 | ∣ ∣ z 1 ∣ − ∣ z 2 ∣ ∣ ≤ ∣ z 1 ± z 2 ∣ ≤ ∣ z 1 ∣ + ∣ z 2 ∣ \big||z_1| - |z_2|\big| \leq |z_1 \pm z_2| \leq |z_1| + |z_2| ∣z1∣−∣z2∣ ≤∣z1±z2∣≤∣z1∣+∣z2∣ |
说明:虽然复数本身不能比较大小,但复数的模为非负实数,可以比较大小。
三、复数的四则运算
设 z 1 = x 1 + y 1 i z_1 = x_1 + y_1 i z1=x1+y1i, z 2 = x 2 + y 2 i z_2 = x_2 + y_2 i z2=x2+y2i( x 1 , y 1 , x 2 , y 2 ∈ R x_1, y_1, x_2, y_2 \in \mathbb{R} x1,y1,x2,y2∈R)。
1. 加减法
法则 :
z 1 + z 2 = ( x 1 + x 2 ) + ( y 1 + y 2 ) i z 1 − z 2 = ( x 1 − x 2 ) + ( y 1 − y 2 ) i z_1 + z_2 = (x_1 + x_2) + (y_1 + y_2)i\\ z_1 - z_2 = (x_1 - x_2) + (y_1 - y_2)i z1+z2=(x1+x2)+(y1+y2)iz1−z2=(x1−x2)+(y1−y2)i
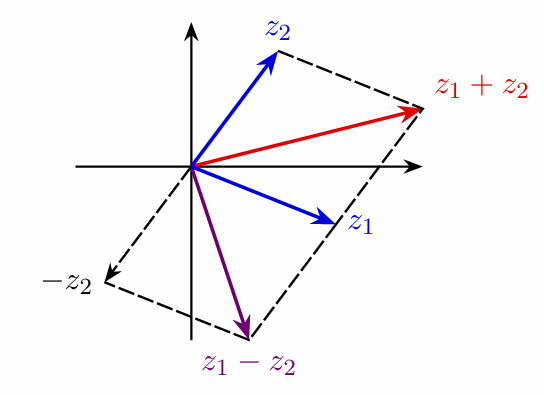
几何意义:复数的加减法运算与复平面上向量的加减法运算一致,满足平行四边形法则。
2. 乘法
法则 :
z 1 ⋅ z 2 = ( x 1 x 2 − y 1 y 2 ) + ( x 1 y 2 + x 2 y 1 ) i z_1 \cdot z_2 = (x_1x_2 - y_1y_2) + (x_1y_2 + x_2y_1)i z1⋅z2=(x1x2−y1y2)+(x1y2+x2y1)i
本质为多项式乘法结合 i 2 = − 1 i^2 = -1 i2=−1 化简。
3. 除法
法则 :设 z 2 ≠ 0 z_2 \neq 0 z2=0,则
z 1 z 2 = z 1 ⋅ z ˉ 2 z 2 ⋅ z ˉ 2 = x 1 x 2 + y 1 y 2 x 2 2 + y 2 2 + x 2 y 1 − x 1 y 2 x 2 2 + y 2 2 i \frac{z_1}{z_2} = \frac{z_1 \cdot \bar{z}_2}{z_2 \cdot \bar{z}_2} = \frac{x_1x_2 + y_1y_2}{x_2^2 + y_2^2} + \frac{x_2y_1 - x_1y_2}{x_2^2 + y_2^2}i z2z1=z2⋅zˉ2z1⋅zˉ2=x22+y22x1x2+y1y2+x22+y22x2y1−x1y2i
通过分子分母同乘分母的共轭复数,将分母实数化。
4. 运算律
复数的四则运算满足:
- 交换律 : z 1 + z 2 = z 2 + z 1 z_1 + z_2 = z_2 + z_1 z1+z2=z2+z1, z 1 ⋅ z 2 = z 2 ⋅ z 1 z_1 \cdot z_2 = z_2 \cdot z_1 z1⋅z2=z2⋅z1
- 结合律 : ( z 1 + z 2 ) + z 3 = z 1 + ( z 2 + z 3 ) (z_1 + z_2) + z_3 = z_1 + (z_2 + z_3) (z1+z2)+z3=z1+(z2+z3), ( z 1 ⋅ z 2 ) ⋅ z 3 = z 1 ⋅ ( z 2 ⋅ z 3 ) (z_1 \cdot z_2) \cdot z_3 = z_1 \cdot (z_2 \cdot z_3) (z1⋅z2)⋅z3=z1⋅(z2⋅z3)
- 分配律 : z 1 ⋅ ( z 2 + z 3 ) = z 1 ⋅ z 2 + z 1 ⋅ z 3 z_1 \cdot (z_2 + z_3) = z_1 \cdot z_2 + z_1 \cdot z_3 z1⋅(z2+z3)=z1⋅z2+z1⋅z3
四、复数的三角表示与指数形式
1. 三角形式
定义 :复数 z = x + y i z = x + yi z=x+yi 可表示为
z = r ( cos θ + i sin θ ) z = r(\cos\theta + i\sin\theta) z=r(cosθ+isinθ)
其中:
- r = ∣ z ∣ = x 2 + y 2 r = |z| = \sqrt{x^2 + y^2} r=∣z∣=x2+y2 称为模(到原点的距离)
- θ \theta θ 称为辐角 (与正实轴的夹角),满足 tan θ = y x \tan\theta = \dfrac{y}{x} tanθ=xy( x ≠ 0 x \neq 0 x=0)
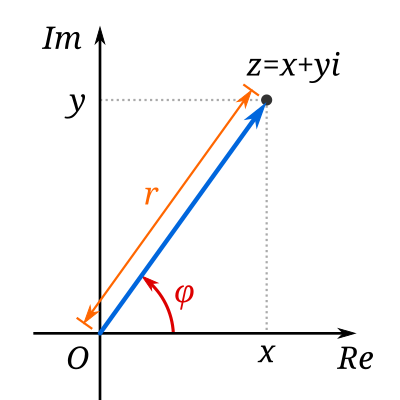
与代数形式的转换 :
x = r cos θ , y = r sin θ x = r\cos\theta, \quad y = r\sin\theta x=rcosθ,y=rsinθ
2. 辐角的主值
定义 :在区间 [ 0 , 2 π ) [0, 2\pi) [0,2π) 内的辐角称为辐角主值 ,记为 arg z \arg z argz。
| 符号 | 名称 | 取值范围 | 特点 |
|---|---|---|---|
| arg z \arg z argz | 辐角主值 | [ 0 , 2 π ) [0, 2\pi) [0,2π) 或 ( − π , π ] (-\pi, \pi] (−π,π] | 唯一,常用 |
| Arg z \operatorname{Arg} z Argz | 多值辐角 | arg z + 2 k π \arg z + 2k\pi argz+2kπ( k ∈ Z k \in \mathbb{Z} k∈Z) | 无穷多个值 |
各象限辐角主值范围:
| 位置 | arg z \arg z argz 的范围 |
|---|---|
| 第一象限 | ( 0 , π 2 ) \left(0, \dfrac{\pi}{2}\right) (0,2π) |
| 第二象限 | ( π 2 , π ) \left(\dfrac{\pi}{2}, \pi\right) (2π,π) |
| 第三象限 | ( π , 3 π 2 ) \left(\pi, \dfrac{3\pi}{2}\right) (π,23π) |
| 第四象限 | ( 3 π 2 , 2 π ) \left(\dfrac{3\pi}{2}, 2\pi\right) (23π,2π) |
| 正实轴 | 0 0 0 |
| 负实轴 | π \pi π |
计算公式 :
arg z = { arctan y x , x > 0 arctan y x + π , x < 0 , y ≥ 0 arctan y x − π , x < 0 , y < 0 π 2 , x = 0 , y > 0 − π 2 , x = 0 , y < 0 \arg z = \begin{cases} \arctan\dfrac{y}{x}, & x > 0 \\[6pt] \arctan\dfrac{y}{x} + \pi, & x < 0,\ y \geq 0 \\[6pt] \arctan\dfrac{y}{x} - \pi, & x < 0,\ y < 0 \\[6pt] \dfrac{\pi}{2}, & x = 0,\ y > 0 \\[6pt] -\dfrac{\pi}{2}, & x = 0,\ y < 0 \end{cases} argz=⎩ ⎨ ⎧arctanxy,arctanxy+π,arctanxy−π,2π,−2π,x>0x<0, y≥0x<0, y<0x=0, y>0x=0, y<0
示例:
| 复数 z z z | 辐角主值 arg z \arg z argz |
|---|---|
| 1 1 1 | 0 0 0 |
| i i i | π 2 \dfrac{\pi}{2} 2π |
| − 1 -1 −1 | π \pi π |
| − i -i −i | 3 π 2 \dfrac{3\pi}{2} 23π |
| 1 + i 1+i 1+i | π 4 \dfrac{\pi}{4} 4π |
与极坐标的关系
复数的三角形式 :
z = r ( cos θ + i sin θ ) = r e i θ z = r(\cos\theta + i\sin\theta) = re^{i\theta} z=r(cosθ+isinθ)=reiθ
其中:
- r = ∣ z ∣ = a 2 + b 2 r = |z| = \sqrt{a^2+b^2} r=∣z∣=a2+b2 是模(到原点的距离)
- θ = arg z \theta = \arg z θ=argz 是辐角(与正实轴的夹角)
示例
| 复数 z z z | 辐角主值 arg z \arg z argz |
|---|---|
| 1 1 1 | 0 0 0 |
| i i i | π 2 \dfrac{\pi}{2} 2π |
| − 1 -1 −1 | π \pi π |
| − i -i −i | 3 π 2 \dfrac{3\pi}{2} 23π(或 − π 2 -\dfrac{\pi}{2} −2π) |
| 1 + i 1+i 1+i | π 4 \dfrac{\pi}{4} 4π |
2. 辐角的主值
定义 :在区间 [ 0 , 2 π ) [0, 2\pi) [0,2π) 内的辐角称为辐角主值 ,记为 arg z \arg z argz。
各象限辐角主值范围:
| 象限 | arg z \arg z argz 的范围 |
|---|---|
| 第一象限 | ( 0 , π 2 ) \left(0, \dfrac{\pi}{2}\right) (0,2π) |
| 第二象限 | ( π 2 , π ) \left(\dfrac{\pi}{2}, \pi\right) (2π,π) |
| 第三象限 | ( π , 3 π 2 ) \left(\pi, \dfrac{3\pi}{2}\right) (π,23π) |
| 第四象限 | ( 3 π 2 , 2 π ) \left(\dfrac{3\pi}{2}, 2\pi\right) (23π,2π) |
| 正实轴 | 0 0 0 |
| 负实轴 | π \pi π |
3. 三角形式的乘除法
设 z 1 = r 1 ( cos θ 1 + i sin θ 1 ) z_1 = r_1(\cos\theta_1 + i\sin\theta_1) z1=r1(cosθ1+isinθ1), z 2 = r 2 ( cos θ 2 + i sin θ 2 ) z_2 = r_2(\cos\theta_2 + i\sin\theta_2) z2=r2(cosθ2+isinθ2)。
乘法 :
z 1 ⋅ z 2 = r 1 r 2 [ cos ( θ 1 + θ 2 ) + i sin ( θ 1 + θ 2 ) ] z_1 \cdot z_2 = r_1r_2[\cos(\theta_1 + \theta_2) + i\sin(\theta_1 + \theta_2)] z1⋅z2=r1r2[cos(θ1+θ2)+isin(θ1+θ2)]
法则:模相乘,辐角相加。
除法 :
z 1 z 2 = r 1 r 2 [ cos ( θ 1 − θ 2 ) + i sin ( θ 1 − θ 2 ) ] \frac{z_1}{z_2} = \frac{r_1}{r_2}[\cos(\theta_1 - \theta_2) + i\sin(\theta_1 - \theta_2)] z2z1=r2r1[cos(θ1−θ2)+isin(θ1−θ2)]
法则:模相除,辐角相减。
4. 棣莫弗定理
定理 :对任意整数 n ∈ Z n \in \mathbb{Z} n∈Z,
r ( cos θ + i sin θ ) \] n = r n ( cos n θ + i sin n θ ) \[r(\\cos\\theta + i\\sin\\theta)\]\^n = r\^n(\\cos n\\theta + i\\sin n\\theta) \[r(cosθ+isinθ)\]n=rn(cosnθ+isinnθ)
**特别地** ( r = 1 r = 1 r=1 时):
( cos θ + i sin θ ) n = cos n θ + i sin n θ (\\cos\\theta + i\\sin\\theta)\^n = \\cos n\\theta + i\\sin n\\theta (cosθ+isinθ)n=cosnθ+isinnθ
#### 5. 复数的开方
**n n n 次方根** :复数 r ( cos θ + i sin θ ) r(\\cos\\theta + i\\sin\\theta) r(cosθ+isinθ) 的 n n n 个 n n n 次方根为
r n ( cos θ + 2 k π n + i sin θ + 2 k π n ) , k = 0 , 1 , 2 , ... , n − 1 \\sqrt\[n\]{r}\\left(\\cos\\frac{\\theta + 2k\\pi}{n} + i\\sin\\frac{\\theta + 2k\\pi}{n}\\right), \\quad k = 0, 1, 2, \\ldots, n-1 nr (cosnθ+2kπ+isinnθ+2kπ),k=0,1,2,...,n−1
**n n n 次单位根** : 1 1 1 的 n n n 个 n n n 次方根为
ω k = cos 2 k π n + i sin 2 k π n , k = 0 , 1 , ... , n − 1 \\omega_k = \\cos\\frac{2k\\pi}{n} + i\\sin\\frac{2k\\pi}{n}, \\quad k = 0, 1, \\ldots, n-1 ωk=cosn2kπ+isinn2kπ,k=0,1,...,n−1
**性质**:
* n n n 个 n n n 次单位根在复平面内构成正 n n n 边形的顶点;
* 所有 n n n 次单位根之和为 0 0 0,即 ∑ k = 0 n − 1 ω k = 0 \\displaystyle\\sum_{k=0}\^{n-1} \\omega_k = 0 k=0∑n−1ωk=0。
#### 6. 指数形式(欧拉公式)
**欧拉公式** :
e i θ = cos θ + i sin θ e\^{i\\theta} = \\cos\\theta + i\\sin\\theta eiθ=cosθ+isinθ
**指数形式** :
z = r e i θ z = re\^{i\\theta} z=reiθ
**运算性质**:
* e i θ 1 ⋅ e i θ 2 = e i ( θ 1 + θ 2 ) e\^{i\\theta_1} \\cdot e\^{i\\theta_2} = e\^{i(\\theta_1 + \\theta_2)} eiθ1⋅eiθ2=ei(θ1+θ2)
* ( e i θ ) n = e i n θ (e\^{i\\theta})\^n = e\^{in\\theta} (eiθ)n=einθ
* e i θ 1 e i θ 2 = e i ( θ 1 − θ 2 ) \\dfrac{e\^{i\\theta_1}}{e\^{i\\theta_2}} = e\^{i(\\theta_1 - \\theta_2)} eiθ2eiθ1=ei(θ1−θ2)
**欧拉恒等式** :
e i π + 1 = 0 e\^{i\\pi} + 1 = 0 eiπ+1=0
此式联系了五个基本数学常数: e , i , π , 1 , 0 e, i, \\pi, 1, 0 e,i,π,1,0。
### 五、复数与方程
#### 1. 实系数一元二次方程
**定理** :实系数一元二次方程 a x 2 + b x + c = 0 ax\^2 + bx + c = 0 ax2+bx+c=0( a , b , c ∈ R , a ≠ 0 a, b, c \\in \\mathbb{R}, a \\neq 0 a,b,c∈R,a=0):
* 若 Δ = b 2 − 4 a c ≥ 0 \\Delta = b\^2 - 4ac \\geq 0 Δ=b2−4ac≥0,有两个实根;
* 若 Δ \< 0 \\Delta \< 0 Δ\<0,有一对**共轭虚根** :
x = − b ± − Δ i 2 a x = \\frac{-b \\pm \\sqrt{-\\Delta}i}{2a} x=2a−b±−Δ i
**性质**:实系数多项式方程的虚根成对出现,且互为共轭复数。
**因式分解**:在复数范围内,任意多项式都可分解为一次因式的乘积。
### 六、复数的几何意义与应用
#### 1. 常见轨迹
| 条件 | 轨迹 |
|:----------------------------------------------------------------------------------------------------------------------------------------------------------|:------------------------------|
| ∣ z − z 0 ∣ = r \|z - z_0\| = r ∣z−z0∣=r | 以 z 0 z_0 z0 为圆心, r r r 为半径的圆 |
| ∣ z − z 1 ∣ = ∣ z − z 2 ∣ \|z - z_1\| = \|z - z_2\| ∣z−z1∣=∣z−z2∣ | 线段 z 1 z 2 z_1z_2 z1z2 的垂直平分线 |
| ∣ z − z 1 ∣ + ∣ z − z 2 ∣ = 2 a \|z - z_1\| + \|z - z_2\| = 2a ∣z−z1∣+∣z−z2∣=2a( 2 a \> ∣ z 1 − z 2 ∣ 2a \> \|z_1 - z_2\| 2a\>∣z1−z2∣) | 椭圆 |
| ∣ ∣ z − z 1 ∣ − ∣ z − z 2 ∣ ∣ = 2 a \\big\|\|z - z_1\| - \|z - z_2\|\\big\| = 2a ∣z−z1∣−∣z−z2∣ =2a( 2 a \< ∣ z 1 − z 2 ∣ 2a \< \|z_1 - z_2\| 2a\<∣z1−z2∣) | 双曲线 |
| arg ( z − z 0 ) = θ \\arg(z - z_0) = \\theta arg(z−z0)=θ | 从 z 0 z_0 z0 出发的射线 |
#### 2. 最值问题解法
* **几何法** :利用 ∣ z − z 0 ∣ \|z - z_0\| ∣z−z0∣ 表示距离,结合图形求最值;
* **代数法** :设 z = x + y i z = x + yi z=x+yi 转化为函数最值;
* **三角法** :设 z = r ( cos θ + i sin θ ) z = r(\\cos\\theta + i\\sin\\theta) z=r(cosθ+isinθ) 利用有界性。
### 七、典型例题
#### 题型一:复数概念与命题判断
**例题** 判断下列命题的正误:
① 若 a ∈ R a \\in \\mathbb{R} a∈R,则 ( a + 1 ) i (a+1)i (a+1)i 是纯虚数;
② 若 a , b ∈ R a, b \\in \\mathbb{R} a,b∈R,且 a \> b a \> b a\>b,则 a + i \> b + i a + i \> b + i a+i\>b+i;
③ 若 ( x 2 − 4 ) + ( x 2 + 3 x + 2 ) i (x\^2 - 4) + (x\^2 + 3x + 2)i (x2−4)+(x2+3x+2)i 是纯虚数,则 x = ± 2 x = \\pm 2 x=±2;
④ 实数集是复数集的真子集。
**解析**:
| 命题 | 正误 | 说明 |
|:---|:--:|:-----------------------------------------------------------------|
| ① | ✗ | a = − 1 a = -1 a=−1 时, ( a + 1 ) i = 0 (a+1)i = 0 (a+1)i=0 不是纯虚数 |
| ② | ✗ | 两个虚数不能比较大小 |
| ③ | ✗ | x = − 2 x = -2 x=−2 时,结果为 0 0 0 不是纯虚数 |
| ④ | ✓ | 实数是虚部为 0 0 0 的特殊复数 |
**答案**:④正确。
#### 题型二:复数分类与参数求解
**例题** 当实数 m m m 为何值时, z = m 2 + m − 6 m + ( m 2 − 2 m ) i z = \\dfrac{m\^2 + m - 6}{m} + (m\^2 - 2m)i z=mm2+m−6+(m2−2m)i 为:
1. 实数?
2. 虚数?
3. 纯虚数?
**解**:
| 类型 | 条件 | 结果 |
|:----|:--------------------------------------------------------------------------------------------------------------------------------------------------------------|:--------------------------------------------|
| 实数 | { m 2 − 2 m = 0 m ≠ 0 \\begin{cases} m\^2 - 2m = 0 \\\\ m \\neq 0 \\end{cases} {m2−2m=0m=0 | m = 2 m = 2 m=2 |
| 虚数 | m 2 − 2 m ≠ 0 m\^2 - 2m \\neq 0 m2−2m=0 且 m ≠ 0 m \\neq 0 m=0 | m ≠ 0 m \\neq 0 m=0 且 m ≠ 2 m \\neq 2 m=2 |
| 纯虚数 | { m ≠ 0 m 2 + m − 6 m = 0 m 2 − 2 m ≠ 0 \\begin{cases} m \\neq 0 \\\\ \\dfrac{m\^2+m-6}{m} = 0 \\\\ m\^2 - 2m \\neq 0 \\end{cases} ⎩ ⎨ ⎧m=0mm2+m−6=0m2−2m=0 | m = − 3 m = -3 m=−3 |
#### 题型三:复数相等与方程组
**例题** 若 z 1 = − 3 − 4 i z_1 = -3 - 4i z1=−3−4i, z 2 = ( n 2 − 3 m − 1 ) + ( n 2 − m − 6 ) i z_2 = (n\^2 - 3m - 1) + (n\^2 - m - 6)i z2=(n2−3m−1)+(n2−m−6)i,且 z 1 = z 2 z_1 = z_2 z1=z2,求 m + n m + n m+n。
**解** :由复数相等条件:
{ n 2 − 3 m − 1 = − 3 n 2 − m − 6 = − 4 \\begin{cases} n\^2 - 3m - 1 = -3 \\\\ n\^2 - m - 6 = -4 \\end{cases} {n2−3m−1=−3n2−m−6=−4
解得 m = 2 , n = ± 2 m = 2, n = \\pm 2 m=2,n=±2,故 m + n = 4 m + n = 4 m+n=4 或 0 0 0。
#### 题型四:复数与对数综合
**例题** 若 log 2 ( x 2 − 3 x − 2 ) + i log 2 ( x 2 + 2 x + 1 ) \> 1 \\log_2(x\^2 - 3x - 2) + i\\log_2(x\^2 + 2x + 1) \> 1 log2(x2−3x−2)+ilog2(x2+2x+1)\>1,求 x x x。
**解** :复数大于实数说明该复数为实数且实部大于 1 1 1,虚部为 0 0 0:
{ log 2 ( x 2 − 3 x − 2 ) \> 1 log 2 ( x 2 + 2 x + 1 ) = 0 \\begin{cases} \\log_2(x\^2 - 3x - 2) \> 1 \\\\ \\log_2(x\^2 + 2x + 1) = 0 \\end{cases} {log2(x2−3x−2)\>1log2(x2+2x+1)=0
解得 x = − 2 x = -2 x=−2。
#### 题型五:复数的几何意义
**例题** 已知 z = ( a 2 − 1 ) + ( 2 a − 1 ) i z = (a\^2 - 1) + (2a - 1)i z=(a2−1)+(2a−1)i,求 a a a 的范围使点 Z Z Z 在第三象限。
**解** :
{ a 2 − 1 \< 0 2 a − 1 \< 0 ⇒ − 1 \< a \< 1 2 \\begin{cases} a\^2 - 1 \< 0 \\\\ 2a - 1 \< 0 \\end{cases} \\Rightarrow -1 \< a \< \\frac{1}{2} {a2−1\<02a−1\<0⇒−1\