和算行列式理论的起源与发展 | 从关孝和到江户时代的展开方法研究

斐夷所非2026-02-09 11:13

注：本文为 "和算行列式理论" 相关合辑。

图片清晰度受引文原图所限。

原文为繁体，略作重排，如有内容异常，请看原文。

和算中的行列式

Determinants in Wasan

国立台南第一高级中学 林仓亿 老师

Posted on 2014/08/09

(1)：创立者关孝和

(1): Seki Takakazu, the Originator

日本江户时代（1603-1867，即德川幕府时代）的数学家在吸纳中国传入的数学知识后，独立发展出诸多新理论与新算法，后世将该时期的数学体系称为「和算」，该时期的数学家则被称为「和算家」。关孝和是和算家中的代表性人物，被后世尊为「算圣」，也是世界上最早提出行列式相关算法的学者之一。

关孝和的生平记载留存较少，其出生年份是否为 1642 年，目前尚存争议；其逝世于 1708 年，这一史实已无异议。关孝和本姓内山，过继至关姓武士家族后改从关姓。他曾担任甲府宰相德川纲重及其子德川纲丰的家臣，任「勘定吟味役」一职，该职位的职能与会计总管相当。在德川纲丰成为德川将军的养子后，关孝和成为幕府直属武士，官至「御纳户组头」，主要负责幕府的器具管理事宜。关孝和的仕途无显著建树，终其一生以家臣身份为领主供职。

与平凡的仕途不同，关孝和的数学研究成果则彰显出卓越的学术价值。其生前正式出版的数学著作仅有 2 本：《发微算法》（1674 年）与《括要算法》（1712 年，逝后由其弟子整理出版），其余著作均以手抄本形式在和算家群体中流传，其中有 3 本著作可代表其数学研究的主要成就：

  1. 《解见题之法》：约成书于 1683 年，内容包含各类几何求积问题、圆锥曲线问题，以及现今所称的阿基米得螺线相关问题；
  2. 《解隐题之法》：成书于 1685 年，主要为开方术与方程论的相关内容；
  3. 《解伏题之法》：重订于 1683 年，主要阐述多元高次方程组的求解方法。

上述三本著作被后世合称为《三部抄》，是关孝和数学成就的集中体现。在《解伏题之法》中，关孝和为求解多元高次方程组，首次创立了与现今行列式算法等价的数学方法，后续和算家在该方法的基础上，将其推广至更高阶的行列式运算。数学史家徐泽林依据关孝和与其弟子建部贤明、建部贤弘合著的《大成算经》（1683-1711），将关孝和的数学成就归为八个方面：

  1. 创立「傍书法」，这是一种融合文字与算筹符号的代数表示方法；
  2. 提出高次代数方程式的数值求解方法；
  3. 建立消元算法与行列式展开的相关算法；
  4. 研究垛积招差术，推导各类级数相关公式；
  5. 探究不定方程的求解方法；
  6. 开展无穷小算法的相关研究；
  7. 进行几何学的相关探究；
  8. 开展组合分析的相关研究。

关孝和凭借其在数学领域的研究成果，吸引了众多学者追随其本人或其弟子研习数学，形成了和算发展中的「关流」，该流派成为江户时代和算的主流流派，对日本近代数学的发展产生了深远影响。部分日本数学史家将《发微算法》的出版年份 1674 年，视作日本数学脱离对中国数学的被动吸收与消化、开启自主发展的标志性节点。

(2)：关孝和的《解伏题之法》（上）

(2): Seki Takakazu's Kai Fukudai no Ho (Methods of Solving Secret Questions), Part 1

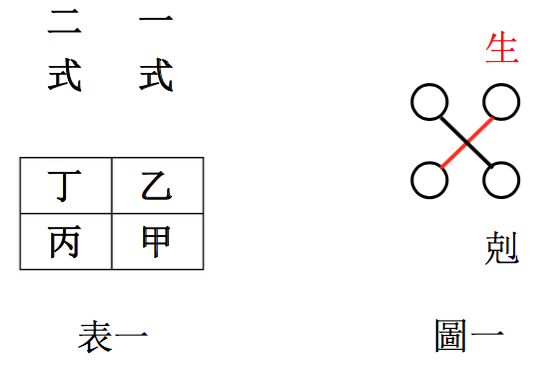
关孝和的《解伏题之法》（1683 年）以多元高次方程组的求解为基本内容，书中提出了求解多元高次方程组的六个步骤：真虚、两式、定乘、换式、生克、寄消。其中第五步「生克」，与现今行列式的展开过程等价，步骤中的「生」（以红色标注）与「克」（以黑色标注），用于确定行列式展开后各项的正负符号。以现今数学术语表述，关孝和在书中提出了与 2 至 5 阶行列式展开等价的方法，并推导写出 2 至 4 阶行列式的展开式。

以二阶行列式为例，关孝和采用表一的形式对其进行呈现，并称乙丙相乘为「生」，丁甲相乘为「克」。以现今数学符号表示，该展开规则为

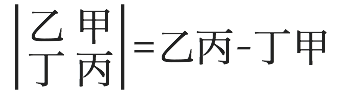
关孝和同时采用图一对该规则进行几何化表示：

同理，关孝和对三阶行列式的表示方法与现今的三阶行列式定义等价，其形式为

相关表述可见表二与图二：

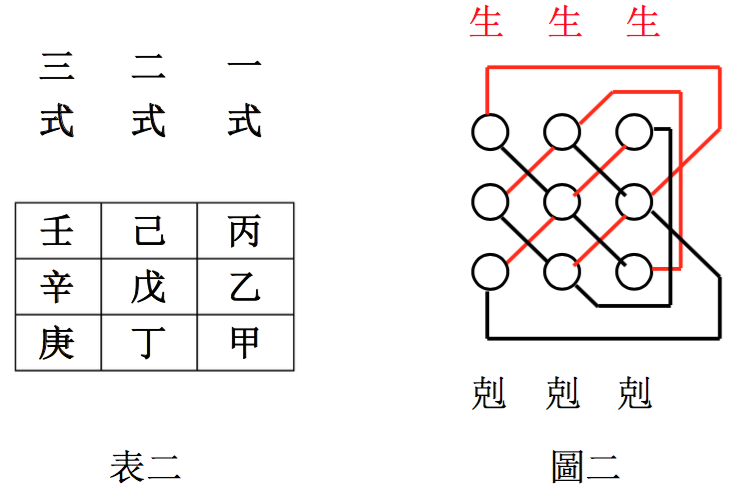
按照关孝和所定的「生」「克」规则，三阶行列式的展开式为：
丙戊庚 + 己辛甲 + 壬乙丁 − 丙辛丁 − 己乙庚 − 壬戊甲 丙戊庚 + 己辛甲 + 壬乙丁 - 丙辛丁 - 己乙庚 - 壬戊甲 丙戊庚+己辛甲+壬乙丁−丙辛丁−己乙庚−壬戊甲

该结果与现今三阶行列式的展开结果完全一致。

对于四阶行列式的展开，关孝和所提出的方法更为复杂，需先确定元素相乘的顺序，再依据该顺序判定各项的「生」「克」属性。尽管其推导的四阶行列式展开结果正确，但该方法无法推广至 5 阶及以上的行列式运算，即关孝和所提出的行列式展开方法存在适用范围的局限，本文对此不再作详细阐述。

综上，关孝和在《解伏题之法》中确已提出与现今行列式概念高度相似的数学思想，且该思想并非源于多元一次联立方程组的求解，而是从多元高次方程组的求解过程中发展而来。以下以二元二次方程组为例，对该思想的形成过程进行阐释，所举方程组为：
{ a 1 x 2 + b 1 x y + c 1 y 2 + d 1 x + e 1 y + f 1 = 0 a 2 x 2 + b 2 x y + c 2 y 2 + d 2 x + e 2 y + f 2 = 0 a 3 x 2 + b 3 x y + c 3 y 2 + d 3 x + e 3 y + f 3 = 0 \begin{cases} a_1 x^2 + b_1 xy + c_1 y^2 + d_1 x + e_1 y + f_1 = 0\\ a_2 x^2 + b_2 xy + c_2 y^2 + d_2 x + e_2 y + f_2 = 0\\ a_3 x^2 + b_3 xy + c_3 y^2 + d_3 x + e_3 y + f_3 = 0 \end{cases} ⎩ ⎨ ⎧a1x2+b1xy+c1y2+d1x+e1y+f1=0a2x2+b2xy+c2y2+d2x+e2y+f2=0a3x2+b3xy+c3y2+d3x+e3y+f3=0

第一步，将上述方程组视作以 x x x 为未知数的一元二次方程组，按 x x x 的升幂排列整理可得：
{ ( c 1 y 2 + e 1 y + f 1 ) + ( b 1 y + d 1 ) x + a 1 x 2 = 0 ( c 2 y 2 + e 2 y + f 2 ) + ( b 2 y + d 2 ) x + a 2 x 2 = 0 ( c 3 y 2 + e 3 y + f 3 ) + ( b 3 y + d 3 ) x + a 3 x 2 = 0 \begin{cases} (c_1 y^2 + e_1 y + f_1) + (b_1 y + d_1)x + a_1 x^2 = 0\\ (c_2 y^2 + e_2 y + f_2) + (b_2 y + d_2)x + a_2 x^2 = 0\\ (c_3 y^2 + e_3 y + f_3) + (b_3 y + d_3)x + a_3 x^2 = 0 \end{cases} ⎩ ⎨ ⎧(c1y2+e1y+f1)+(b1y+d1)x+a1x2=0(c2y2+e2y+f2)+(b2y+d2)x+a2x2=0(c3y2+e3y+f3)+(b3y+d3)x+a3x2=0

第二步，将整理后方程组的各项系数依次用甲、乙、...、庚表示，所得形式为

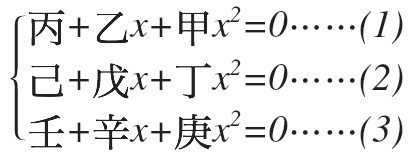
该形式即关孝和在书中所称的一式、二式、三式，显然，甲、乙、...、庚均为关于未知数 y y y 的多项式。

第三步，利用加减消元法消去方程组中的 x x x 项与 x 2 x^2 x2 项：

  1. 将一式乘以戊庚、二式乘以甲辛、三式乘以乙丁，所得三个式子为「生」，形式为
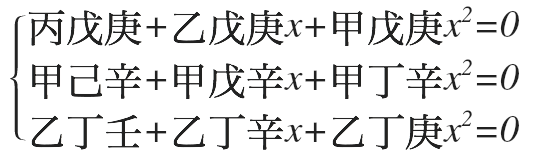
  1. 将一式乘以丁辛、二式乘以乙庚、三式乘以甲戊，所得三个式子为「克」，形式为

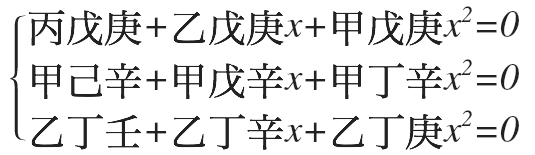
将「生」「克」对应的式子相消，可得等式：
丙戊庚 + 甲己辛 + 乙丁壬 − 丙丁辛 − 乙己庚 − 甲戊壬 = 0 丙戊庚 + 甲己辛 + 乙丁壬 - 丙丁辛 - 乙己庚 - 甲戊壬 = 0 丙戊庚+甲己辛+乙丁壬−丙丁辛−乙己庚−甲戊壬=0

该等式即为行列式

的展开结果。需注意，此处的甲、乙、...、庚均为关于未知数 y y y 的多项式，因此上述行列式展开后所得的等式为关于 y y y 的方程式。求解该方程式可得 y y y 的值，将 y y y 的值代回原方程组即可求得 x x x 的值。求解 y y y 的近似值的方法在当时被称为「开方术」，是和算家必备的数学方法，关孝和对此方法已熟练掌握。

以上为关孝和发展出与现今行列式概念相似的数学思想的简要阐释，其研究中体现的巧思与逻辑洞察力令人叹服。尽管其提出的行列式展开方法无法适用于 5 阶及以上的行列式运算，但这一局限并未影响其作为行列式理论先驱的学术地位。从数学发展的角度来看，这一方法的局限也为后续和算家提供了研究切入点，促使后世学者提出适用于高阶行列式的展开方法，相关内容将在后续文章中予以介绍。

(3)：关孝和的《解伏题之法》（下）

(3): Seki Takakazu's Kai Fukudai no Ho (Methods of Solving Secret Questions), Part 2

《 (2)：关孝和的《解伏题之法》（上）》中阐释了关孝和如何从多元高次方程组的求解过程中，发展出与现今行列式概念相似的数学思想。即便在现今的数学体系中，多元高次方程组的求解仍属于具有挑战性的问题，由此可见关孝和在数学领域的深厚造诣。以下通过 4 个实例，对关孝和的方法进行具体应用，同时指出该方法在部分场景中存在无法直接求解的情形。

例 1

求解方程组：
{ ( x − 1 ) 2 + ( y − 1 ) 2 = 1 ( x − 2 ) 2 + ( y − 2 ) 2 = 5 ( x − 3 ) 2 + ( y − 3 ) 2 = 13 \begin{cases} (x - 1)^2 + (y - 1)^2 = 1\\ (x - 2)^2 + (y - 2)^2 = 5\\ (x - 3)^2 + (y - 3)^2 = 13 \end{cases} ⎩ ⎨ ⎧(x−1)2+(y−1)2=1(x−2)2+(y−2)2=5(x−3)2+(y−3)2=13

关孝和的方法 ：

将方程组整理为以 x x x 为未知数的一元二次形式：
{ ( y 2 − 2 y + 1 ) − 2 x + x 2 = 0 ( y 2 − 4 y + 3 ) − 4 x + x 2 = 0 ( y 2 − 6 y + 5 ) − 6 x + x 2 = 0 \begin{cases} (y^2 - 2y + 1) - 2x + x^2 = 0\\ (y^2 - 4y + 3) - 4x + x^2 = 0\\ (y^2 - 6y + 5) - 6x + x^2 = 0 \end{cases} ⎩ ⎨ ⎧(y2−2y+1)−2x+x2=0(y2−4y+3)−4x+x2=0(y2−6y+5)−6x+x2=0

构造该方程组系数对应的行列式并令其等于 0：
∣ y 2 − 2 y + 1 − 2 1 y 2 − 4 y + 3 − 4 1 y 2 − 6 y + 5 − 6 1 ∣ = 0 \begin{vmatrix} y^2 - 2y + 1 & -2 & 1\\ y^2 - 4y + 3 & -4 & 1\\ y^2 - 6y + 5 & -6 & 1 \end{vmatrix} = 0 y2−2y+1y2−4y+3y2−6y+5−2−4−6111 =0

将该行列式展开后，各项相互抵消，得到恒等式 0 = 0 0=0 0=0，而非关于 y y y 的方程式，因此无法通过该方法直接求解 y y y 的值。

几何意义 ：

方程组中的三个方程式对应的图形均为圆形，其圆心依次为 ( 1 , 1 ) (1,1) (1,1)、 ( 2 , 2 ) (2,2) (2,2)、 ( 3 , 3 ) (3,3) (3,3)，半径依次为 1 1 1、 5 \sqrt{5} 5 、 13 \sqrt{13} 13 ，图形如下：

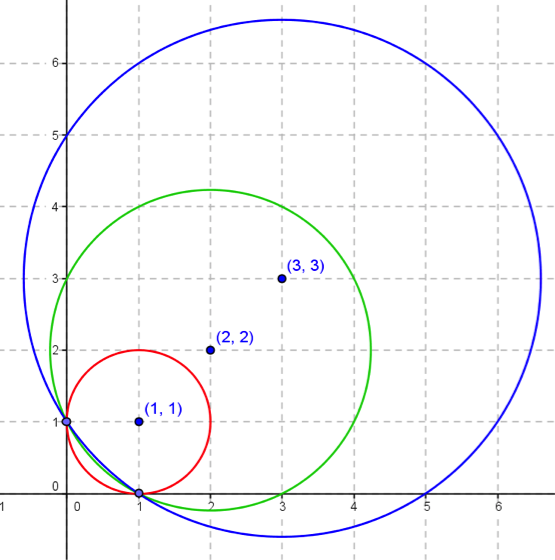
三个圆的交点为 ( 1 , 0 ) (1,0) (1,0) 与 ( 0 , 1 ) (0,1) (0,1)，因此方程组的两组解为 ( x , y ) = ( 1 , 0 ) (x,y)=(1,0) (x,y)=(1,0)、 ( x , y ) = ( 0 , 1 ) (x,y)=(0,1) (x,y)=(0,1)。

例 2

求解方程组：
{ ( x − 1 ) 2 + ( y − 1 ) 2 = 1 x 2 + y 2 = 1 ( x + 1 ) 2 + ( y + 1 ) 2 = 1 \begin{cases} (x - 1)^2 + (y - 1)^2 = 1\\ x^2 + y^2 = 1\\ (x + 1)^2 + (y + 1)^2 = 1 \end{cases} ⎩ ⎨ ⎧(x−1)2+(y−1)2=1x2+y2=1(x+1)2+(y+1)2=1

关孝和的方法 ：

将方程组整理为以 x x x 为未知数的一元二次形式：
{ ( y 2 − 2 y + 1 ) − 2 x + x 2 = 0 ( y 2 − 1 ) + 0 x + x 2 = 0 ( y 2 + 2 y + 1 ) + 2 x + x 2 = 0 \begin{cases} (y^2 - 2y + 1) - 2x + x^2 = 0\\ (y^2 - 1) + 0x + x^2 = 0\\ (y^2 + 2y + 1) + 2x + x^2 = 0 \end{cases} ⎩ ⎨ ⎧(y2−2y+1)−2x+x2=0(y2−1)+0x+x2=0(y2+2y+1)+2x+x2=0

构造该方程组系数对应的行列式并令其等于 0：
∣ y 2 − 2 y + 1 − 2 1 y 2 − 1 0 1 y 2 + 2 y + 1 2 1 ∣ = 0 \begin{vmatrix} y^2 - 2y + 1 & -2 & 1\\ y^2 - 1 & 0 & 1\\ y^2 + 2y + 1 & 2 & 1 \end{vmatrix} = 0 y2−2y+1y2−1y2+2y+1−202111 =0

将该行列式展开后得到等式 8 = 0 8=0 8=0，该等式显然不成立，因此原方程组无解。

几何意义 ：

方程组中的三个方程式对应的图形均为圆形，其圆心依次为 ( 1 , 1 ) (1,1) (1,1)、 ( 0 , 0 ) (0,0) (0,0)、 ( − 1 , − 1 ) (-1,-1) (−1,−1)，半径均为 1 1 1，图形如下：

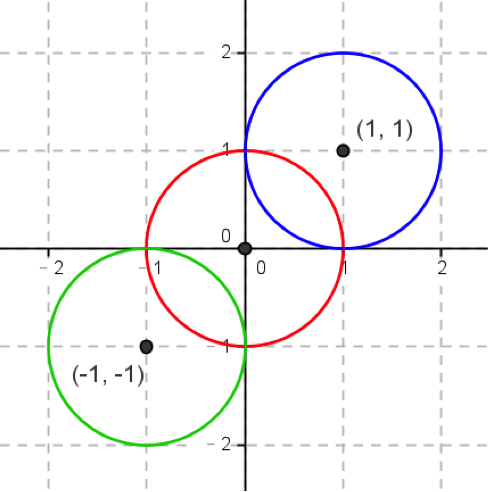
三个圆无公共交点，因此原方程组无解。

例 3

求解方程组：
{ x 2 + y 2 = 1 4 x 2 + y 2 − 4 = 0 y 2 − 4 x + 4 = 0 \begin{cases} x^2 + y^2 = 1\\ 4x^2 + y^2 - 4 = 0\\ y^2 - 4x + 4 = 0 \end{cases} ⎩ ⎨ ⎧x2+y2=14x2+y2−4=0y2−4x+4=0

关孝和的方法 ：

将方程组整理为以 x x x 为未知数的一元二次形式：
{ ( y 2 − 1 ) + 0 x + x 2 = 0 ( y 2 − 4 ) + 0 x + 4 x 2 = 0 ( y 2 + 4 ) − 4 x + 0 x 2 = 0 \begin{cases} (y^2 - 1) + 0x + x^2 = 0\\ (y^2 - 4) + 0x + 4x^2 = 0\\ (y^2 + 4) - 4x + 0x^2 = 0 \end{cases} ⎩ ⎨ ⎧(y2−1)+0x+x2=0(y2−4)+0x+4x2=0(y2+4)−4x+0x2=0

构造该方程组系数对应的行列式并令其等于 0：
∣ y 2 − 1 0 1 y 2 − 4 0 4 y 2 + 4 − 4 0 ∣ = 0 \begin{vmatrix} y^2 - 1 & 0 & 1\\ y^2 - 4 & 0 & 4\\ y^2 + 4 & -4 & 0 \end{vmatrix} = 0 y2−1y2−4y2+400−4140 =0

将该行列式展开后解得：
12 y 2 = 0 ⇒ y = 0 12y^2 = 0 \Rightarrow y = 0 12y2=0⇒y=0

将 y = 0 y=0 y=0 代回原方程组，解得 x = 1 x=1 x=1，因此原方程组的解为 ( x , y ) = ( 1 , 0 ) (x,y)=(1,0) (x,y)=(1,0)。

几何意义 ：

方程组中的三个方程式对应的图形依次为圆形、椭圆、抛物线，三者的公共交点为 ( 1 , 0 ) (1,0) (1,0)，图形如下：

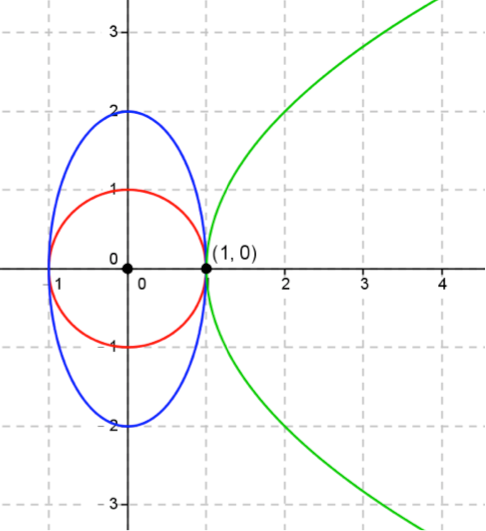
因此原方程组的唯一解为 ( x , y ) = ( 1 , 0 ) (x,y)=(1,0) (x,y)=(1,0)。

例 4

求解方程组：
{ x 2 + y 2 = 1 4 x 2 + y 2 − 4 = 0 y 2 − 4 x + 8 = 0 \begin{cases} x^2 + y^2 = 1\\ 4x^2 + y^2 - 4 = 0\\ y^2 - 4x + 8 = 0 \end{cases} ⎩ ⎨ ⎧x2+y2=14x2+y2−4=0y2−4x+8=0

关孝和的方法 ：

将方程组整理为以 x x x 为未知数的一元二次形式：
{ ( y 2 − 1 ) + 0 x + x 2 = 0 ( y 2 − 4 ) + 0 x + 4 x 2 = 0 ( y 2 + 8 ) − 4 x + 0 x 2 = 0 \begin{cases} (y^2 - 1) + 0x + x^2 = 0\\ (y^2 - 4) + 0x + 4x^2 = 0\\ (y^2 + 8) - 4x + 0x^2 = 0 \end{cases} ⎩ ⎨ ⎧(y2−1)+0x+x2=0(y2−4)+0x+4x2=0(y2+8)−4x+0x2=0

构造该方程组系数对应的行列式并令其等于 0：
∣ y 2 − 1 0 1 y 2 − 4 0 4 y 2 + 8 − 4 0 ∣ = 0 \begin{vmatrix} y^2 - 1 & 0 & 1\\ y^2 - 4 & 0 & 4\\ y^2 + 8 & -4 & 0 \end{vmatrix} = 0 y2−1y2−4y2+800−4140 =0

将该行列式展开后解得：
12 y 2 = 0 ⇒ y = 0 12y^2 = 0 \Rightarrow y = 0 12y2=0⇒y=0

将 y = 0 y=0 y=0 代回原方程组，解得 x = 1 x=1 x=1，但将 ( x , y ) = ( 1 , 0 ) (x,y)=(1,0) (x,y)=(1,0) 代入第三个方程式 y 2 − 4 x + 8 = 0 y^2 - 4x + 8 = 0 y2−4x+8=0 时，等式不成立，因此原方程组无解。

几何意义 ：

方程组中的三个方程式对应的图形依次为圆形、椭圆、抛物线，三者无公共交点，图形如下：

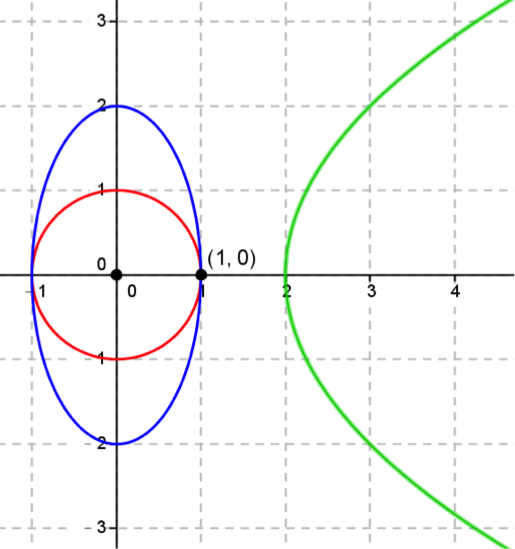
因此原方程组无解。

由上述 4 个实例可得出结论：通过构造系数行列式并令其等于 0 的方法，未必能推导出关于 y y y 的有效方程式；即便能推导出该方程式并求解得到 x x x、 y y y 的值，也需将其代回原方程组进行检验，检验不成立的解需予以舍弃。

该现象的成因可从关孝和方法的本质进行分析：将多元高次方程组整理为

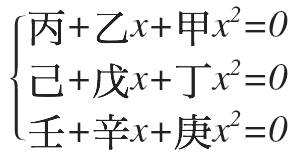
的形式后，若将 x 2 x^2 x2 视作新的变量 y ′ y' y′，则原方程组可转化为关于 x x x 与 y ′ y' y′ 的二元一次方程组。根据二元一次方程组存在公共解的条件，可推导出其系数行列式需满足

值得注意的是，这一推导思路与莱布尼兹发展行列式概念的思路高度一致，相关内容可参见本网站《行列式的滥觞：莱布尼兹 (1)、(2)》。东西方行列式理论的开创者，在研究思路上形成了跨地域的契合。

但该方法存在本质局限： y ′ = x 2 y'=x^2 y′=x2 并非与 x x x 相互独立的变量，因此通过上述系数行列式求得的解，必须代回原方程组进行检验，排除检验不成立的解。

简言之，多元高次方程组的解的存在性与解的个数，随方程式的数量变化而变化，其求解过程也随未知数个数与方程式次数的增加而趋于复杂。例如，当方程组中的未知数个数多于 2 个时，需通过多次消元逐步减少未知数的个数。

关孝和与其弟子建部贤明、建部贤弘合著的《大成算经》中，记载了一道与四元四次方程组等价的问题，该四元四次方程组为：
{ x 1 4 + x 2 3 + x 3 + x 4 = A 1 x 1 3 + x 2 2 + x 3 3 + x 4 4 = A 2 x 1 2 + x 2 + x 3 4 + x 4 3 = A 3 x 1 + x 2 4 + x 3 2 + x 4 2 = A 4 \begin{cases} x_1^4 + x_2^3 + x_3 + x_4 = A_1\\ x_1^3 + x_2^2 + x_3^3 + x_4^4 = A_2\\ x_1^2 + x_2 + x_3^4 + x_4^3 = A_3\\ x_1 + x_2^4 + x_3^2 + x_4^2 = A_4 \end{cases} ⎩ ⎨ ⎧x14+x23+x3+x4=A1x13+x22+x33+x44=A2x12+x2+x34+x43=A3x1+x24+x32+x42=A4

该问题的原文记载如下，可供有研究兴趣的读者参考求解：

假如有甲乙丙丁平方各一。甲云：甲方三乘幂[注：四次方 ]、乙方再乘幂[注：三次方 ]、丙方、丁方相并共若干；乙云：甲方再乘幂、乙方幂[注：二次方 ]、丙方再乘幂、丁方三乘幂相并共若干；丙云：甲方幂、乙方、丙方三乘幂、丁方再乘幂相并共若干；丁云：甲方、乙方三乘幂、丙方幂、丁方幂相并共若干。问甲方？

(4)：降级展开法

(4): The Reductive Algorithm

关孝和提出与现今行列式等价的求解方法后，吸引诸多和算家展开后续研究，后世学者不仅修正了关孝和方法中的局限------该方法应用于 5 阶及以上行列式时，求解结果存在偏差，还提出了多种新的行列式展开方法。本文将介绍其中的「降级展开法」，该方法与现今高中数学课堂中所称的「范德蒙（Vandermonde, 1735-1796，法国）展开法」等价。

目前可考的文献中，最早记载该展开方法的学者为井关知辰（Izeki Tomotoki）。井关知辰在其 1690 年所著的《算法发挥》上卷中，将行列式命名为「阳率」，将行列式的展开结果命名为「阴率」。例如，「平阳率」「立阳率」「三阳率」分别对应 2 阶、3 阶、4 阶行列式，「平阴率」「立阴率」「三阴率」则分别对应 2 阶、3 阶、4 阶行列式的展开式。井关知辰在书中还记载了「四阳率」与「四阴率」，即 5 阶行列式及其展开式，并阐述了适用于更高阶「阳率」的展开方法。

上图为井关知辰《算法发挥》中关于「立阳率」与「立阴率」的记载内容。将其转化为横式并以英文字母表示行列式元素，形式为：

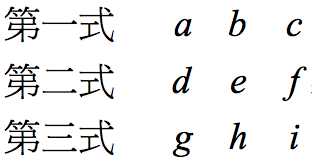
该展开方法的要点可参考上图左上方的 3 个 3 × 3 3\times 3 3×3 方格，其本质即为现今的降级展开法，将该部分放大后如下：

该部分内容阐释了从「立阳率」推导「立阴率」的具体步骤，以现今的数学符号表示，该步骤为：

  • a ⋅ ∣ e f h i ∣ − b ⋅ ∣ d f g i ∣ + c ⋅ ∣ d e g h ∣ +a \cdot \begin{vmatrix} e & f\\ h & i \end{vmatrix} -b \cdot \begin{vmatrix} d & f\\ g & i \end{vmatrix} +c \cdot \begin{vmatrix} d & e\\ g & h \end{vmatrix} +a⋅ ehfi −b⋅ dgfi +c⋅ dgeh

日本京都大学图书馆的网页中收录了《算法发挥》的全本图片，有研究兴趣的读者可查阅原文，了解井关知辰如何通过降级展开法推导更高阶行列式的展开式。以下仅呈现书中关于「三阴率」（4 阶行列式展开式）的书页内容：

从该内容可看出，井关知辰先将 4 阶行列式展开为 4 个 3 阶行列式，再将每个 3 阶行列式按「立阴率」的规则展开，最终得到 4 阶行列式的展开式，共包含 4 × 6 = 24 4\times6=24 4×6=24 项。

关孝和于 1683 年提出的行列式展开方法存在适用范围局限，而井关知辰在 7 年后的 1690 年，便在其著作中提出了适用于高阶行列式的降级展开法。目前尚无定论的是，井关知辰与关流之间是否存在学术往来。事实上，井关知辰的生卒年份至今未被考证，但从其行列式研究以高次方程式求解为背景这一特征可推测，其或许与关流存在学术交流，或通过其他途径获知关孝和的研究成果，并在此基础上展开后续研究。此外，同期和算家田中由真在其《双式定格术》中，也记载了与井关知辰一致的降级展开法；关流则在《大成算经》（关孝和、建部贤明、建部贤弘，1683-1711）中修正了关孝和原方法的局限，所采用的同样是降级展开法。由此可见，行列式的展开方法在当时已成为和算家的重要研究主题，吸引了诸多学者展开探索。除降级展开法外，和算家还提出了其他行列式展开方法，相关内容将在后续文章中予以介绍。

(5)：拉普拉斯展开法

(5): Laplace Expansion

关孝和之后，和算家对行列式展开方法的研究取得了进一步发展。除前文介绍的井关知辰外，久留岛义太（Kurushima Yoshihiro,?-1757）也是该领域的重要学者，其提出的行列式展开方法与现今所称的「拉普拉斯（Pierre-Simon Laplace, 1749-1827，法国）展开法」等价。

久留岛义太为自学成才的和算家，其数学知识并非源于师门传授，而是通过研读《新篇尘劫记》自主习得；后续其与当时的和算家展开广泛学术交流，尤其与关流和算家的交流，丰富了其研究主题，开拓了新的研究领域，对后世和算的发展产生了深远影响。因此，久留岛义太与关孝和、建部贤弘并称为日本三大和算家。据史料记载，久留岛义太性情放达，虽数学造诣深厚，却未形成专属的学术流派，其著作也未正式出版，仅以稿本形式在和算家群体中传抄，逝后留下《久氏遗书》一部。

《久氏遗书》中的《算学粹沙》篇，以 3 阶至 6 阶行列式为研究对象，探讨其展开方法并提出了新的求解思路。以 4 阶行列式为例，久留岛义太提出的展开方法与现今的拉普拉斯展开法等价，其形式为：

其在书中的具体表述为：

若将书中「东夏内去南春」等表述转化为现今的行列式符号，形式为：

则久留岛义太提出的展开方法可表示为：

该方法即为现今所称的拉普拉斯展开法。

拉普拉斯展开法中，展开式各项前的正负符号由其行序置换的次数决定：置换次数为偶数时，该项前取「 + + +」；置换次数为奇数时，该项前取「 − - −」。

以

为例，该项元素的行序依次为 2、4、1、3，将该排列置换为标准排列 1、2、3、4，最少需要 3 次对换： 2413 ⇒ 1423 ⇒ 1243 ⇒ 1234 2413\Rightarrow1423\Rightarrow1243\Rightarrow1234 2413⇒1423⇒1243⇒1234（对换方法不唯一），置换次数为奇数，因此该项前取「 − - −」。

置换次数与逆序数的数值相等，逆序数的定义为：在一个排列中，若较小的数字出现在较大数字的右侧，该组合即为一个逆序，排列中逆序的总数即为逆序数。

对排列 2413 进行逆序数计算：2 在 1 左侧，构成 1 个逆序；4 在 1、3 左侧，构成 2 个逆序，因此该排列的逆序数为 1 + 2 = 3 1+2=3 1+2=3，与置换次数一致。

再以

为例，该项元素的行序依次为 2、3、1、4，其逆序数为 2，置换次数为偶数，因此该项前取「 + + +」。

以下以 5 阶行列式为例，对拉普拉斯展开法进行具体应用，该 5 阶行列式为：
∣ 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 ∣ \begin{vmatrix} 1 & 2 & 3 & 4 & 5\\ 6 & 7 & 8 & 9 & 10\\ 11 & 12 & 13 & 14 & 15\\ 16 & 17 & 18 & 19 & 20\\ 21 & 22 & 23 & 24 & 25 \end{vmatrix} 16111621271217223813182349141924510152025

按拉普拉斯展开法对其进行展开，结果为：

∣ 1 2 6 7 ∣ ⋅ ∣ 13 14 15 18 19 20 23 24 25 ∣    −    ∣ 1 3 6 8 ∣ ⋅ ∣ 12 14 15 17 19 20 22 24 25 ∣    +    ∣ 1 4 6 9 ∣ ⋅ ∣ 12 13 15 17 18 20 22 23 25 ∣    −    ∣ 1 5 6 10 ∣ ⋅ ∣ 12 13 14 17 18 19 22 23 24 ∣ +    ∣ 2 3 7 8 ∣ ⋅ ∣ 11 14 15 16 19 20 21 24 25 ∣    −    ∣ 2 4 7 9 ∣ ⋅ ∣ 11 13 15 16 18 20 21 23 25 ∣    +    ∣ 2 5 7 10 ∣ ⋅ ∣ 11 13 14 16 18 19 21 23 24 ∣ −    ∣ 3 4 8 9 ∣ ⋅ ∣ 11 12 15 16 17 20 21 22 25 ∣    +    ∣ 3 5 8 10 ∣ ⋅ ∣ 11 12 14 16 17 19 21 22 24 ∣    −    ∣ 4 5 9 10 ∣ ⋅ ∣ 11 12 13 16 17 18 21 22 23 ∣ \small \begin{aligned} &\begin{vmatrix} 1&2\\ 6&7 \end{vmatrix} \cdot \begin{vmatrix} 13&14&15\\ 18&19&20\\ 23&24&25 \end{vmatrix} \;-\; \begin{vmatrix} 1&3\\ 6&8 \end{vmatrix} \cdot \begin{vmatrix} 12&14&15\\ 17&19&20\\ 22&24&25 \end{vmatrix} \;+\; \begin{vmatrix} 1&4\\ 6&9 \end{vmatrix} \cdot \begin{vmatrix} 12&13&15\\ 17&18&20\\ 22&23&25 \end{vmatrix} \;-\; \begin{vmatrix} 1&5\\ 6&10 \end{vmatrix} \cdot \begin{vmatrix} 12&13&14\\ 17&18&19\\ 22&23&24 \end{vmatrix} \\[12pt] &\quad +\; \begin{vmatrix} 2&3\\ 7&8 \end{vmatrix} \cdot \begin{vmatrix} 11&14&15\\ 16&19&20\\ 21&24&25 \end{vmatrix} \;-\; \begin{vmatrix} 2&4\\ 7&9 \end{vmatrix} \cdot \begin{vmatrix} 11&13&15\\ 16&18&20\\ 21&23&25 \end{vmatrix} \;+\; \begin{vmatrix} 2&5\\ 7&10 \end{vmatrix} \cdot \begin{vmatrix} 11&13&14\\ 16&18&19\\ 21&23&24 \end{vmatrix} \\[12pt] &\quad -\; \begin{vmatrix} 3&4\\ 8&9 \end{vmatrix} \cdot \begin{vmatrix} 11&12&15\\ 16&17&20\\ 21&22&25 \end{vmatrix} \;+\; \begin{vmatrix} 3&5\\ 8&10 \end{vmatrix} \cdot \begin{vmatrix} 11&12&14\\ 16&17&19\\ 21&22&24 \end{vmatrix} \;-\; \begin{vmatrix} 4&5\\ 9&10 \end{vmatrix} \cdot \begin{vmatrix} 11&12&13\\ 16&17&18\\ 21&22&23 \end{vmatrix} \end{aligned} 1627 ⋅ 131823141924152025 − 1638 ⋅ 121722141924152025 + 1649 ⋅ 121722131823152025 − 16510 ⋅ 121722131823141924 + 2738 ⋅ 111621141924152025 − 2749 ⋅ 111621131823152025 + 27510 ⋅ 111621131823141924 − 3849 ⋅ 111621121722152025 + 38510 ⋅ 111621121722141924 − 49510 ⋅ 111621121722131823

若对拉普拉斯展开法仍有探究兴趣，可参考久留岛义太在书中记载的 6 阶行列式展开实例，其形式为：

读者可尝试以 3 阶行列式的乘积形式，推导该 6 阶行列式的展开式。

参考资料

  1. 徐泽林 (2012). 《和算中源：和算算法及其中算源流》，上海：上海交通大学出版社。
  2. 徐泽林、周畅、夏青 (2013). 《建部贤弘的数学思想》，北京：科学出版社。
  3. 梁宗巨、王青建、孙宏安 (1995). 《世界数学通史》，沈阳：辽宁教育出版社。
  4. 杨浩菊 (2004). 《行列式理论历史研究》，西北大学博士论文。
  5. 林典蔚 (2012). 《关孝和〈三部抄〉之内容分析》，国立台湾师范大学硕士论文。

via：

热门推荐
01GitHub 镜像站点02Claude Code + GLM4.7 避坑指南：解决 Unable to connect to Anthropic services03openclaw配置教程（linux+局域网ollama）04UV安装并设置国内源05AI 规范驱动开发“三剑客”深度对比：Spec-Kit、Kiro 与 OpenSpec 实战指南06Linux下V2Ray安装配置指南07Claude Code Skills 实用使用手册08openclaw使用nginx反代部署过程 与disconnected (1008): pairing required解决09Vue-skills的中文文档10OpenClaw Chrome扩展使用教程 - 浏览器中继控制