吉布斯现象 | 频域有限性与时域振荡的矛盾

注：本文为 "吉布斯现象" 相关合辑。

图片清晰度受引文原图所限。

略作重排，未整理去重。

如有内容异常，请看原文。

---

吉布斯现象

Wreng 我是 002 于 2021‑09‑17 22:08:58 发布

本文对吉布斯现象的定义、产生机理进行阐述，并分析通过频域窗函数对该现象进行抑制的方法。

1 吉布斯现象的定义

时域不连续信号的完备表示需要无穷多频率分量，而实际信号处理系统仅能获取有限频率范围，即对信号频谱实施频率截断 。

频率截断会导致时域信号在不连续点附近产生振荡，该现象定义为吉布斯现象。

定义：对具有无穷频率分量的信号实施频率截断，使其在时域不连续处出现振荡的现象称为吉布斯现象。

• 连续时间周期信号可展开为傅里叶级数，取前有限项可得到原信号的最小均方误差逼近。当项数趋于无穷时，该逼近在均方意义下收敛于原信号，但不满足一致收敛。在信号跳变点附近，傅里叶级数部分和会出现波动；若信号通过理想低通滤波器，则等效于频谱截断，呈现相同特性。
• 吉布斯现象的产生满足两个条件：
  1. 信号频谱被锐截止；
  2. 原信号存在跳变点。

2 吉布斯现象的产生机理

吉布斯现象的直接诱因是频率截断 。

频率截断可由截止频率为 ω c \omega_c ωc 的理想低通滤波器表征，其幅频与相频特性如下：

幅频特性	相频特性

理想低通滤波器仅保留 ∣ ω ∣ ≤ ω c |\omega|\le\omega_c ∣ω∣≤ωc 的频率分量，信号高频成分被滤除，高频信息丢失会在时域形成相应畸变。

下面分别分析理想低通滤波器对单位阶跃信号、矩形脉冲信号及周期矩形脉冲信号的响应，以揭示吉布斯现象的形成规律。

2.1 理想低通滤波器的单位阶跃响应

理想低通滤波器的频率响应为
H ( j ω ) = G 2 ω c ( ω ) e − j ω t d H (j\omega)=G_{2\omega_c}(\omega) e^{-j\omega t_d} H(jω)=G2ωc(ω)e−jωtd

其对单位阶跃信号 u ( t ) u (t) u(t) 的响应频谱为
S ( j ω ) = H ( j ω ) ⋅ F { u ( t ) } = G 2 ω c ( ω ) e − j ω t d ⋅ [ π δ ( ω ) + 1 j ω ] \begin {aligned} S (j\omega) &= H (j\omega)\cdot\mathcal {F}\{u (t)\} \\ &= G_{2\omega_c}(\omega) e^{-j\omega t_d}\cdot\left [\pi\delta (\omega)+\frac {1}{j\omega}\right] \end {aligned} S(jω)=H(jω)⋅F{u(t)}=G2ωc(ω)e−jωtd⋅[πδ(ω)+jω1]

对 S ( j ω ) S (j\omega) S(jω) 做傅里叶逆变换，得到时域输出：
s ( t ) = F − 1 { S ( j ω ) } = 1 2 π ∫ − ω c ω c [ π δ ( ω ) + 1 j ω ] e − j ω t d e j ω t d ω = 1 2 + 1 2 π ∫ − ω c ω c 1 j ω cos ⁡ [ ω ( t − t d ) ] d ω + 1 2 π ∫ − ω c ω c 1 ω sin ⁡ [ ω ( t − t d ) ] d ω = 1 2 + 1 π ∫ 0 ω c 1 ω sin ⁡ [ ω ( t − t d ) ] d ω = 1 2 + 1 π ∫ 0 ω c ( t − t d ) sin ⁡ x x d x \begin {aligned} s (t) &=\mathcal {F}^{-1}\{S (j\omega)\}\\ &=\frac {1}{2\pi}\int_{-\omega_c}^{\omega_c} \left [\pi\delta (\omega)+\frac {1}{j\omega}\right] e^{-j\omega t_d} e^{j\omega t}\mathrm {d}\omega\\ &=\frac {1}{2}+\frac {1}{2\pi}\int_{-\omega_c}^{\omega_c}\frac {1}{j\omega}\cos\left [\omega (t-t_d)\right]\mathrm {d}\omega +\frac {1}{2\pi}\int_{-\omega_c}^{\omega_c}\frac {1}{\omega}\sin\left [\omega (t-t_d)\right]\mathrm {d}\omega\\ &=\frac {1}{2}+\frac {1}{\pi}\int_{0}^{\omega_c}\frac {1}{\omega}\sin\left [\omega (t-t_d)\right]\mathrm {d}\omega\\ &=\frac {1}{2}+\frac {1}{\pi}\int_{0}^{\omega_c (t-t_d)}\frac {\sin x}{x}\mathrm {d} x \end {aligned} s(t)=F−1{S(jω)}=2π1∫−ωcωc[πδ(ω)+jω1]e−jωtdejωtdω=21+2π1∫−ωcωcjω1cos[ω(t−td)]dω+2π1∫−ωcωcω1sin[ω(t−td)]dω=21+π1∫0ωcω1sin[ω(t−td)]dω=21+π1∫0ωc(t−td)xsinxdx

式中积分项为正弦积分。输出时域波形如图所示：

理想低通滤波器的单位阶跃响应

该波形具有如下特征：

1. 输出存在吉布斯波纹 ，振荡频率为 2 π ω c 2\pi\omega_c 2πωc；
2. 上升沿前出现最大负向峰值（预冲 ），上升沿后出现最大正向峰值（过冲 ）。只要 ω c < ∞ \omega_c<\infty ωc<∞，过冲与预冲幅度约为稳态值的 9 % 9\% 9%；
3. 上升沿时间 t r = 2 π ω c t_r=\dfrac {2\pi}{\omega_c} tr=ωc2π， ω c \omega_c ωc 越大，上升沿越陡，吉布斯波纹振荡越密集；当 ω c → ∞ \omega_c\to\infty ωc→∞ 时，输出趋近于理想阶跃。

2.2 理想低通滤波器对矩形脉冲信号的响应

矩形脉冲信号可表示为两个阶跃信号之差：
G τ ( t ) = u ( t ) − u ( t − τ ) G_\tau (t)=u (t)-u (t-\tau) Gτ(t)=u(t)−u(t−τ)

其输出为两个阶跃响应的差值，因此同样存在吉布斯现象。

2.3 理想低通滤波器对周期矩形脉冲信号的响应

设周期方波周期 T = 2 τ T=2\tau T=2τ，基波角频率 Ω = π τ \Omega=\dfrac {\pi}{\tau} Ω=τπ，信号可表示为
f ( t ) = 2 G τ ( t ) ∗ δ 2 τ ( t ) − 1 f (t)=2G_\tau (t)*\delta_{2\tau}(t)-1 f(t)=2Gτ(t)∗δ2τ(t)−1

其频谱为
F ( j ω ) = 2 τ   S a ( τ ω 2 ) Ω   δ Ω ( ω ) − 2 π δ ( ω ) = ∑ n = − ∞ n ≠ 0 + ∞ 2 π   S a ( n π 2 ) δ ( ω − n Ω ) \begin {aligned} F (j\omega) &= 2\tau\,\mathrm {Sa}\left (\frac {\tau\omega}{2}\right)\Omega\,\delta_\Omega (\omega)-2\pi\delta (\omega) \\ &= \sum_{\substack {n=-\infty\\n\neq 0}}^{+\infty} 2\pi\,\mathrm {Sa}\left (\frac {n\pi}{2}\right)\delta (\omega-n\Omega) \end {aligned} F(jω)=2τSa(2τω)ΩδΩ(ω)−2πδ(ω)=n=−∞n=0∑+∞2πSa(2nπ)δ(ω−nΩ)
F ( j ω ) F (j\omega) F(jω) 为实偶函数，且仅含奇次谐波。经理想低通滤波（仅保留 ∣ ω ∣ < ω c |\omega|<\omega_c ∣ω∣<ωc 分量）后：

1. 若 ω c ≫ Ω \omega_c\gg\Omega ωc≫Ω，输出波形与原信号近似，但在不连续点存在预冲与过冲；
2. 随 ω c \omega_c ωc 减小，上升沿变缓，吉布斯波纹周期增大；
3. 若 ω c \omega_c ωc 接近 Ω \Omega Ω，输出退化为频率为 Ω \Omega Ω 的正弦波。

3 吉布斯现象的抑制方法

1. 频域加窗由有限窗宽引入吉布斯波纹，可采用非矩形窗（如三角窗等）替代理想锐截止窗。
2. 时域截断同样会引入吉布斯波纹，需选取合适的窗函数以降低振荡幅度。

---

吉布斯效应 (Gibbs)、振铃 (ring) 现象和块效应 (Blocking Artifact)

MAUM 于 2019‑07‑20 18:35:48 发布

一维信号中的吉布斯效应

一维信号范畴内，吉布斯效应的物理机理可通过系统理论完成清晰阐释。

吉布斯效应的定义

对包含不连续点的周期函数（如矩形脉冲信号）进行傅里叶级数展开，选取有限项展开式实现波形重构，该过程会产生吉布斯效应。选取的展开项数逐步增加时，重构波形的峰值会向原信号不连续点位置趋近；当展开项数取值足够大时，该峰值收敛于恒定值，数值约为信号总跳变值的 9%。

百度百科配套示意图如下：

吉布斯效应的直观表征

上述示意图的直观表征能力有限，故引用技术文献配套示意图：

采用有限项正弦函数与余弦函数构成的傅里叶级数，逼近非平滑的棱角型曲线时，信号幅值突变位置会产生吉布斯效应，具体表现为波形局部凸起。

二维信号中的振铃效应

二维图像信号中，振铃效应发生于灰度值剧烈突变的区域。频域滤波过程中采用理想低通滤波器时，图像低频分量被完整保留，高频分量被完全滤除；经逆变换完成图像重构后，空间域会产生类 sinc 函数的周期性震荡分量。理想低通滤波器在实现图像模糊处理的同时，该类震荡分量会分布于整幅重构图像，进而形成振铃效应。

百度百科中振铃效应的配套示意图如下：

图中红色圈注区域为振铃效应的典型表现区域。

振铃效应与块效应的实验验证

通过构建实验图像完成振铃效应与块效应的直观表征：将原始图像划分为 4×4 规格的子图像块，各子图像边沿区域存在像素灰度跳变；对每块子图像滤除 95% 的高频分量后，实施图像重构操作。

实验结果表明：红色圈注的脸部区域存在显著震荡细纹，该细纹由图像右侧头发区域的横向灰度剧烈突变引发；黄色圈注的子图像边缘位置，因相邻子图像频谱特性存在差异，滤波重构后的子图像边沿无法实现平滑衔接，进而形成块效应。

---

吉布斯现象产生的原因 --- 兼论谁先发现吉布斯现象的？

新屋熊 发布于 2024-02-03 19:18・美国

1 历史沿革

1807 年 12 月 21 日 ，傅里叶（Joseph Fourier）向法兰西科学院（Institut de France）提交题为《关于热在固体中的传播》（Mémoire sur la propagation de la chaleur dans les corps solides）的论文，首次系统提出：任意连续周期信号均可由一组适当的正弦曲线叠加表示。该观点遭到评审委员拉格朗日（Joseph-Louis Lagrange）的反对，未能通过审核。拉格朗日反对的理由是：傅里叶级数无法精确拟合具有棱角（即不连续点）的信号。

受当时学术权威的影响，该论文直至拉格朗日去世 15 年后（1822 年），才由傅里叶自行整理并以专著《热的解析理论》（Théorie analytique de la chaleur）形式出版。拉格朗日的观点具有合理性，但傅里叶理论并非错误 ------ 从理论层面而言，当采用无穷多组正弦曲线逼近带有棱角的信号时，可实现无限逼近，且逼近精度可达到能量无差别的程度。

1898 年 ，美国物理学家阿尔伯特・迈克尔逊（Albert Abraham Michelson，以发明迈克尔逊干涉仪闻名，该实验为 19 世纪物理学 "第一朵乌云" 及相对论的诞生埋下伏笔）研制了一台谐波分析仪。在测试方波信号时，他惊奇地发现：方波的有限项傅里叶级数 X N ( t ) X_N (t) XN(t)（其中 N N N 为傅里叶级数项数）在不连续点附近出现振荡起伏，且该起伏的峰值幅度似乎不随 N N N 增大而衰减。迈克尔逊遂致信著名数学物理学家约西亚・威拉德・吉布斯（Josiah Willard Gibbs）。吉布斯核查了这一结果，随即发表观点：随着 N N N 增加，部分起伏向不连续点压缩，但对于任意有限的 N N N 值，起伏的峰值幅度保持不变。值得注意的是，吉布斯于 1863 年获得耶鲁大学颁发的工程学博士学位，成为美国首位获此学位者。

然而，所谓 "吉布斯现象" 理应称为 "威布拉汉姆现象"（Wilbraham phenomenon） 。英国数学家亨利・威布拉汉姆（Henry Wilbraham）实际上早在1848 年即已发现该现象 [1]。1906 年，美国数学家马克西姆・博歇（Maxime Bôcher）在分析过冲（overshoot）问题的论文 [2] 中将此现象命名为 "吉布斯现象"，此后这一名称便沿用至今。

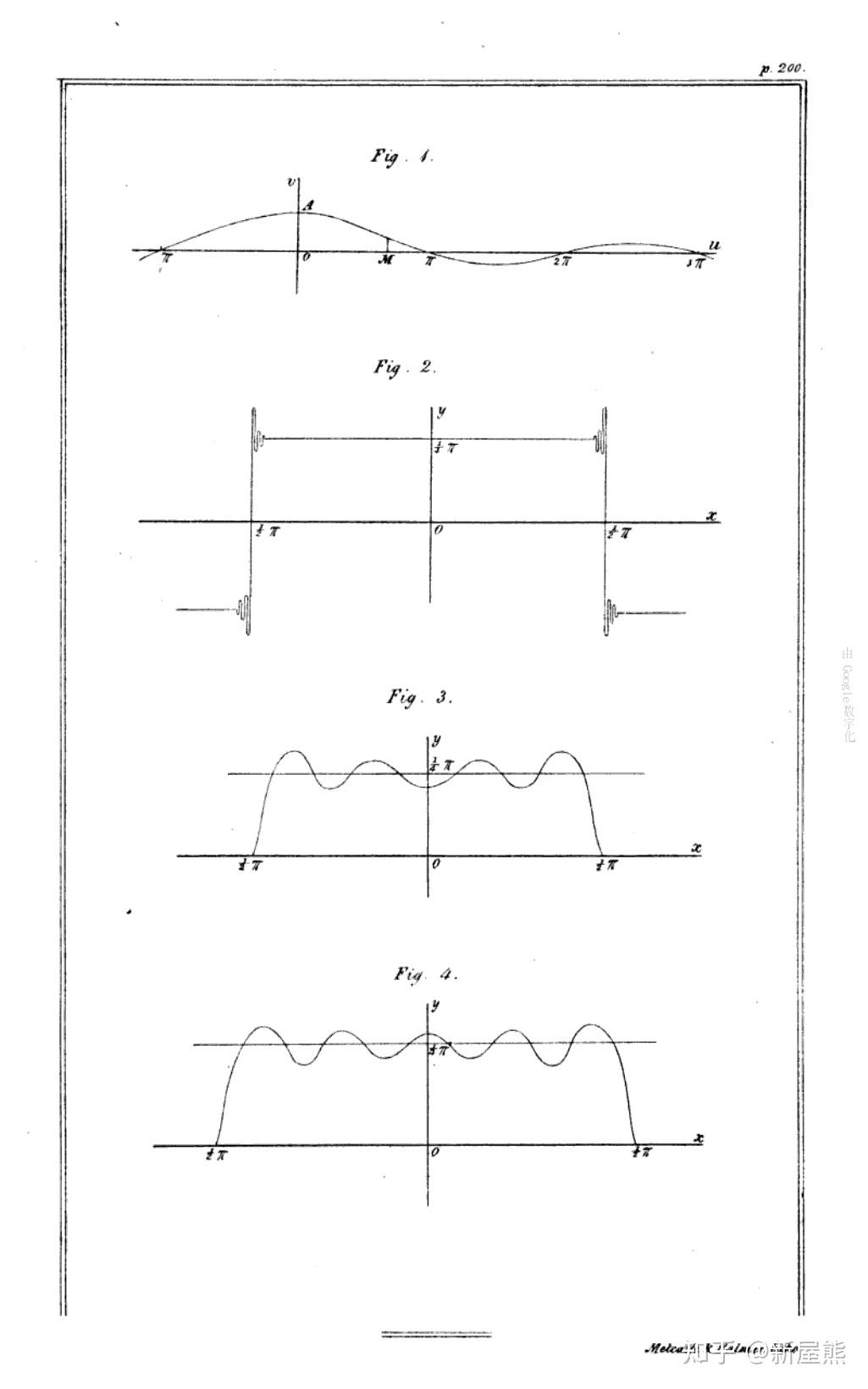
图 1 威布拉汉姆 1848 年的论文就已分析了所谓的 "吉布斯" 现象

1\] Wilbraham, Henry (1848) "On a certain periodic function", The Cambridge and Dublin Mathematical Journal, 3 : 198--201. \[2\] Bôcher, Maxime (April 1906) "Introduction to the theory of Fourier's series", Annals of Mathethematics, second series, 7 (3) : 81--152. The Gibbs phenomenon is discussed on pages 123--132; Gibbs's role is mentioned on page 129. ### 2 威布拉汉姆 - 吉布斯现象 威布拉汉姆 - 吉布斯现象是指，在处理具有不连续点的周期信号时，通过傅里叶级数展开并选取有限项进行合成所出现的特定现象。该现象具体表现为：随着所选傅里叶级数项数 N N N 的增加，合成波形会逐渐逼近原始信号，但在不连续点附近会出现固定高度的过冲。该过冲的最大值约为原信号不连续点处跳变值的 9%，且过冲不仅存在于不连续点本身，还会在其两侧呈现衰减振荡的分布形式。 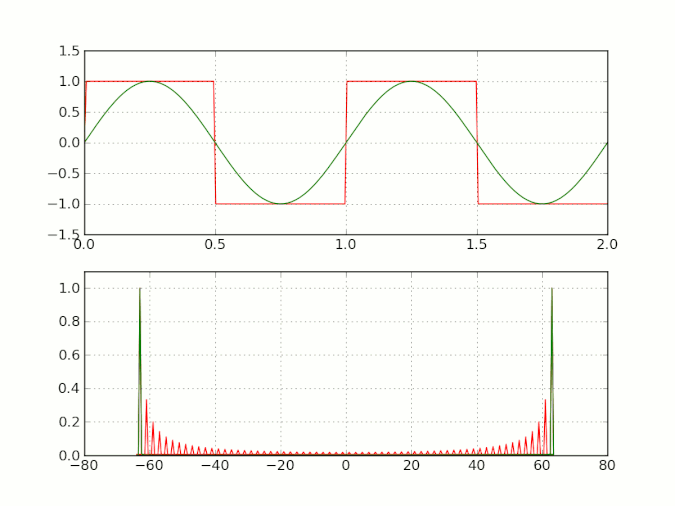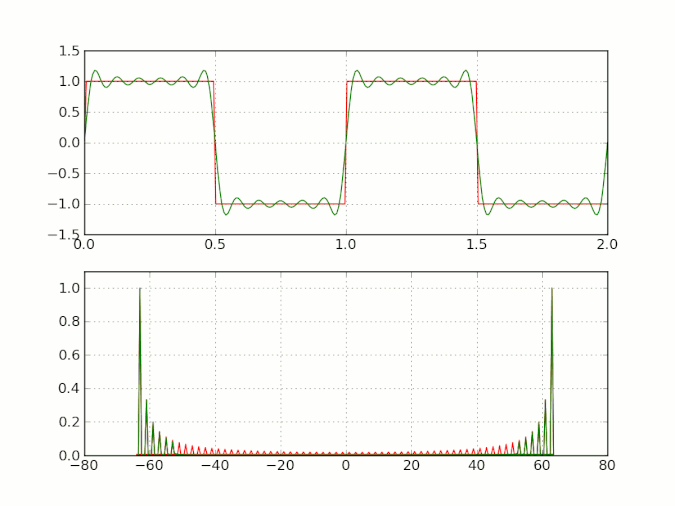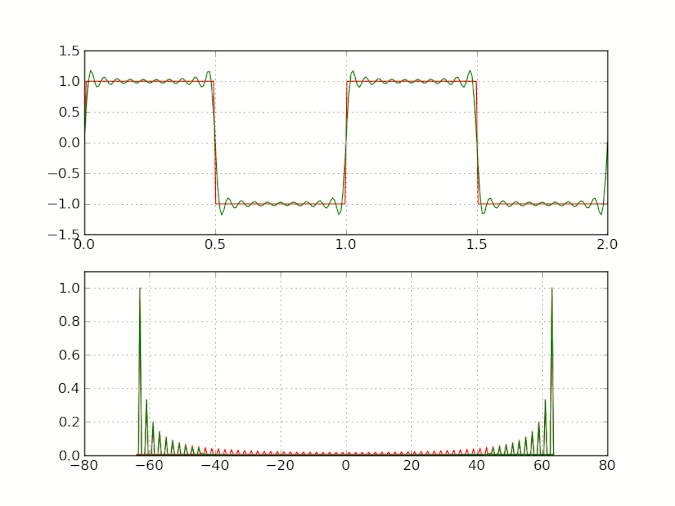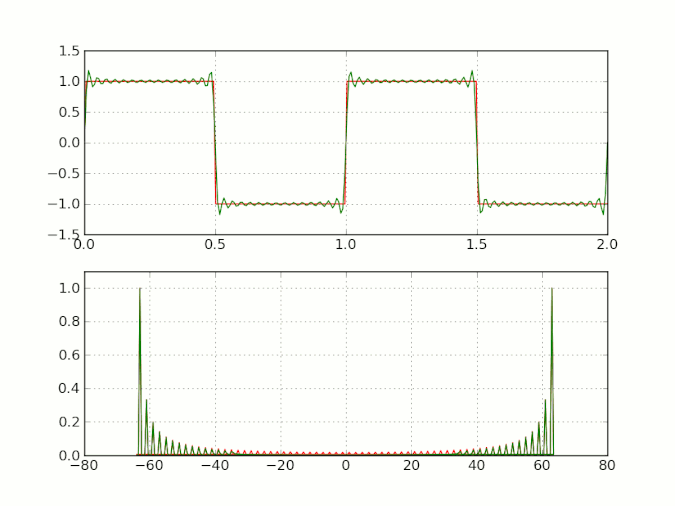 图 2 一个方波（周期为 1，峰对峰振幅为 2，取值范围为 -1 至 1）的加性合成动画，其谐波数不断增加。当谐波数较大时，围绕跳变不连续点振荡的威布拉汉姆 - 吉布斯现象会愈发明显 \[3\]。 \[3\] [https://en.wikipedia.org/wiki/Gibbs_phenomenon#cite_note-10](https://link.zhihu.com/?target=https://en.wikipedia.org/wiki/Gibbs_phenomenon#cite_note-10) ### 3 威布拉汉姆 - 吉布斯现象产生的原因 为便于理解，本节尽量避免使用复杂公式进行推导。 根据傅里叶变换理论，任意信号均可分解为一系列正弦波的叠加。对于单频正弦波，其表达式为 A sin ⁡ ω t A \\sin\\omega t Asinωt，其频域频谱为单一频率的线状谱；对于时域上无穷小的冲击响应 δ ( t ) \\delta (t) δ(t)，其频谱则覆盖整个频域直至无穷大。对于带有棱角的不连续信号（如矩形脉冲信号），由于其转角处存在 90 度棱角，在时域上等效于冲击响应 δ ( t ) \\delta (t) δ(t)，因此采用傅里叶级数拟合时，需要无穷多项傅里叶级数（即 N → ∞ N \\to \\infty N→∞）才能实现精准拟合。 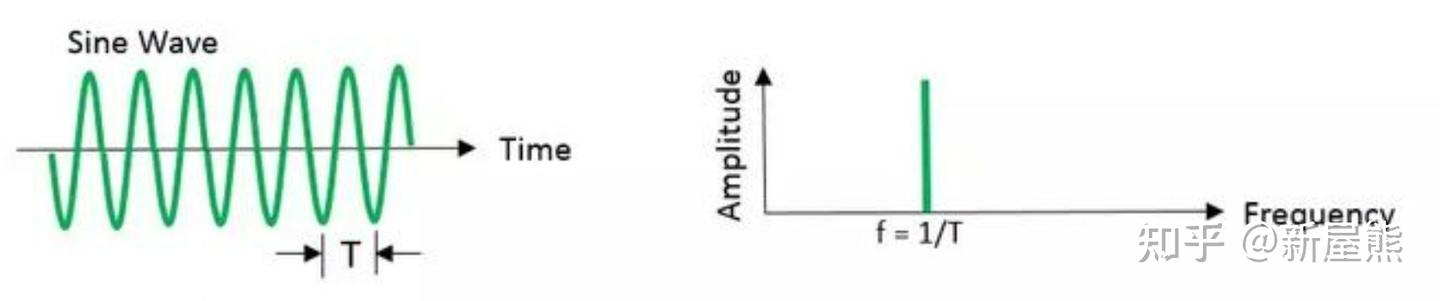 图 3 单频正弦波的时频变换： − ∞ -\\infty −∞ 至 + ∞ +\\infty +∞ 时间上无始无终的单频正弦波在频域上仅为单个频率分量  图 4 冲击响应 δ ( t ) \\delta (t) δ(t) 的时频变换：时间持续时间为 0（ Δ t → 0 \\Delta t \\to 0 Δt→0）的单个冲击响应，其频域包含从 − ∞ -\\infty −∞ 至 + ∞ +\\infty +∞ 的所有频率分量 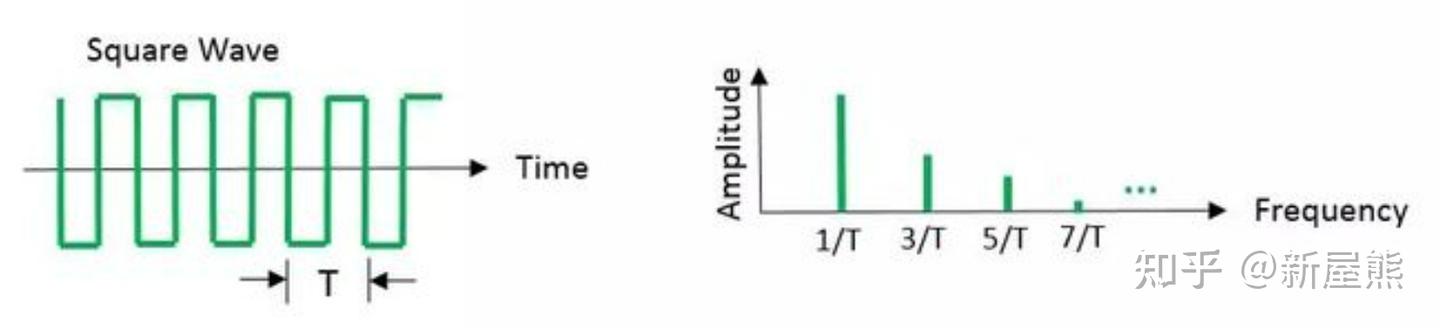 图 5 周期矩形脉冲信号的时频变换：包含符合傅里叶级数定义的无穷多个谐波频率 如前所述，带有棱角的信号需要无穷多项傅里叶级数才能实现精准拟合，即需要无穷多的高频分量参与拟合。但在实际工程应用中，无法选取无穷多项傅里叶级数（ N ≠ ∞ N \\neq \\infty N=∞），只能选取有限项（ N = K N=K N=K），这就意味着需要舍弃部分高频分量。因此，拟合得到的波形与原始波形存在偏差，且该偏差主要集中在信号的棱角位置，即不连续点附近。 下文将进一步分析威布拉汉姆 - 吉布斯现象在原始信号棱角位置出现震荡式快速衰减的具体原因。 #### 3.1 利用理想低通滤波器分析威布拉汉姆 - 吉布斯现象 时域的单位阶跃信号通过理想低通滤波器（截止频率为 ω c \\omega_c ωc）后，其时域波形的数学表达式如下（略去数学推导过程，直接给出结果）： s ( t ) = 1 2 + 1 π ∫ 0 ω c ( t − t d ) sin ⁡ x x d x \\begin {align} s (t)\&=\\frac {1}{2}+\\frac {1}{\\pi}\\int_{0}\^{\\omega_c (t-t_d)}\\frac {\\sin x}{x} \\mathrm{d}x\\tag {1} \\end {align} s(t)=21+π1∫0ωc(t−td)xsinxdx(1) 其中， t d t_d td 为阶跃信号的延迟时间（delay time），指阶跃信号从输入到系统产生响应的时间间隔。（为何采用理想低通滤波器分析威布拉汉姆 - 吉布斯现象？其与前文所述威布拉汉姆 - 吉布斯现象的解释存在何种关联？可结合前文内容自行思考。） s ( t ) s (t) s(t) 的波形特征由 sin ⁡ x x \\frac {\\sin x}{x} xsinx 的定积分结果决定，该积分结果的具体形式如图 6 所示。 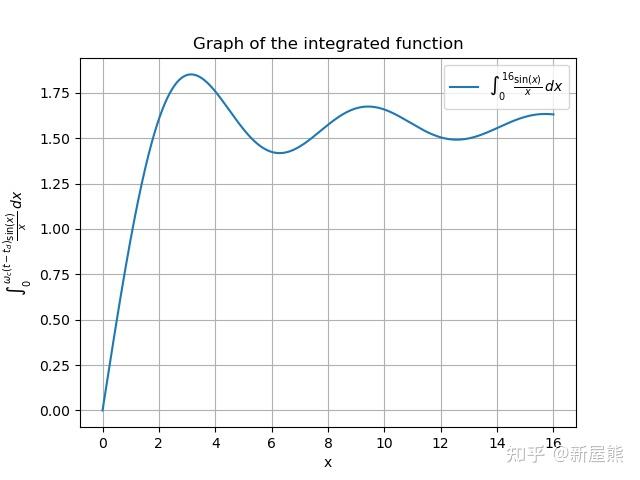 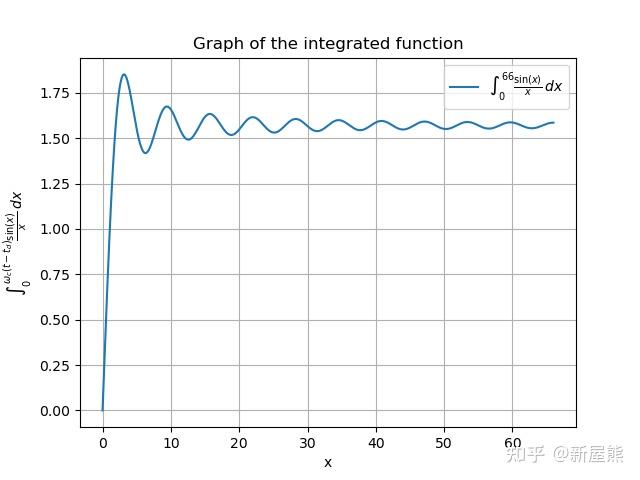 图 6 sin ⁡ x x \\frac {\\sin x}{x} xsinx 的积分区间分别为 (0，16) 与 (0，66) 由图可知， sin ⁡ x x \\frac {\\sin x}{x} xsinx 的积分结果具有明显的威布拉汉姆 - 吉布斯现象特征： x x x 的取值范围越大（对应理想低通滤波器的截止频率 ω c \\omega_c ωc 越高），积分结果震荡的初始幅值上升后，会以较高频率快速衰减。 矩形方波信号可由两个阶跃信号相减得到，因此可证明，方波信号通过理想低通滤波器后的时域波形与公式 (1) 具有相似特征，同样会出现威布拉汉姆 - 吉布斯现象。 #### 3.2 从物理测不准原理分析威布拉汉姆 - 吉布斯现象 威布拉汉姆 - 吉布斯现象亦可通过物理中的测不准原理（又称不确定原理）进行解释。测不准原理指出，粒子位置的不确定性与动量不确定性的乘积不小于普朗克常数（ ℏ \\hbar ℏ）除以 4 π 4\\pi 4π，其数学表达式为： Δ x Δ p ≥ ℏ / 4 π \\Delta x\\Delta p\\ge\\hbar/4\\pi ΔxΔp≥ℏ/4π 对该式进行变换，可得到时间与频率的不确定性关系：时间与频率的乘积不小于 1 / 4 π 1/4\\pi 1/4π，即 Δ t ⋅ Δ f ≥ 1 / 4 π \\Delta t \\cdot \\Delta f\\ge1/4\\pi Δt⋅Δf≥1/4π 该关系表明，对于任意信号，其时间变量 Δ t \\Delta t Δt 与频率变量 Δ f \\Delta f Δf 无法同时无限减小。当二者的乘积达到极限值时，若减小 Δ f \\Delta f Δf，则 Δ t \\Delta t Δt 必然增大。 以理想低通滤波器为例，其理想频谱如图 7 所示，即在无穷小的时间内（ Δ t → 0 \\Delta t \\to 0 Δt→0），信号中高于 ω c \\omega_c ωc 与低于 − ω c -\\omega_c −ωc 的频率分量被完全滤除。但在实际物理场景中，该理想状态无法实现。根据测不准原理，理想滤波器在截止频率 ω c \\omega_c ωc 处的频幅曲线不会出现垂直跳变；结合 Δ t ⋅ Δ ω ≥ 1 2 \\Delta t \\cdot \\Delta \\omega \\geq \\frac{1}{2} Δt⋅Δω≥21（ ω \\omega ω 为角频率），实际理想低通滤波器的频幅曲线会在一小段时间 Δ t \\Delta t Δt 内，频率轴从 ω c \\omega_c ωc 过渡到 ω c + Δ ω \\omega_c + \\Delta \\omega ωc+Δω，幅值轴从 1 衰减至 0，且该衰减过程呈现震荡衰减的特征。从时域角度分析，该震荡的频率随时间动态变化，其范围大致为 ω c \\omega_c ωc 至 ω c + Δ ω \\omega_c + \\Delta \\omega ωc+Δω。 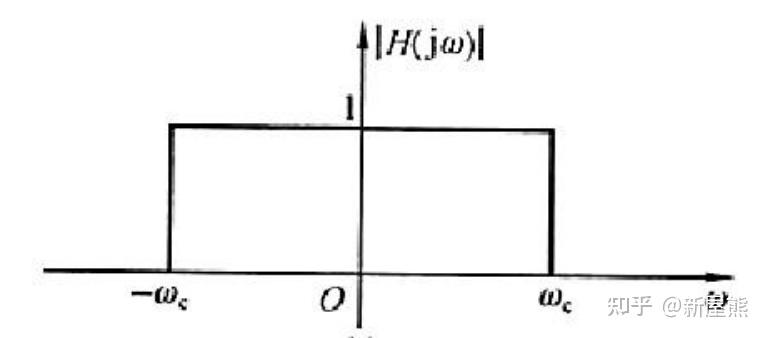 图 7 理想低通滤波器的频谱：在 ω c \\omega_c ωc 和 − ω c -\\omega_c −ωc 处出现频率跳变 ### 4 如何减小或消除威布拉汉姆 - 吉布斯现象 威布拉汉姆 - 吉布斯现象的产生，本质上是傅里叶级数展开过程中选取有限项所导致的。因此，若在信号级数展开时不采用傅里叶级数，而是选用其他信号展开形式（如小波变换），可有效减小甚至消除威布拉汉姆 - 吉布斯现象。 除此之外，减小或消除威布拉汉姆 - 吉布斯现象的方法还包括以下几种（不限于）： **a. 采用窗函数**。信号重建过程中，若使用低通滤波器，易产生威布拉汉姆 - 吉布斯现象。通过在信号中施加适当的窗函数，可减小截断信号带来的振铃效应，常用窗函数包括汉宁窗、汉明窗等。 **b. 过采样** 。若继续选用 sinc \\text {sinc} sinc 低通滤波器，可通过过度采样信号，在重建过程中进行适当滤波，从而减小威布拉汉姆 - 吉布斯现象。 **c. 采用离散余弦变换（DCT）** 。傅里叶级数展开式中同时包含正弦项（ sin ⁡ x \\sin x sinx）与余弦项（ cos ⁡ x \\cos x cosx），其中 sin ⁡ x \\sin x sinx 为奇函数（ sin ⁡ ( x ) = − sin ⁡ ( − x ) \\sin (x)=-\\sin (-x) sin(x)=−sin(−x)）， cos ⁡ x \\cos x cosx 为偶函数（ cos ⁡ ( x ) = cos ⁡ ( − x ) \\cos (x)=\\cos (-x) cos(x)=cos(−x)）。以时间轴为 x x x 轴时， sin ⁡ x \\sin x sinx 不具备时间轴对称性， cos ⁡ x \\cos x cosx 具备时间轴对称性。由于傅里叶级数中存在正弦奇函数项，难以利用函数对称性消除威布拉汉姆 - 吉布斯现象；若构造仅包含余弦项的人工信号，可利用其时间轴对称性消除该现象。 **d. 截断处理**。在信号处理过程中，采用适当的截断技术，可减小边界效应对信号的影响，进而减小威布拉汉姆 - 吉布斯现象。 *** ** * ** *** ## 数学观点下的吉布斯现象 未到江南先一笑 编辑于 2025-02-03 04:53・美国 ### 1 吉布斯现象的数学定义与实例 当采用傅里叶级数表示不连续函数时，傅里叶级数会出现过冲（overshoot）或下冲（undershoot）现象，该现象即为吉布斯现象。以周期为 2 π 2\\pi 2π 的函数 f ( t ) f (t) f(t) 为例，当 t ∈ \[ 0 , 2 π \] t \\in \[0, 2\\pi\] t∈\[0,2π\] 时，其表达式为： f ( t ) = { π 4 , t ∈ \[ 0 , π \] − π 4 , t ∈ ( π , 2 π \] f (t) = \\begin {cases} \\frac {\\pi}{4}, t \\in \[0, \\pi\] \\\\ -\\frac {\\pi}{4}, t \\in (\\pi, 2\\pi\] \\end {cases} f(t)={4π,t∈\[0,π\]−4π,t∈(π,2π

对该函数进行傅里叶级数展开，可得：

f ( t ) = ∑ n = 1 ∞ sin ⁡ ( 2 n − 1 ) t 2 n − 1 f (t) = \sum_{n = 1}^{\infty} \frac {\sin (2n-1) t}{2n-1} f(t)=n=1∑∞2n−1sin(2n−1)t

上式中等号的物理意义为以下极限成立：

lim ⁡ N → ∞ ∫ 0 2 π ∣ f ( t ) − ∑ n = 1 N sin ⁡ ( 2 n − 1 ) t 2 n − 1 ∣ 2 d t = 0 \lim_{N\rightarrow\infty} \int_{0}^{2\pi}\Bigg|f (t) - \sum_{n = 1}^{N} \frac {\sin (2n-1) t}{2n-1} \Bigg|^2 dt = 0 N→∞lim∫02π f(t)−n=1∑N2n−1sin(2n−1)t 2dt=0

即级数 ∑ n = 1 N sin ⁡ ( 2 n − 1 ) t 2 n − 1 \sum_{n = 1}^{N} \frac {\sin (2n-1) t}{2n-1} ∑n=1N2n−1sin(2n−1)t 在范数意义下收敛于 f ( t ) f (t) f(t)，但无法保证该级数一致收敛于 f ( t ) f (t) f(t)。将级数和函数的波形绘制出来，可在函数的间断点（ t = 0 , π t = 0, \pi t=0,π）处清晰观察到吉布斯现象，具体如图所示：

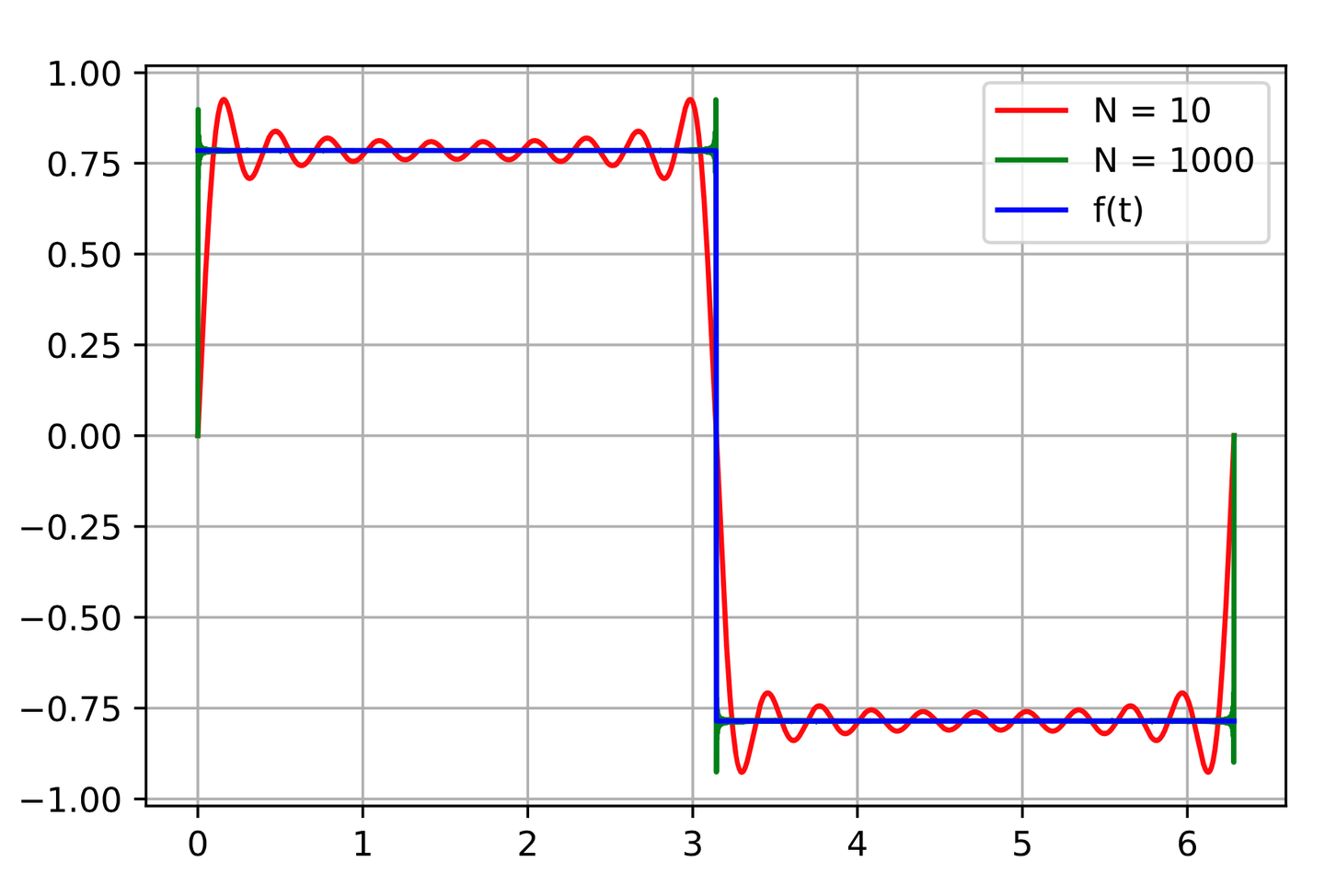
由图可知，有限项傅里叶级数在 t = 0 t = 0 t=0 附近存在过冲，增加 N N N 的取值无法消除该过冲，仅能使过冲点无限趋近于 0。只要函数存在间断点，其傅里叶级数就会出现过冲或下冲现象。

1898 年，迈克尔逊（即通过迈克尔逊 - 莫利实验否定以太漂移的物理学家）发明了一种可计算函数傅里叶级数并通过该级数重建函数的机械设备。他在实验中观察到傅里叶级数在函数间断点处的过冲现象，但当时误认为该现象是由机械设备的精度不足导致的。后续吉布斯通过理论推导证明，该过冲现象的起源是数学本质，而非机械误差。尽管英国数学家 Henry Wilbraham 已于 1848 年从数学层面发现该现象，但由于其论文未受到当时学术界的重视，因此该现象仍被命名为吉布斯现象。

2 过冲现象的数学证明与幅度计算

以下以前文所述函数 f ( t ) f (t) f(t) 为例，证明过冲现象是用解析函数表示不连续函数的必然结果，并给出过冲幅度的具体数值。首先定义有限项傅里叶级数为：

f N ( t ) = ∑ n = 1 N sin ⁡ ( 2 n − 1 ) t 2 n − 1 f_N (t) = \sum_{n = 1}^{N}\frac {\sin (2n-1) t}{2n-1} fN(t)=n=1∑N2n−1sin(2n−1)t

由前文波形图可知，该级数在 t > 0 t > 0 t>0 附近存在一个极大值点。为求解该极大值点的具体数值，对级数求导可得：

f N ′ ( t ) = ∑ n = 1 N cos ⁡ ( 2 n − 1 ) t = Re ( ∑ n = 1 N e i ( 2 n − 1 ) t ) = sin ⁡ ( 2 N t ) 2 sin ⁡ t \begin {align*} f^{\prime}N (t) & = \sum{n = 1}^{N} \cos (2n-1) t \\ &= \text {Re}\Big ( \sum_{n = 1}^{N} e^{i (2n-1) t} \Big) \\ &= \frac {\sin (2Nt) }{2\sin t} \end {align*} fN′(t)=n=1∑Ncos(2n−1)t=Re(n=1∑Nei(2n−1)t)=2sintsin(2Nt)

令 f N ′ ( t ) = 0 f^{\prime}_N (t) = 0 fN′(t)=0，解得极大值点为 t ⋆ = π 2 N t^{\star} = \frac {\pi}{2N} t⋆=2Nπ。将该点代入有限项傅里叶级数，可得其数值为：

f N ( t ⋆ ) = ∑ n = 1 N sin ⁡ ( 2 n − 1 ) π 2 N 2 n − 1 = ∑ n = 1 N sin ⁡ ( 2 n − 1 ) π 2 N ( 2 n − 1 ) π 2 N π 2 N ≈ 1 2 ∫ 0 π sin ⁡ x x d x ≈ 0.925968525991233 \begin {align*} f_N (t^{\star}) & = \sum_{n = 1}^{N}\frac {\sin\frac {(2n-1)\pi}{2N}}{2n-1}\\ &= \sum_{n = 1}^{N}\frac {\sin\frac {(2n-1)\pi}{2N}}{\frac {(2n-1)\pi}{2N}} \frac {\pi}{2N} \\ & \approx \frac {1}{2} \int_{0}^{\pi} \frac {\sin x}{x} dx \\& \approx 0.925968525991233 \end {align*} fN(t⋆)=n=1∑N2n−1sin2N(2n−1)π=n=1∑N2N(2n−1)πsin2N(2n−1)π2Nπ≈21∫0πxsinxdx≈0.925968525991233

显然，该数值大于 π 4 \frac {\pi}{4} 4π。以方波的峰对峰振幅 π 2 \frac {\pi}{2} 2π 为基准，过冲的相对幅度为：

f N ( t ⋆ ) − π 4 π 2 = 1 π ∫ 0 π sin ⁡ x x   d x − 1 2 ≈ 8.9 % \begin{aligned} \frac{f_{N}(t^{\star}) - \frac{\pi}{4}}{\frac{\pi}{2}} &= \frac{1}{\pi}\int_{0}^{\pi}\frac{\sin x}{x}\,\mathrm{d}x - \frac{1}{2} \\ &\approx 8.9\% \end{aligned} 2πfN(t⋆)−4π=π1∫0πxsinxdx−21≈8.9%

该结果具有普适性，适用于任意方波信号。

3 锯齿波的吉布斯现象验证

不连续波形并非仅包含方波，锯齿波也可属于不连续波形。对于锯齿波，其傅里叶级数同样会出现吉布斯现象，且过冲幅度仍为 8.9%。现以周期为 2 的锯齿波函数 g ( t ) g (t) g(t) 为例进行说明，该函数在区间 [ − 1 , 1 ] [-1, 1] [−1,1] 内的表达式为：

g ( t ) = { − π 2 ( t + 1 ) , t ∈ [ − 1 , 0 ] − π 2 ( t − 1 ) , t ∈ ( 0 , 1 ] g (t) = \begin {cases} -\frac {\pi}{2}(t+1), t \in [-1, 0] \\ -\frac {\pi}{2}(t-1), t \in (0, 1] \end {cases} g(t)={−2π(t+1),t∈[−1,0]−2π(t−1),t∈(0,1]

其傅里叶级数展开式为：

g ( t ) = ∑ n = 1 ∞ sin ⁡ n π t n g (t) = \sum_{n = 1}^{\infty} \frac {\sin n\pi t}{n} g(t)=n=1∑∞nsinnπt

该级数同样在范数意义下收敛于 g ( t ) g (t) g(t)，无法保证一致收敛，在函数间断点处仍会出现过冲现象。函数与傅里叶级数的对比波形如图所示：

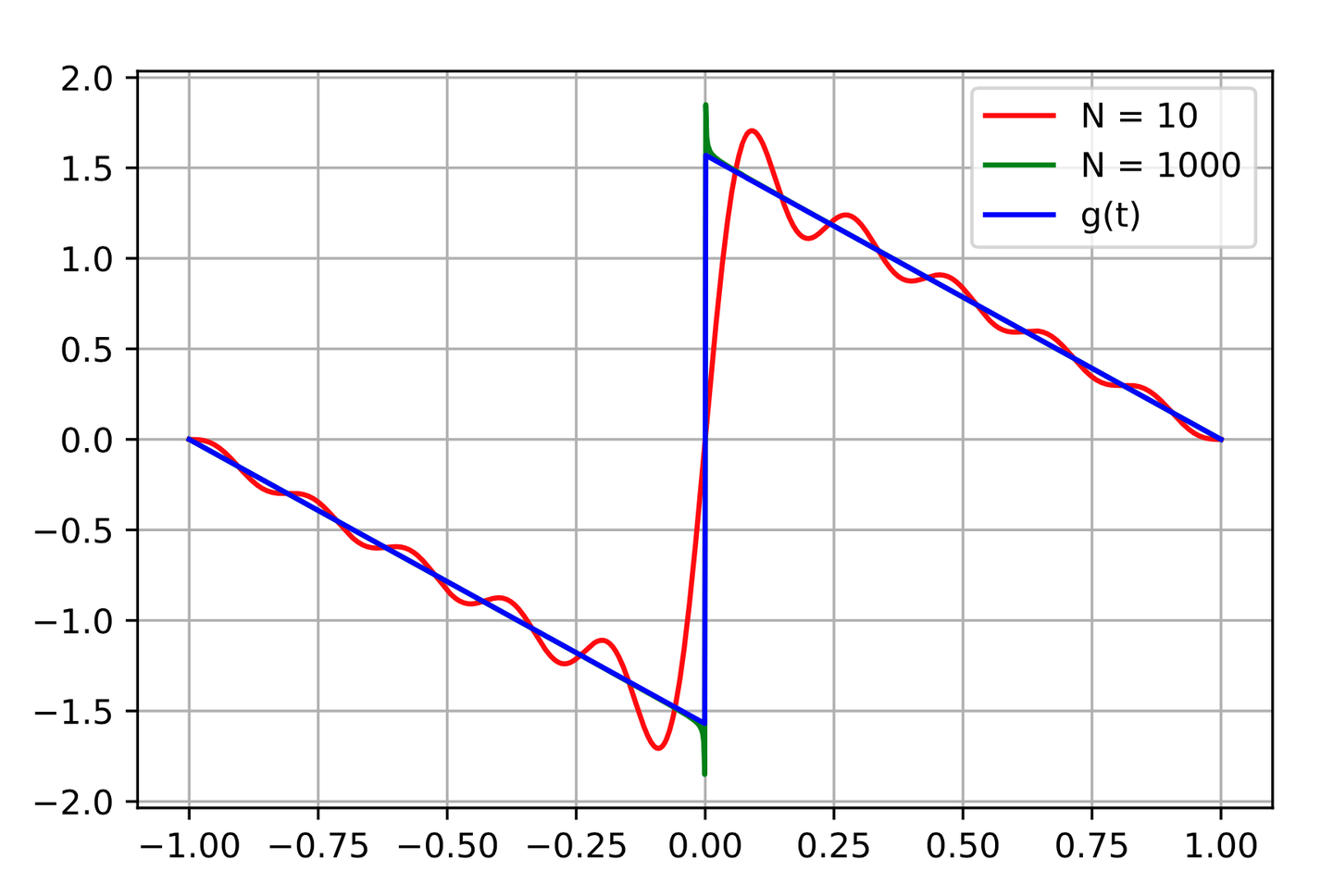
为求解该锯齿波的过冲幅度，定义有限项傅里叶级数为：

g N ( t ) = ∑ n = 1 N sin ⁡ n π t n g_N (t) = \sum_{n = 1}^{N} \frac {\sin n\pi t}{n} gN(t)=n=1∑Nnsinnπt

对其求导可得：

g N ′ ( t ) = π ∑ n = 1 N cos ⁡ n π t = π sin ⁡ ( N + 1 2 ) π t − sin ⁡ π t 2 2 sin ⁡ π t 2 = π cos ⁡ ( N + 1 ) π t 2 sin ⁡ N π t 2 sin ⁡ π t 2 \begin {align*} g^{\prime}N (t) &= \pi \sum{n = 1}^{N} \cos n\pi t \\ &= \pi \frac {\sin\Big (N+\frac {1}{2} \Big) \pi t - \sin\frac {\pi t}{2}}{2\sin\frac {\pi t}{2}} \\ &= \pi \frac {\cos\frac {(N+1)\pi t}{2}\sin\frac {N\pi t}{2}}{\sin\frac {\pi t}{2} } \end {align*} gN′(t)=πn=1∑Ncosnπt=π2sin2πtsin(N+21)πt−sin2πt=πsin2πtcos2(N+1)πtsin2Nπt

令导数为零的最小正数解为 t ⋆ = 1 N + 1 t^{\star} = \frac {1}{N+1} t⋆=N+11，将其代入有限项傅里叶级数，可得级数的最大值为：

g N ( t ⋆ ) = ∑ n = 1 N sin ⁡ n π N + 1 n ≈ ∫ 0 π sin ⁡ x x d x ≈ 1.851937051982466 \begin {align*} g_{N}(t^{\star}) &= \sum_{n = 1}^{N}\frac {\sin\frac {n\pi}{N+1}}{n}\\ &\approx \int_{0}^{\pi} \frac {\sin x}{x} dx \\&\approx 1.851937051982466 \end {align*} gN(t⋆)=n=1∑NnsinN+1nπ≈∫0πxsinxdx≈1.851937051982466

过冲的相对幅度为：

g N ( t ⋆ ) − π 2 π = 1 π ∫ 0 π sin ⁡ x x d x − 1 2 \frac {g_{N}(t^{\star})-\frac {\pi}{2}}{\pi} = \frac {1}{\pi} \int_{0}^{\pi} \frac {\sin x}{x} \mathrm{d}x - \frac {1}{2} πgN(t⋆)−2π=π1∫0πxsinxdx−21

该结果与方波的过冲相对幅度完全一致。

4 连续函数的傅里叶级数收敛特性（无吉布斯现象）

吉布斯现象的本质的是用解析函数拟合不连续函数时产生的固有现象。若函数为连续函数，则不会出现吉布斯现象。以三角波的傅里叶级数展开为例，周期为 2 的三角波函数 Λ ( t ) \Lambda (t) Λ(t) 在区间 [ − 1 , 1 ] [-1, 1] [−1,1] 内的表达式为：

Λ ( t ) = 1 − ∣ t ∣ , t ∈ [ − 1 , 1 ] \Lambda (t) = 1 - |t|, t \in [-1, 1] Λ(t)=1−∣t∣,t∈[−1,1]

该函数在点 − 1 -1 −1、 0 0 0、 1 1 1 处虽不光滑，但均为连续点。其傅里叶级数展开式为：

Λ ( t ) = 1 2 + ∑ n = 1 ∞ 4 ( 2 n − 1 ) 2 π 2 cos ⁡ ( 2 n − 1 ) π t \Lambda (t) = \frac {1}{2} + \sum_{n = 1}^{\infty} \frac {4}{(2n-1)^2 \pi^2 } \cos (2n-1)\pi t Λ(t)=21+n=1∑∞(2n−1)2π24cos(2n−1)πt

该函数的波形如图所示：

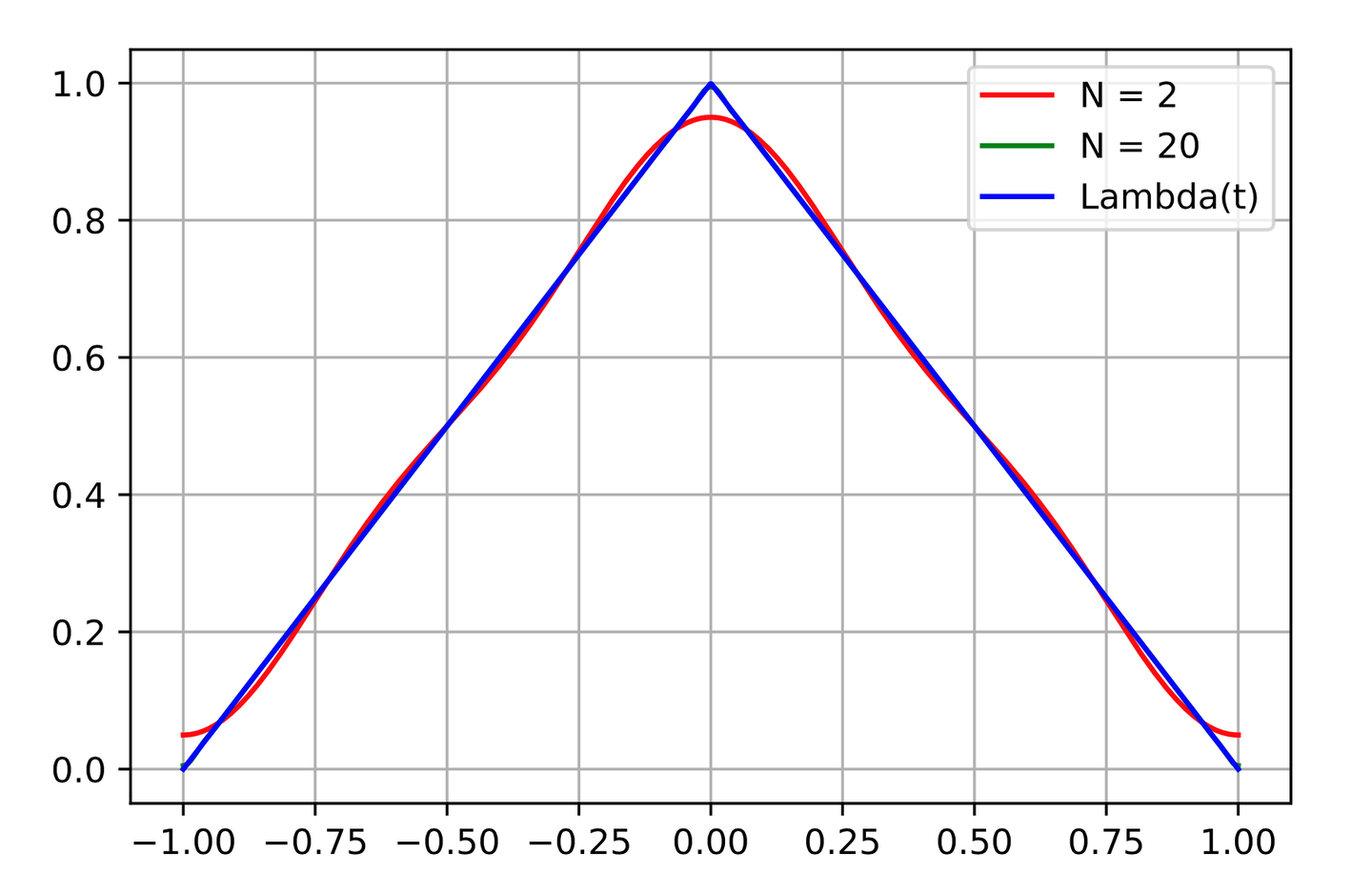
由图可直观观察到，该函数的傅里叶级数收敛速度较快，且在函数不光滑点处未出现过冲或下冲现象，即无吉布斯现象。

5 傅里叶级数收敛速度与吉布斯现象的关联

结合上述三个例子可得出结论：若函数存在不连续性，其傅里叶级数的收敛速度为 1 n \frac {1}{n} n1；若函数为一阶连续函数，其傅里叶级数的收敛速度为 1 n 2 \frac {1}{n^2} n21。

函数的连续程度越高，其傅里叶级数的收敛速度越快。当收敛速度为 1 n \frac {1}{n} n1 时，傅里叶级数虽收敛，但既不绝对收敛，也不一致收敛。

例如级数 ∑ n = 1 ∞ sin ⁡ n π t n \sum_{n=1}^{\infty} \frac {\sin n\pi t}{n} ∑n=1∞nsinnπt，根据狄利克雷判别法可判定其收敛，但不绝对收敛。

图片来源：https://zh.wikipedia.org/wiki/狄利克雷判别法

对于三角波的傅里叶级数

∑ n = 1 ∞ cos ⁡ ( 2 n − 1 ) π t ( 2 n − 1 ) 2 ， \sum_{n = 1}^{\infty} \frac {\cos (2n-1)\pi t }{(2n-1)^2}， n=1∑∞(2n−1)2cos(2n−1)πt，

根据魏尔斯特拉斯 M 判别法（Weierstrass M-test），可判定其绝对收敛且一致收敛。

图片来源：https://en.wikipedia.org/wiki/Weierstrass_M-test

根据魏尔斯特拉斯 M 判别法，满足：

∑ n = 1 ∞ ∣ cos ⁡ ( 2 n − 1 ) π t ( 2 n − 1 ) 2 ∣ ≤ ∑ n = 1 ∞ 1 ( 2 n − 1 ) 2 < ∞ \sum_{n = 1}^{\infty} \Big| \frac {\cos (2n-1)\pi t }{(2n-1)^2} \Big| \le \sum_{n = 1}^{\infty} \frac {1}{(2n-1)^2} < \infty n=1∑∞ (2n−1)2cos(2n−1)πt ≤n=1∑∞(2n−1)21<∞

因此，级数

∑ n = 1 ∞ cos ⁡ ( 2 n − 1 ) π t ( 2 n − 1 ) 2 \sum_{n = 1}^{\infty} \frac {\cos (2n-1)\pi t }{(2n-1)^2} n=1∑∞(2n−1)2cos(2n−1)πt

绝对收敛且一致收敛。

由于该傅里叶级数一致收敛于函数 Λ ( t ) \Lambda (t) Λ(t)，因此不会出现过冲点，即无吉布斯现象。

---

吉布斯现象与振铃效应

1 历史背景与发现

吉布斯现象的研究起源于 19 世纪中叶，该现象历经两次独立发现，且存在长期的命名争议。

历史文献

年份	学者	贡献	文献
1848	Henry Wilbraham	首次观测到傅里叶级数在不连续点附近的振荡特征，完成过冲量的定量估算	On a certain periodic function, Cambridge and Dublin Mathematical Journal, 3: 198--201
1898--1899	J. Willard Gibbs	重新发现并阐释方波傅里叶级数的过冲问题，明确该偏差不会随项数增加趋近于零	Fourier's Series, Nature, 59: 200; 59: 606
1906	Maxime Bôcher	正式定名"吉布斯现象"，完成该现象的首次严格数学证明，构建系统理论框架	Introduction to the theory of Fourier series, Annals of Mathematics, 7: 81--152

历史注记：该现象的首次发现者为 Wilbraham，按学术惯例可命名为"Wilbraham 现象"，受 Gibbs 学术影响力影响，Bôcher 提出的"吉布斯现象"命名得以广泛沿用。1979 年 Hewitt 兄弟发布权威历史综述后，Wilbraham 的首创贡献获得学界普遍认可。

2 数学定义与物理内涵

2.1 基本定义

定义 1.1（吉布斯现象） ：设 f ( x ) f(x) f(x) 为分段光滑函数，在 x 0 x_0 x0 处存在第一类间断点，跳变幅值为 h h h；其傅里叶级数部分和为 S n ( x ) S_n(x) Sn(x)，在 x 0 x_0 x0 邻域内满足：
lim ⁡ n → ∞ max ⁡ x ∈ ( x 0 − δ , x 0 + δ ) ∣ S n ( x ) − f ( x ) ∣ ≈ 0.08949 ⋅ h ≠ 0 \lim_{n\to\infty} \max_{x\in(x_0-\delta,x_0+\delta)} |S_n(x) - f(x)| \approx 0.08949 \cdot h \neq 0 n→∞limx∈(x0−δ,x0+δ)max∣Sn(x)−f(x)∣≈0.08949⋅h=0

即傅里叶级数部分和在不连续点邻域内不具备一致收敛性，产生幅值约为跳变值 8.95% 的固定偏差。

定义 1.2（振铃效应）：信号经过理想低通滤波器或发生频域截断后，时域波形在不连续位置出现的阻尼振荡现象，具体表现为预冲与过冲。

2.2 数学关联

吉布斯现象与振铃效应通过正弦积分函数建立数学关联，正弦积分函数定义为：
S i ( x ) = ∫ 0 x sin ⁡ t t   d t \mathrm{Si}(x) = \int_0^x \frac{\sin t}{t}\,\mathrm{d}t Si(x)=∫0xtsintdt
Wilbraham 常数 （过冲比例系数）：
w = 2 π S i ( π ) − 1 ≈ 0.08949 w = \frac{2}{\pi}\mathrm{Si}(\pi) - 1 \approx 0.08949 w=π2Si(π)−1≈0.08949

术语对照

术语	学科领域	描述重点	数学内涵与物理成因
吉布斯现象	数学分析、调和分析	傅里叶级数的非一致收敛特性	频域截断引发的时域能量泄漏
振铃效应	信号处理、图像处理	时域可观测的振荡波形	吉布斯现象在工程领域的直观体现
过冲/下冲	控制系统、电路理论	波形峰值与理想值的偏差量	定量特征值（≈ 8.95%）

基本结论：振铃效应是吉布斯现象在时域的物理呈现形式，吉布斯现象是振铃效应的数学来源，二者为同一客观现象的不同维度表述。

3 产生条件与机理

吉布斯现象（振铃效应）的产生需同时满足两个必要条件：

1. 频谱锐截止：如理想低通滤波器的矩形频率响应特性；
2. 信号存在跳变：时域信号包含不连续点或边缘特征。

频域-时域对偶关系：

• 频域：信号截断 → 形成有限带宽信号；
• 时域：卷积运算 → 与 sinc 函数的振荡特性耦合。

理想低通滤波器的冲激响应函数：
h ( t ) = ω c π S a [ ω c ( t − t d ) ] , S a ( x ) = sin ⁡ x x h(t) = \frac{\omega_c}{\pi}\mathrm{Sa}\left[\omega_c(t-t_{\mathrm{d}})\right], \quad \mathrm{Sa}(x) = \frac{\sin x}{x} h(t)=πωcSa[ωc(t−td)],Sa(x)=xsinx

sinc 函数（ S a \mathrm{Sa} Sa 函数）的固有振荡特性，是时域振铃效应产生的直接原因。

4 学科归属：连续与离散

4.1 理论源头

吉布斯现象起源于连续时间信号与系统理论，属于数学分析的经典研究结果，并非数字信号处理（DSP）的专属概念。

学科归属

维度	吉布斯现象	振铃效应
起源领域	数学分析、傅里叶级数理论（连续时间）	数字信号处理、图像处理（离散时间）
理论内涵	连续傅里叶级数的非一致收敛特性	离散傅里叶变换（DFT）频域截断的时域结果
数学基础	黎曼积分、正弦积分 S i ( x ) \mathrm{Si}(x) Si(x)	离散卷积、循环卷积、有限长序列分析
历史文献	Wilbraham (1848)、Gibbs (1899)、Bôcher (1906)	现代数字信号处理教材（Oppenheim、Proakis 等）

4.2 在数字信号处理中的体现

数字信号处理中，吉布斯现象通过以下机制实现：

（1）离散傅里叶变换（DFT）的频域截断

对无限长序列 x [ n ] x[n] x[n] 进行 N N N 点截断，等效为序列与矩形窗 w [ n ] w[n] w[n] 相乘：
x N [ n ] = x [ n ] ⋅ w [ n ] , w [ n ] = { 1 , 0 ≤ n ≤ N − 1 0 , 其他 x_N[n] = x[n] \cdot w[n], \quad w[n] = \begin{cases} 1, & 0 \leq n \leq N-1 \\ 0, & \text{其他} \end{cases} xN[n]=x[n]⋅w[n],w[n]={1,0,0≤n≤N−1其他

频域等效为循环卷积 运算：
X N ( e j ω ) = 1 2 π X ( e j ω ) ⊛ W ( e j ω ) X_N(e^{j\omega}) = \frac{1}{2\pi} X(e^{j\omega}) \circledast W(e^{j\omega}) XN(ejω)=2π1X(ejω)⊛W(ejω)

其中 W ( e j ω ) = sin ⁡ ( N ω / 2 ) sin ⁡ ( ω / 2 ) e − j ( N − 1 ) ω / 2 W(e^{j\omega}) = \frac{\sin(N\omega/2)}{\sin(\omega/2)}e^{-j(N-1)\omega/2} W(ejω)=sin(ω/2)sin(Nω/2)e−j(N−1)ω/2 为 Dirichlet 核（离散时间 sinc 函数），其振荡特性会引发频谱泄漏与时域振铃。

（2）FIR 滤波器设计

采用窗函数法 设计 FIR 滤波器时，理想无限长冲激响应 h d [ n ] h_d[n] hd[n] 被截断为有限长序列：
h [ n ] = h d [ n ] ⋅ w [ n ] , n = 0 , 1 , ... , N − 1 h[n] = h_d[n] \cdot w[n], \quad n = 0, 1, \dots, N-1 h[n]=hd[n]⋅w[n],n=0,1,...,N−1

若选取矩形窗，频率响应 H ( e j ω ) H(e^{j\omega}) H(ejω) 在通带边缘会出现吉布斯振荡，具体表现为：

• 通带波纹；
• 阻带波纹；
• 过渡带过冲与下冲。

窗函数对吉布斯现象的影响

窗函数类型	主瓣宽度	旁瓣衰减	吉布斯过冲
矩形窗	4 π / N 4\pi/N 4π/N	− 13 -13 −13 dB	8.95%（最大值）
Hanning 窗	8 π / N 8\pi/N 8π/N	− 31 -31 −31 dB	显著降低
Hamming 窗	8 π / N 8\pi/N 8π/N	− 41 -41 −41 dB	优化抑制
Blackman 窗	12 π / N 12\pi/N 12π/N	− 57 -57 −57 dB	进一步降低

5 经典文献与权威综述

5.1 必读基础文献

[1] Hewitt, E. & Hewitt, R.E. (1979) --- 历史溯源权威文献

The Gibbs-Wilbraham phenomenon: An episode in Fourier analysis , Archive for History of Exact Sciences, 21(2): 129--160

文献价值：厘清 Wilbraham 与 Gibbs 的学术贡献，纠正命名偏差

[2] Bôcher, M. (1906) --- 数学理论奠基文献

Introduction to the theory of Fourier series , Annals of Mathematics, 7: 81--152

文献价值：完成吉布斯现象的首次严格数学证明，确立术语定名

[3] Thompson, W.J. (1992) --- 教学阐释经典文献

Fourier series and the Gibbs phenomenon , American Journal of Physics, 60(5): 425--429

文献价值：从物理教学视角，直观阐释现象产生机理

5.2 现代扩展与应用

[4] Jerri, A.J. (1998)

The Gibbs Phenomenon in Fourier Analysis, Splines and Wavelet Approximations , Springer

文献价值：覆盖小波分析、样条逼近等现代逼近方法中的吉布斯现象

[5] Gottlieb, D. & Shu, C.-W. (1997)

On the Gibbs phenomenon and its resolution , SIAM Review, 39(4): 644--668

文献价值：吉布斯现象消除方法的开创性综述

[6] 医学成像应用

磁共振成像（MRI）中，吉布斯振铃伪影是频域截断引发的典型伪影，表现为组织边缘的明暗交替条纹。

5.3 经典教材

教材	作者	章节定位	表述方式
Signals and Systems (2nd Ed.)	Oppenheim, Willsky, Nawab	第 4 章（连续时间傅里叶级数）	作为连续时间傅里叶级数的收敛特性阐释
Discrete-Time Signal Processing (3rd Ed.)	Oppenheim, Schafer	第 7 章（FIR 滤波器设计）	窗函数法中的吉布斯现象分析
Digital Signal Processing (4th Ed.)	Proakis, Manolakis	第 10 章（滤波器设计）	频域截断引发的振铃效应
The Fourier Transform and Its Applications	Bracewell	第 6 章	连续与离散信号框架下的统一阐释

6 抑制与消除方法

常用抑制策略

方法	原理	效果	代价
频域加窗	以 Hanning、Hamming 等非矩形窗替代矩形窗	降低旁瓣幅值，减弱振铃效应	主瓣宽度增加，信号分辨率降低
时域加窗	对截断信号施加平滑窗函数	抑制信号边缘不连续引发的振荡	引入信号幅度偏差
自适应滤波	依据信号局部特征调整滤波器参数	保留信号边缘，抑制振铃	计算复杂度提升
Gegenbauer 重构	基于正交多项式的信号后处理	实现指数收敛，消除吉布斯现象	需预先确定信号跳变位置

7 本章小结

1. 历史定名：1848 年由 Wilbraham 首次发现，1899 年 Gibbs 重新发现，1906 年 Bôcher 完成严格证明并定名。
2. 概念关系：吉布斯现象为傅里叶分析层面的数学来源，振铃效应为信号处理层面的物理呈现，二者为同一现象的不同表述。
3. 定量特征：过冲幅值为跳变值的 8.95%（Wilbraham 常数），该数值与截断频率无关。
4. 产生条件：频谱锐截止与信号不连续同时存在，为现象产生的充要条件。
5. 学科归属 ：吉布斯现象起源于连续时间 数学分析，在数字信号处理中以振铃效应形式呈现，是跨越连续与离散、数学与工程的基础概念。
6. 工程价值：在 FIR 滤波器设计、图像处理（JPEG、MRI）、频谱分析、数值计算等领域具备广泛实践应用价值。

参考文献

1\] Wilbraham H. On a certain periodic function\[J\]. Cambridge and Dublin Mathematical Journal, 1848, 3: 198-201. \[2\] Gibbs J W. Fourier's Series\[J\]. Nature, 1898-1899, 59: 200, 606. \[3\] Bôcher M. Introduction to the theory of Fourier series\[J\]. Annals of Mathematics, 1906, 7: 81-152. \[4\] Hewitt E, Hewitt R E. The Gibbs-Wilbraham phenomenon: An episode in Fourier analysis\[J\]. Archive for History of Exact Sciences, 1979, 21(2): 129-160. \[5\] Thompson W J. Fourier series and the Gibbs phenomenon\[J\]. American Journal of Physics, 1992, 60(5): 425-429. \[6\] Jerri A J. The Gibbs Phenomenon in Fourier Analysis, Splines and Wavelet Approximations\[M\]. Berlin: Springer, 1998. \[7\] Gottlieb D, Shu C W. On the Gibbs phenomenon and its resolution\[J\]. SIAM Review, 1997, 39(4): 644-668. \[8\] Oppenheim A V, Willsky A S, Nawab S H. Signals and Systems\[M\]. 2nd ed. Upper Saddle River: Prentice Hall, 1997. \[9\] Oppenheim A V, Schafer R W. Discrete-Time Signal Processing\[M\]. 3rd ed. Upper Saddle River: Prentice Hall, 2010. \[10\] Proakis J G, Manolakis D G. Digital Signal Processing\[M\]. 4th ed. Boston: Pearson, 2007. *** ** * ** *** ## reference： * 什么是吉布斯现象 - CSDN 博客 * 吉布斯效应 (Gibbs)、振铃 (ring) 现象和块效应 (Blocking Artifac)-CSDN 博客 * 吉布斯现象产生的原因 --- 兼论谁先发现吉布斯现象的？ - 知乎 * 数学观点下的吉布斯现象 - 知乎 * ......