探索人工势场法：简单高效的路径规划算法

人工势场法路径规划算法势函数法 APF 简单，高效

在路径规划领域，人工势场法（Artificial Potential Field，APF）可是个相当有趣且实用的算法。它简单又高效，为解决机器人等设备的路径规划问题提供了一种独特的思路。

势函数法 APF 简介

人工势场法的核心思想是通过构建虚拟的势场来引导物体从起点移动到终点。它定义了两种势场：引力场和斥力场。引力场引导物体趋向目标点，就好像有一股无形的力量在拉着它；斥力场则避免物体与障碍物碰撞，当物体靠近障碍物时，斥力会迅速增大，将物体推开。

我们可以用一个简单的公式来表示势函数：

\[ U(q) = U*{att}(q) + U*{rep}(q) \]

其中，\( U(q) \) 是总的势函数，\( U*{att}(q) \) 是引力势函数，\( U*{rep}(q) \) 是斥力势函数。

引力势函数通常可以表示为：

\[ U*{att}(q) = - \frac{1}{2} k*{att} || q - q_{goal} ||^2 \]

这里，\( k*{att} \) 是引力系数，\( q \) 是物体当前位置，\( q*{goal} \) 是目标位置。这个公式的意思很直观，距离目标点越近，引力势能越小，就像被目标点吸引得越厉害。

人工势场法路径规划算法势函数法 APF 简单，高效

斥力势函数则相对复杂一些：

\[ U*{rep}(q) = \sum*{i=1}^{n} \begin{cases}

\frac{1}{2} k*{rep} (\frac{1}{d* {i}} - \frac{1}{d*{0}})^2, & \text{if } d*{i} \lt d_{0} \\

0, & \text{otherwise}

\end{cases} \]

其中，\( k*{rep} \) 是斥力系数，\( d* {i} = || q - q*{obs* i} || \) 表示物体到第 \( i \) 个障碍物的距离，\( d*{0} \) 是一个设定的距离阈值。当物体距离障碍物小于 \( d*{0} \) 时，斥力势能迅速增大，起到排斥作用，防止碰撞。

简单示例代码

下面我们用 Python 来简单实现一下人工势场法的路径规划。

python 复制代码

import numpy as np
import matplotlib.pyplot as plt


# 引力势函数
def attractive_potential(current, goal, k_att):
    return -0.5 * k_att * np.linalg.norm(current - goal) ** 2


# 斥力势函数
def repulsive_potential(current, obstacles, k_rep, d0):
    rep_pot = 0
    for obs in obstacles:
        dist = np.linalg.norm(current - obs)
        if dist < d0:
            rep_pot += 0.5 * k_rep * (1 / dist - 1 / d0) ** 2
    return rep_pot


# 计算合力
def compute_force(current, goal, obstacles, k_att, k_rep, d0):
    att_force = -attractive_potential(current, goal, k_att) * (current - goal) / np.linalg.norm(current - goal)
    rep_force = np.zeros_like(current)
    for obs in obstacles:
        dist = current - obs
        if np.linalg.norm(dist) < d0:
            rep_force += -repulsive_potential(current, [obs], k_rep, d0) * dist / np.linalg.norm(dist)
    total_force = att_force + rep_force
    return total_force


# 模拟路径规划
def simulate_path(start, goal, obstacles, k_att=1, k_rep=10, d0=5, step_size=0.1, max_iter=1000):
    current = start
    path = [current]
    for _ in range(max_iter):
        force = compute_force(current, goal, obstacles, k_att, k_rep, d0)
        new_position = current + step_size * force / np.linalg.norm(force)
        if np.linalg.norm(new_position - goal) < step_size:
            path.append(goal)
            break
        current = new_position
        path.append(current)
    return np.array(path)


# 示例参数
start = np.array([0, 0])
goal = np.array([10, 10])
obstacles = [np.array([5, 5])]

# 运行模拟
path = simulate_path(start, goal, obstacles)

# 绘制结果
plt.plot(path[:, 0], path[:, 1], '-o')
plt.scatter(start[0], start[1], c='r', label='Start')
plt.scatter(goal[0], goal[1], c='g', label='Goal')
for obs in obstacles:
    plt.scatter(obs[0], obs[1], c='b', label='Obstacle')
plt.legend()
plt.title('Path Planning with APF')
plt.xlabel('X')
plt.ylabel('Y')
plt.grid(True)
plt.show()

代码分析

这段代码实现了一个基本的人工势场法路径规划。

引力势函数 attractivepotential *：
- 计算当前位置与目标位置之间的引力势能。
- 公式 return -0.5 katt * np.linalg.norm(current - goal) `` 2 清晰地体现了引力与距离目标点的关系，距离越近，引力势能越小。

斥力势函数 repulsivepotential *：
- 遍历所有障碍物，计算物体到每个障碍物的距离。
- 如果距离小于设定阈值 d0，则根据公式计算该障碍物产生的斥力势能并累加。
- 这里的公式 rep* pot += 0.5 k_rep (1 / dist - 1 / d0) `` 2 保证了距离障碍物越近，斥力势能增长得越快。

计算合力 computeforce *：
- 首先计算引力产生的力，通过 -attractive* potential(current, goal, k_att) * (current - goal) / np.linalg.norm(current - goal) 得到引力方向上的力。
- 然后遍历障碍物，计算每个障碍物产生的斥力并累加。
- 最终返回合力，这个合力将引导物体在势场中移动。

模拟路径规划 simulatepath *：
- 初始化当前位置为起点，将起点加入路径列表。
- 在循环中，根据合力更新当前位置，步长为 step* size。
- 如果新位置接近目标点，则将目标点加入路径并结束循环。
- 每次更新位置后，将新位置加入路径列表，最终返回整个路径。

主程序部分 ：
- 定义了起点、目标点和障碍物的位置。
- 调用 simulate_path 函数进行路径规划。
- 最后使用 matplotlib 绘制路径、起点、目标点和障碍物，直观展示路径规划的结果。

人工势场法真的是一种简单又高效的路径规划算法，通过这个示例代码，我们可以更清楚地看到它的工作原理和实现方式。希望大家对这个有趣的算法有了更深入的了解！

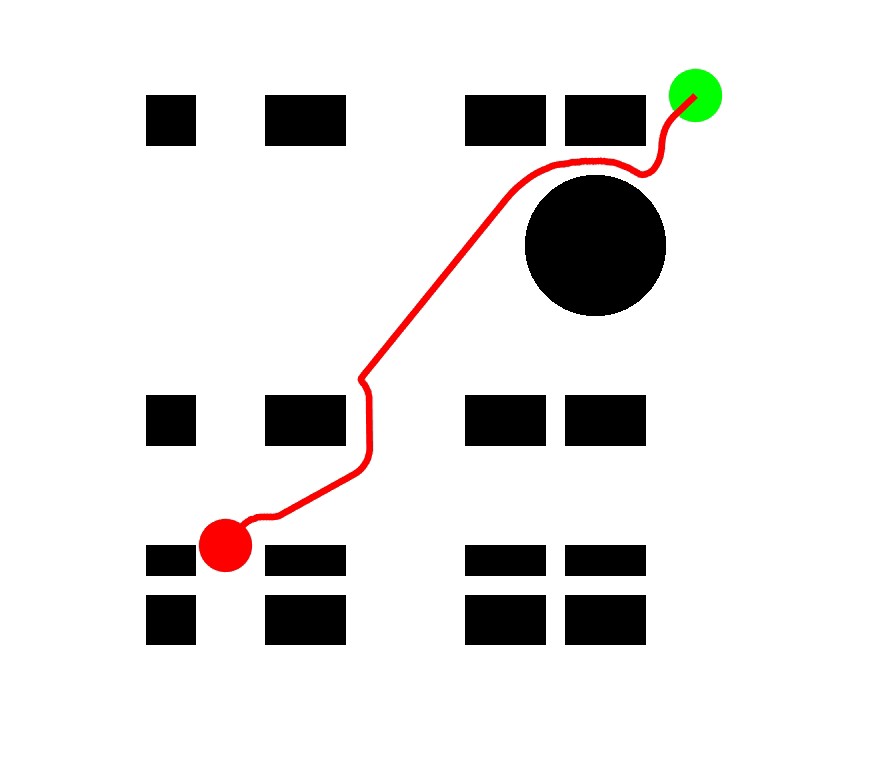
以上就是关于人工势场法路径规划算法的一篇博文啦，代码和分析都在这儿，是不是感觉挺有意思的😃

你可以根据实际情况调整代码中的参数，看看不同参数设置下路径规划的效果会有什么变化哦🧐。