探索一维声子晶体结构带隙仿真模型

一维声子晶体结构带隙仿真模型

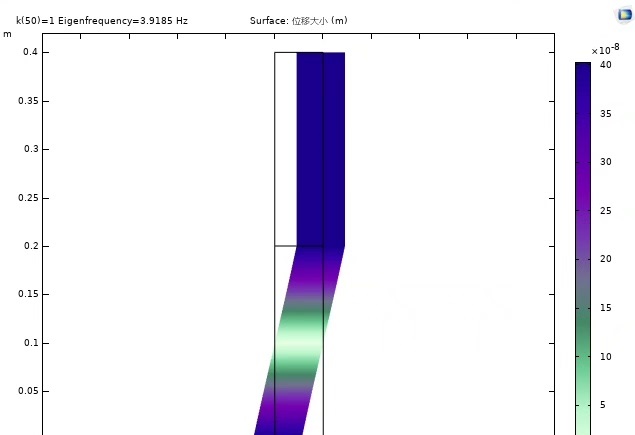
在材料科学与物理学的交叉领域，声子晶体是一个极具吸引力的研究对象。今天咱们就来深入聊聊一维声子晶体结构带隙的仿真模型。

什么是一维声子晶体

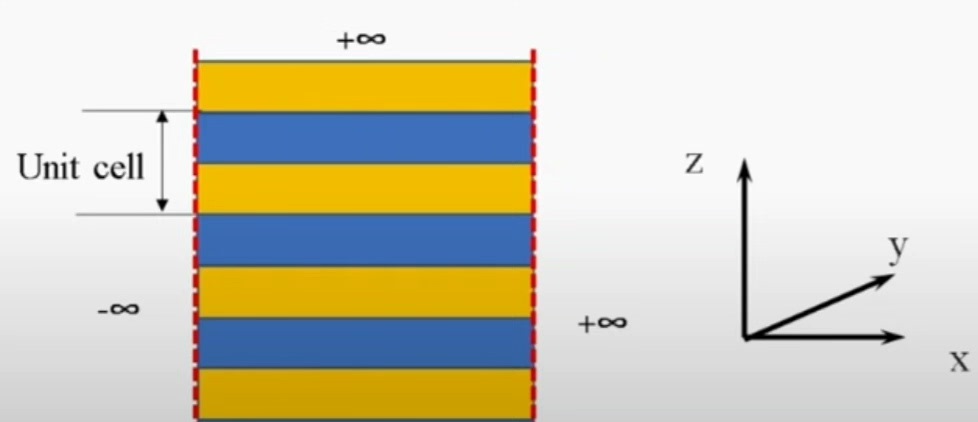
简单来说，声子晶体是一种具有周期性结构的人工复合材料，其声学特性就像半导体晶体对电子的作用一样，能够对弹性波或声波产生特殊的影响。一维声子晶体则是在一个方向上具有周期性结构的声子晶体。

带隙的奥秘

带隙是声子晶体的核心特性之一。在某些频率范围内，弹性波或声波无法在声子晶体中传播，这个频率范围就被称为带隙。就好比给特定频率的声波竖起了一道"高墙"，禁止通行。带隙的存在使得声子晶体在隔音、滤波等众多领域有着巨大的应用潜力。

仿真模型搭建

理论基础

要构建仿真模型，我们得从理论出发。对于一维声子晶体，常用的理论模型是平面波展开法。这个方法基于晶体的周期性结构，将波动方程中的位移场用平面波的线性组合来表示。以一维弹性波在声子晶体中的传播为例，假设声子晶体由两种材料交替排列组成，其波动方程可写为：

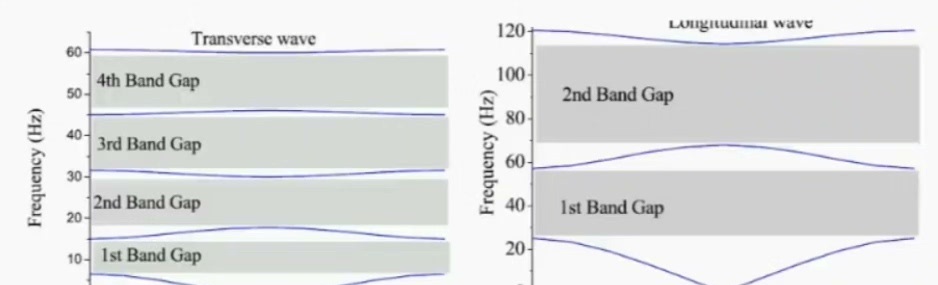
一维声子晶体结构带隙仿真模型

\[ \rho(x)\frac{\partial^{2}u(x,t)}{\partial t^{2}} = \frac{\partial}{\partial x}\left[Y(x)\frac{\partial u(x,t)}{\partial x}\right] \]

其中，\(\rho(x)\) 是材料密度，\(Y(x)\) 是杨氏模量，\(u(x,t)\) 是位移场。由于结构的周期性，\(\rho(x)\) 和 \(Y(x)\) 都是周期函数。

代码实现（以Python为例）

下面咱们看一段简单的Python代码示例，用有限元方法来初步模拟一维声子晶体的带隙。

python 复制代码

import numpy as np
import matplotlib.pyplot as plt


# 定义材料参数
rho1 = 1000  # 材料1密度
rho2 = 2000  # 材料2密度
Y1 = 1e9  # 材料1杨氏模量
Y2 = 2e9  # 材料2杨氏模量
a = 0.1  # 晶格常数
N = 20  # 周期数

# 构建质量矩阵和刚度矩阵
M = np.zeros((2 * N, 2 * N))
K = np.zeros((2 * N, 2 * N))

for i in range(N):
    if i % 2 == 0:
        rho = rho1
        Y = Y1
    else:
        rho = rho2
        Y = Y2
    M[2 * i, 2 * i] += rho * a / 2
    M[2 * i + 1, 2 * i + 1] += rho * a / 2
    M[2 * i, 2 * i + 1] += rho * a / 4
    M[2 * i + 1, 2 * i] += rho * a / 4

    K[2 * i, 2 * i] += Y / a
    K[2 * i + 1, 2 * i + 1] += Y / a
    K[2 * i, 2 * i + 1] -= Y / a
    K[2 * i + 1, 2 * i] -= Y / a

    if i < N - 1:
        if (i + 1) % 2 == 0:
            rho_next = rho1
            Y_next = Y1
        else:
            rho_next = rho2
            Y_next = Y2
        M[2 * i + 1, 2 * i + 2] += rho * a / 4
        M[2 * i + 2, 2 * i + 1] += rho * a / 4
        M[2 * i + 2, 2 * i + 2] += rho_next * a / 2
        K[2 * i + 1, 2 * i + 2] -= Y / a
        K[2 * i + 2, 2 * i + 1] -= Y_next / a


# 求解特征值问题
eigenvalues, eigenvectors = np.linalg.eigh(K, M)
frequencies = np.sqrt(eigenvalues) / (2 * np.pi)


# 绘制能带图
plt.plot(frequencies)
plt.xlabel('Band Index')
plt.ylabel('Frequency (Hz)')
plt.title('One - Dimensional Phononic Crystal Band Structure')
plt.grid(True)
plt.show()

代码分析

材料参数定义：首先我们设定了两种材料的密度（\(\rho1\)，\(\rho2\)）和杨氏模量（\(Y1\)，\(Y2\)），还有晶格常数 \(a\) 和周期数 \(N\)。这些参数是决定声子晶体特性的关键因素。
矩阵构建：质量矩阵 \(M\) 和刚度矩阵 \(K\) 是有限元方法的核心。通过循环遍历每个周期，根据当前周期所处的材料，给矩阵元素赋值。例如，质量矩阵中，对于每个节点，会根据材料密度和晶格常数来确定其对应的质量贡献；刚度矩阵则根据材料的杨氏模量和晶格常数来确定节点间的刚度联系。
特征值求解 ：利用 np.linalg.eigh 函数求解广义特征值问题，得到特征值和特征向量。这里的特征值经过处理后就对应着不同的振动频率。
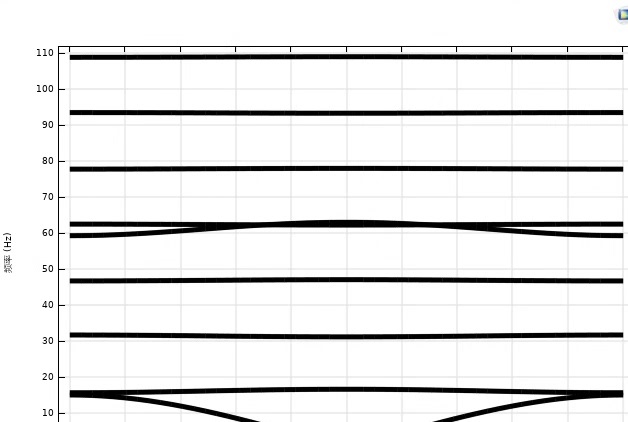
绘图展示 ：最后用 matplotlib 库将频率绘制出来，得到能带图，从图中我们就能直观地看到带隙的大致位置。

总结

通过上述理论和代码示例，我们初步搭建了一维声子晶体结构带隙的仿真模型。当然，实际研究中还需要考虑更多因素，如边界条件的精确处理、不同材料的复杂特性等，但这个简单模型为我们打开了探索声子晶体带隙特性的大门，希望大家能从中获得启发，进一步深入研究这个有趣的领域。