基于TOA/FOA的无源定位方法MATLAB仿真探索

MATLAB仿真基于toa/foa的无源定位方法，二次等式约束求解有参考文档无源定位技术：二次等式约束最小二乘估计理论与方法第八章

在无线定位领域，基于TOA（Time of Arrival，到达时间）和FOA（Frequency of Arrival，到达频率）的无源定位方法一直备受关注。这种方法无需目标主动发射信号，通过接收目标反射或辐射的信号来确定其位置，在军事侦察、智能交通等诸多场景有着重要应用。而二次等式约束求解则是实现精确无源定位的关键环节。本文将结合《二次等式约束最小二乘估计理论与方法》第八章的参考文档，深入探讨并通过MATLAB进行仿真实现。

TOA/FOA原理简述

TOA利用信号从发射源到各个接收站的传播时间差来确定目标位置。假设已知信号传播速度 \( c \)，通过测量信号到达不同接收站的时间 \( t_i \)，可以建立关于目标位置 \( (x, y) \) 的方程：

\[ \sqrt{(x - xi)^2 + (y - yi)^2} = c \cdot t_i \]

其中 \( (xi, yi) \) 是第 \( i \) 个接收站的坐标。

FOA则是基于信号到达不同接收站的频率差异，利用多普勒效应原理来辅助定位。当目标与接收站存在相对运动时，接收站接收到的信号频率会发生变化。通过测量这些频率变化，可以进一步约束目标的位置信息。

二次等式约束最小二乘估计

在实际情况中，由于测量误差等因素，上述基于TOA和FOA建立的方程往往存在噪声干扰。为了得到更准确的目标位置估计，二次等式约束最小二乘估计方法应运而生。其核心思想是在满足一定二次等式约束条件下，最小化观测值与估计值之间的误差平方和。

MATLAB仿真基于toa/foa的无源定位方法，二次等式约束求解有参考文档无源定位技术：二次等式约束最小二乘估计理论与方法第八章

假设我们有 \( n \) 个接收站，观测向量 \( \mathbf{z} \) 包含了TOA和FOA等测量信息，估计向量 \( \mathbf{\hat{x}} \) 为目标位置的估计值。目标函数可以表示为：

\[ J(\mathbf{\hat{x}}) = (\mathbf{z} - h(\mathbf{\hat{x}}))^T (\mathbf{z} - h(\mathbf{\hat{x}})) \]

其中 \( h(\mathbf{\hat{x}}) \) 是关于估计值 \( \mathbf{\hat{x}} \) 的非线性函数，它根据TOA和FOA的测量模型得到。同时，存在二次等式约束条件 \( g(\mathbf{\hat{x}}) = 0 \)。通过拉格朗日乘数法，将约束问题转化为无约束优化问题进行求解。

MATLAB仿真实现

matlab 复制代码

% 1. 参数设置
c = 3e8; % 信号传播速度
num_stations = 4; % 接收站数量
stations = [0 0; 100 0; 0 100; 100 100]; % 接收站坐标

% 2. 生成模拟目标位置和测量噪声
true_position = [50 50]; % 真实目标位置
toa_noise = 1e-8; % TOA测量噪声标准差
foa_noise = 100; % FOA测量噪声标准差

% 3. 计算真实TOA和FOA
true_toa = zeros(num_stations, 1);
true_foa = zeros(num_stations, 1);
for i = 1:num_stations
    distance = norm(true_position - stations(i, :));
    true_toa(i) = distance / c;
    % 简单模拟FOA，假设目标相对接收站有一定速度
    relative_velocity = [100 100]; % 相对速度向量
    true_foa(i) = (c / distance) * relative_velocity * (true_position - stations(i, :))';
end

% 4. 添加噪声
measured_toa = true_toa + toa_noise * randn(num_stations, 1);
measured_foa = true_foa + foa_noise * randn(num_stations, 1);

% 5. 二次等式约束最小二乘求解
% 这里简单使用fsolve函数来求解非线性最小二乘问题，实际中可能需要更复杂的方法
fun = @(position) [sqrt((position(1) - stations(:, 1)).^2 + (position(2) - stations(:, 2)).^2) / c - measured_toa;
                   % 这里简单添加一个关于FOA的等式约束示例，实际需更准确模型
                   (c./ sqrt((position(1) - stations(:, 1)).^2 + (position(2) - stations(:, 2)).^2)) * [100 100] * (position - stations(:, :))' - measured_foa];
initial_guess = [0 0];
estimated_position = fsolve(fun, initial_guess);

代码分析

参数设置部分 ：定义了信号传播速度 c，接收站数量 num_stations 以及接收站的坐标 stations。这些参数是后续计算的基础，不同的场景和应用可能需要调整这些参数。
生成模拟目标位置和测量噪声 ：设置了真实目标位置 trueposition*，并定义了TOA和FOA测量噪声的标准差 toa* noise 和 foa_noise。噪声的引入模拟了实际测量中的不确定性，对定位精度有着重要影响。
计算真实TOA和FOA：通过计算目标到每个接收站的距离，根据TOA和FOA的原理得到真实的TOA和FOA值。这里对于FOA的计算做了简单模拟，实际应用中需要更精确的基于多普勒效应的模型。
添加噪声 ：使用 randn 函数为真实的TOA和FOA测量值添加高斯白噪声，模拟实际测量情况。噪声的存在使得定位问题更具挑战性，也凸显了二次等式约束最小二乘估计方法的重要性。
二次等式约束最小二乘求解 ：定义了一个匿名函数 fun，该函数包含了基于TOA和FOA测量模型的等式约束。然后使用 fsolve 函数来求解这个非线性最小二乘问题，fsolve 会迭代寻找使 fun 函数值接近零的估计位置 estimated_position。在实际应用中，可能需要根据具体问题调整求解器或采用更复杂的优化算法来提高求解的准确性和效率。

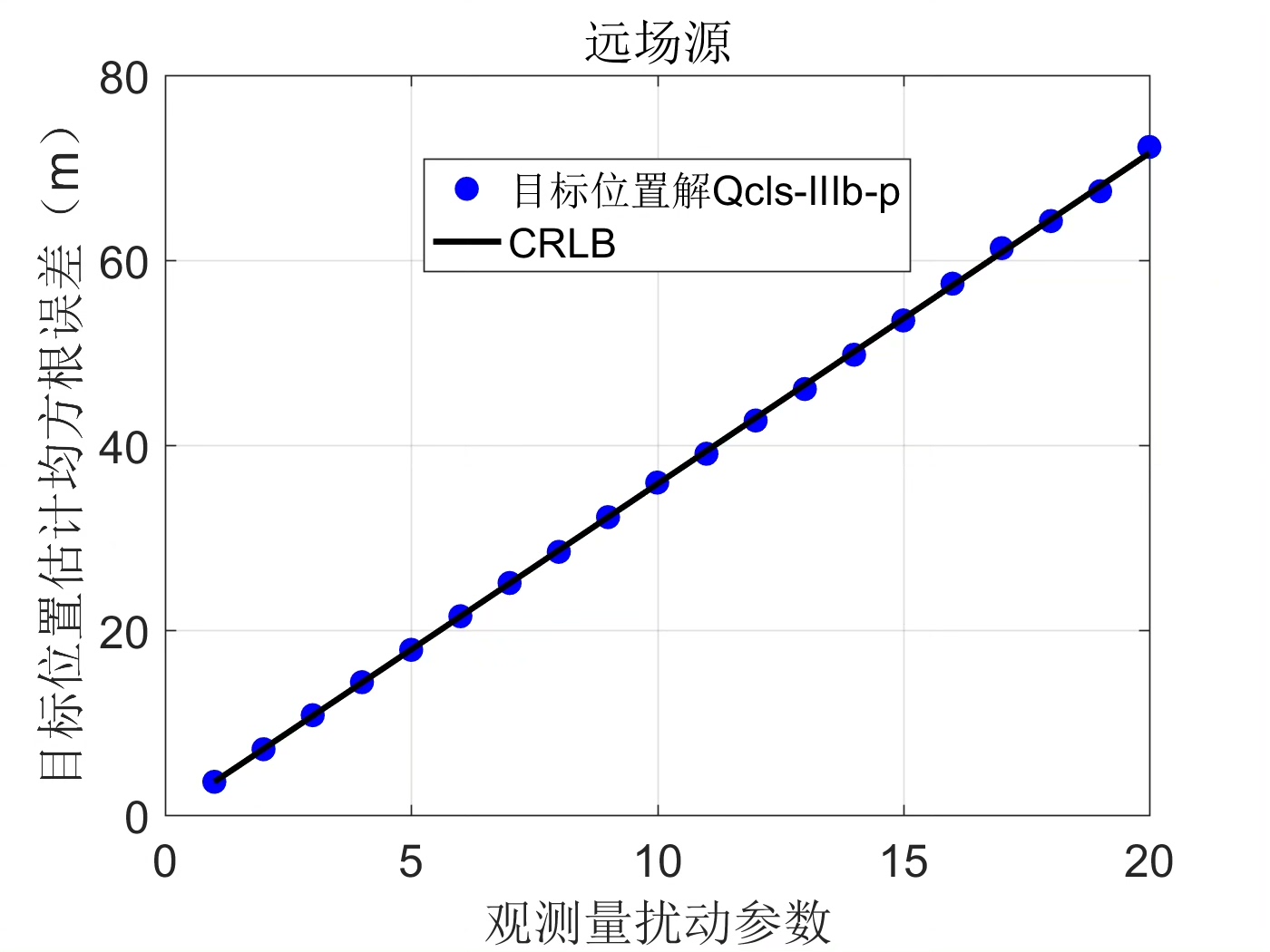
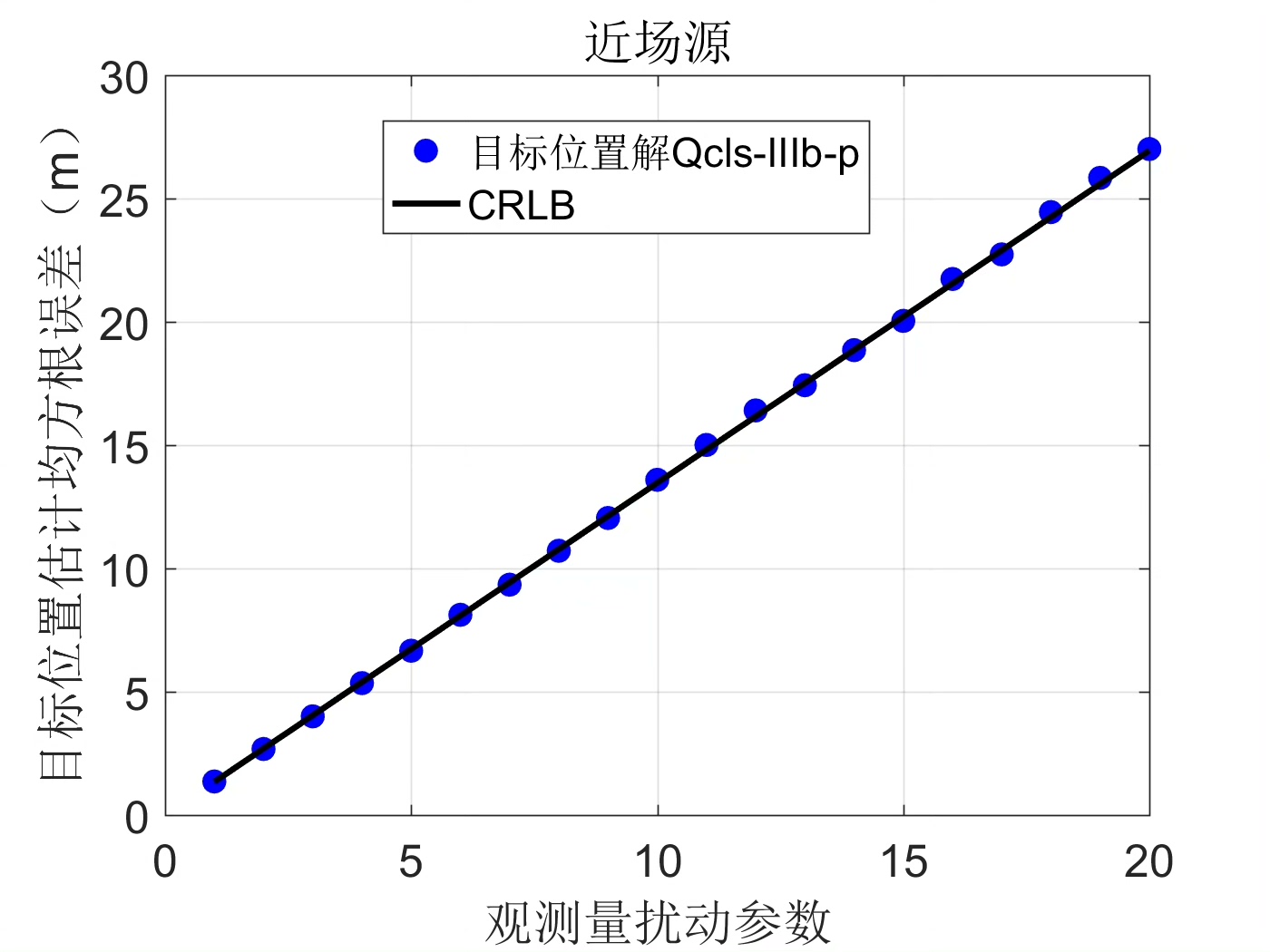
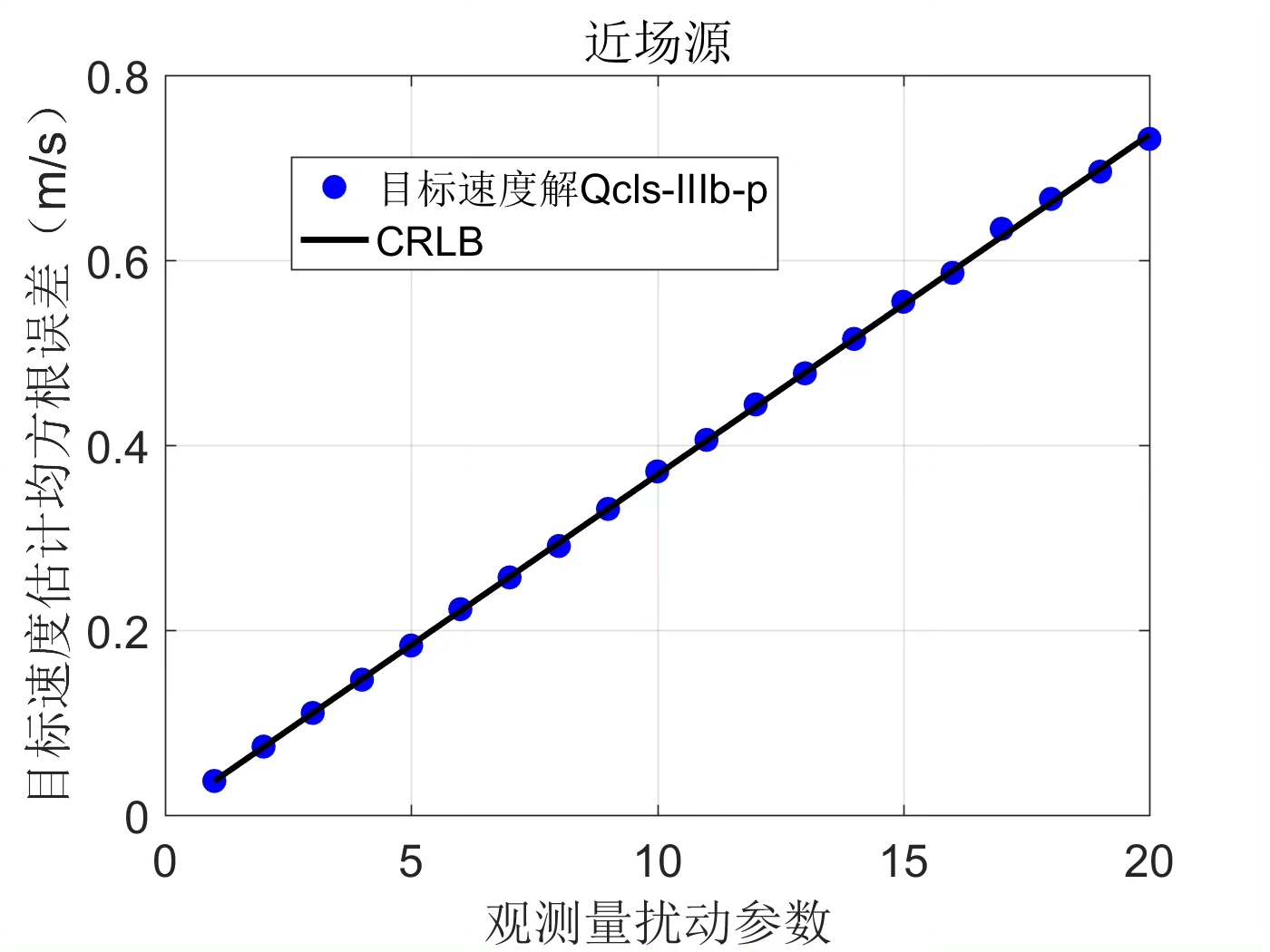
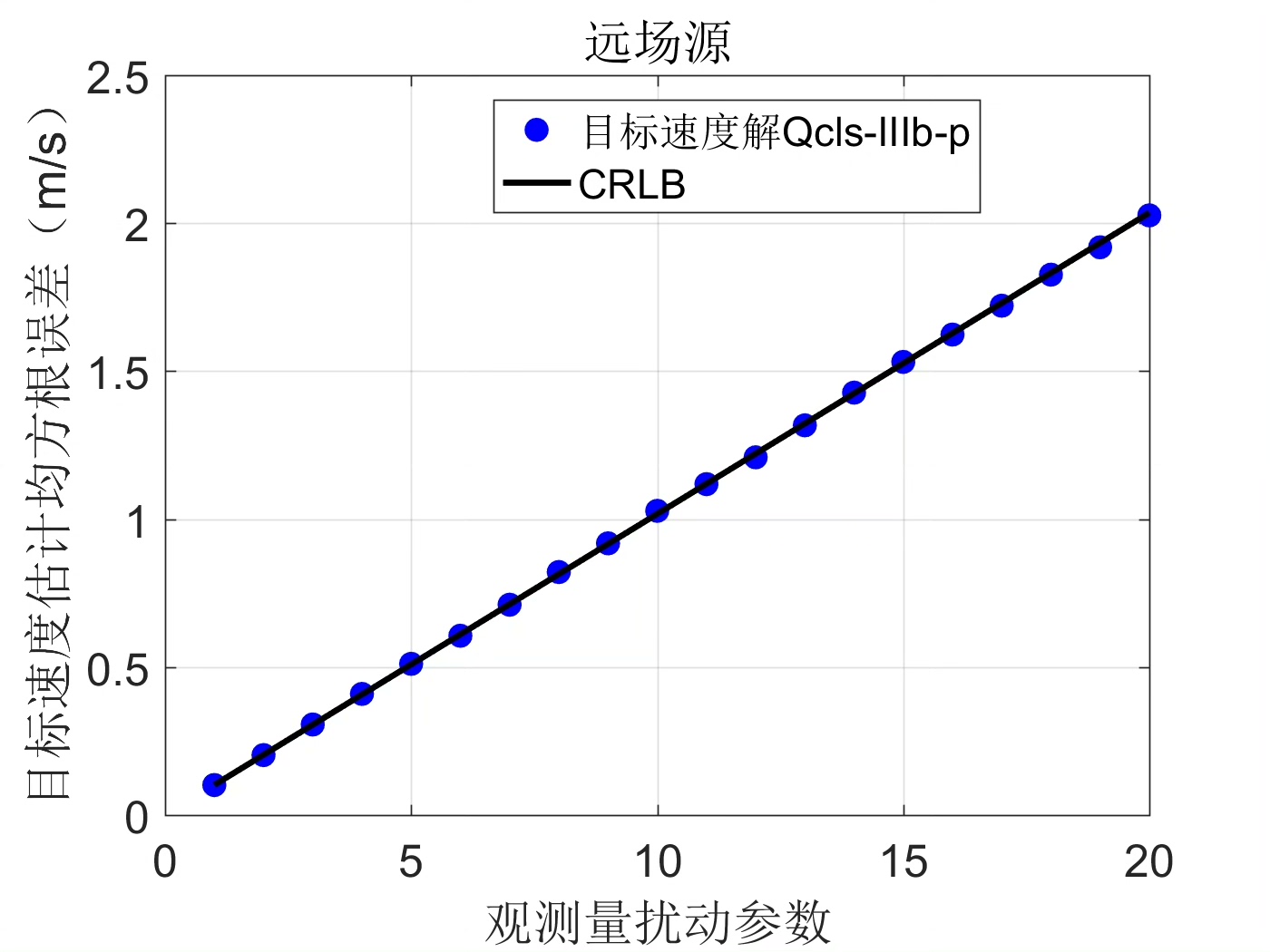
通过上述MATLAB仿真，我们可以初步验证基于TOA/FOA的无源定位方法在二次等式约束下的可行性。当然，实际应用中还需要进一步优化算法，考虑更多实际因素如多径效应、非视距传播等，以提高定位精度和可靠性。希望本文的内容能为大家在相关领域的研究和实践提供一些有益的参考。

希望这篇博文能帮助你更好地理解基于TOA/FOA的无源定位方法及其MATLAB仿真实现。如果你有任何问题或建议，欢迎在评论区留言交流。