考虑外层积分上限为虚数单位的平方的情况，
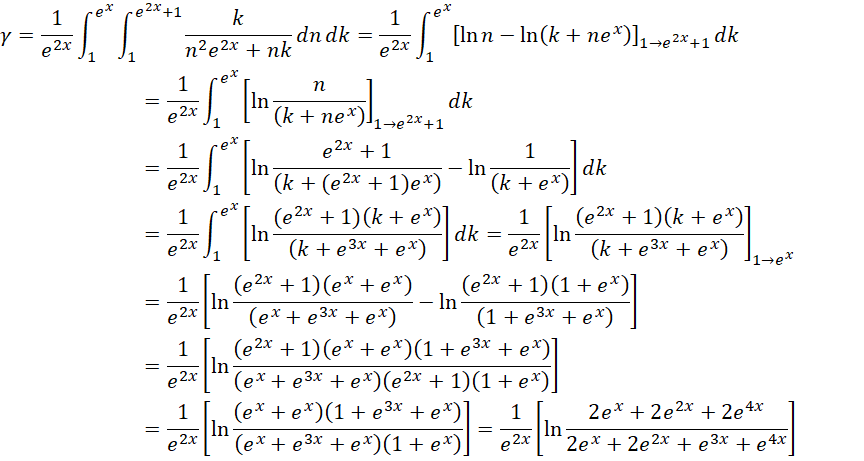
考虑完全用两个周期的情况，也就是积分上限都为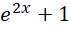
，
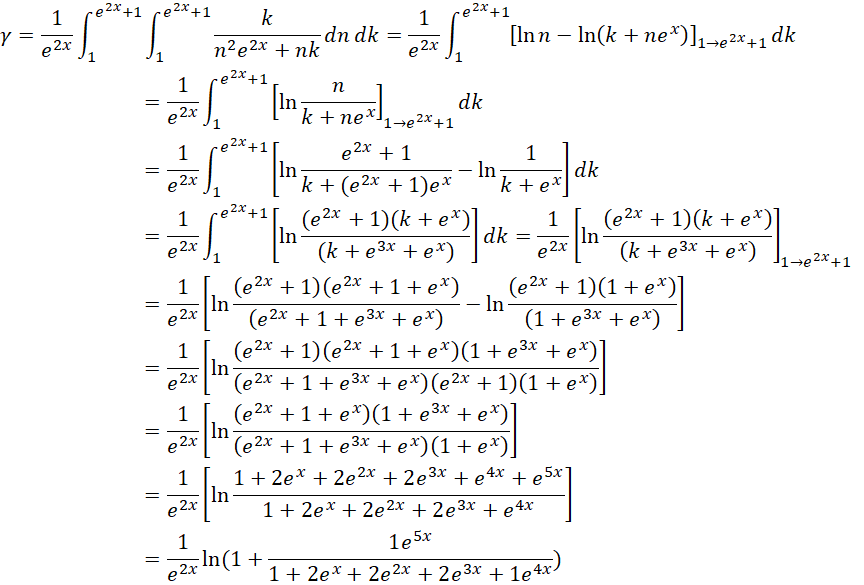
当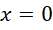
的时候，
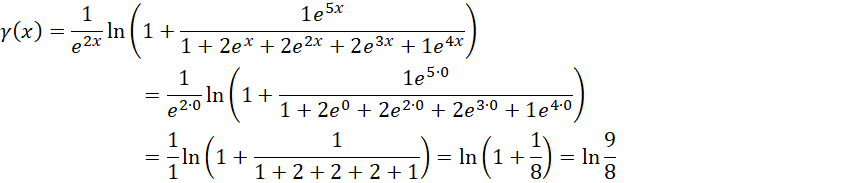
从函数图像，
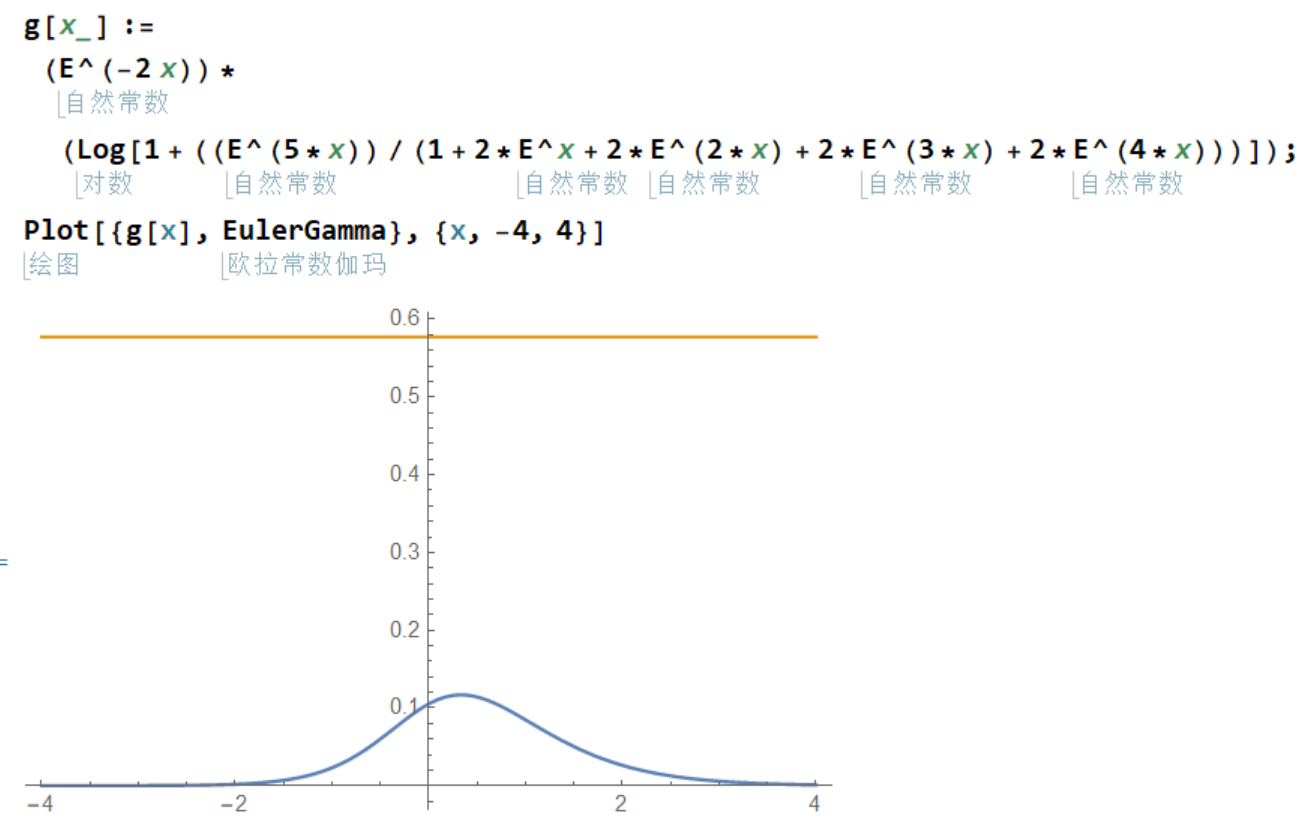
可以看出，这个形式比先前的形式更好，其最大值，
在，
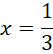
处，
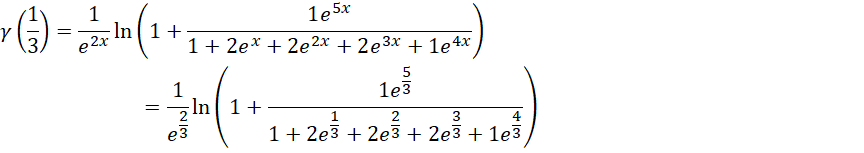
得到，
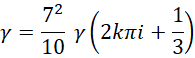
积分上限增加1，相当于极限点平移了
，另外这个数值的精度不如先前的好。
考虑两个都是不完全周期，
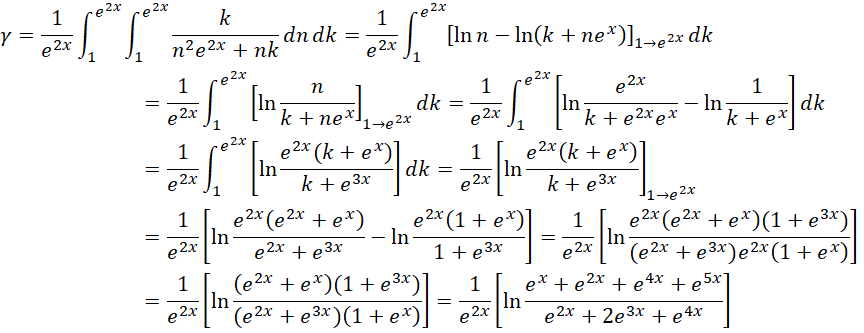
当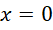
，
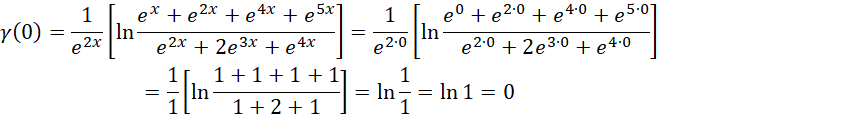
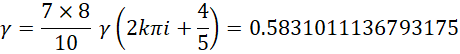
再考虑内小外大的情况，
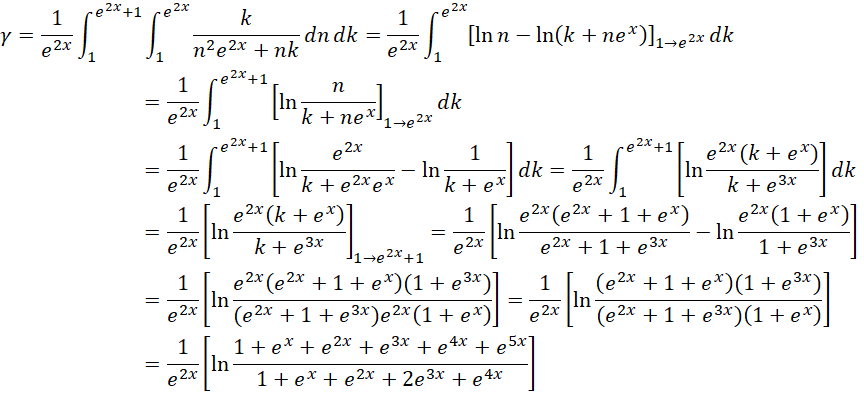
当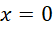
，
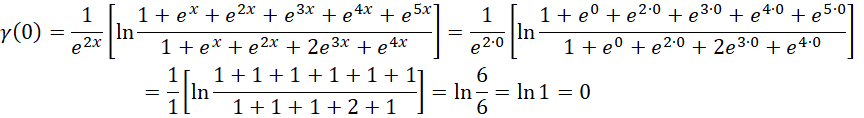
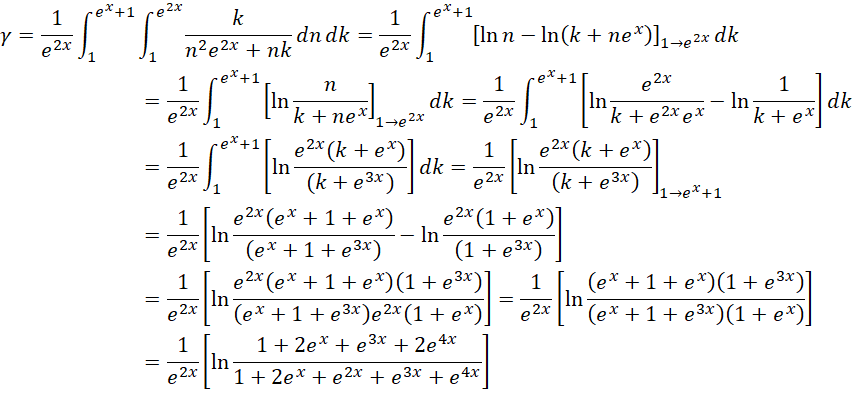
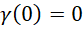
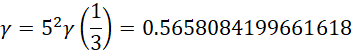
在考虑过各种情况之后，可以认识到，欧拉常数存在的意义，在于方程的虚数单位周期和数量本身的无限可分之间的矛盾的体现。微分的本质要求数量无限可分，无限可分也是实际的情况，但是方程能够写出，则自动产生了数量层级之间的差异以及因为虚数单位的存在而造成的周期性。整数和有理数都是这种周期性存在的体现，对于整数来说，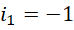
作为虚数单位，即可处理大多数整数之间的运算问题，而涉及到质数，则需要
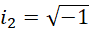来处理。在讨论哥德巴赫猜想的时候，这一点已经明确了。用于计算质数或者其倒数全乘积的黎曼泽塔函数，用复数可以处理它的大多数性质，但是，
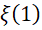和它对应的连续形式lnx 
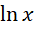之间的差异，就使得用复数处理失去了精度，哪怕是用，
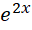作为虚数单位，也不能得到足够精度的结果。这说明，充分连续的数学对象，和用来度量的数字系统之间总是存在微小的差异。数学对象用以描述真实世界，而这种真实在于其无限的精度，但是数字总是有最小间隔，以至于数字系统总是基于有限精度，即便增加了周期性的复数，仍然不能保证两个系统之间具有相同的精度，也就是说，两位多分复数并不能处理这种精度差异，而是需要两个多分复数，它们之间的最小单位之间的比率可能仍然是一个复数，这个比率的变化将会决定最终计算的精度。从上面的分析不难看出，强制要求两种系统都以虚数单位的四次幂的倒数为共同最小单位，能够获得的十进制精度至多只有5位。所以我们需要的是两个不同的虚数单位，才能获得无限精度的表述方式。换句话说，就是自然中任何两个系统之间的精度都可能是完全不同的，就像不同的惯性系有着不同的虚数单位。而试着统一虚数单位的做法本质上是不成立的。那么，一个基于连续性的数学对象，其实就是一个虚数单位自身可变的数学对象，或者说，完全不受到虚数单位大小束缚的数学对象，比如对倒数积分之后的对数函数。换句话说，以上尝试必然都是失败的，唯一能成功的做法，就是像处理相对论问题那样，使用两个不同的虚数单位，并且通过调节两个不同的虚数单位的比值，决定最终的精度的数字位数。