一、引言
算法是个很有意义的课题,尽管大模型让我们不需要像以前学习机器学习那样,需要很深的数学基础,但结合算法来应用大模型确实是个很有趣的事情,传统算法经过数十年发展,已在路径规划、优化计算等领域达到极高的精确度;另一方面,大语言模型的崛起让人机交互变得前所未有的自然流畅。然而,一个不容忽视的现实是:再精确的算法,如果用户看不懂、不会用,就只是实验室里的玩具;再流畅的表达,如果缺乏技术可靠性,就只是华丽的空谈。
想象这样一个场景:导航系统为你计算出了一条理论上最优的路线,却只能用一串坐标告诉你怎么走;或者,一个能言善道的助手热情地为你指路,却把你带进了死胡同。这两种情况,本质上都是技术能力与用户体验之间的断裂。这种断裂并非偶然,而是单一技术路线的固有局限。算法擅长计算却不善表达,模型善于沟通却难以精确,各有所长,也各有所短。因此,真正的突破不在于让某一方变得更强大,而在于让两者形成互补协作的关系,用各自的长处弥补对方的短板。
这是我们今天想探讨得A*算法与大模型融合的核心价值所在。A*算法如同精密的"空间计算大脑",保证路径的数学最优性;大模型则如同清晰的"表达嘴巴",让算法结果变得可理解、可执行。二者结合,才能跨越技术与用户之间的鸿沟,打造出真正可用的智能导航系统,既有数学的严谨,又有人文的温度。

二、基础介绍
1. A* 算法
1.1 算法介绍:
A* 算法是整个智能导航系统的计算核心,数学层面的最优路径搜索,负责在复杂的图结构或空间网格中进行启发式搜索,找到从起点到终点的最优路径。它通过评估函数智能地探索搜索空间:
f(n) = g(n) + h(n)
其中 :
- g(n): 代表从起点到当前节点的实际代价;
- h(n): 代表从当前节点到目标点的估计代价,重要的启发函数;
- f(n):总代价,A* 每次选 f (n) 最小的节点走;
这一算法的核心价值在于保证路径的数学最优性,无论是追求最短距离、最快时间还是最省资源,A* 都能在满足约束条件的前提下找到理论上的最优解。它像一位精密的数学家,默默计算着每一个可能的路径组合,确保最终输出的路线在技术层面是无懈可击的。
然而,A* 算法的输出本质上是冷冰冰的坐标序列或节点列表。它知道怎么走最优,却无法解释为什么这样走,更无法用人类自然的方式告诉用户"前方路口右转,看到红色建筑后直行"。这就是它的局限,精于计算,拙于表达。
1.2 A* 算法的最优说明:
- 只要启发函数h(n) 满足可采纳性,即永远不大于真实代价,A*就一定能找到最短路径,且效率远高于暴力搜索。
1.3 最常用启发函数:
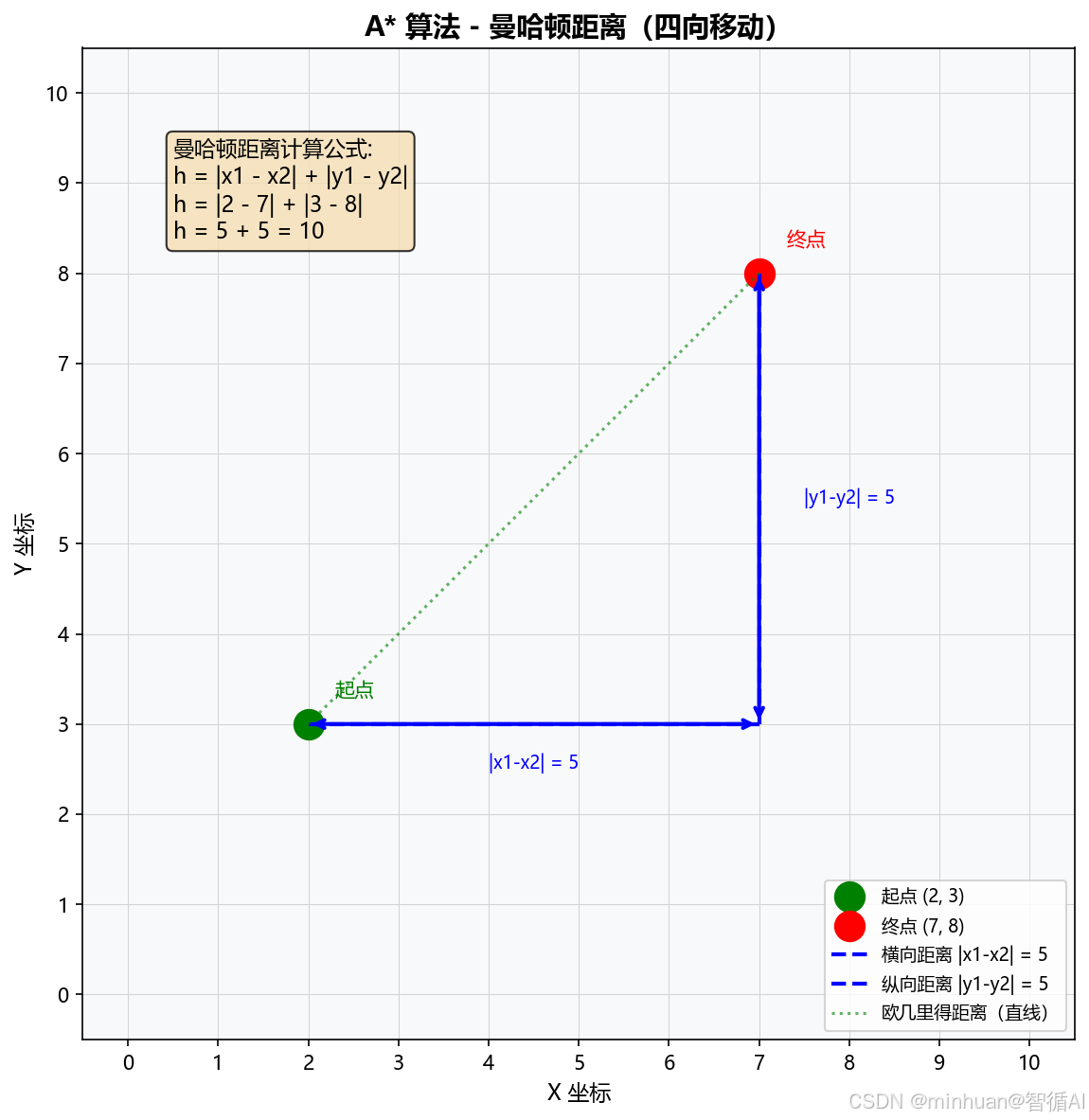
- 1. 网格地图(四向移动):曼哈顿距离
- 适用场景:只能上下左右四个方向移动的网格地图
- 计算公式:h = |x₁ - x₂| + |y₁ - y₂|
- 含义说明:横向距离差的绝对值 + 纵向距离差的绝对值
- 示例:
- 起点坐标:(2, 3)
- 终点坐标:(7, 8)
- 启发值 h = |2-7| + |3-8| = 5 + 5 = 10
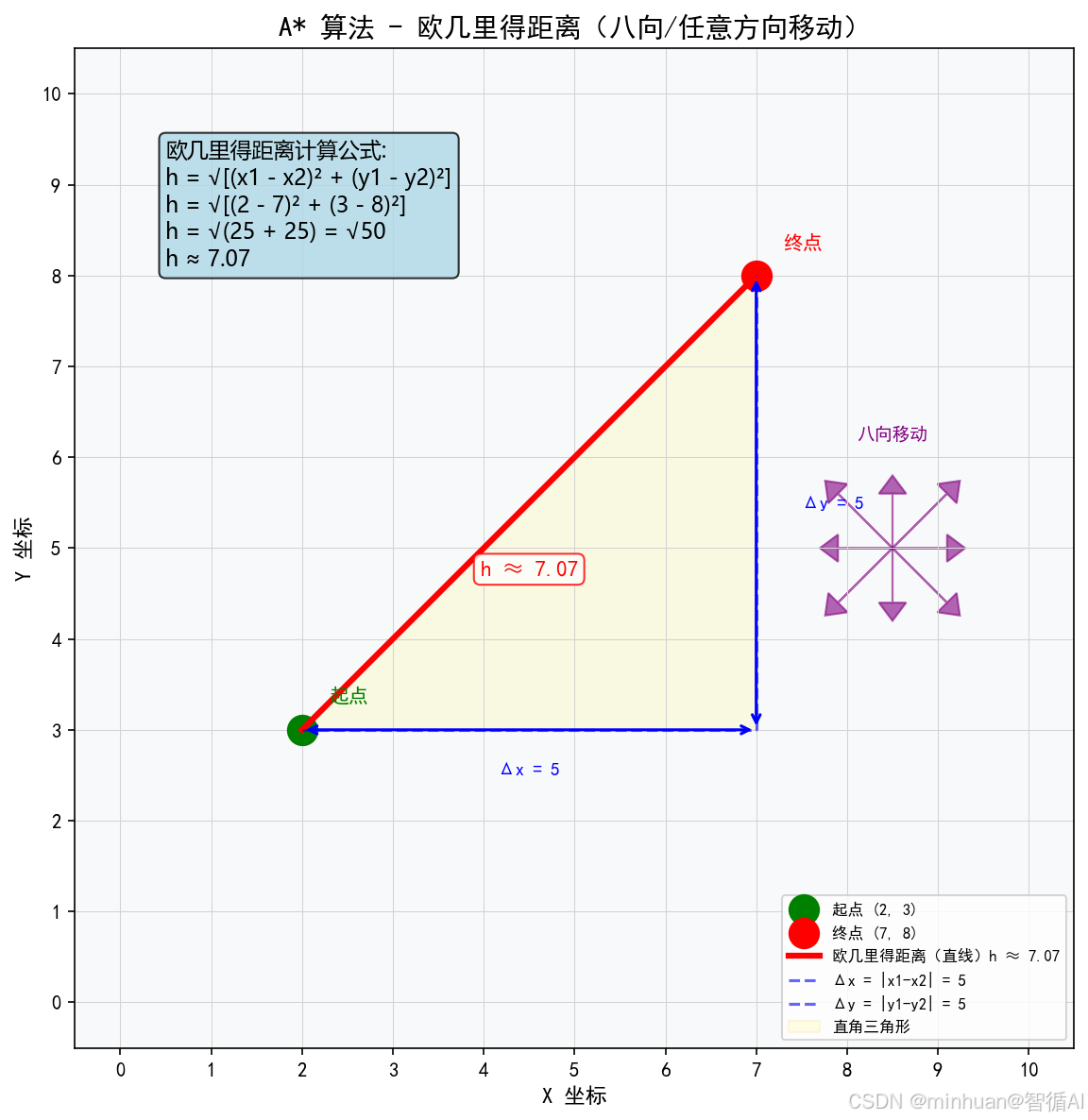
- 2. 网格地图(八向/任意方向):欧几里得距离
- 适用场景:可以向八个方向或任意角度移动的地图
- 计算公式:h = √[(x₁ - x₂)² + (y₁ - y₂)²]
- 含义说明:两点之间直线距离的平方根
- 示例:
- 起点坐标:(2, 3)
- 终点坐标:(7, 8)
- 启发值 h = √[(2-7)² + (3-8)²] = √(25 + 25) = √50 ≈ 7.07
- **核心原则:**启发函数 h(n) 必须≤实际代价,才能保证 A* 找到最优路径,即启发函数需满足可采纳性
1.4 A* 算法完整执行流程:

流程说明:
-
- 初始化起点、终点、障碍物地图
-
- 维护两个集合:
- open list:待检查的节点
- closed list:已经检查过的节点
-
- 把起点加入 open list
-
- 循环:
- 从 open list 中选出 f (n) 最小的节点作为当前节点
- 把当前节点移入 closed list
- 如果当前节点是终点 → 回溯得到完整路径
- 遍历当前节点的上下左右 / 八邻域邻居
- 对每个有效邻居:
- 不在 closed list 且不是障碍物
- 计算新的 g、h、f
- 若更优,则更新父节点、加入 open list
-
- 回溯父节点,从终点倒推回起点 → 得到最优路径
2. 大模型加持
大模型是整个智能导航系统的交互核心,基于自然语言层面的路径解释,负责将 A* 算法输出的结构化路径数据转化为人类可理解、可执行的自然语言指令。它能够理解用户的意图,将抽象的坐标和步骤转化为流畅的导航描述,并能根据上下文进行多轮对话交互。
大模型的核心价值在于降低技术门槛,让算法结果"能用、易懂":
- 它可以将"坐标点序列 [(116.4, 39.9), (116.41, 39.91), ...]"转化为"从当前位置出发,
- 沿主干道向北行驶约 5 公里,在第二个红绿灯路口左转,
- 看到加油站后继续直行 200 米即达目的地"。
这种转化不仅仅是语言风格的改变,更是人机交互体验的本质提升。但大模型也有其局限,它可能产生幻觉,数值计算不够精确,无法保证路径的数学最优性。因此,它需要与精确算法配合使用,而非独立承担路径规划的核心计算任务。
3. 组合价值
3.1 算法 = 大脑的空间计算
纯算法的痛点,A* 只会输出:
- 坐标序列:(0,0) → (1,0) → (2,1) → ...
- 步骤编号:Step1、Step2、Step3
不利于理解,既看不懂,也用不了,此时的算法价值体现:
- A* 算法如同系统的大脑,负责所有需要精确计算和逻辑推理的任务。
- 它在后台默默工作,处理复杂的空间关系、代价函数和优化目标,确保每一条推荐路径都经得起数学验证。
- 没有这个"大脑",系统就失去了精确性和可靠性。
3.2 大模型 = 嘴巴的清晰表达
- 大模型如同系统的嘴巴,负责将所有计算结果以人类友好的方式表达出来。
- 它理解用户的语言,回应用户的疑问,并根据不同用户的表达习惯调整输出风格。
- 没有这个"嘴巴",再精确的计算结果也无法被用户有效理解和使用。
简而言之,大模型做这 4 件事:
-
- 把路径坐标 → 自然语言导航例:向右走2格,再向上走1格,绕过障碍物
-
- 把抽象任务 → 结构化步骤例:旅行规划、学习路径、解题流程
-
- 支持自然语言输入用户说:"帮我规划从家到公司的路线"
-
- 人性化解释为什么这么走?最近?最快?最省钱?
3.3 二者结合的必要性
- 只有大脑没有嘴巴:系统能算出最优路径,但用户看不懂、不会用,最终沦为算法玩具。
- 只有嘴巴没有大脑:系统能说会道,但给出的路线可能绕远、甚至无法通行,缺乏技术可靠性。
- 大脑 + 嘴巴结合:系统既能保证路径的数学最优性,又能让用户轻松理解和执行,这才是真正可用的智能导航系统。
A* + 大模型结合使用:
用户自然语言请求 → 大模型解析:起点、终点、约束、偏好 → A*算法计算最优路径↓大模型把路径翻译成可阅读、可执行的自然语言导航 → 返回给用户

4. 工作流
从用户请求到智能输出,整个系统的工作流程形成一条清晰的数据流转链路:

第一步:意图理解
- 用户发起自然语言请求,如"帮我规划一条从酒店到博物馆的路线,我想沿途看看老街"。
- 大模型首先进行意图识别,提取关键信息(起点、终点、偏好约束),将其转化为结构化查询参数。
第二步:路径计算
- 结构化参数传递给 A* 算法层,算法在地图数据中进行启发式搜索;
- 考虑距离、时间、用户偏好等多重因素,返回最优路径的坐标序列和关键节点信息。
第三步:结果解释
- 路径数据再次交由大模型进行自然语言生成,将坐标序列转化为流畅的导航指令;
- 并根据用户偏好添加个性化建议,如"沿途会经过百年老街,建议预留 30 分钟参观"。
第四步:交互反馈
- 用户可以通过多轮对话进一步调整需求,如"避开高速公路"或"想路过某家餐厅",系统会重新调用 A* 算法计算新路径;
- 并由大模型生成更新后的导航说明,形成完整的交互闭环。
三、整体执行流程
- 支持自然语言、结构化两种输入,大模型做解析;
- A* 负责核心计算,大模型负责交互和解释;
- 增加用户确认环节,支持大模型迭代优化解释结果。
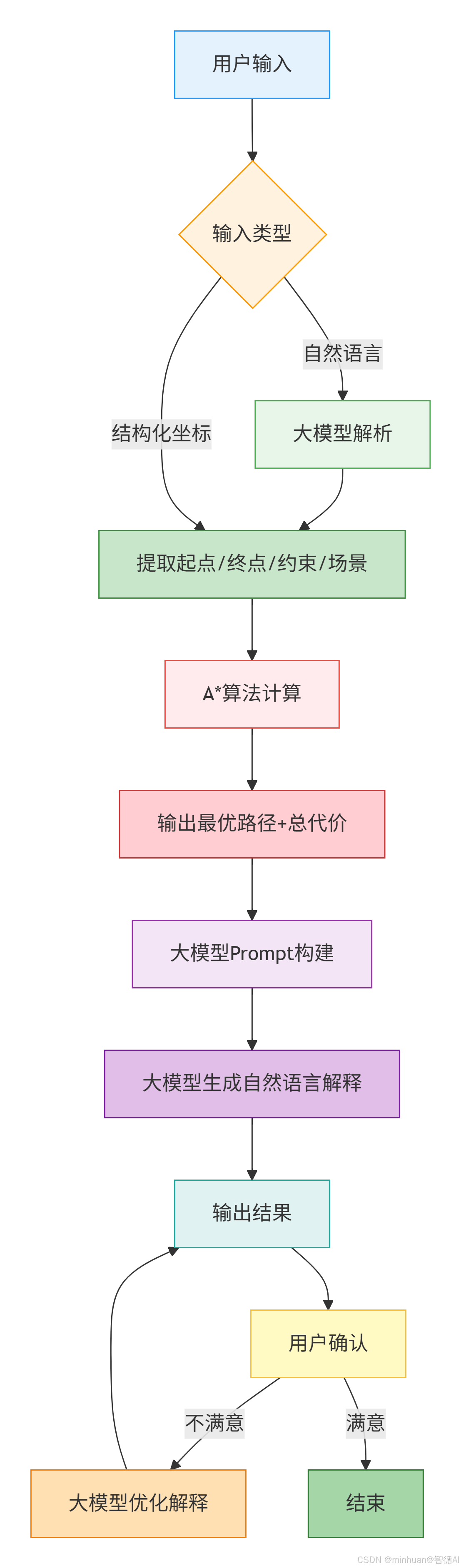
步骤说明:
-
- 用户输入:用户提交导航请求,可以是自然语言或结构化坐标
-
- 输入类型判断:自然语言 → 进入大模型解析;结构化坐标 → 直接进入路径计算
-
- 大模型解析:从自然语言中提取起点、终点、约束条件、场景信息
-
- A*算法计算:基于提取的信息进行最优路径搜索
-
- 输出路径+代价:返回最优路径坐标序列和总代价
-
- 大模型Prompt构建:为路径生成构建提示词模板
-
- 大模型生成解释:将路径数据转化为自然语言导航说明
-
- 输出结果:向用户展示导航结果
-
- 用户确认:满意 → 流程结束;不满意 → 大模型优化解释,重新生成
-
- 结束:用户确认满意后流程终止
四、示例分析
1. A* 算法基础示例
绕开障碍物探索左右路径;
python
import heapq
import matplotlib.pyplot as plt
import matplotlib.patches as patches
def manhattan(a, b):
return abs(a[0] - b[0]) + abs(a[1] - b[1])
def a_star(start, end, grid):
rows = len(grid)
cols = len(grid[0])
open_heap = []
heapq.heappush(open_heap, (0, start))
came_from = {}
g_score = {(i, j): float('inf') for i in range(rows) for j in range(cols)}
g_score[start] = 0
directions = [(-1, 0), (1, 0), (0, -1), (0, 1)]
while open_heap:
f_current, current = heapq.heappop(open_heap)
if current == end:
path = []
while current in came_from:
path.append(current)
current = came_from[current]
path.append(start)
return path[::-1]
for dx, dy in directions:
x = current[0] + dx
y = current[1] + dy
neighbor = (x, y)
if 0 <= x < rows and 0 <= y < cols:
if grid[x][y] == 1:
continue
tentative_g = g_score[current] + 1
if tentative_g < g_score[neighbor]:
came_from[neighbor] = current
g_score[neighbor] = tentative_g
f = tentative_g + manhattan(neighbor, end)
heapq.heappush(open_heap, (f, neighbor))
return None
if __name__ == "__main__":
# 0=可走, 1=障碍
grid = [
[0, 1, 0, 0, 0],
[0, 1, 0, 1, 0],
[0, 0, 0, 1, 0],
[0, 1, 1, 1, 0],
[0, 0, 0, 0, 0],
]
start = (0, 0)
end = (4, 4)
path = a_star(start, end, grid)
print("最优路径坐标:")
print(path)
# 设置中文字体
plt.rcParams['font.sans-serif'] = ['Microsoft YaHei', 'SimHei']
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['font.family'] = 'sans-serif'
# 创建图形
fig, ax = plt.subplots(figsize=(10, 10))
rows = len(grid)
cols = len(grid[0])
# 绘制网格
for i in range(rows):
for j in range(cols):
if grid[i][j] == 1:
# 障碍物 - 深灰色
rect = patches.Rectangle((j, rows-1-i), 1, 1,
linewidth=1, edgecolor='black',
facecolor='#555555')
ax.add_patch(rect)
else:
# 可行走区域 - 浅灰色
rect = patches.Rectangle((j, rows-1-i), 1, 1,
linewidth=1, edgecolor='black',
facecolor='#e0e0e0')
ax.add_patch(rect)
# 绘制路径
if path:
# 提取x,y坐标(注意y轴翻转)
path_x = [p[1] + 0.5 for p in path]
path_y = [rows - 1 - p[0] + 0.5 for p in path]
ax.plot(path_x, path_y, 'b-', linewidth=3, label='最优路径', alpha=0.8)
# 绘制路径箭头
for i in range(len(path) - 1):
x1, y1 = path[i][1] + 0.5, rows - 1 - path[i][0] + 0.5
x2, y2 = path[i+1][1] + 0.5, rows - 1 - path[i+1][0] + 0.5
dx, dy = x2 - x1, y2 - y1
ax.arrow(x1, y1, dx * 0.6, dy * 0.6,
head_width=0.15, head_length=0.15,
fc='blue', ec='blue', alpha=0.7)
# 绘制起点
ax.plot(start[1] + 0.5, rows - 1 - start[0] + 0.5, 'go',
markersize=20, label='起点', zorder=5)
ax.text(start[1] + 0.5, rows - 1 - start[0] + 0.5, '起点',
ha='center', va='center', fontsize=10, color='white',
fontweight='bold', fontfamily='Microsoft YaHei', zorder=6)
# 绘制终点
ax.plot(end[1] + 0.5, rows - 1 - end[0] + 0.5, 'ro',
markersize=20, label='终点', zorder=5)
ax.text(end[1] + 0.5, rows - 1 - end[0] + 0.5, '终点',
ha='center', va='center', fontsize=10, color='white',
fontweight='bold', fontfamily='Microsoft YaHei', zorder=6)
# 设置坐标轴
ax.set_xlim(0, cols)
ax.set_ylim(0, rows)
ax.set_aspect('equal')
ax.set_xticks(range(cols + 1))
ax.set_yticks(range(rows + 1))
ax.grid(True, alpha=0.3)
# 设置标题和标签
ax.set_title('A* 算法路径搜索可视化', fontsize=16,
fontweight='bold', fontfamily='Microsoft YaHei')
ax.set_xlabel('X 坐标', fontsize=12, fontfamily='Microsoft YaHei')
ax.set_ylabel('Y 坐标', fontsize=12, fontfamily='Microsoft YaHei')
# 添加图例
ax.legend(loc='upper left', fontsize=10)
# 添加说明文本
info_text = (
f"起点: {start}\n"
f"终点: {end}\n"
f"路径长度: {len(path) if path else 0}\n"
f"障碍物数量: {sum(row.count(1) for row in grid)}"
)
ax.text(cols - 0.2, rows - 0.2, info_text,
ha='right', va='top',
bbox=dict(boxstyle='round', facecolor='wheat', alpha=0.8),
fontsize=10, fontfamily='Microsoft YaHei')
plt.tight_layout()
plt.savefig('91.A算法_路径搜索可视化.png', dpi=150, bbox_inches='tight')
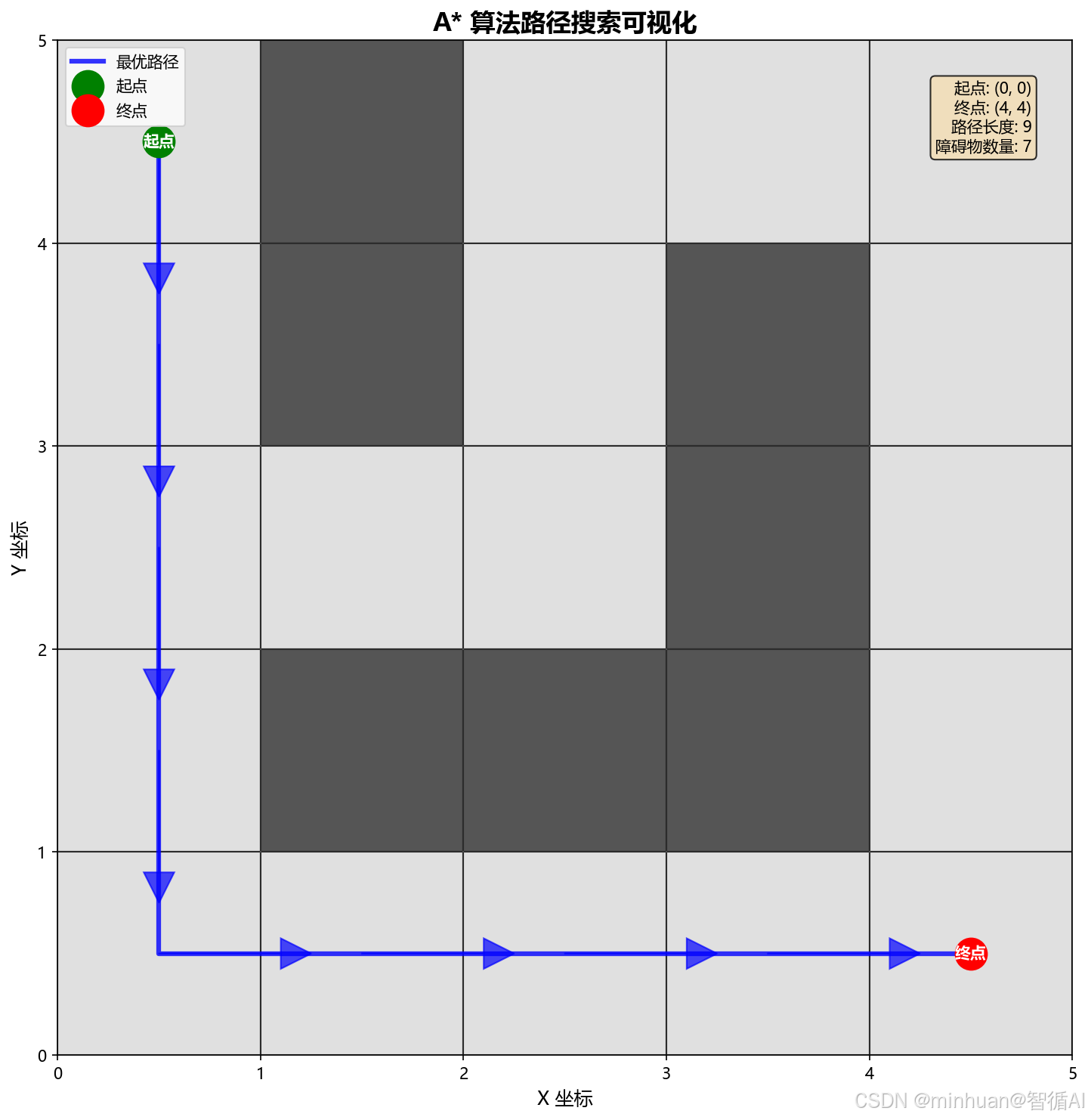
plt.show()输出结果:
最优路径坐标:
(0, 0), (1, 0), (2, 0), (3, 0), (4, 0), (4, 1), (4, 2), (4, 3), (4, 4)
结果图示:
2. 大模型融合实践
-
- A*路径规划引擎:实现带地形代价的A*算法,在网格地图中搜索最优路径。基础移动代价为1,山地等地形增加额外代价,障碍物不可通行,保证路径数学最优。
-
- 混元大模型集成:调用混元API将A*输出的坐标序列转化为自然语言导航。支持旅行规划、解题指导、任务流程三种场景,每种场景有定制化的Prompt模板。
-
- 路径可视化:使用Matplotlib绘制完整地图:白色=平地、黑色=障碍物、黄橙色=山路,蓝色线条标注最优路径,绿色/红色标记起点终点。
python
import os
import json
import matplotlib.pyplot as plt
import numpy as np
from openai import OpenAI
plt.rcParams['font.sans-serif'] = ['Microsoft YaHei', 'SimHei', 'Arial Unicode MS', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['font.family'] = 'sans-serif'
# 配置腾讯混元API
api_key = 'sk-*******************************gmm0sBVXvZ5NP8Ze'
client = OpenAI(
api_key=api_key,
base_url="https://api.hunyuan.cloud.tencent.com/v1",
)
def call_llm(prompt, model="hunyuan-lite"):
"""调用腾讯混元大模型生成自然语言导航"""
try:
completion = client.chat.completions.create(
model=model,
messages=[
{"role": "system", "content": "你是一个专业的路径解释助手,输出简洁、易懂、可执行的自然语言内容。"},
{"role": "user", "content": prompt}
],
temperature=0.3 # 低随机性,保证结果稳定
)
return completion.choices[0].message.content
except Exception as e:
return f"调用混元大模型失败: {str(e)}"
def build_llm_prompt(path, grid, cost_map, scene_type):
"""
构建大模型的Prompt,适配不同场景
:param path: A*输出的路径坐标列表
:param grid: 网格地图
:param cost_map: 代价地图
:param scene_type: 场景类型(travel/study/task)
:return: 结构化Prompt
"""
# 1. 路径解析:把坐标转化为"步骤+方向+代价"
path_steps = []
for i in range(1, len(path)):
prev = path[i-1]
curr = path[i]
# 方向判断
if curr[0] > prev[0]:
direction = "向下(北)"
elif curr[0] < prev[0]:
direction = "向上(南)"
elif curr[1] > prev[1]:
direction = "向右(东)"
elif curr[1] < prev[1]:
direction = "向左(西)"
# 代价计算:基础代价1 + 地形额外代价
base_cost = 1
terrain_cost = cost_map[curr[0]][curr[1]]
step_cost = base_cost + terrain_cost
path_steps.append({
"步骤": i,
"从": prev,
"到": curr,
"方向": direction,
"基础代价": base_cost,
"地形代价": terrain_cost,
"单步总代价": step_cost
})
# 2. 场景化Prompt
scene_prompts = {
"travel": f"""
你是旅行规划助手,请根据以下A*算法计算的最优路径,生成自然语言旅行导航:
1. 地图说明:0=平地(易走),1=障碍物(不可走),代价>0=山路(难走);
2. 路径步骤:{path_steps};
3. 总代价:{sum([s['单步总代价'] for s in path_steps])};
要求:
- 用口语化的旅行导航语言,避免坐标;
- 提示山路/障碍等注意事项;
- 给出总行程和难度评价;
- 示例格式:
「从起点出发,先向北走200米(平地),再向东绕开障碍物,接着向东北走500米(山路,注意防滑),最终到达终点。全程约700米,难度中等。」
""",
"study": f"""
你是解题步骤助手,请根据以下A*算法计算的最优解题路径,生成自然语言解题指导:
1. 路径步骤:{path_steps}(每个坐标代表一个解题状态,步骤代表推理环节);
2. 代价说明:代价越高,该步骤难度越大;
要求:
- 把抽象步骤转化为"解题思路+具体操作";
- 标注高难度步骤的注意事项;
- 示例格式:
「解题第一步:先梳理已知条件(难度低),第二步:推导中间公式(难度中等),第三步:代入数值计算(难度高,注意单位换算),最终得到答案。」
""",
"task": f"""
你是任务流程助手,请根据以下A*算法计算的最优任务路径,生成自然语言任务清单:
1. 路径步骤:{path_steps}(每个坐标代表一个任务节点,步骤代表执行顺序);
2. 代价说明:代价越高,该任务耗时/成本越高;
要求:
- 按优先级排序,标注每个任务的耗时/成本;
- 提示避开"障碍物"(风险点);
- 示例格式:
「任务1:收集需求(耗时1小时,低成本)→ 任务2:设计方案(耗时3小时,中成本,避开需求变更风险)→ 任务3:落地执行(耗时5小时,高成本)→ 完成。」
"""
}
return scene_prompts[scene_type]
def visualize_path(grid, path, cost_map, start, end):
"""
可视化A*算法找到的路径
:param grid: 网格地图
:param path: 路径坐标列表
:param cost_map: 代价地图
:param start: 起点坐标
:param end: 终点坐标
"""
fig, ax = plt.subplots(figsize=(10, 10))
# 转换为numpy数组方便处理
grid_array = np.array(grid)
cost_array = np.array(cost_map)
# 创建颜色映射
# 0=平地(白色), 1=障碍物(黑色), >0=山路(渐变黄到橙)
color_grid = np.zeros_like(grid_array, dtype=float)
for i in range(len(grid_array)):
for j in range(len(grid_array[0])):
if grid_array[i][j] == 1:
color_grid[i][j] = 1.0 # 障碍物
elif cost_array[i][j] > 0:
color_grid[i][j] = 0.5 + cost_array[i][j] * 0.1 # 山路渐变
# 绘制网格背景
cmap = plt.cm.colors.ListedColormap(['white', 'lightyellow', 'orange', 'red'])
ax.imshow(color_grid, cmap=cmap, origin='upper', interpolation='nearest')
# 绘制网格线
for i in range(len(grid_array) + 1):
ax.axhline(i - 0.5, color='gray', linewidth=0.5, alpha=0.3)
ax.axvline(i - 0.5, color='gray', linewidth=0.5, alpha=0.3)
# 标注代价数值
for i in range(len(grid_array)):
for j in range(len(grid_array[0])):
if grid_array[i][j] == 0:
if cost_array[i][j] > 0:
ax.text(j, i, f'代价:{cost_array[i][j]}',
ha='center', va='center', fontsize=8, color='red')
# 绘制路径
if path and len(path) > 1:
path_array = np.array(path)
ax.plot(path_array[:, 1], path_array[:, 0], 'b-', linewidth=3,
label='最优路径', alpha=0.8)
# 绘制路径节点
ax.scatter(path_array[:, 1], path_array[:, 0], c='blue', s=100,
zorder=5, edgecolors='white', linewidth=2)
# 标记起点和终点
ax.scatter(start[1], start[0], c='green', s=300, marker='o',
label='起点', zorder=10, edgecolors='black', linewidth=2)
ax.text(start[1], start[0], '起点', ha='center', va='center',
fontsize=10, fontweight='bold', color='white', zorder=11)
ax.scatter(end[1], end[0], c='red', s=300, marker='s',
label='终点', zorder=10, edgecolors='black', linewidth=2)
ax.text(end[1], end[0], '终点', ha='center', va='center',
fontsize=10, fontweight='bold', color='white', zorder=11)
# 添加图例和标题
ax.legend(loc='upper left', fontsize=12, framealpha=0.9)
ax.set_title('A*算法路径规划可视化\n白色=平地 | 黑色=障碍物 | 黄色/橙色=山路', fontsize=14, pad=20)
ax.set_xlabel('X坐标', fontsize=12)
ax.set_ylabel('Y坐标', fontsize=12)
ax.grid(True, alpha=0.3)
# 调整布局
plt.tight_layout()
# 保存图片
plt.savefig('A星算法路径可视化.png', dpi=300, bbox_inches='tight')
print(f"\n图片已保存为: A星算法路径可视化.png")
plt.show()
plt.close()
# ------------- 完整流程测试 -------------
if __name__ == "__main__":
# 先定义A*算法(需要导入或实现)
import heapq
def a_star_advanced(start, end, grid, cost_map):
"""
A*算法实现,考虑地形代价
:param start: 起点坐标
:param end: 终点坐标
:param grid: 地图网格
:param cost_map: 代价地图
:return: 路径列表, 总代价
"""
def heuristic(a, b):
return abs(a[0] - b[0]) + abs(a[1] - b[1])
open_set = []
heapq.heappush(open_set, (0 + heuristic(start, end), 0, start))
came_from = {}
g_score = {start: 0}
cost = {start: 1}
while open_set:
_, current_g, current = heapq.heappop(open_set)
if current == end:
path = []
while current in came_from:
path.append(current)
current = came_from[current]
path.append(start)
path.reverse()
return path, g_score[end]
for dx, dy in [(0, 1), (1, 0), (0, -1), (-1, 0)]:
neighbor = (current[0] + dx, current[1] + dy)
if 0 <= neighbor[0] < len(grid) and 0 <= neighbor[1] < len(grid[0]):
if grid[neighbor[0]][neighbor[1]] == 1:
continue
new_cost = 1 + cost_map[neighbor[0]][neighbor[1]]
tentative_g_score = g_score[current] + new_cost
if neighbor not in g_score or tentative_g_score < g_score[neighbor]:
came_from[neighbor] = current
g_score[neighbor] = tentative_g_score
f_score = tentative_g_score + heuristic(neighbor, end)
heapq.heappush(open_set, (f_score, tentative_g_score, neighbor))
return None, float('inf')
# 1. 定义地图和代价
grid = [
[0, 1, 0, 0, 0, 0, 0],
[0, 1, 0, 1, 0, 1, 0],
[0, 0, 0, 1, 0, 1, 0],
[0, 1, 1, 1, 0, 1, 0],
[0, 0, 0, 0, 0, 1, 0],
[0, 1, 1, 1, 1, 1, 0],
[0, 0, 0, 0, 0, 0, 0]
]
cost_map = [
[0, 0, 0, 0, 0, 0, 0],
[0, 0, 2, 0, 2, 0, 0],
[0, 2, 0, 0, 2, 0, 0],
[0, 0, 0, 0, 2, 0, 0],
[0, 2, 2, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0],
[0, 0, 2, 2, 0, 2, 0]
]
start = (0, 0)
end = (6, 6)
# 2. 执行A*算法
path, total_cost = a_star_advanced(start, end, grid, cost_map)
if path:
print(f"\n=== A*算法计算结果 ===")
print(f"路径: {path}")
print(f"总代价: {total_cost}")
# 3. 输出总代价计算过程
print(f"\n=== 总代价计算过程 ===")
total_calculated = 0
for i in range(1, len(path)):
prev = path[i-1]
curr = path[i]
# 方向判断
if curr[0] > prev[0]:
direction = "向下(北)"
elif curr[0] < prev[0]:
direction = "向上(南)"
elif curr[1] > prev[1]:
direction = "向右(东)"
else:
direction = "向左(西)"
base_cost = 1
terrain_cost = cost_map[curr[0]][curr[1]]
step_cost = base_cost + terrain_cost
total_calculated += step_cost
print(f"步骤{i}: 从{prev} 到{curr} ({direction})")
print(f" └─ 基础移动代价: {base_cost} + 地形额外代价: {terrain_cost} = 单步代价: {step_cost}")
print(f"\n总代价 = {total_calculated}")
print(f"(验证: {total_calculated} == {total_cost} -> {'✓ 通过' if total_calculated == total_cost else '✗ 失败'})")
# 4. 可视化路径
visualize_path(grid, path, cost_map, start, end)
# 5. 构建旅行场景的Prompt
prompt = build_llm_prompt(path, grid, cost_map, "travel")
# 6. 调用混元大模型
llm_response = call_llm(prompt)
# 7. 输出结果
print("\n=== 混元大模型自然语言导航 ===")
print(llm_response)
else:
print("未找到可行路径")Prompt 工程要点:
- 结构化输入:把 A * 的路径、代价、障碍物等信息结构化,避免大模型误解;
- 场景化指令:不同场景用不同的语言风格(旅行 = 口语化,解题 = 专业,任务 = 结构化);
- 低温度参数:temperature=0.1~0.3,保证输出稳定(路径解释需准确,而非创意)。
大模型输出校验:
- 增加 "事实校验" 环节:让大模型输出后,核对路径步骤是否与 A * 结果一致;
- 示例校验 Prompt:"请检查你输出的导航步骤是否与路径坐标 {path} 一致,若不一致请修正。"
输出结果:
=== A*算法计算结果 ===
路径: [(0, 0), (1, 0), (2, 0), (3, 0), (4, 0), (5, 0), (6, 0), (6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)]
总代价: 18
=== 总代价计算过程 ===
步骤1: 从(0, 0) 到(1, 0) (向下(北))
└─ 基础移动代价: 1 + 地形额外代价: 0 = 单步代价: 1
步骤2: 从(1, 0) 到(2, 0) (向下(北))
└─ 基础移动代价: 1 + 地形额外代价: 0 = 单步代价: 1
步骤3: 从(2, 0) 到(3, 0) (向下(北))
└─ 基础移动代价: 1 + 地形额外代价: 0 = 单步代价: 1
步骤4: 从(3, 0) 到(4, 0) (向下(北))
└─ 基础移动代价: 1 + 地形额外代价: 0 = 单步代价: 1
步骤5: 从(4, 0) 到(5, 0) (向下(北))
└─ 基础移动代价: 1 + 地形额外代价: 0 = 单步代价: 1
步骤6: 从(5, 0) 到(6, 0) (向下(北))
└─ 基础移动代价: 1 + 地形额外代价: 0 = 单步代价: 1
步骤7: 从(6, 0) 到(6, 1) (向右(东))
└─ 基础移动代价: 1 + 地形额外代价: 0 = 单步代价: 1
步骤8: 从(6, 1) 到(6, 2) (向右(东))
└─ 基础移动代价: 1 + 地形额外代价: 2 = 单步代价: 3
步骤9: 从(6, 2) 到(6, 3) (向右(东))
└─ 基础移动代价: 1 + 地形额外代价: 2 = 单步代价: 3
步骤10: 从(6, 3) 到(6, 4) (向右(东))
└─ 基础移动代价: 1 + 地形额外代价: 0 = 单步代价: 1
步骤11: 从(6, 4) 到(6, 5) (向右(东))
└─ 基础移动代价: 1 + 地形额外代价: 2 = 单步代价: 3
步骤12: 从(6, 5) 到(6, 6) (向右(东))
└─ 基础移动代价: 1 + 地形额外代价: 0 = 单步代价: 1
总代价 = 18
(验证: 18 == 18 -> ✓ 通过)
图片已保存为: A星算法路径可视化.png
=== 混元大模型自然语言导航 ===
「从起点开始,先向北走100米(平地),然后一直向北走500米(山路,小心路滑),最后向东走100米就到了。整个行程大概700米,难度算是中等哦!」
结果图示:
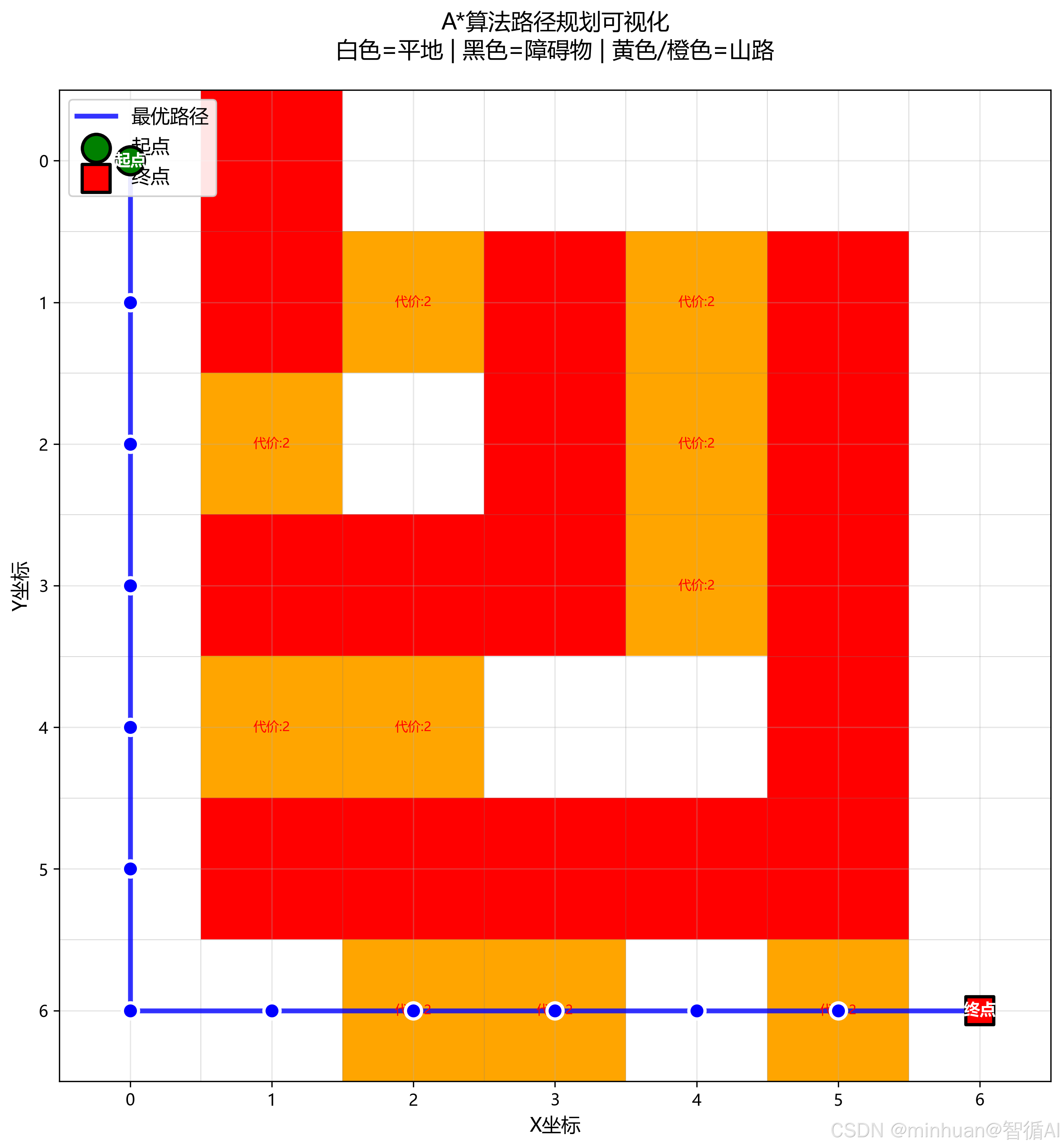
五、总结
A*算法和大模型的结合,核心就是互补,A*算法负责把事做对,找最最优的路径,算得准、不跑偏,但它输出的那些坐标,普通人看了一脸懵;大模型就负责把事说清,不用复杂术语,把冰冷的坐标变成能直接照着走的话,让算法真正能用起来,而不是藏在代码里的玩具。算法我们经历的也很多,其实不用一味追求算法多复杂,也不用觉得大模型多高深,能落地、能解决实际问题才最重要。
结合今天的示例,先跑通基础流程,把 A*算法的路径算出来,再用现成的大模型模板,把路径翻译成自然语言,先实现核心功能,再慢慢打磨细节。另外,Prompt 一定要写规范,别直接丢坐标给大模型,先做好路径预处理,这样大模型输出的内容才准、才实用。总的来说,二者结合的关键,就是让算法的理性和大模型的感性结合起来,既保证路径最优,又保证普通人能看懂、能用好,这才是这种技术融合的真正意义。