考研408--数据结构--day15--排序&内部排序（上）

（以下内容全部出自上述课程）

排序
- [1. 什么是排序](#1. 什么是排序)
- [2. 排序算法的应用](#2. 排序算法的应用)
- [3. 排序算法的评价指标](#3. 排序算法的评价指标)
- [4. 排序算法的分类](#4. 排序算法的分类)
- [5. 小结](#5. 小结)
内部排序
- [1. 插入排序](#1. 插入排序)
- - [1.1 算法思想](#1.1 算法思想)
  - [1.2 算法实现](#1.2 算法实现)
  - [1.3 算法效率分析](#1.3 算法效率分析)
  - [1.4 优化--折半插入排序](#1.4 优化--折半插入排序)
  - - [1.4.1 第一次查找](#1.4.1 第一次查找)
    - [1.4.2 第二次查找](#1.4.2 第二次查找)
    - [1.4.3 最终结果](#1.4.3 最终结果)
    - [1.4.4 稳定&代码](#1.4.4 稳定&代码)
  - [1.5 对链表进行插入排序](#1.5 对链表进行插入排序)
  - [1.6 小结](#1.6 小结)
- [2. 希尔排序](#2. 希尔排序)
- - [2.1 过程](#2.1 过程)
  - - [2.1.1 第一趟](#2.1.1 第一趟)
    - [2.1.2 第二趟](#2.1.2 第二趟)
    - [2.1.3 第三趟](#2.1.3 第三趟)
    - [2.1.4 小结](#2.1.4 小结)
  - [2.2 算法实现](#2.2 算法实现)
  - [2.3 算法性能分析](#2.3 算法性能分析)
  - [2.4 小结](#2.4 小结)
- [3. 交换排序](#3. 交换排序)
- - [3.1 冒泡排序](#3.1 冒泡排序)
  - - [3.1.1 过程](#3.1.1 过程)
    - - [3.1.1.1 第一趟](#3.1.1.1 第一趟)
      - [3.1.1.2 第二趟](#3.1.1.2 第二趟)
      - [3.1.1.3 第三趟](#3.1.1.3 第三趟)
      - [3.1.1.4 第四趟](#3.1.1.4 第四趟)
      - [3.1.1.5 第五趟](#3.1.1.5 第五趟)
    - [3.1.2 算法实现](#3.1.2 算法实现)
    - [3.1.3 算法性能分析](#3.1.3 算法性能分析)
    - [3.1.4 小结](#3.1.4 小结)
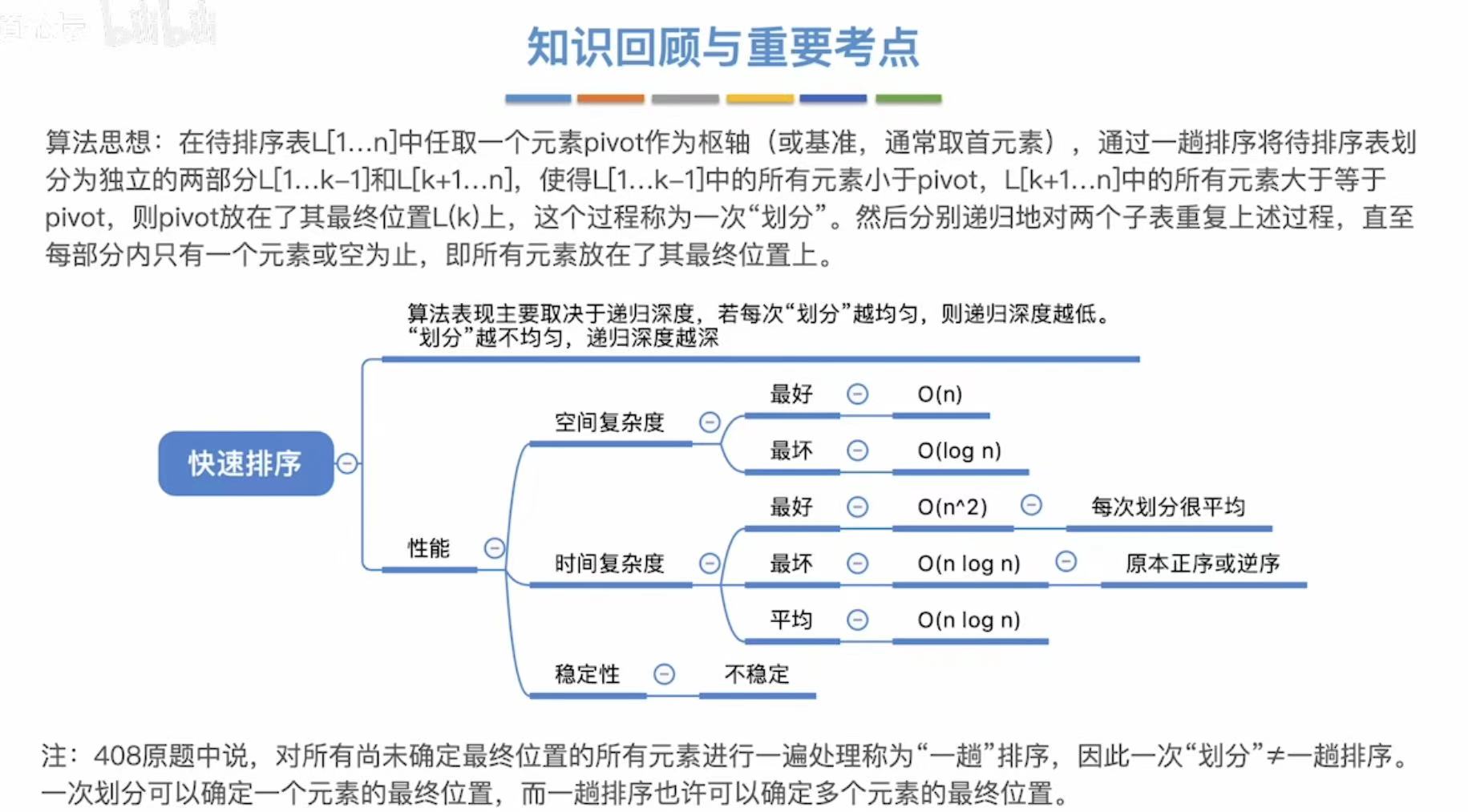
  - [3.2 快速排序](#3.2 快速排序)
  - - [3.2.1 算法思想](#3.2.1 算法思想)
    - [3.2.2 算法实现](#3.2.2 算法实现)
    - [3.2.3 算法效率分析](#3.2.3 算法效率分析)
    - [3.2.4 小结](#3.2.4 小结)

排序

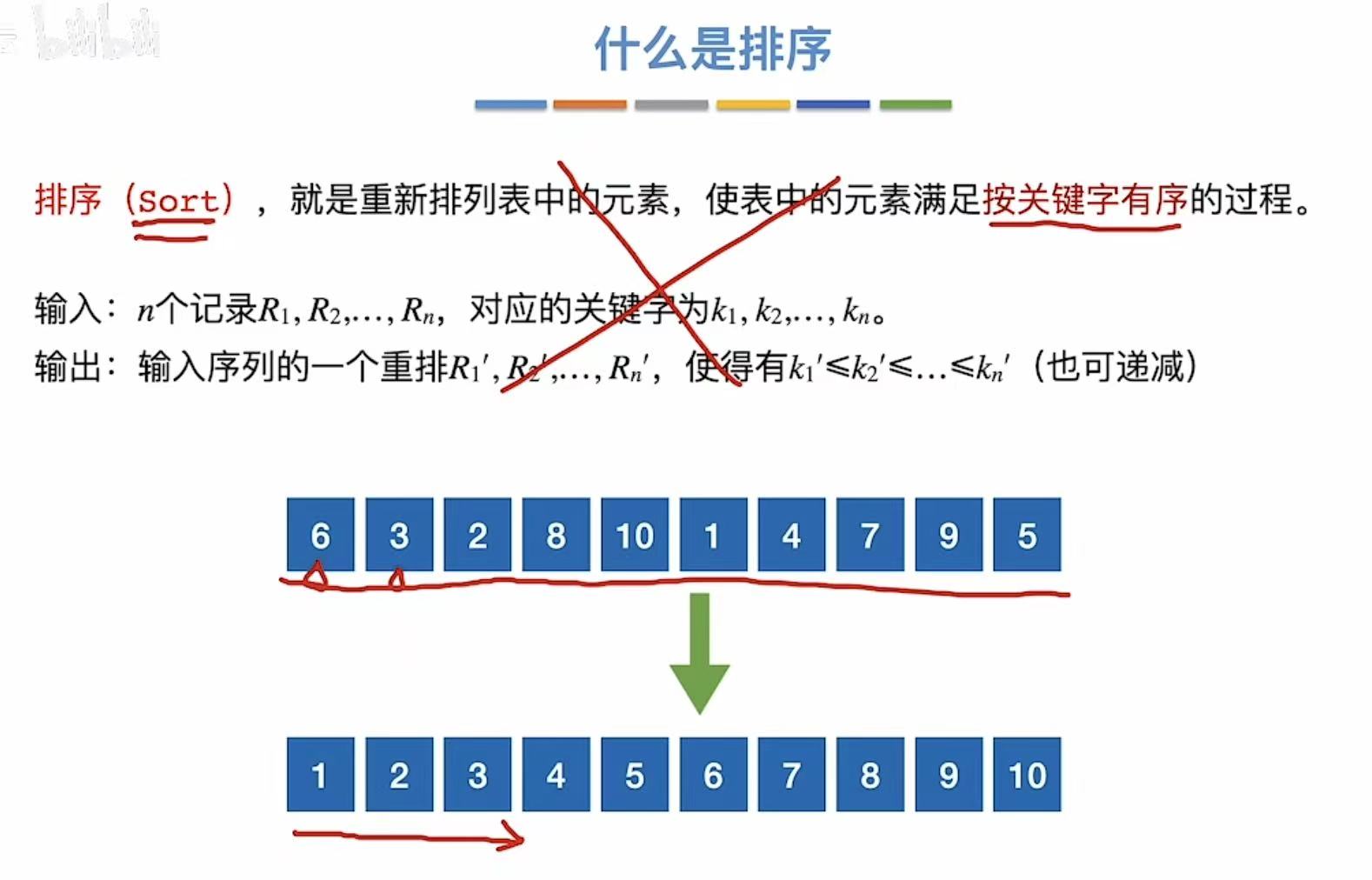
1. 什么是排序

就是把一串乱糟糟的数据，从小到大/从大到小有序排列。

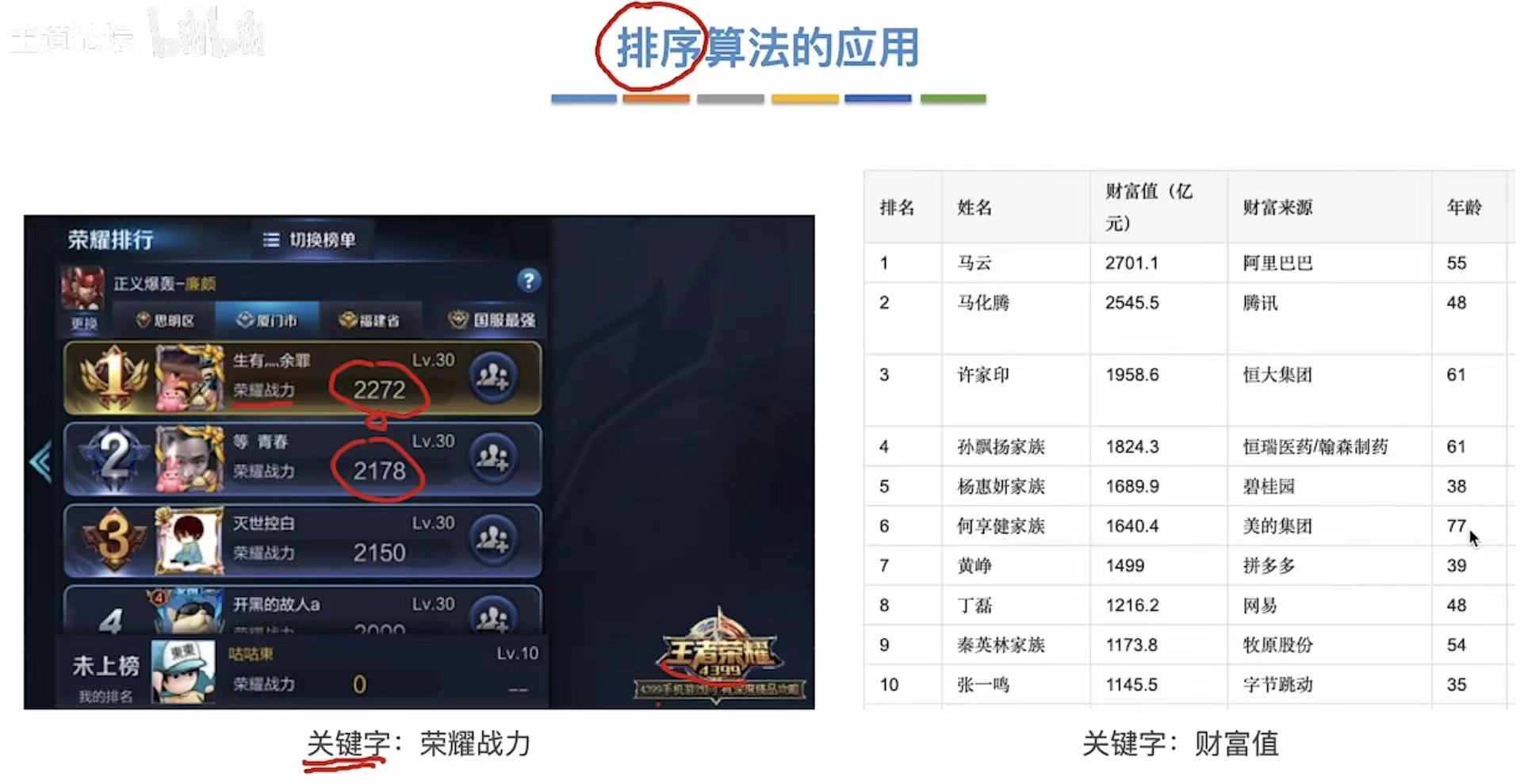
2. 排序算法的应用

3. 排序算法的评价指标

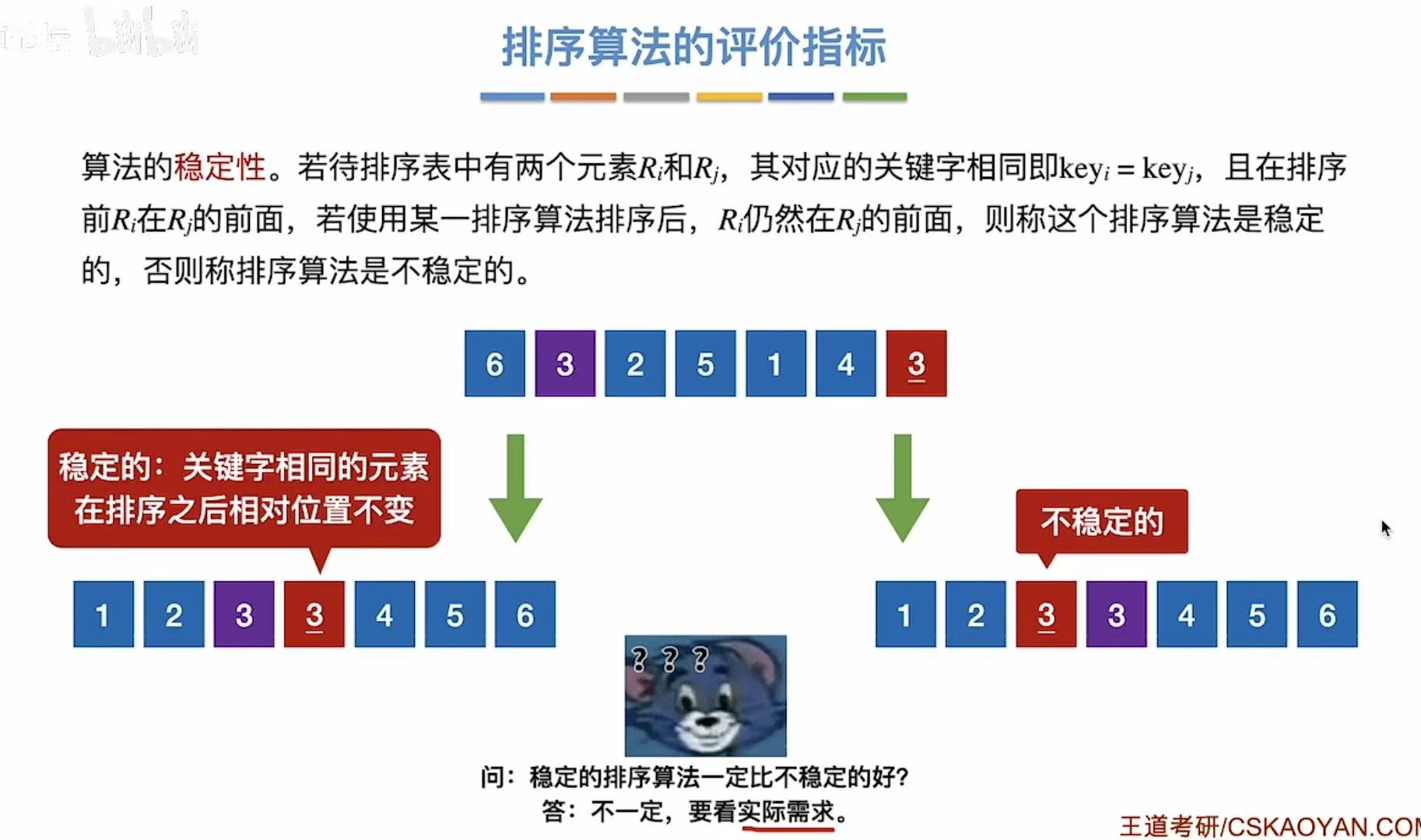
时间复杂度、空间复杂度和稳定性。

稳定：两个相同的数，没排序之前A左B右，排了之后依旧A左B右。
不稳定 ：两个相同的数，没排序之前A左B右，排了之后变A右B左。

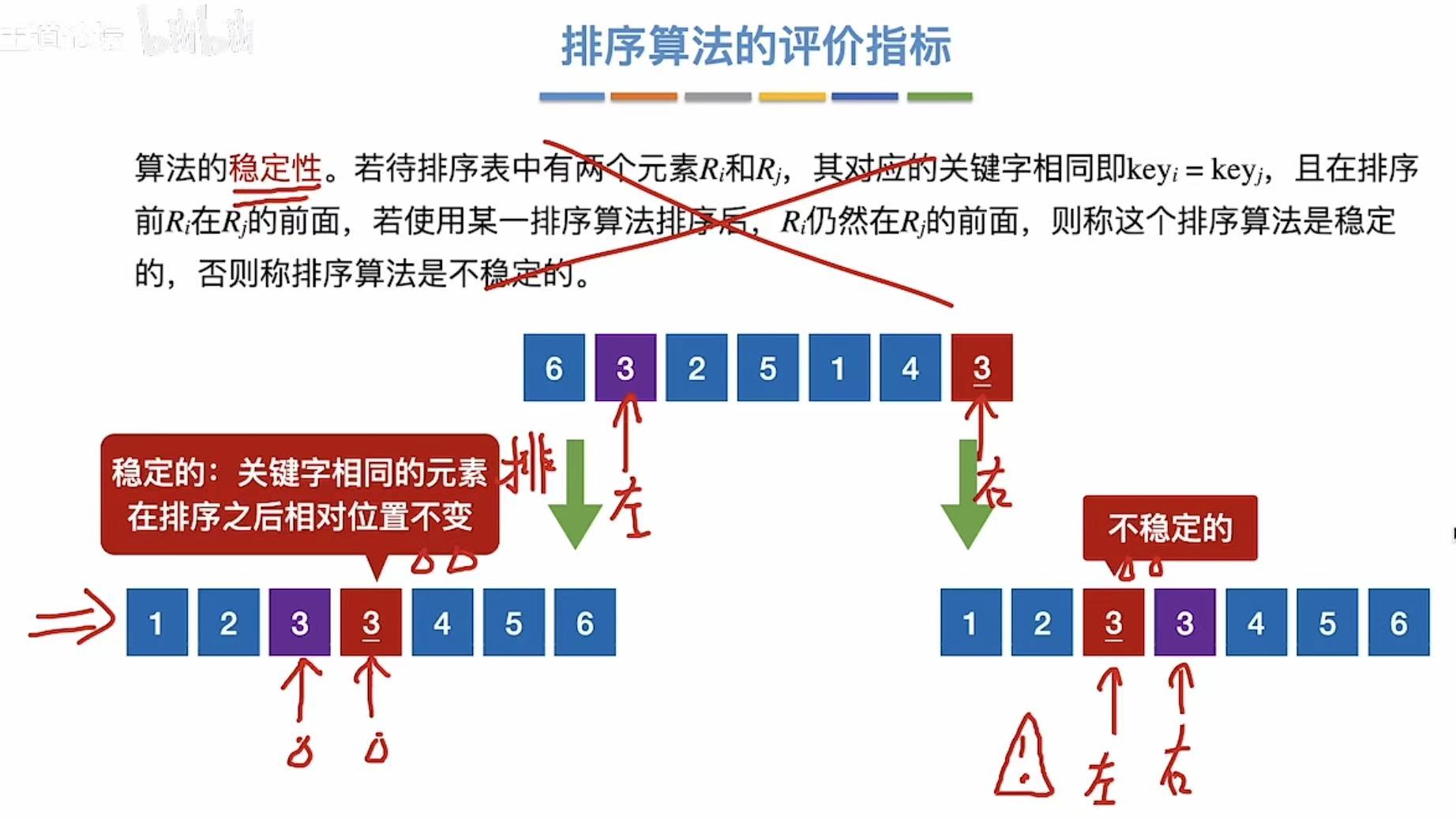
不一定稳定的就是最好的，还是一个场景一个判断，看具体需求，合适的才是最好的。

4. 排序算法的分类

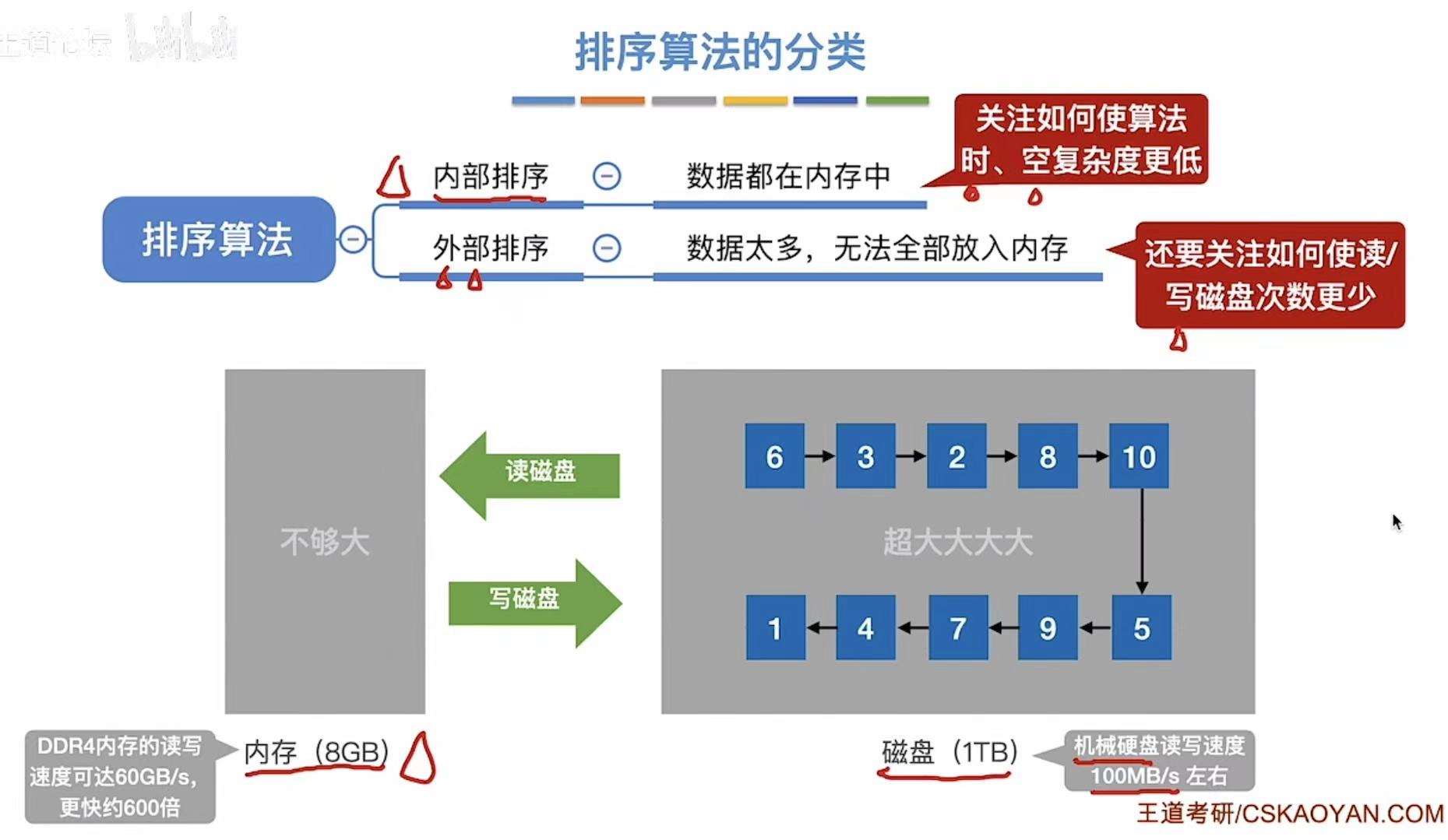
排序分为内部排序 和外部排序，我们主要学习的是内部排序。

内部排序：内存、时间复杂度和空间复杂度。
外部排序 ：外存、也就是磁盘，所以要关注怎么才能让磁盘读写次数降低。

5. 小结

内部排序

1. 插入排序

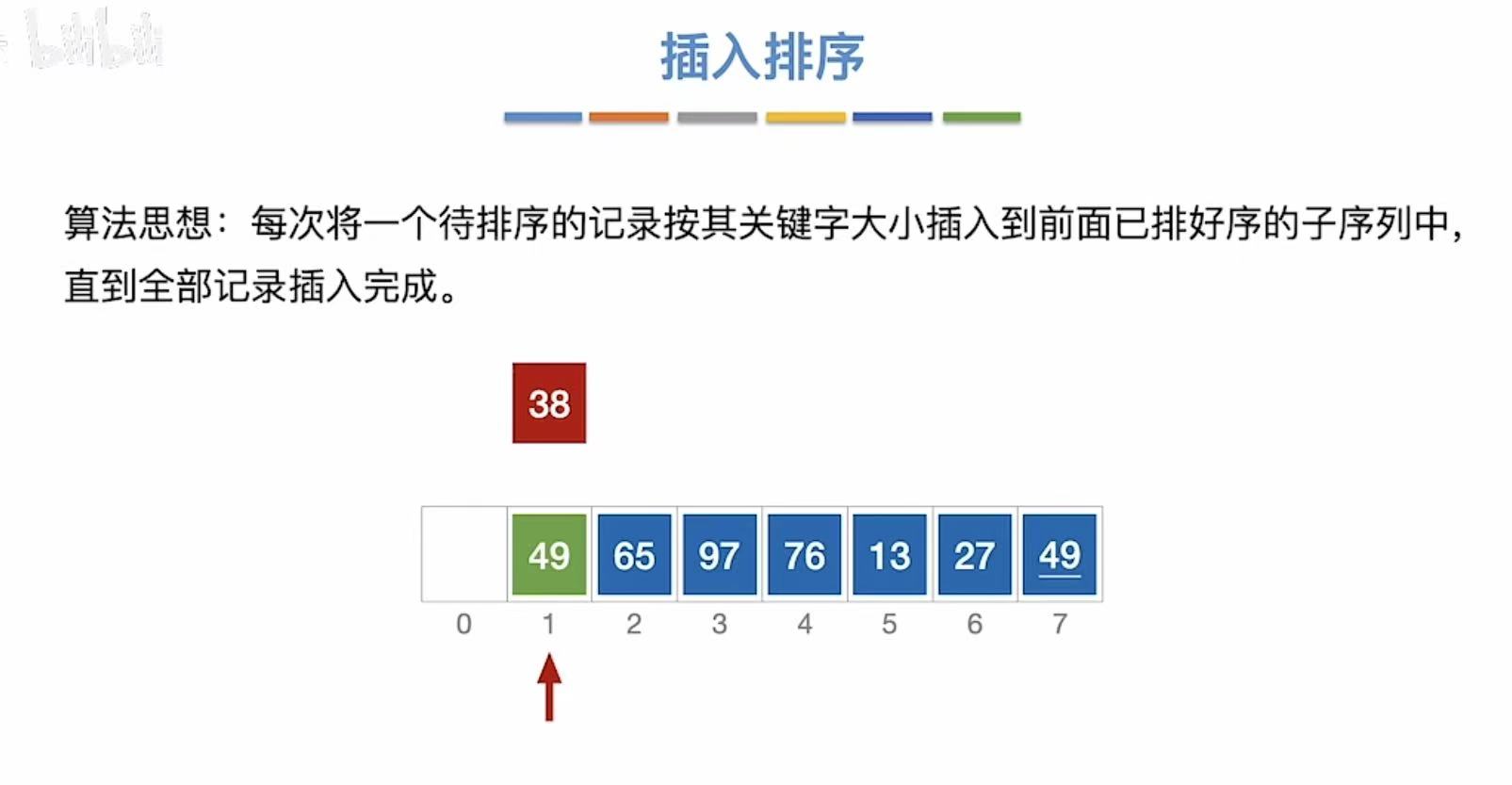
1.1 算法思想

待排序数列：

49和38比，49比38大，所以把38提出来，49移动到到38的位置，38插入49的位置
继续比对，65和97比，两个数的位置不变
97和76比，76出来，96移动到76原来的位置，然后76插入到96原来的位置
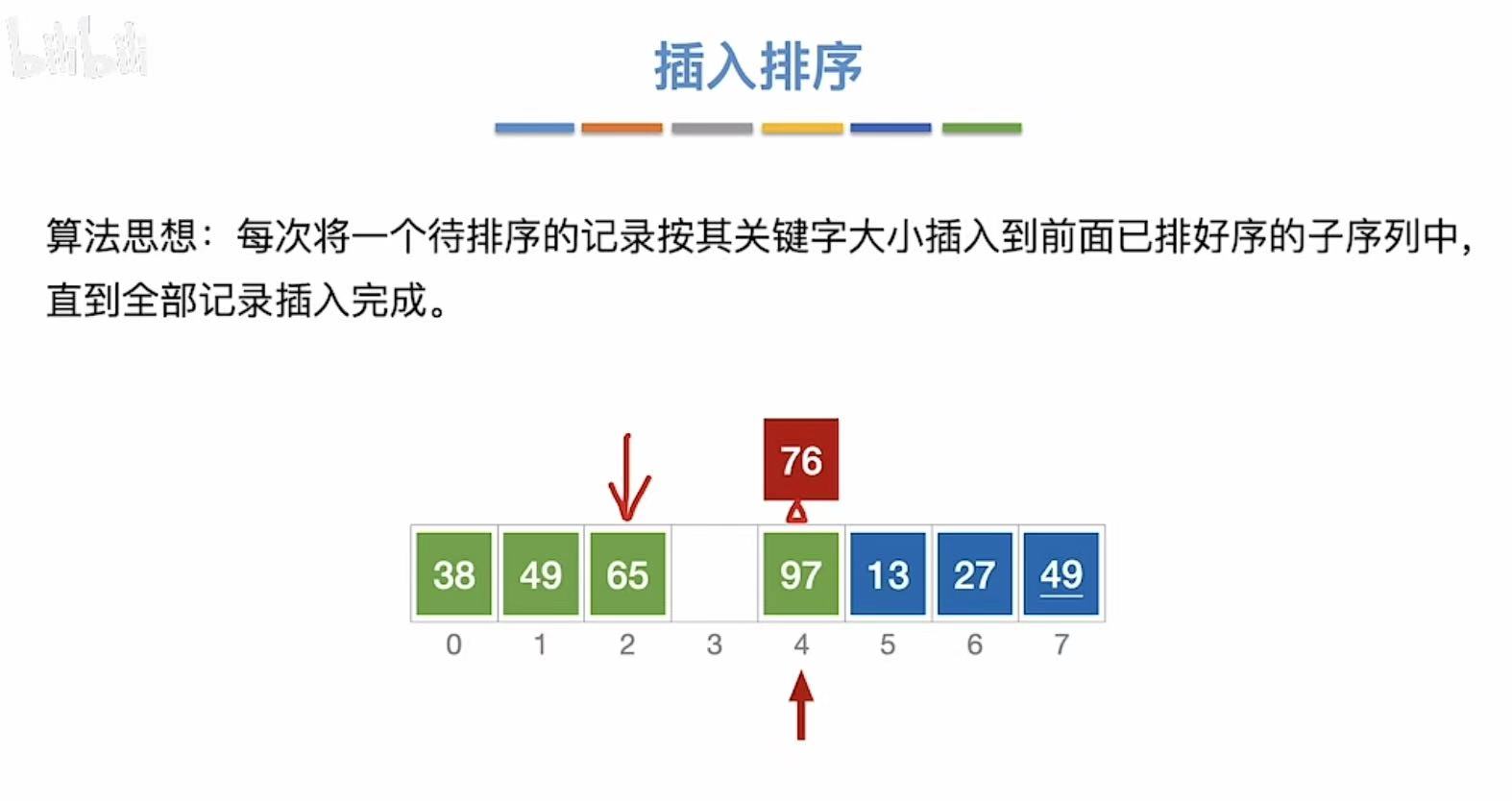
13和前面的所有数字比，13出来，前面所有数字向后移动一位，然后13插入到位置0
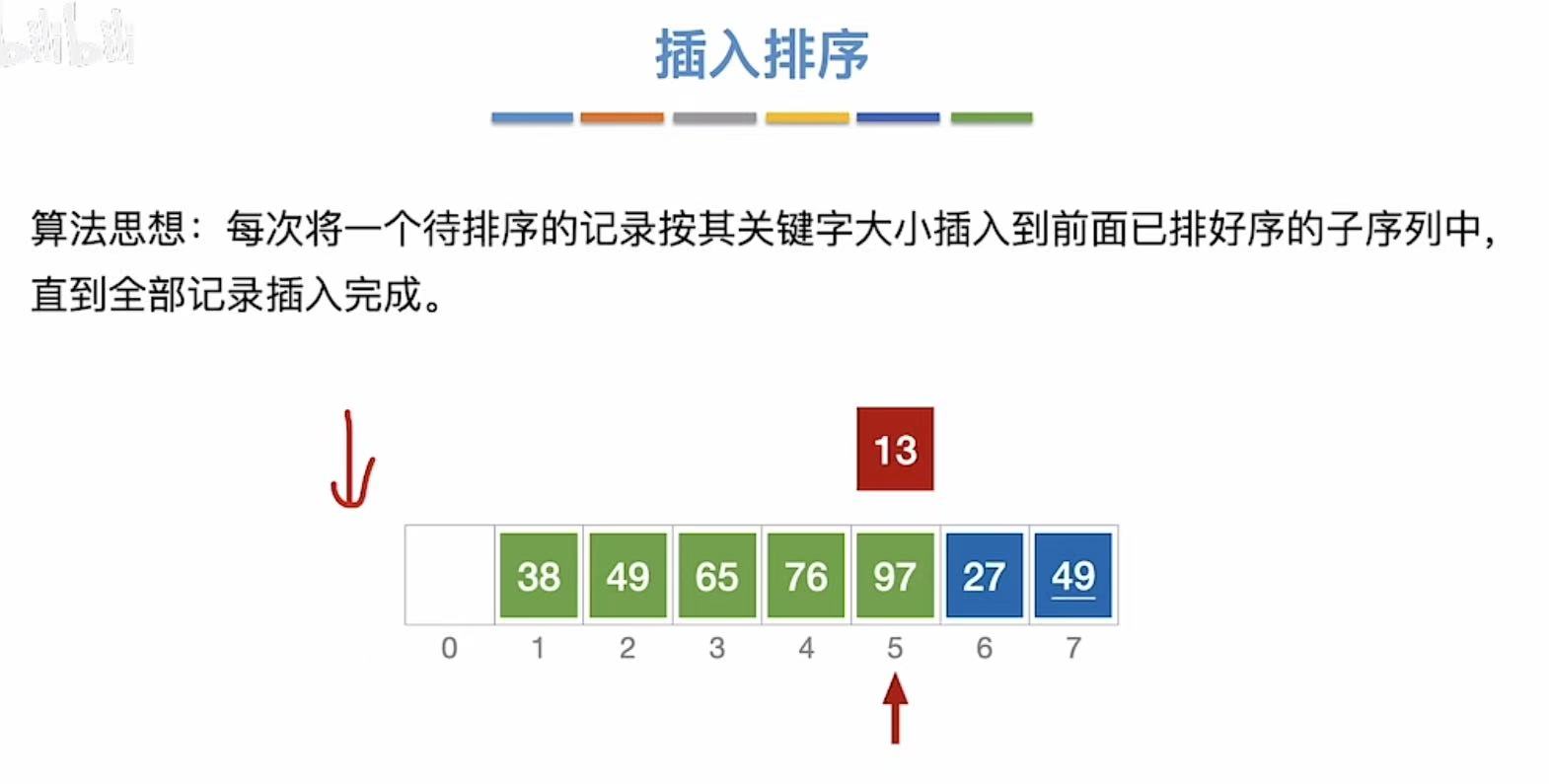
27和前面的所有数字比，27出来，前面除了13所有数字向后移动一位，然后27插入到位置1
49和前面的所有数字比，49出来，因为和第一个49相等，所以插入到第一个49的位置的后面

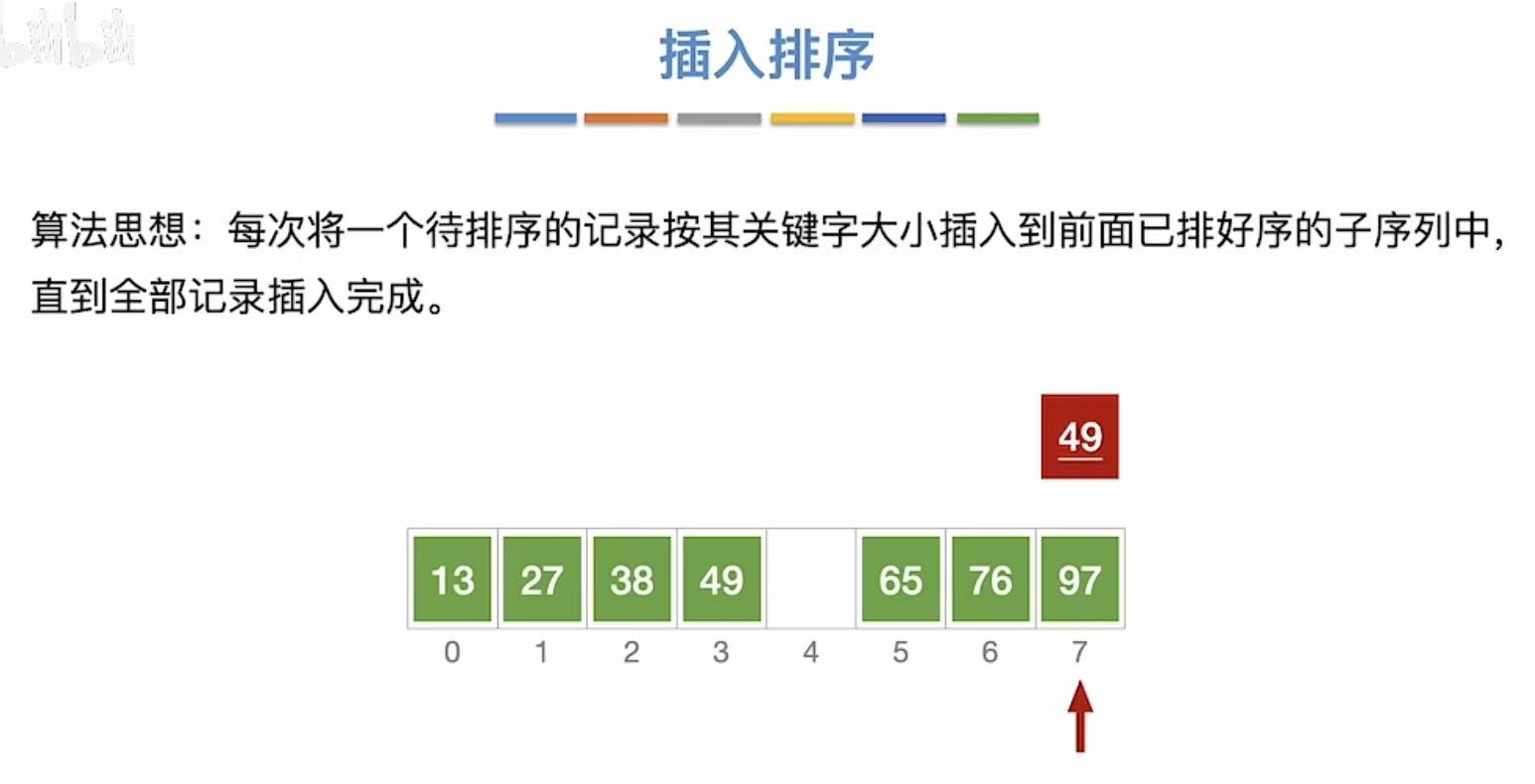
1.2 算法实现

java 复制代码

// 直接插入排序：将数组 A 的每个元素依次插入到前面已排好序的部分中
void InsertSort(int A[], int n) {
    int i, j, temp;           // i: 当前待插入元素的下标；j: 用于向前比较的指针；temp: 暂存当前元素

    // 外层循环：从第二个元素（i=1）开始，依次处理每个元素
    for (i = 1; i < n; i++) { 
        // 如果当前元素 A[i] 小于前一个元素 A[i-1]，说明需要插入调整
        if (A[i] < A[i-1]) {
            // 用 temp 临时保存当前要插入的元素 A[i]
            temp = A[i];

            // 内层循环：从 i-1 开始，向前遍历已排序部分
            // 只要前面的元素大于 temp，就将其向后移动一位
            for (j = i - 1; j >= 0 && A[j] > temp; j--) {
                A[j + 1] = A[j];  // 将比 temp 大的元素向后挪一位
            }

            // 找到合适位置后，将 temp 插入到正确位置
            A[j + 1] = temp;
        }
    }
}

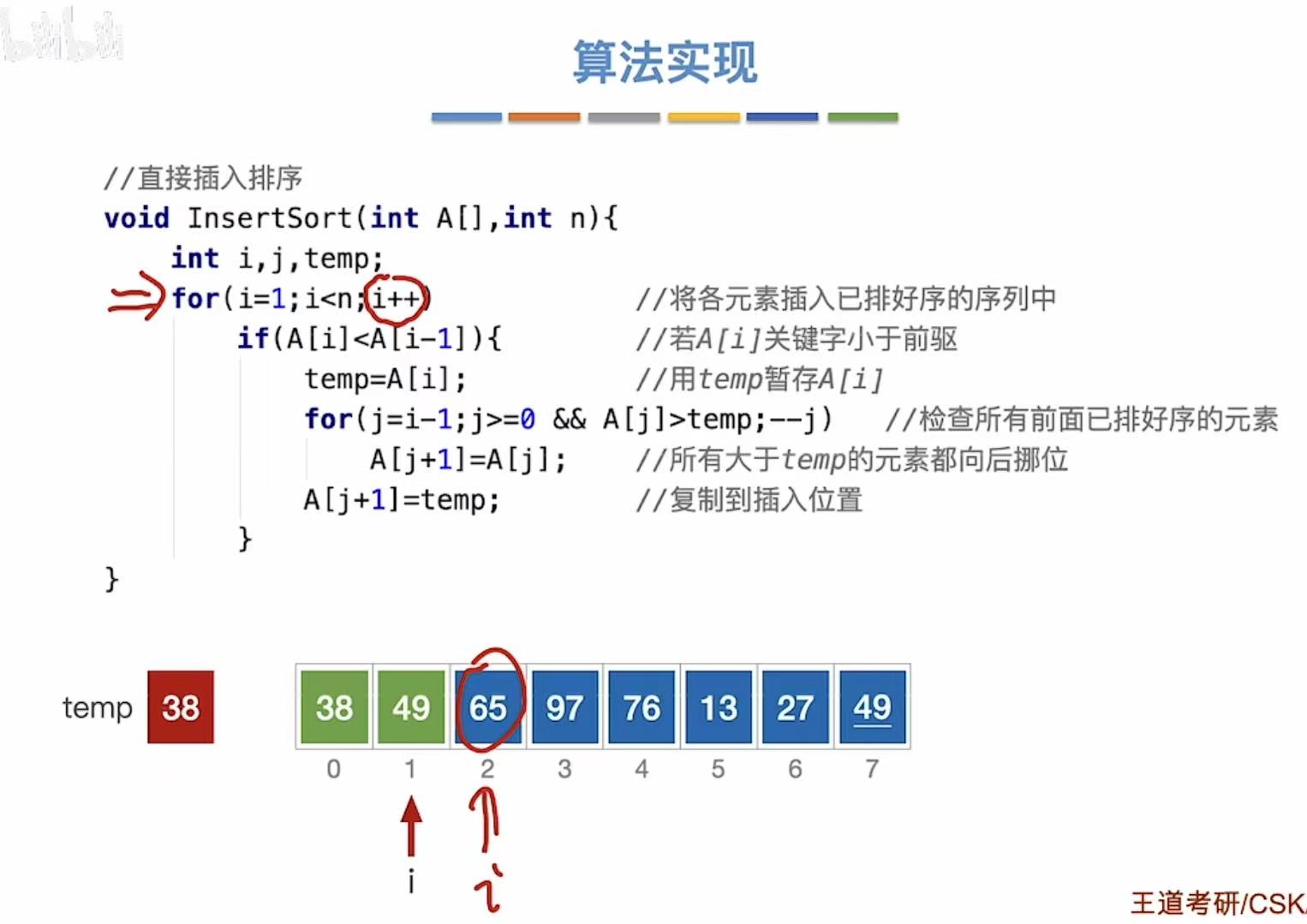
哨兵：就是位置0空出来专门放需要进行对比的数字
区别：上面的普通版是用temp存放需要比对的数字，哨兵是直接腾了个位置
优点：不用每轮循环都判断j>=0，因为当 j = 0 时，A[0] 正是待插入的值，比较会自然停止；

java 复制代码

// 直接插入排序（带哨兵）：通过设置"哨兵"避免每次循环判断 j >= 0
void InsertSort(int A[], int n) {
    int i, j;

    // 外层循环：从第二个元素（i=2）开始，依次处理每个元素
    // 注意：这里是从 i=2 开始，因为第一个元素（A[1]）已默认有序
    for (i = 2; i <= n; i++) { 
        // 如果当前元素 A[i] 小于前一个元素 A[i-1]，说明需要插入调整
        if (A[i] < A[i-1]) {
            // 将当前要插入的元素 A[i] 复制到 A[0]，作为"哨兵"
            // A[0] 不存放实际数据，仅用于简化比较条件
            A[0] = A[i]; 

            // 内层循环：从 i-1 开始，向前遍历已排序部分
            // 使用哨兵后，无需判断 j >= 0，因为 A[0] 已设为待插入值
            // 当 A[j] > A[0] 时，说明该元素大于待插入值，需向后移动
            for (j = i - 1; A[0] < A[j]; j--) {
                // 将比 A[0] 大的元素向后挪一位
                A[j + 1] = A[j];
            }

            // 找到合适位置后，将 A[0]（即原 A[i]）插入到正确位置
            A[j + 1] = A[0];
        }
    }
}

1.3 算法效率分析

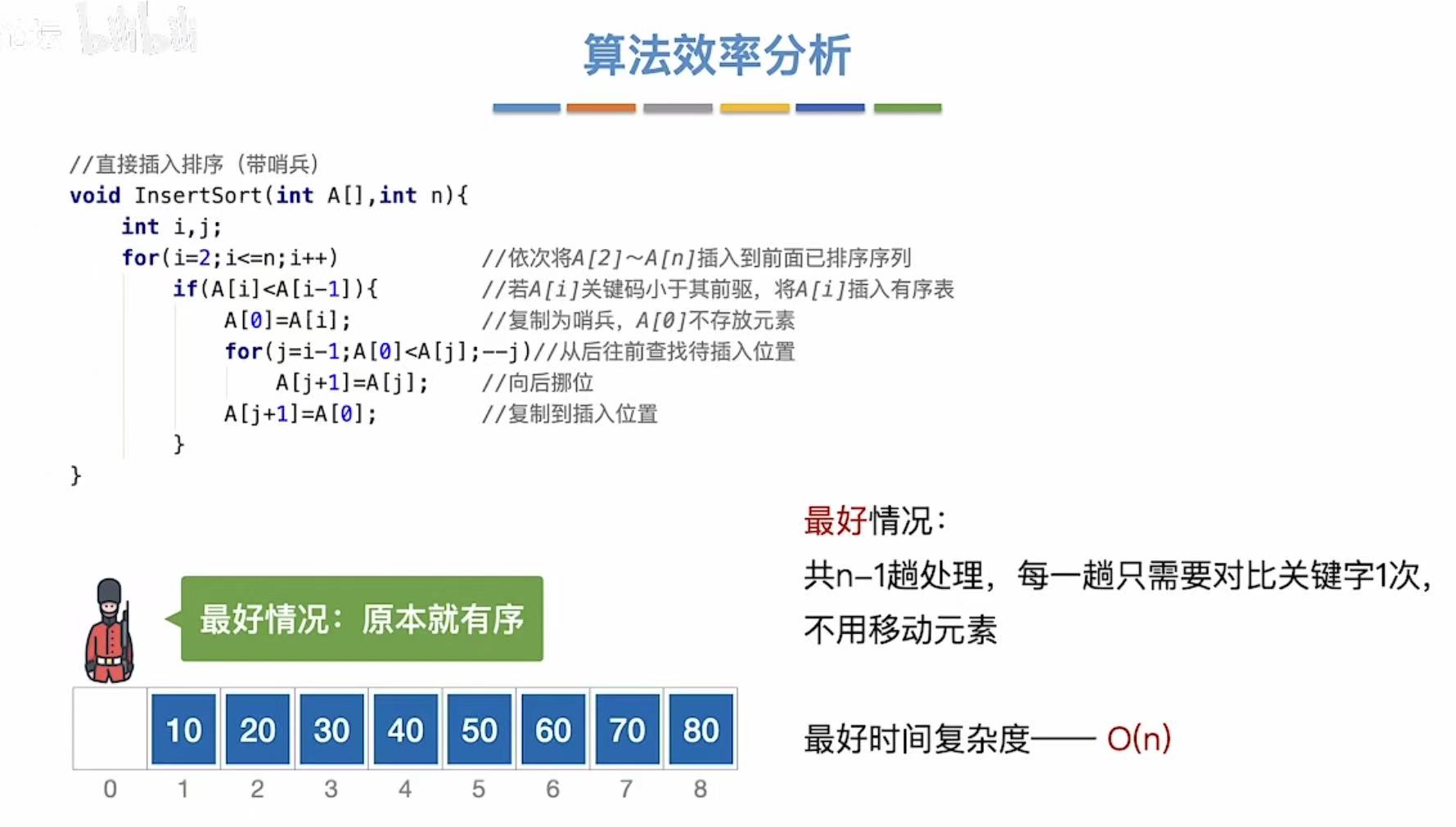
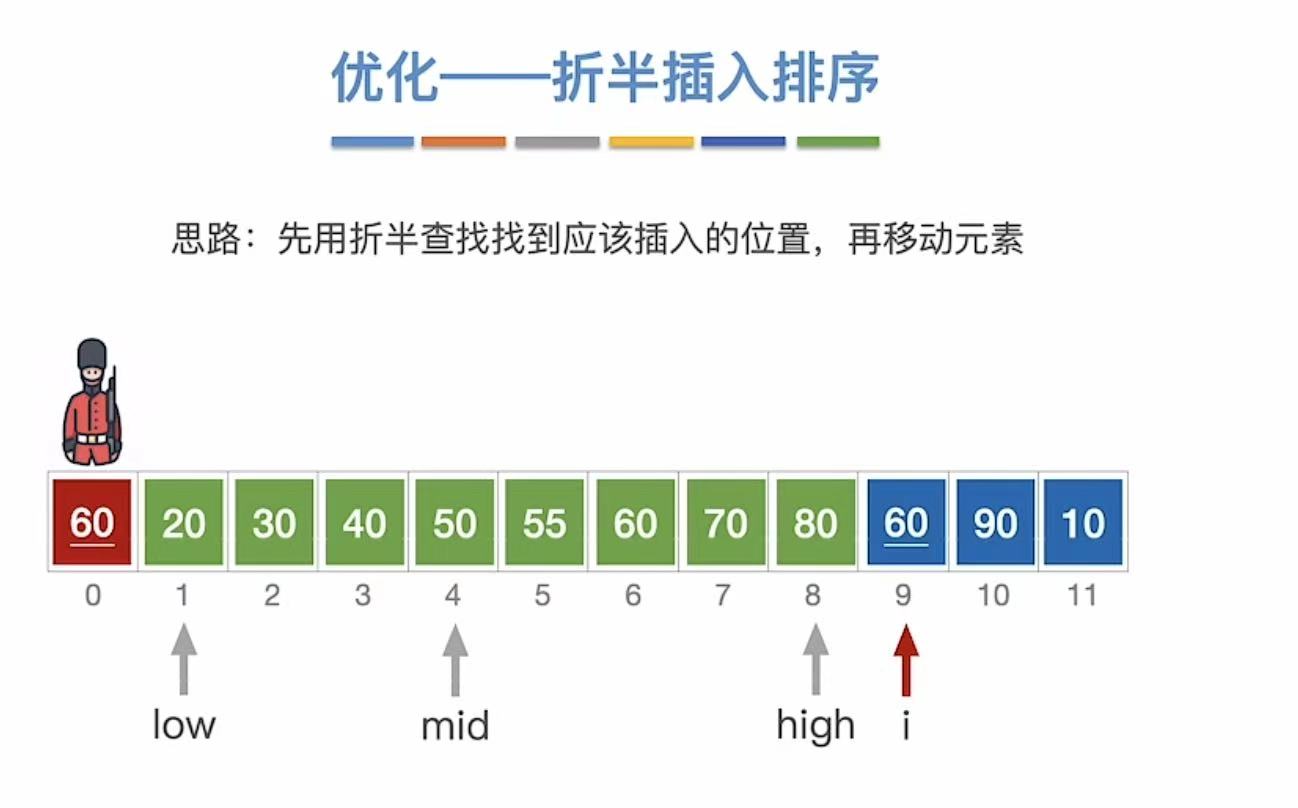
1.4 优化--折半插入排序

在寻找插入位置的时候用折半查找 。

折半查找具体可见：折半查找

1.4.1 第一次查找

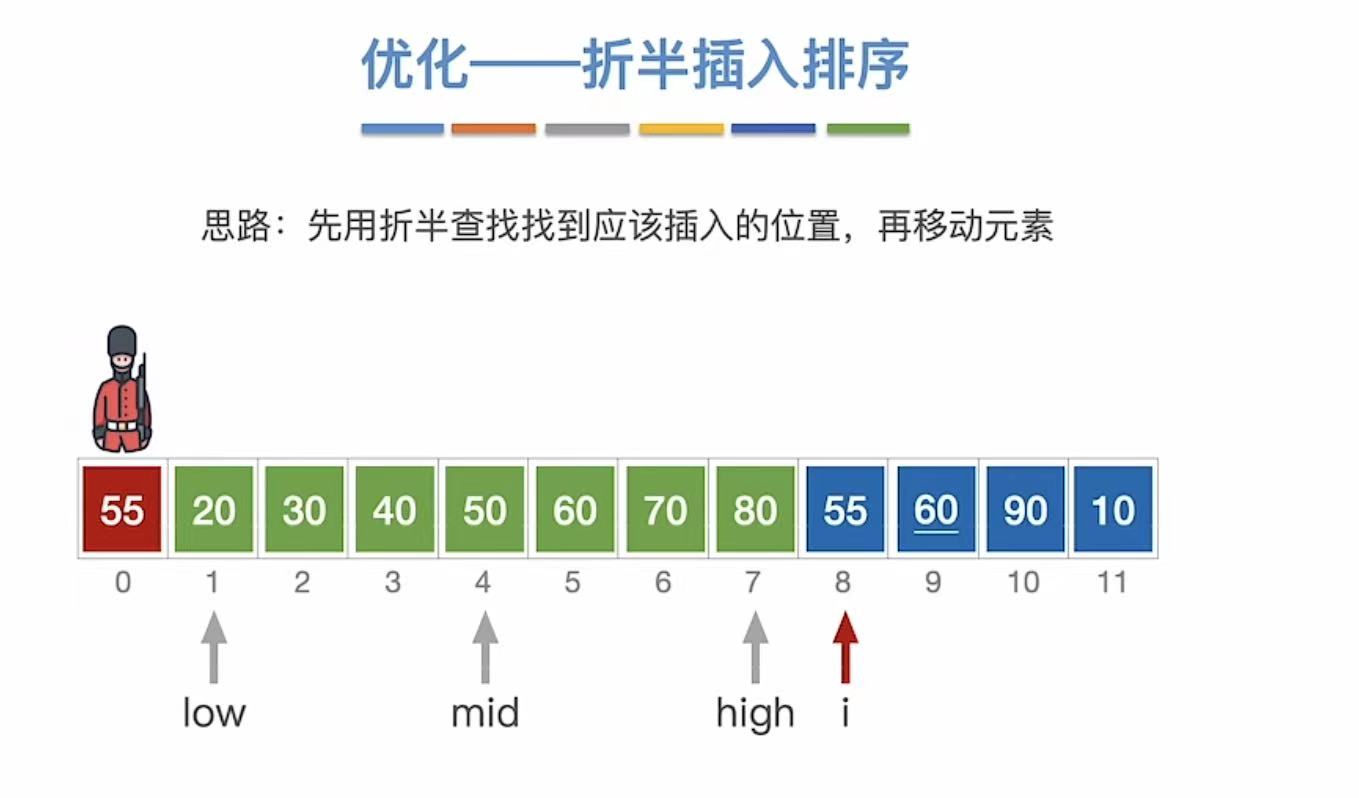
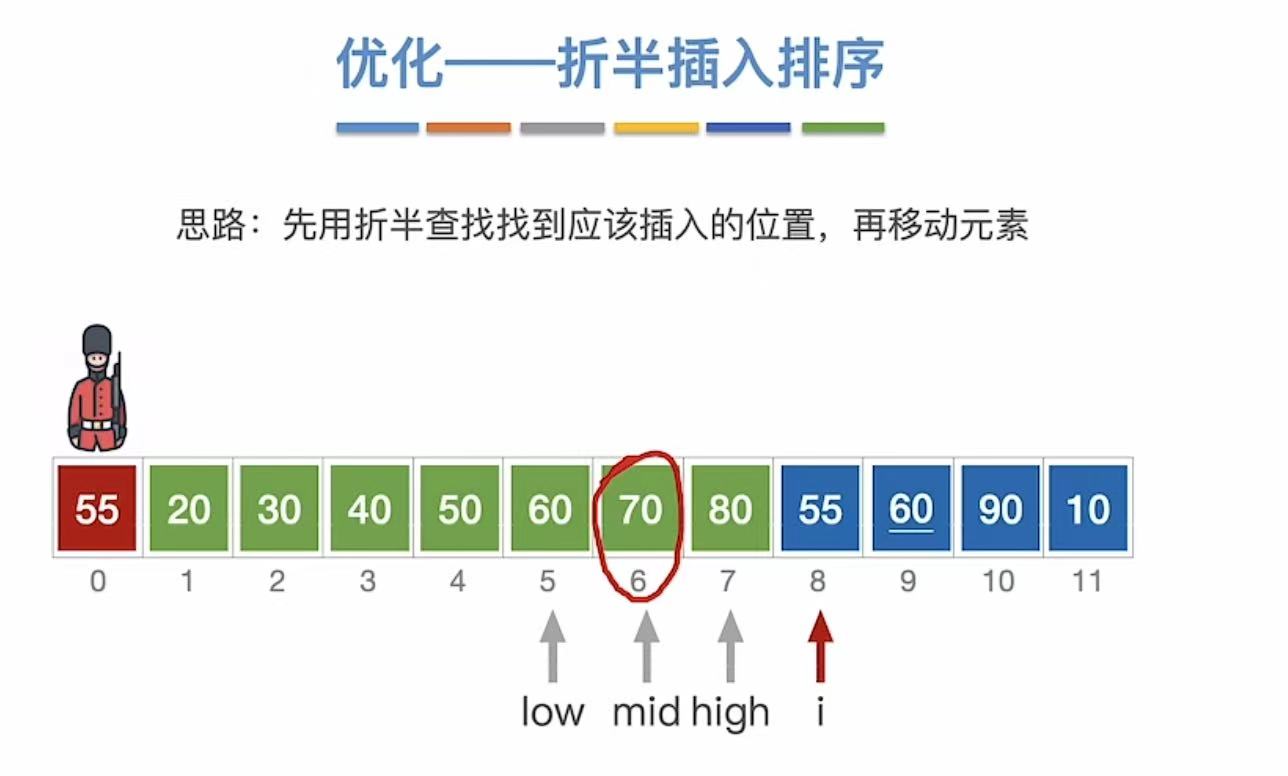
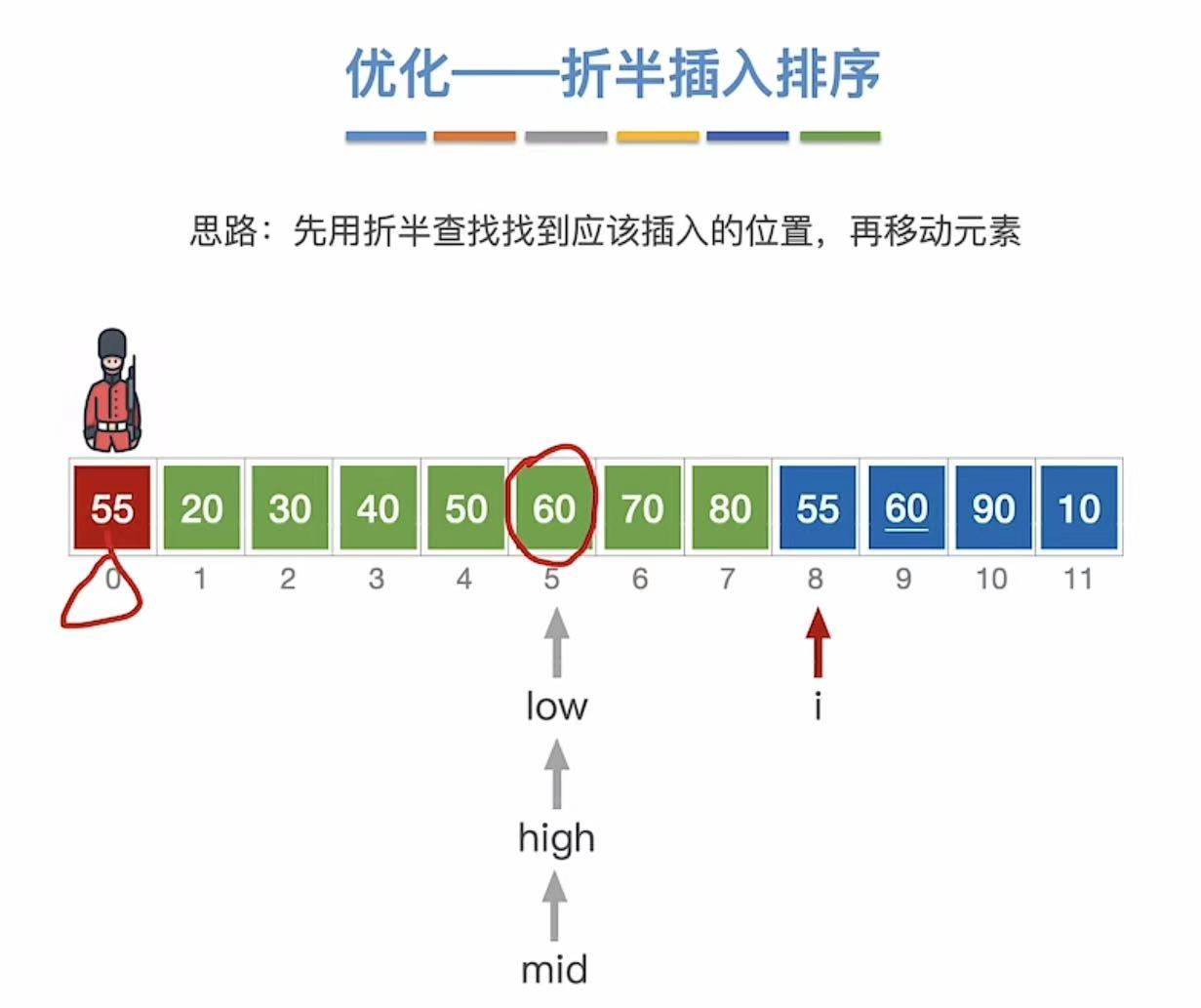
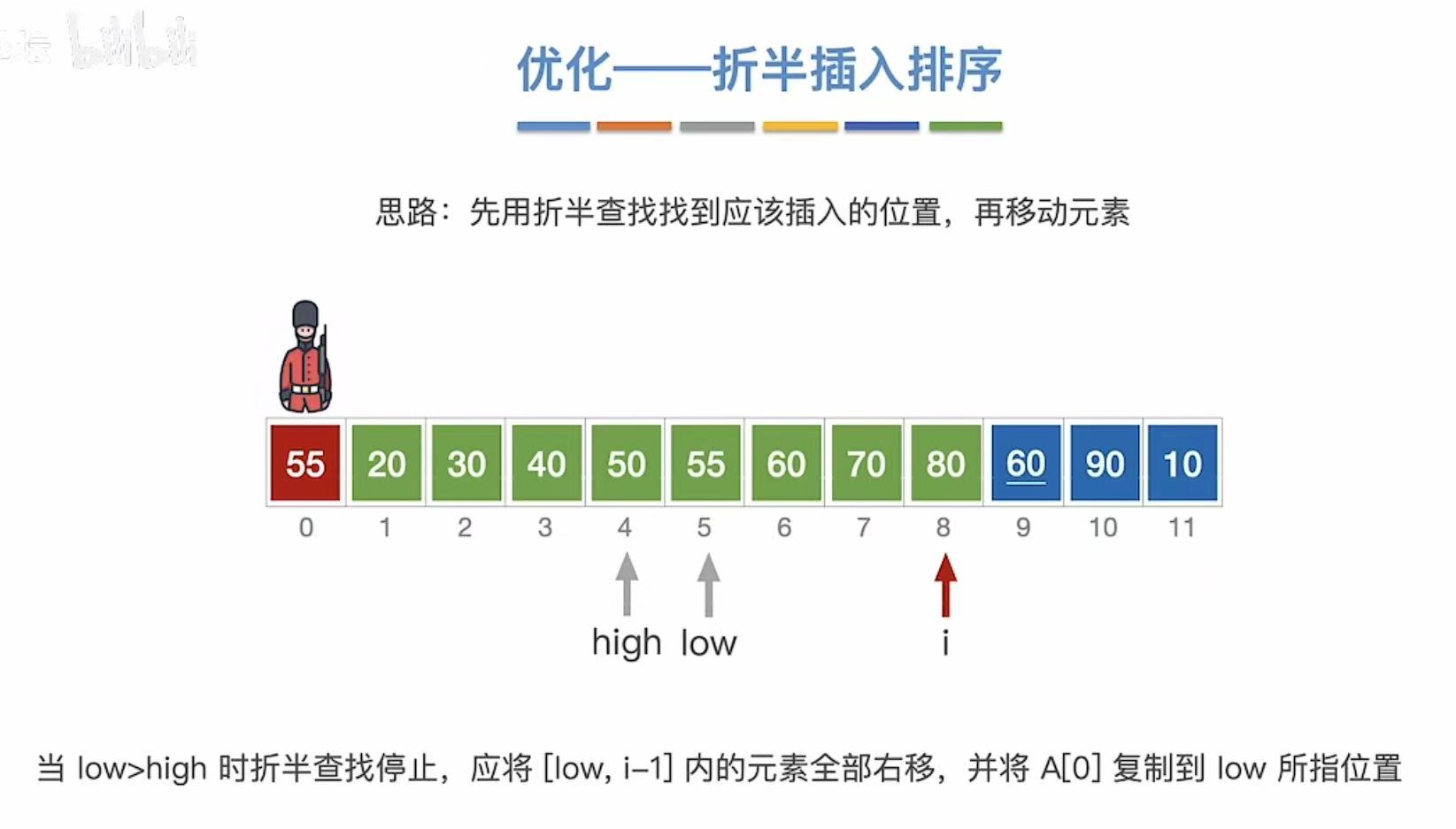
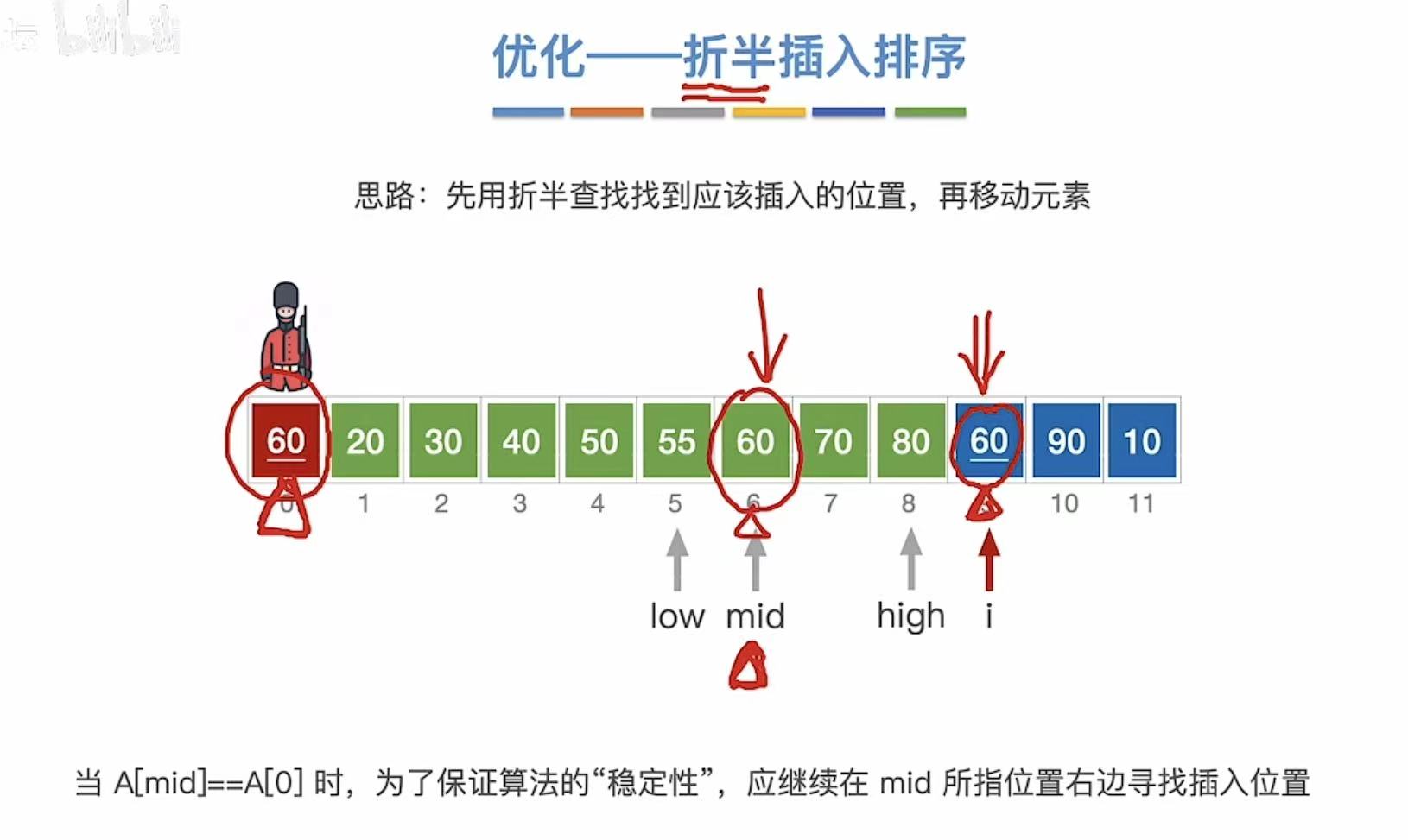
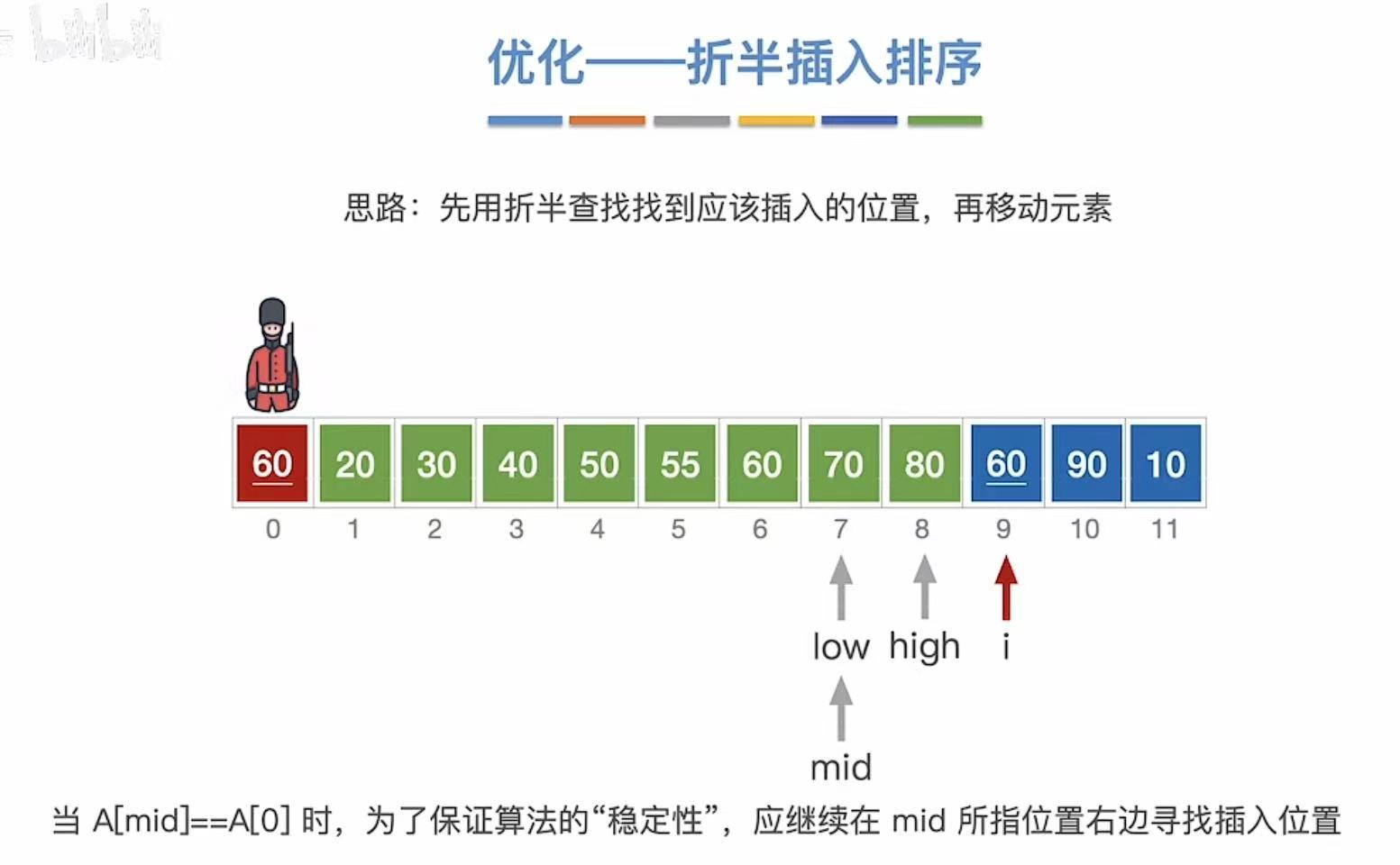
1.4.2 第二次查找

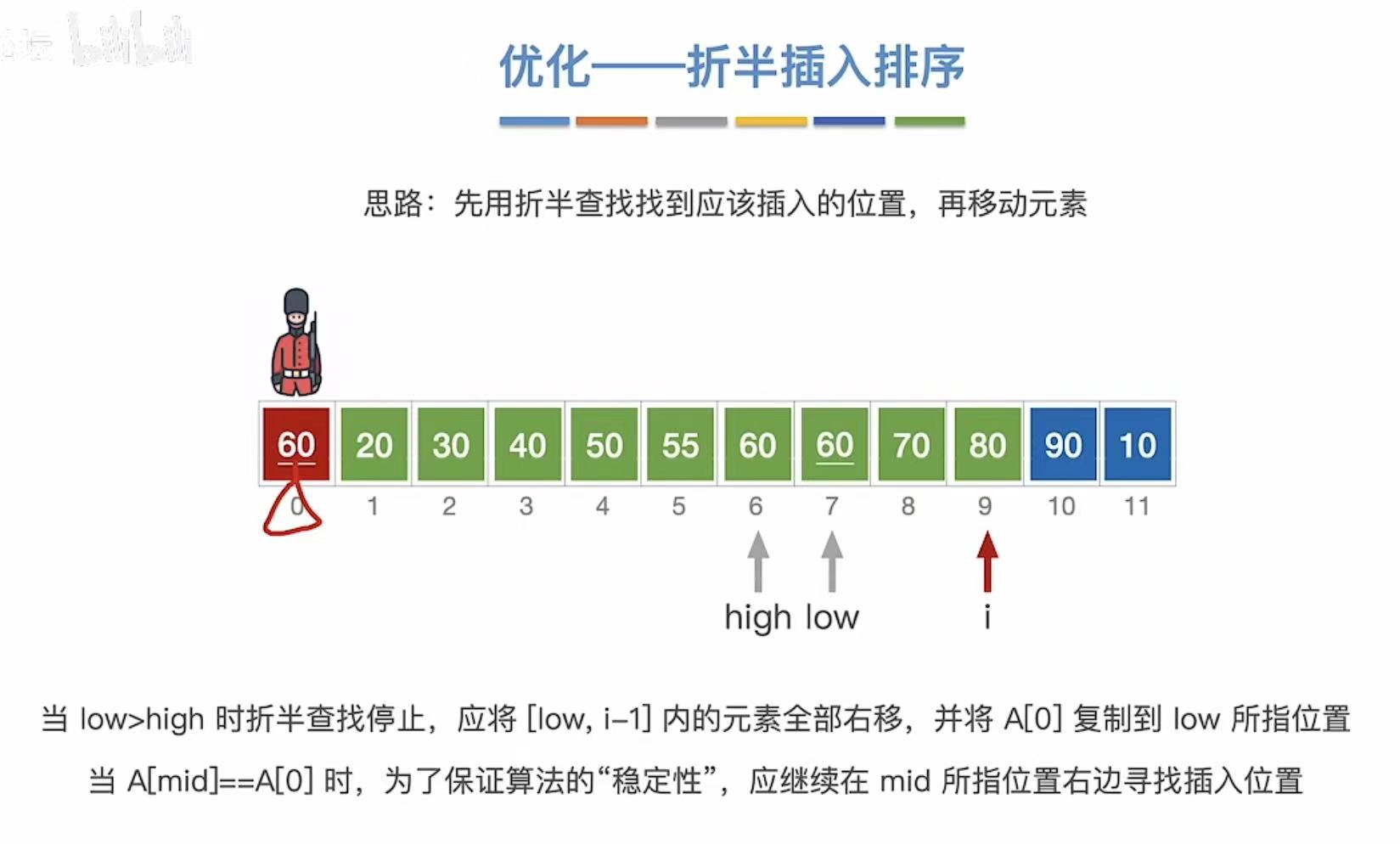
1.4.3 最终结果

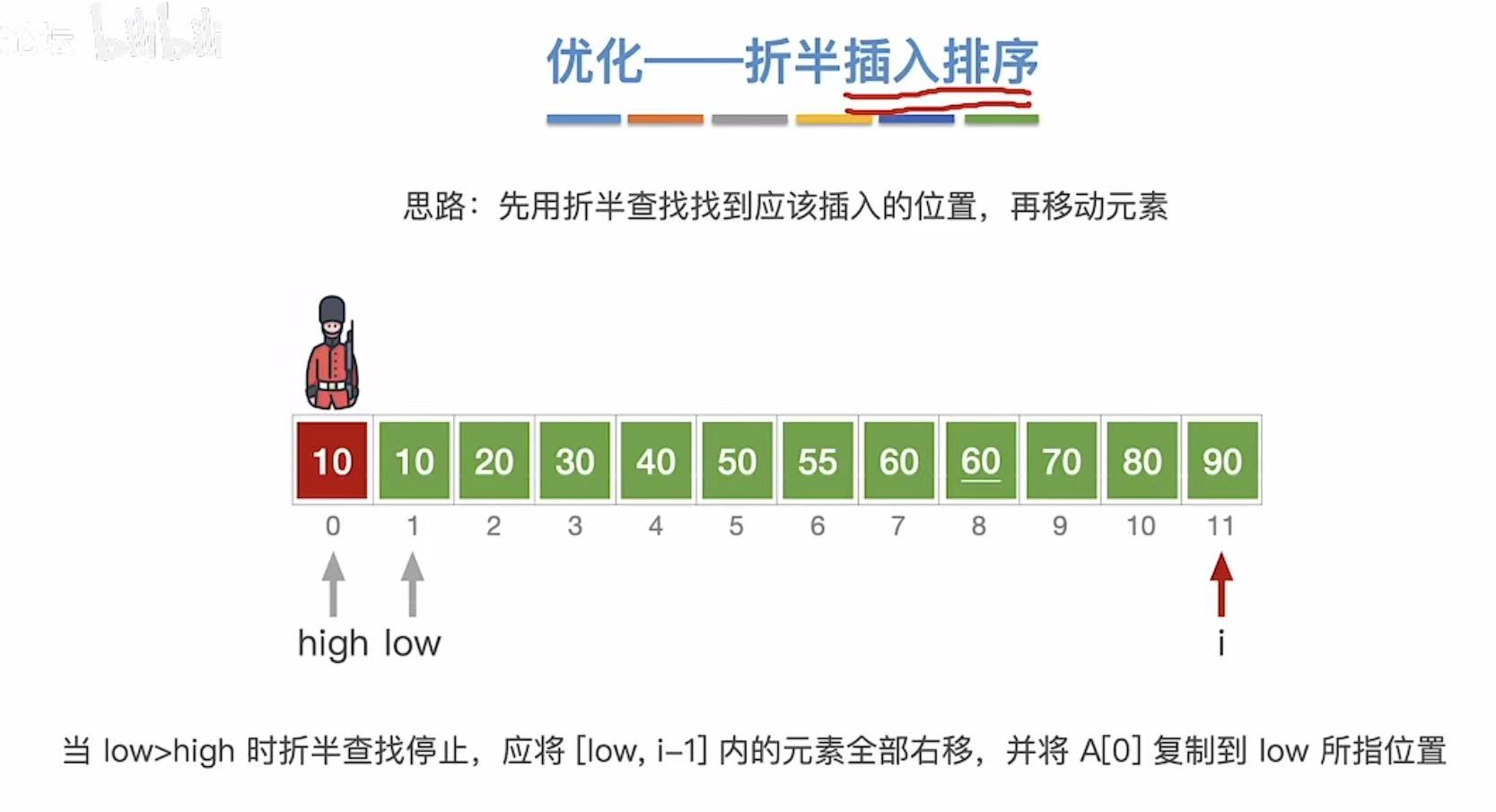
1.4.4 稳定&代码

稳定性：相同的数字依旧按照排序前的前后顺序。

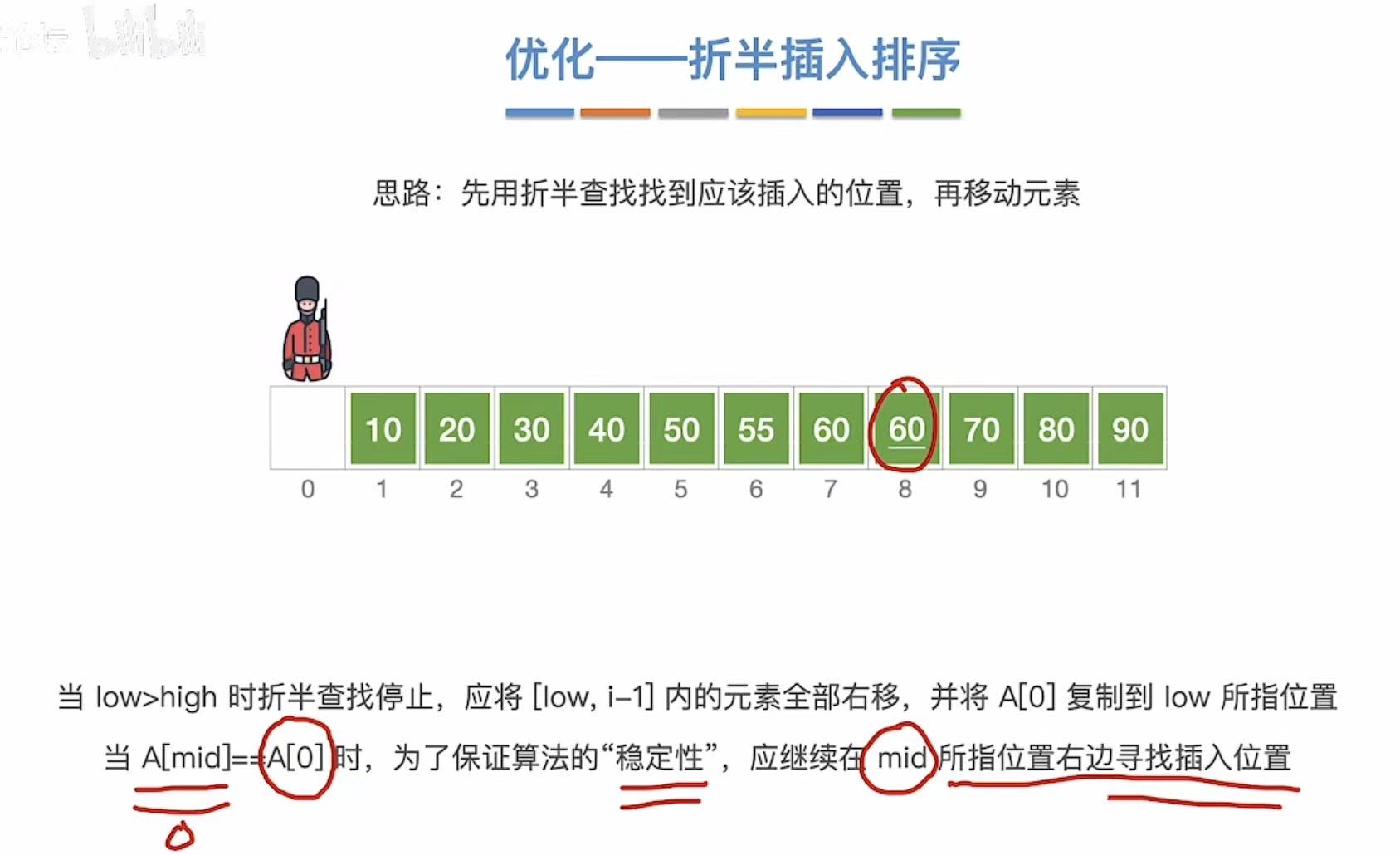
虽然但是，时间复杂度依旧没变。

java 复制代码

// 折半插入排序：在直接插入排序的基础上，用二分查找确定插入位置
void InsertSort(int A[], int n) {
    int i, j, low, high, mid;  // i: 当前待插入元素下标；j: 移动指针；low/high/mid: 二分查找范围

    // 外层循环：从第二个元素（i=2）开始，依次处理每个元素
    // 注意：这里是从 i=2 开始，因为第一个元素（A[1]）已默认有序
    for (i = 2; i <= n; i++) { 
        // 将当前要插入的元素 A[i] 复制到 A[0]，作为"哨兵"
        // A[0] 不存放实际数据，仅用于简化比较条件
        A[0] = A[i]; 

        // 设置二分查找的范围：[low, high]
        // 要在 [1, i-1] 区间中查找插入位置
        low = 1;
        high = i - 1;

        // 二分查找：找到 A[i] 应该插入的位置
        while (low <= high) {
            // 计算中间位置
            mid = (low + high) / 2;

            // 如果中间元素大于哨兵值，则说明插入位置在左半部分
            if (A[mid] > A[0]) {
                high = mid - 1;  // 缩小右边界
            } else {
                low = mid + 1;   // 缩小左边界
            }
        }

        // 此时 low 是插入位置，将 [low, i-1] 的元素全部向后移动一位
        // 为插入腾出空间
        for (j = i - 1; j >= low; j--) {
            A[j + 1] = A[j];
        }

        // 将哨兵值（即原 A[i]）插入到正确位置
        A[low] = A[0];
    }
}

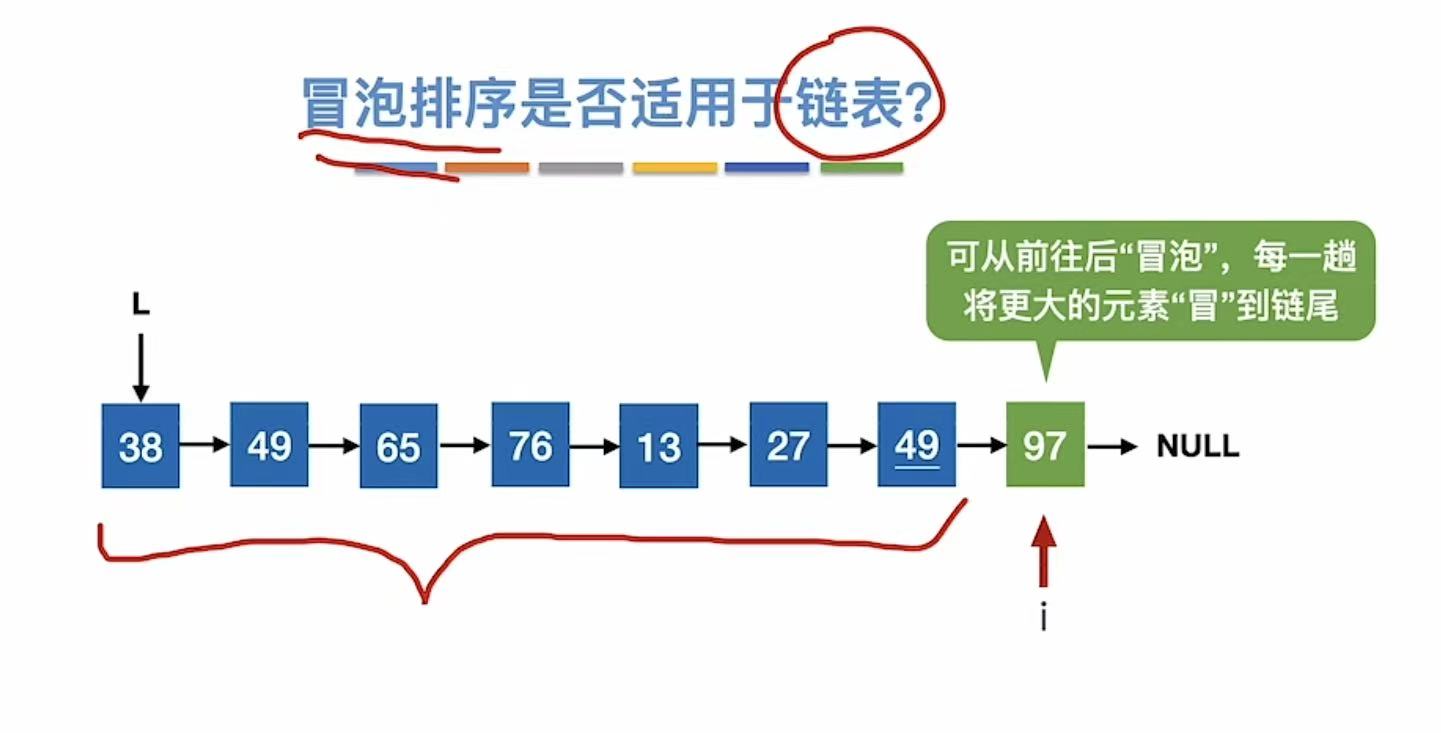
1.5 对链表进行插入排序

插入排序同样适用于链表。

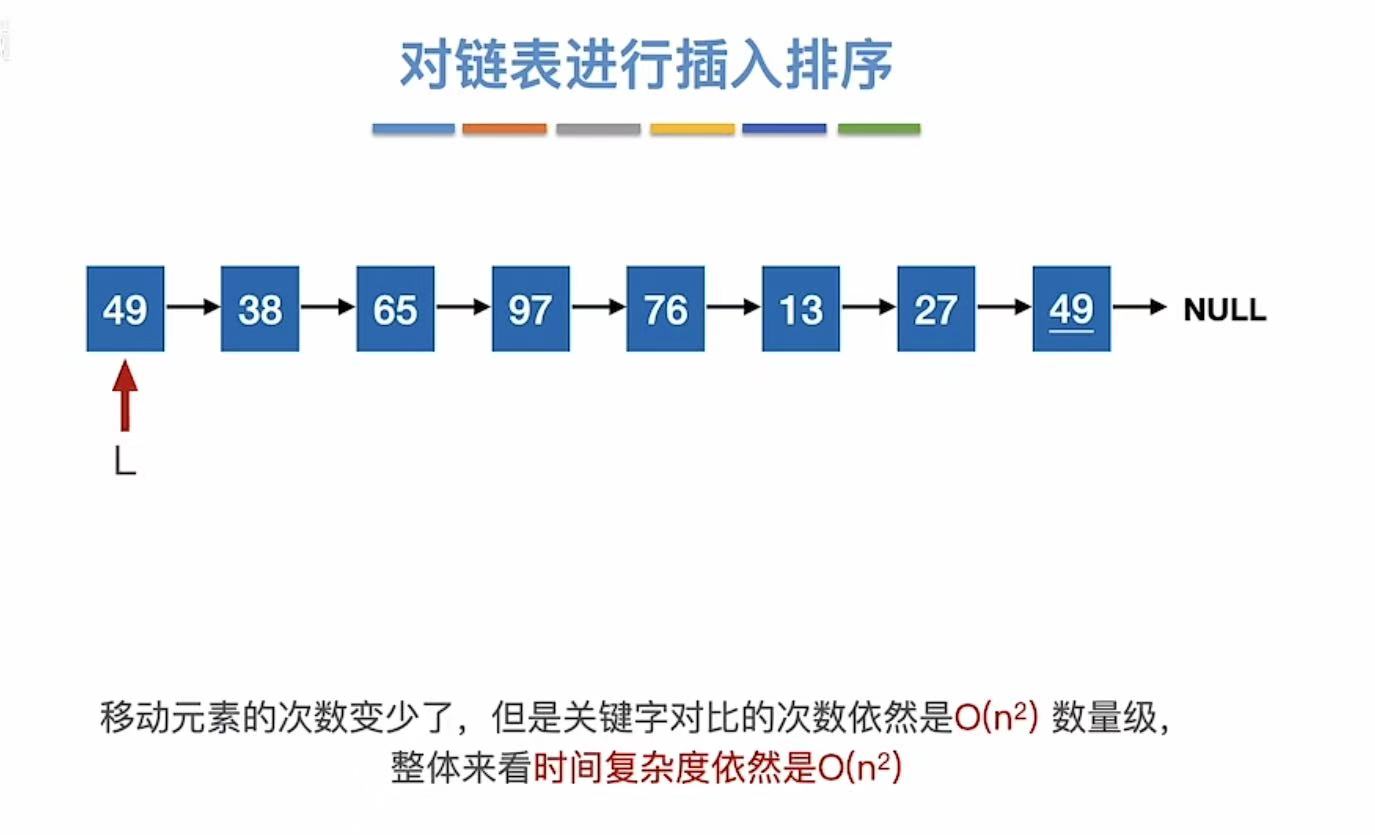
1.6 小结

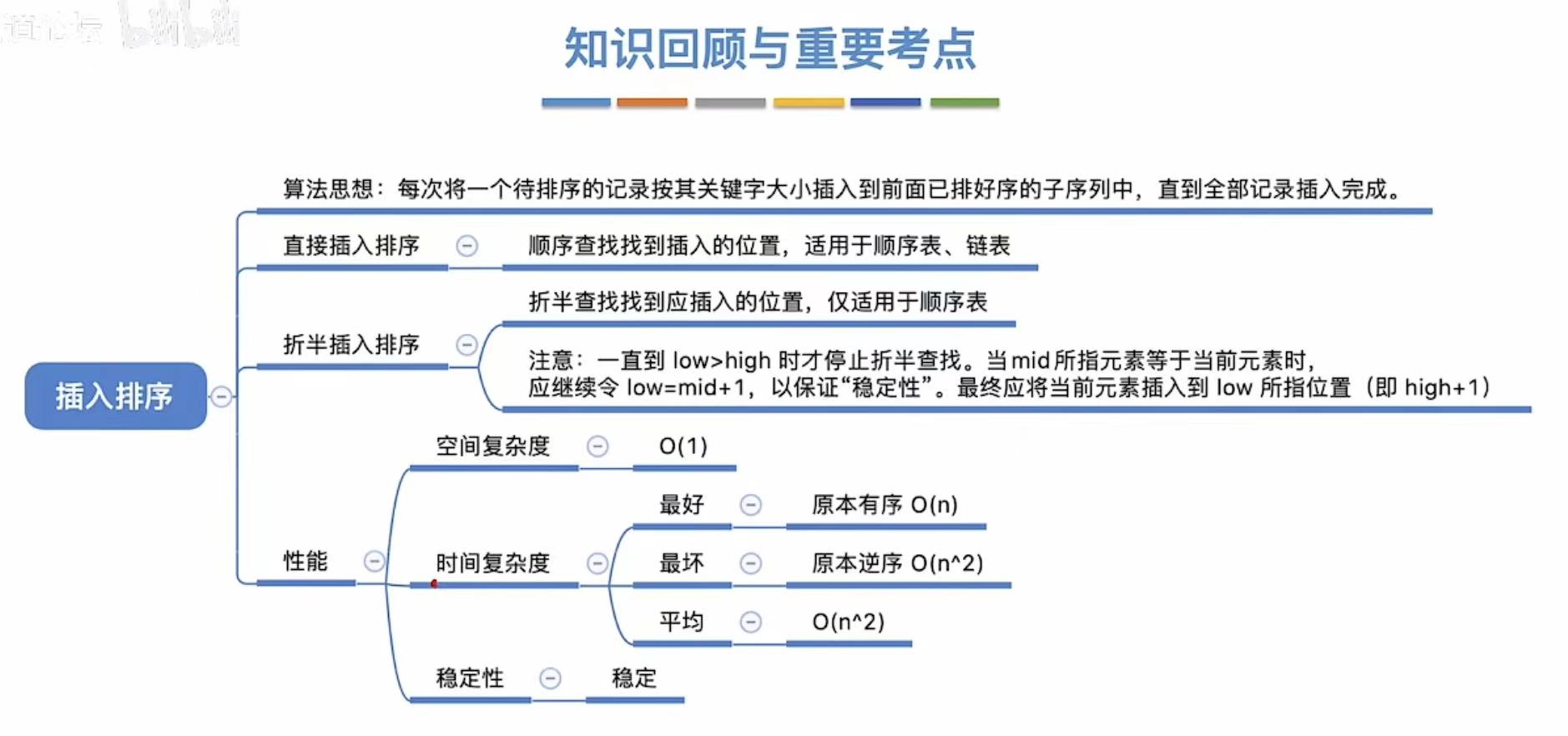
2. 希尔排序

混乱-->基本有序-->全局有序

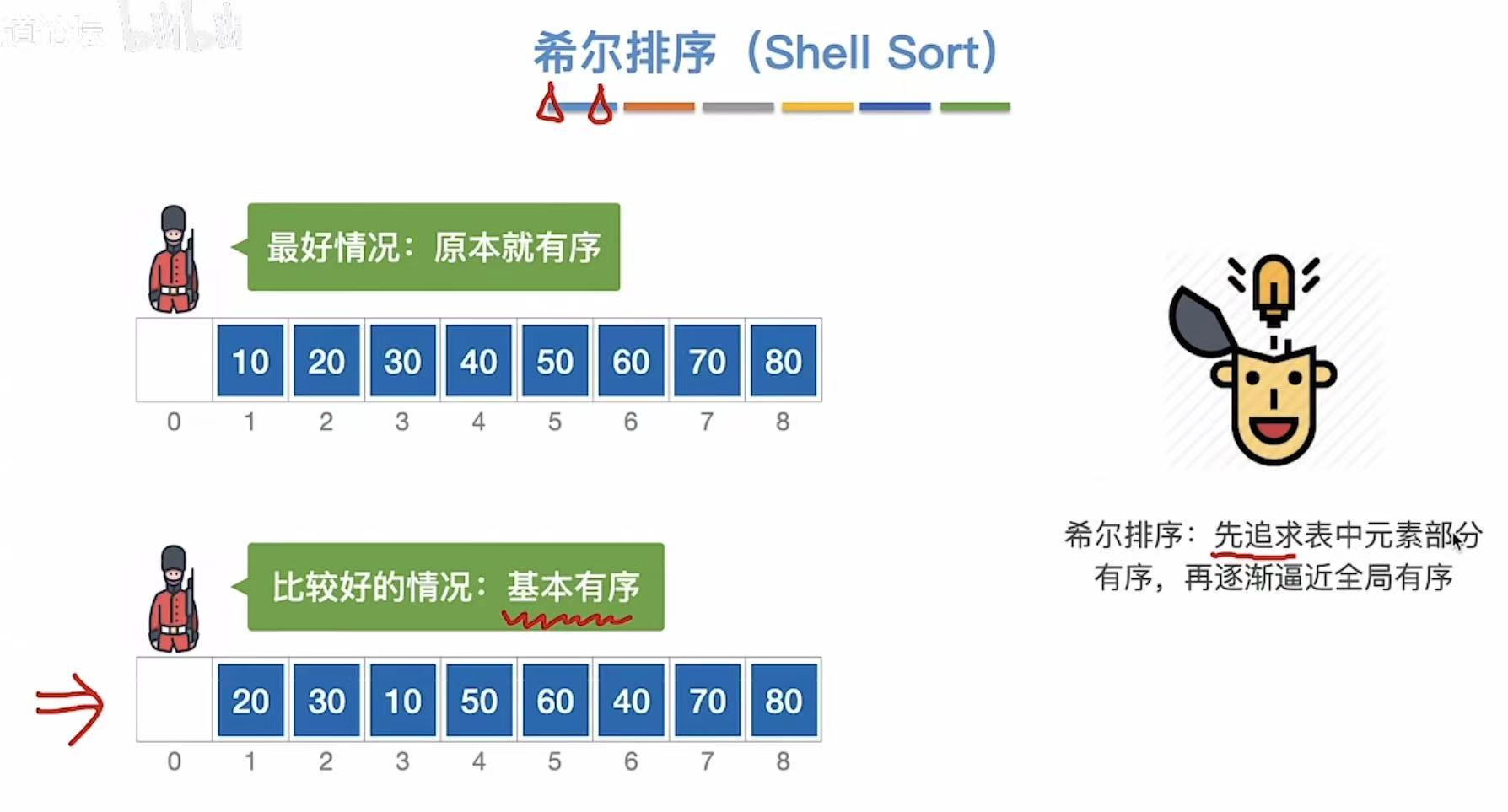
2.1 过程

2.1.1 第一趟

分为四个子表，要求这四个字表中的数字有序：

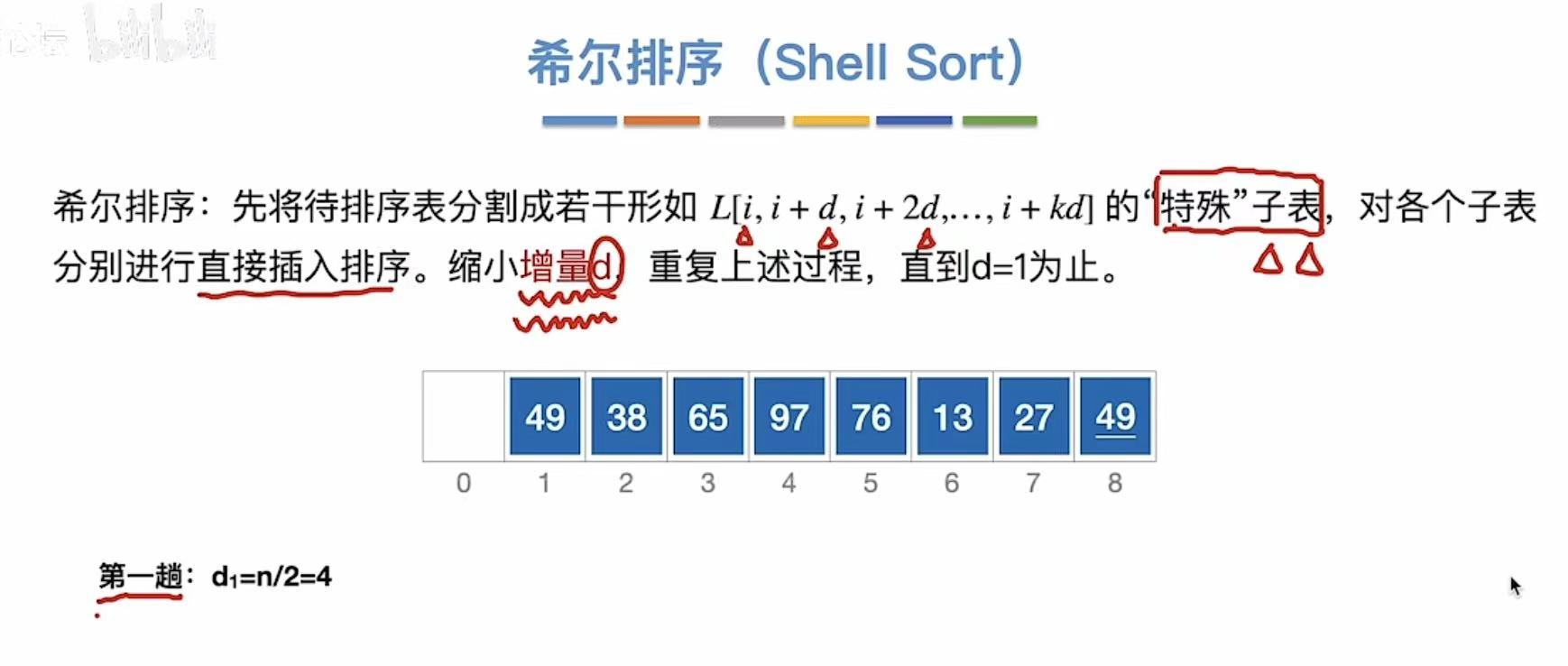
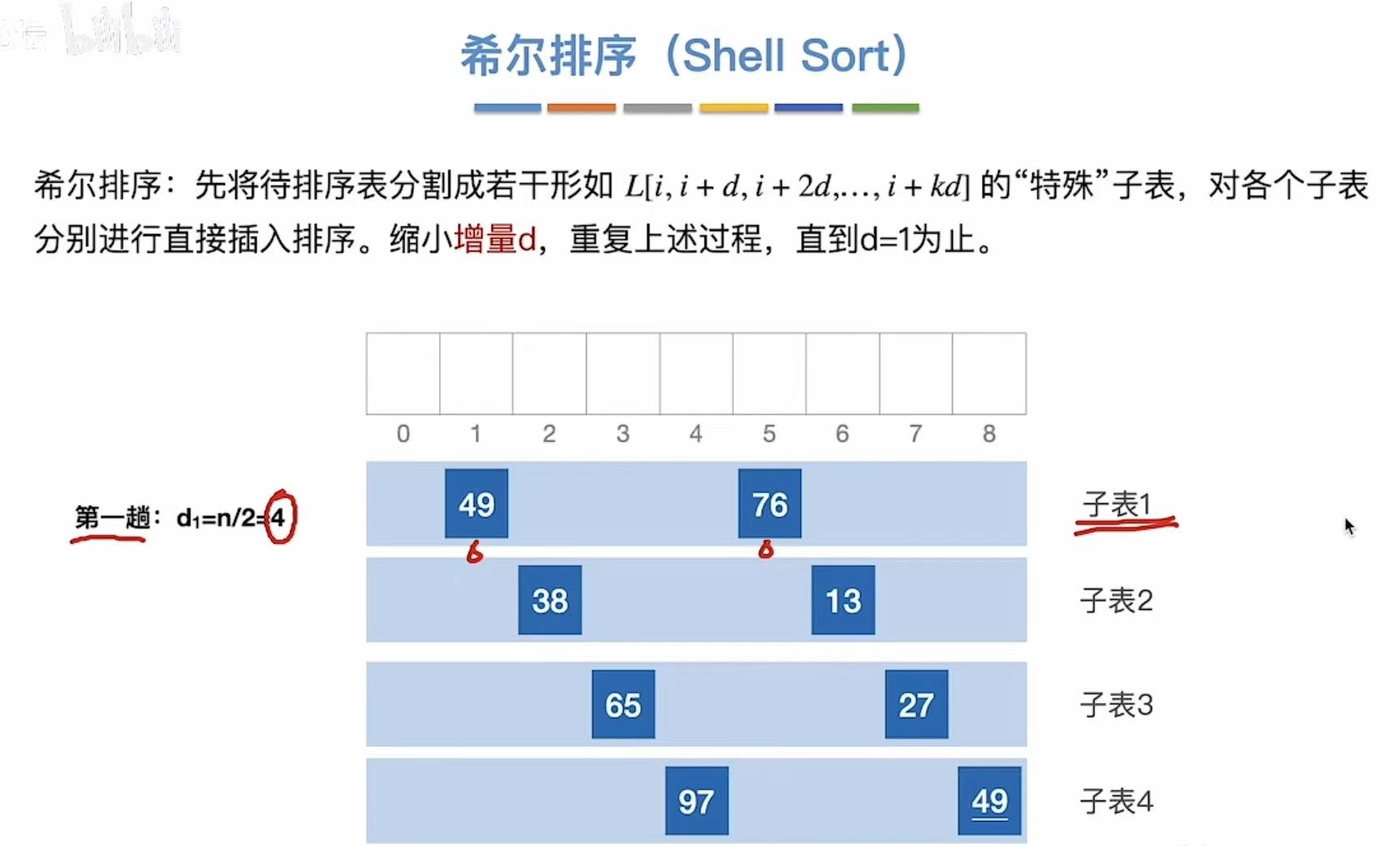
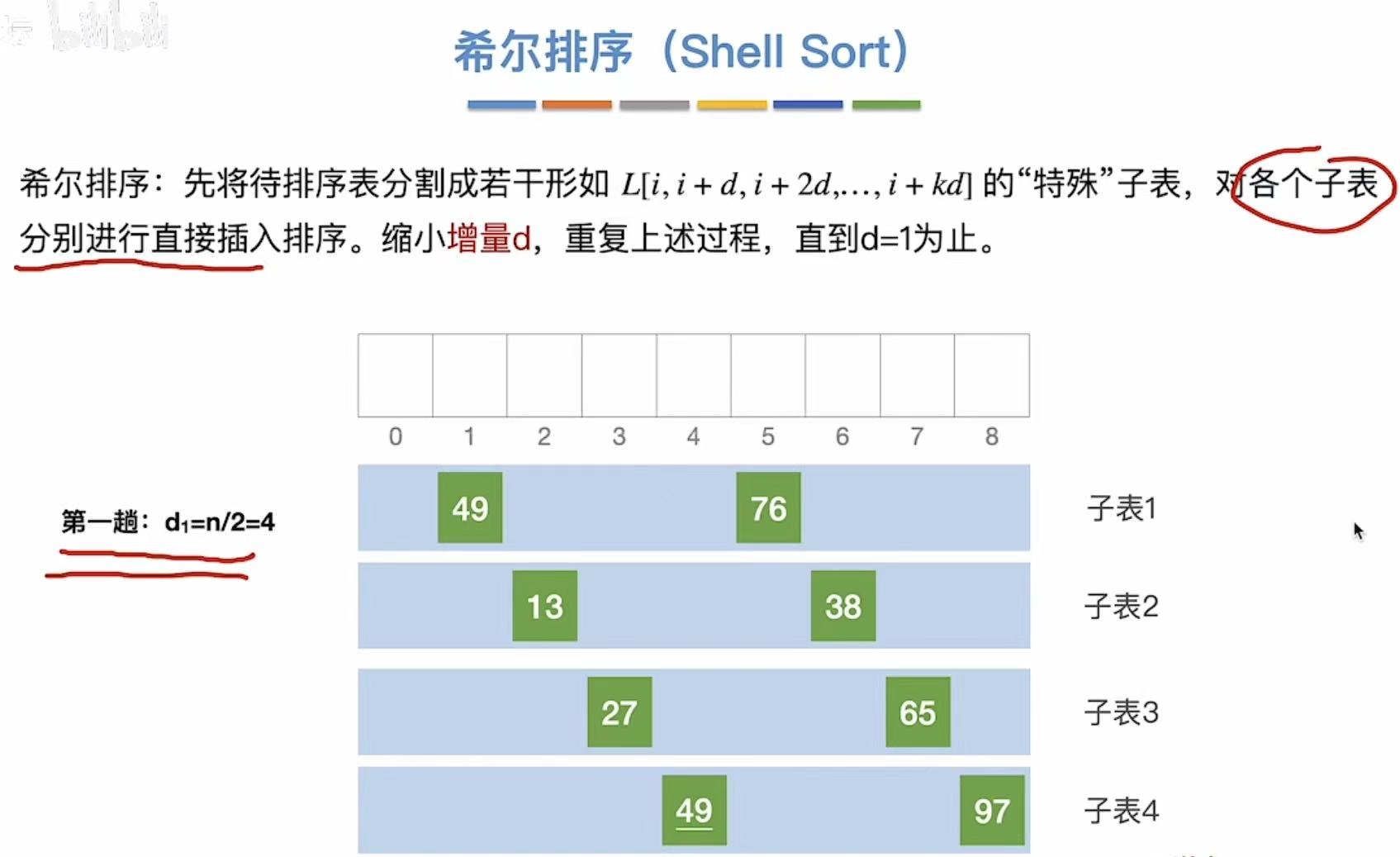
2.1.2 第二趟

分为两个子表，要求这两个字表中的数字有序：

2.1.3 第三趟

分为一个子表，要求这一个字表中的数字有序（其实就是插入排序）：

2.1.4 小结

希尔排序的文字表述：

建议每次的子表都是1/2的关系（增量就是子表的个数）

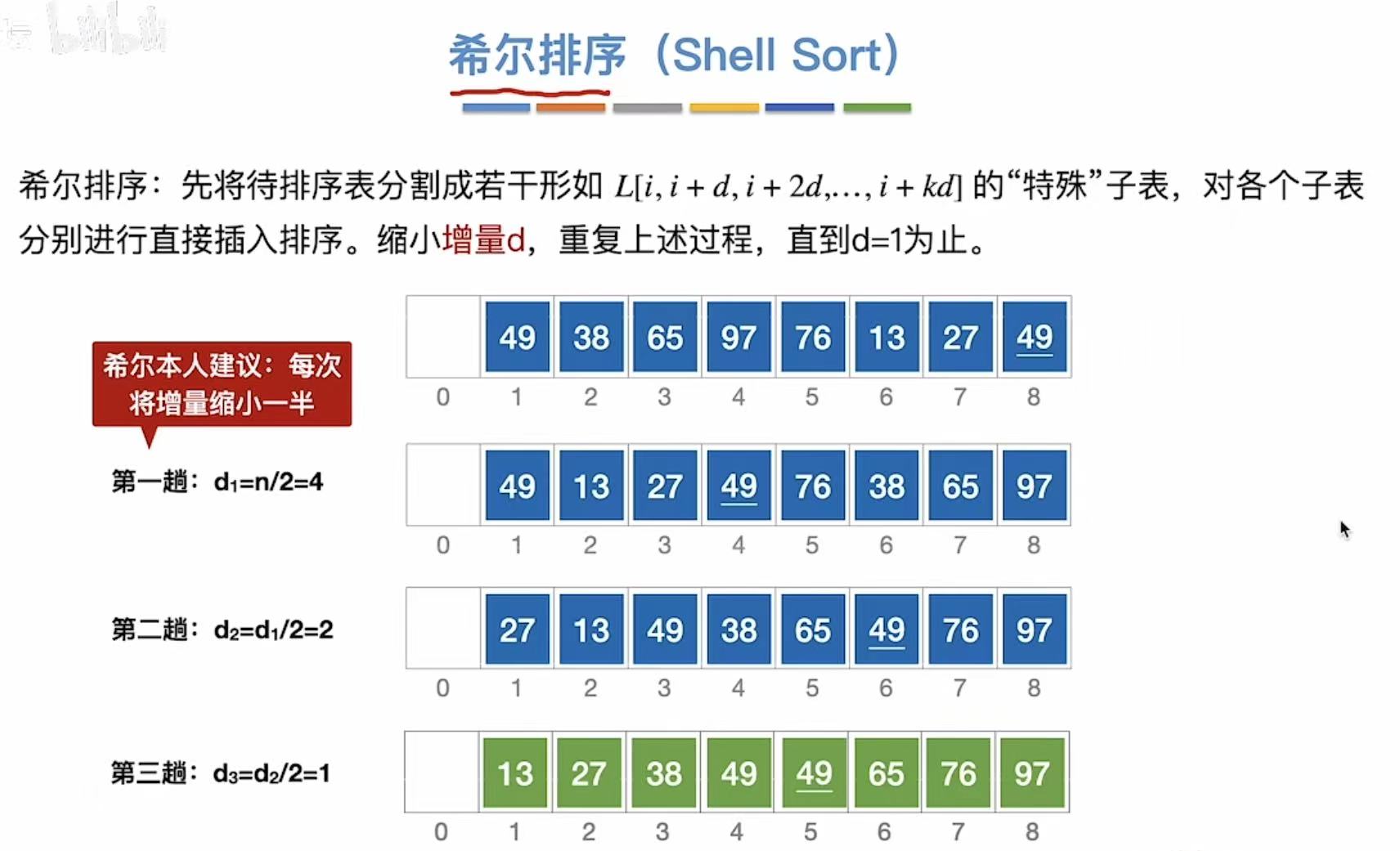
考试的时候可能会遇到不同的增量（就是分成增量个子表）

2.2 算法实现

java 复制代码

// 希尔排序：一种改进的插入排序，通过分组逐步缩小步长进行排序
void ShellSort(int A[], int n) {
    int d, i, j;  // d: 步长（增量）；i: 当前处理元素下标；j: 比较指针

    // 外层循环：步长 d 从 n/2 开始，每次减半，直到 d=1
    // 这是经典的"Hibbard 序列"或"Knuth 序列"的简化版本
    for (d = n / 2; d >= 1; d = d / 2) {  // 步长变化
        // 内层循环：对每个起始位置为 d 的子序列进行直接插入排序
        // 即：将数组分为 d 个子序列，每个子序列中元素相隔 d 个位置
        for (i = d + 1; i <= n; i++) {   // 从第 d+1 个元素开始处理
            // 如果当前元素 A[i] 小于前一个同组元素 A[i-d]，需要插入调整
            if (A[i] < A[i - d]) {
                // 将当前要插入的元素 A[i] 暂存到 A[0]（作为哨兵）
                // 注意：这里 A[0] 不存放实际数据，仅用于简化比较
                A[0] = A[i];

                // 向后移动所有比 A[0] 大的元素，空出插入位置
                // j 从 i-d 开始，每次减 d，即在同一个子序列中向前比较
                for (j = i - d; j > 0 && A[0] < A[j]; j -= d) {
                    A[j + d] = A[j];  // 将较大的元素向后挪 d 个位置
                }

                // 将 A[0]（即原 A[i]）插入到正确位置
                A[j + d] = A[0];
            }
        }
    }
}

2.3 算法性能分析

因为增量是个不确定的因素，而时间复杂度和增量有关，所以也没有确切的时间复杂度。

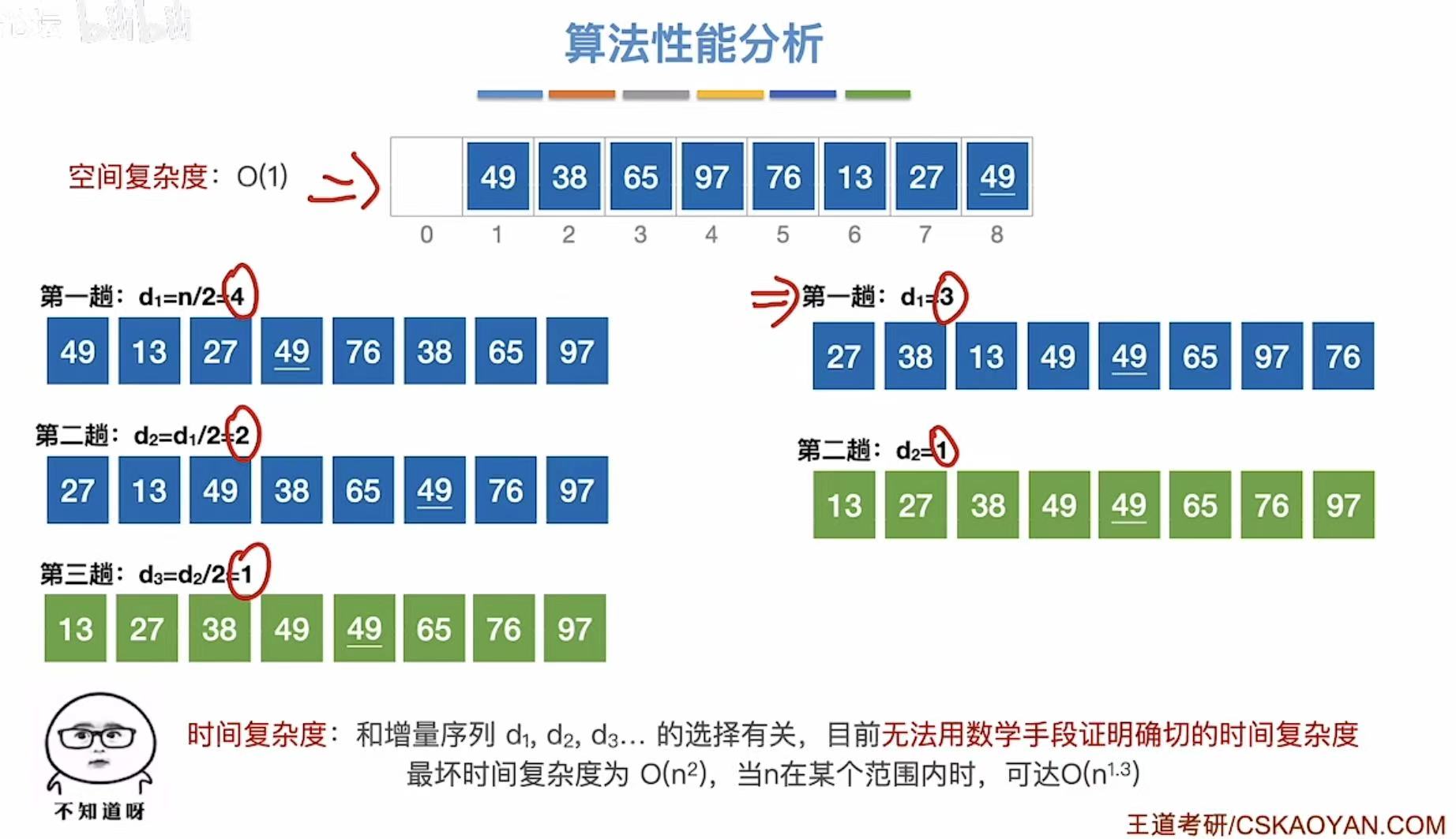
经过排序，相同的两个数字先后顺序发生变化，所以不稳定。

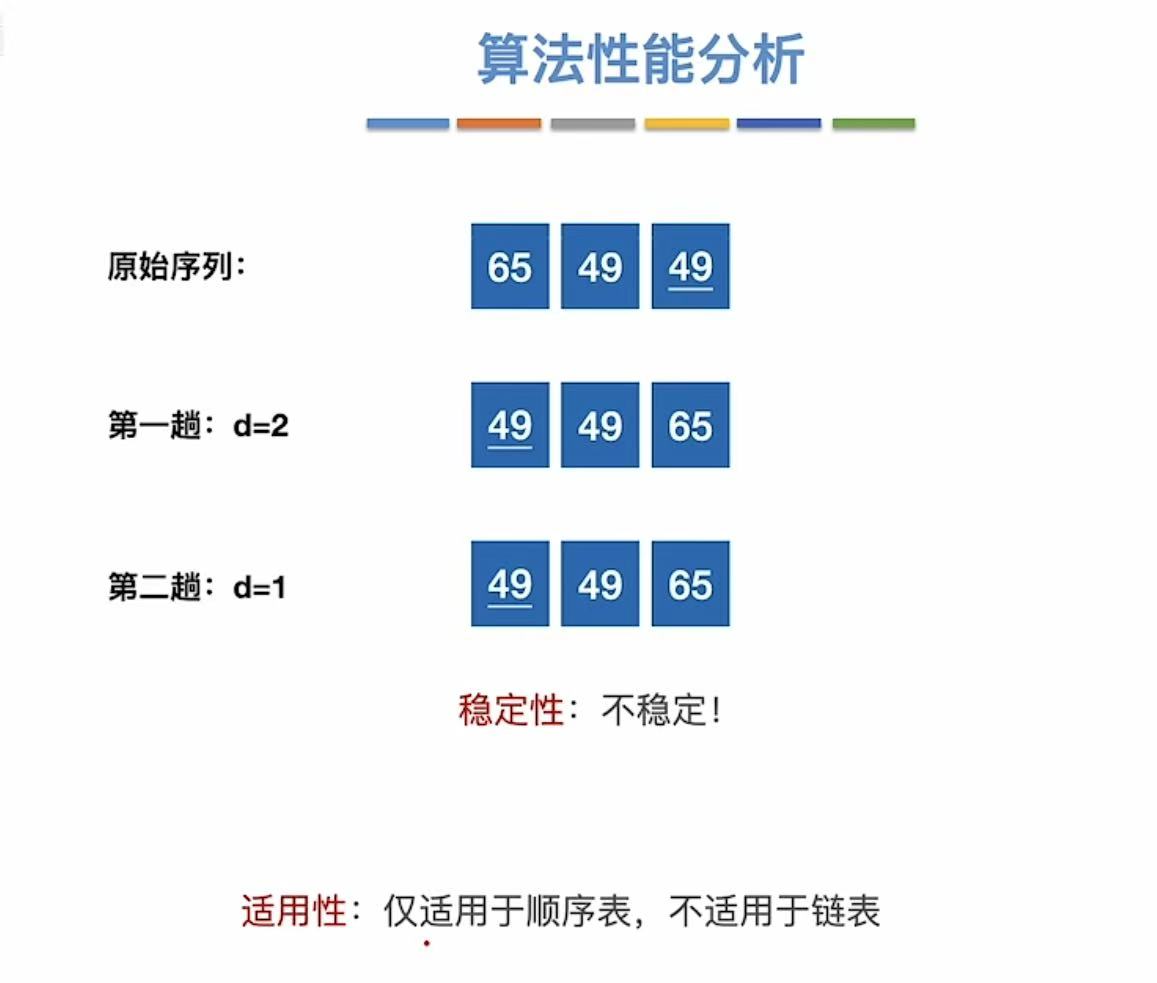
2.4 小结

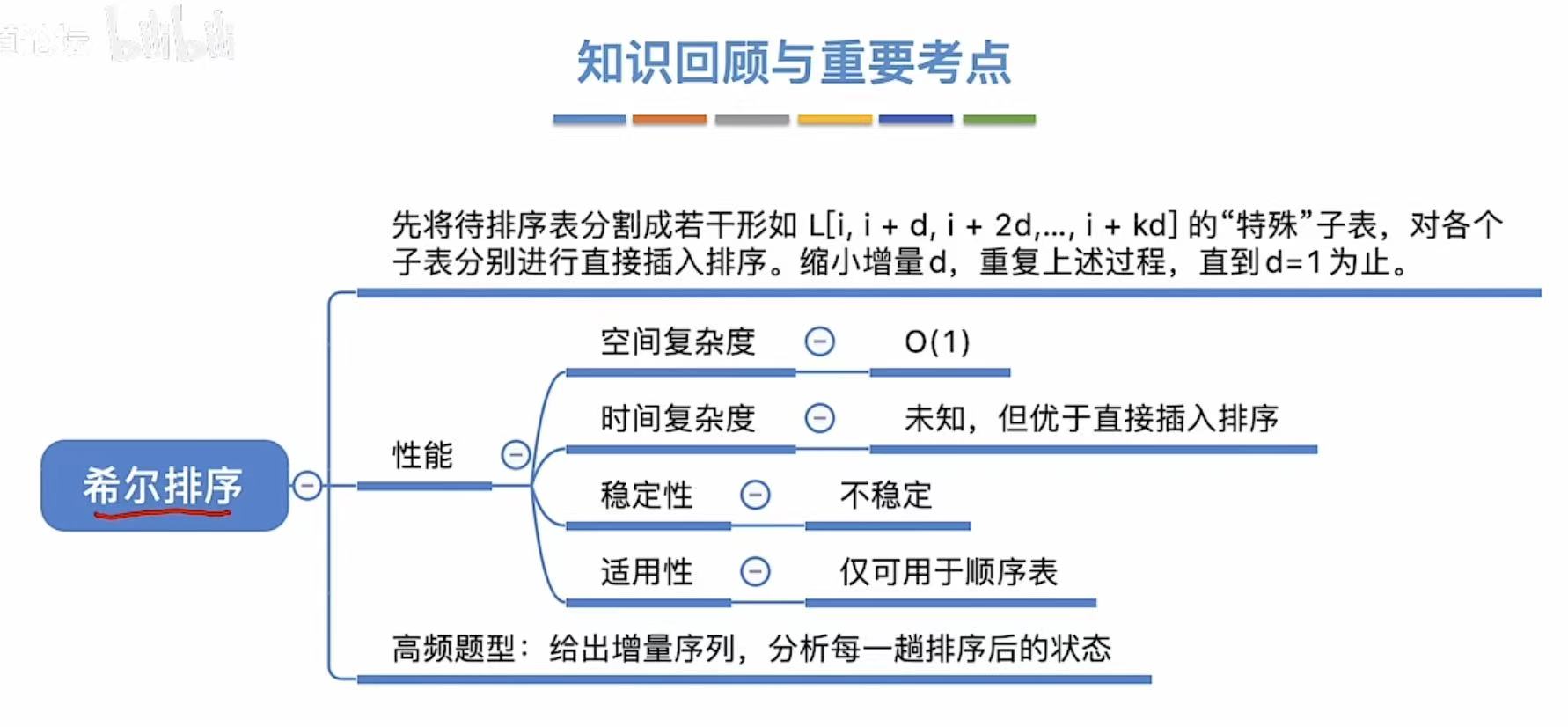
3. 交换排序

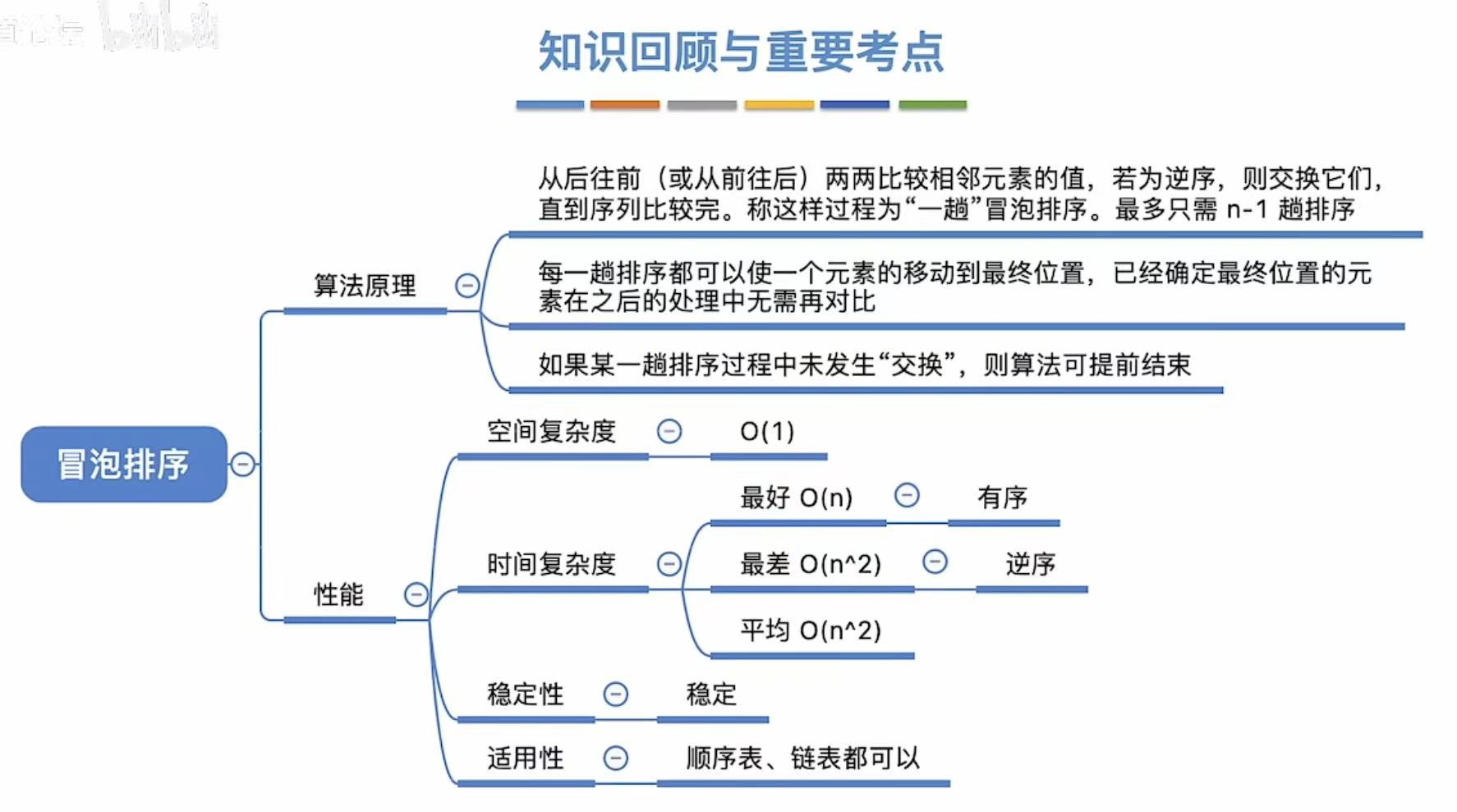
3.1 冒泡排序

3.1.1 过程

从后往前，两个两个之间进行交换。（进行n轮）

3.1.1.1 第一趟

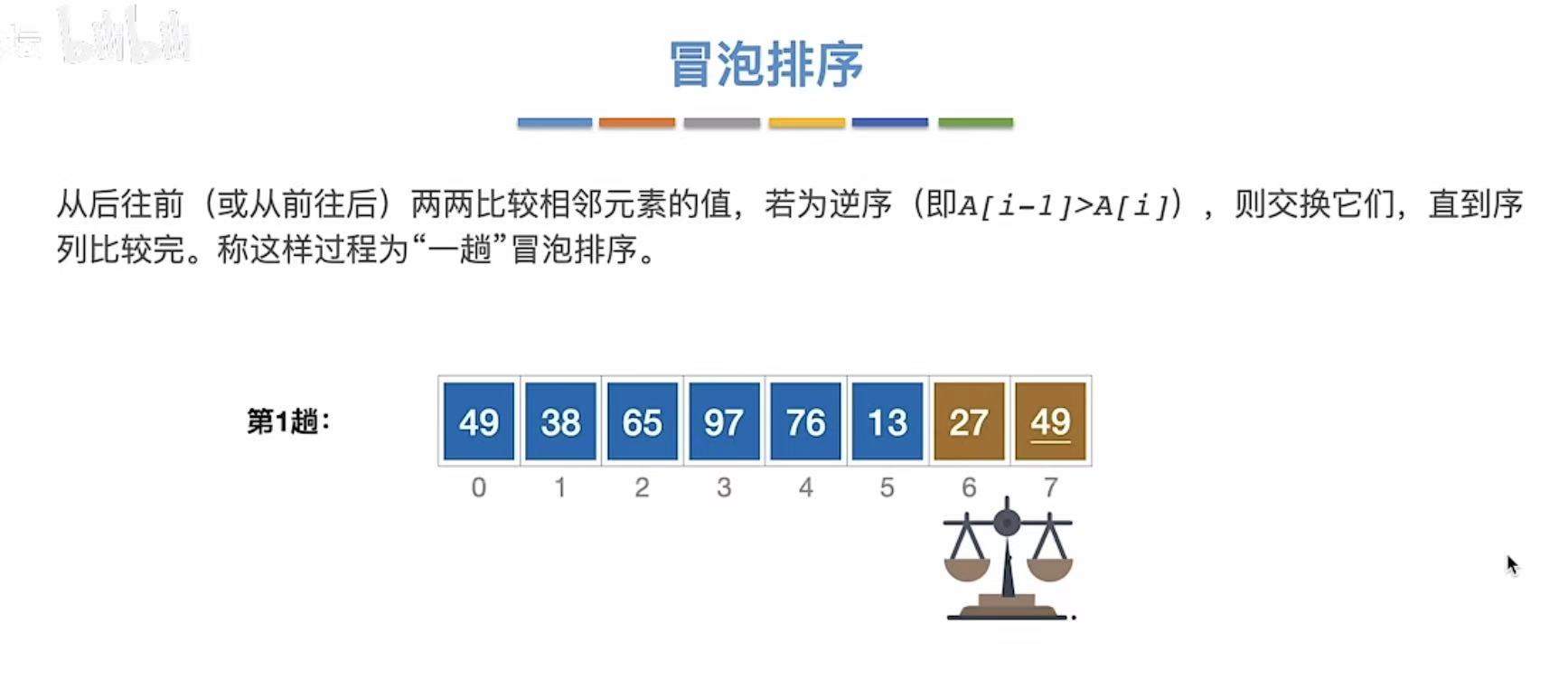
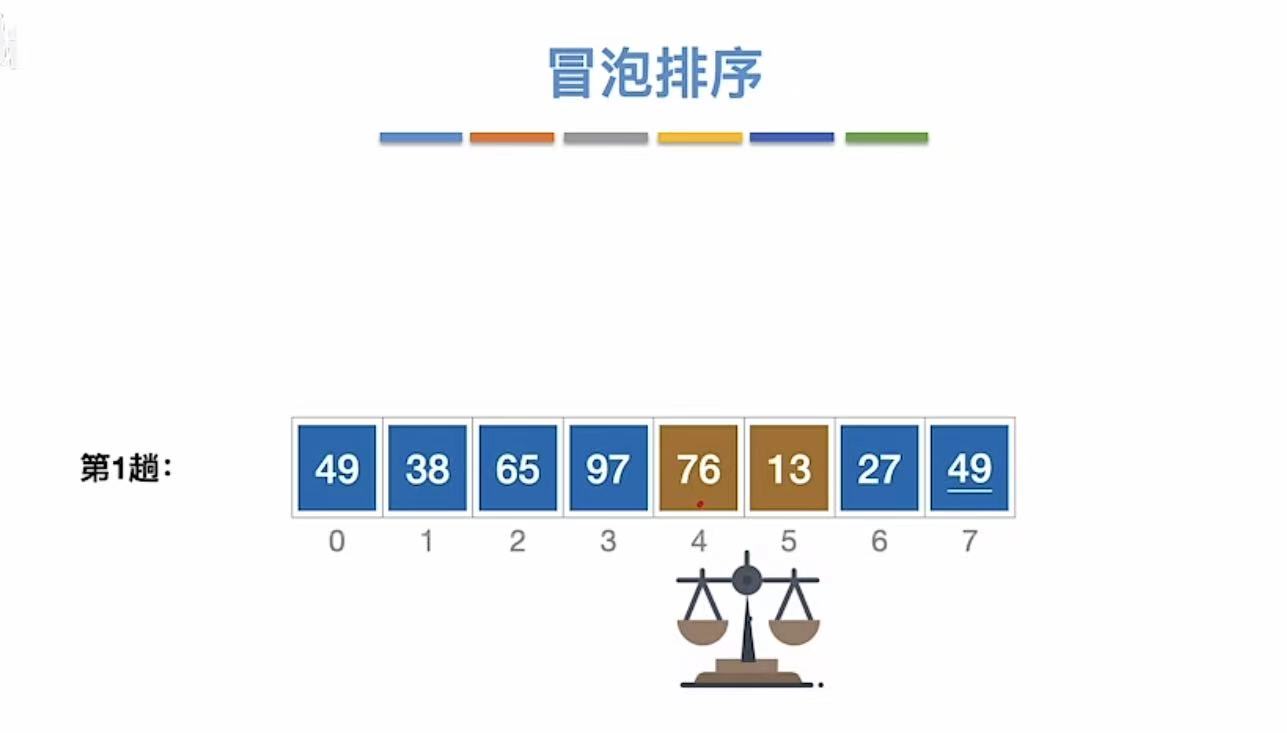
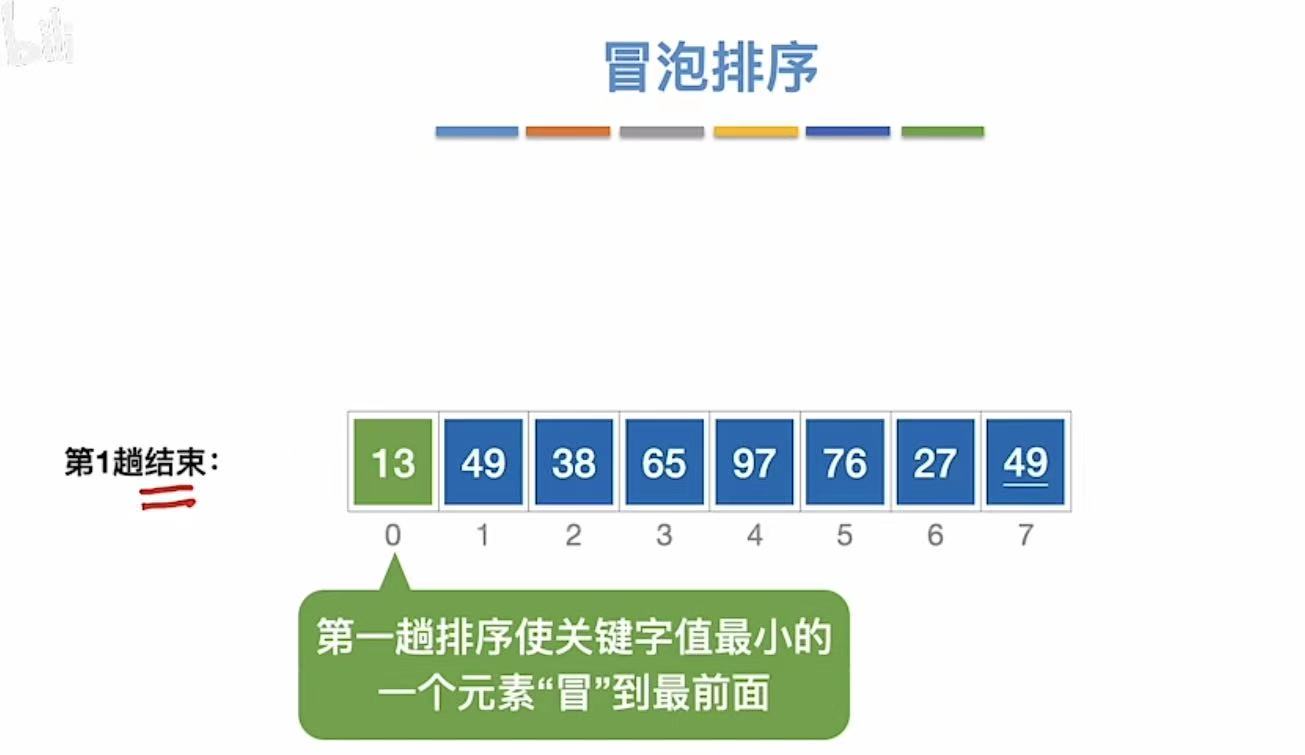
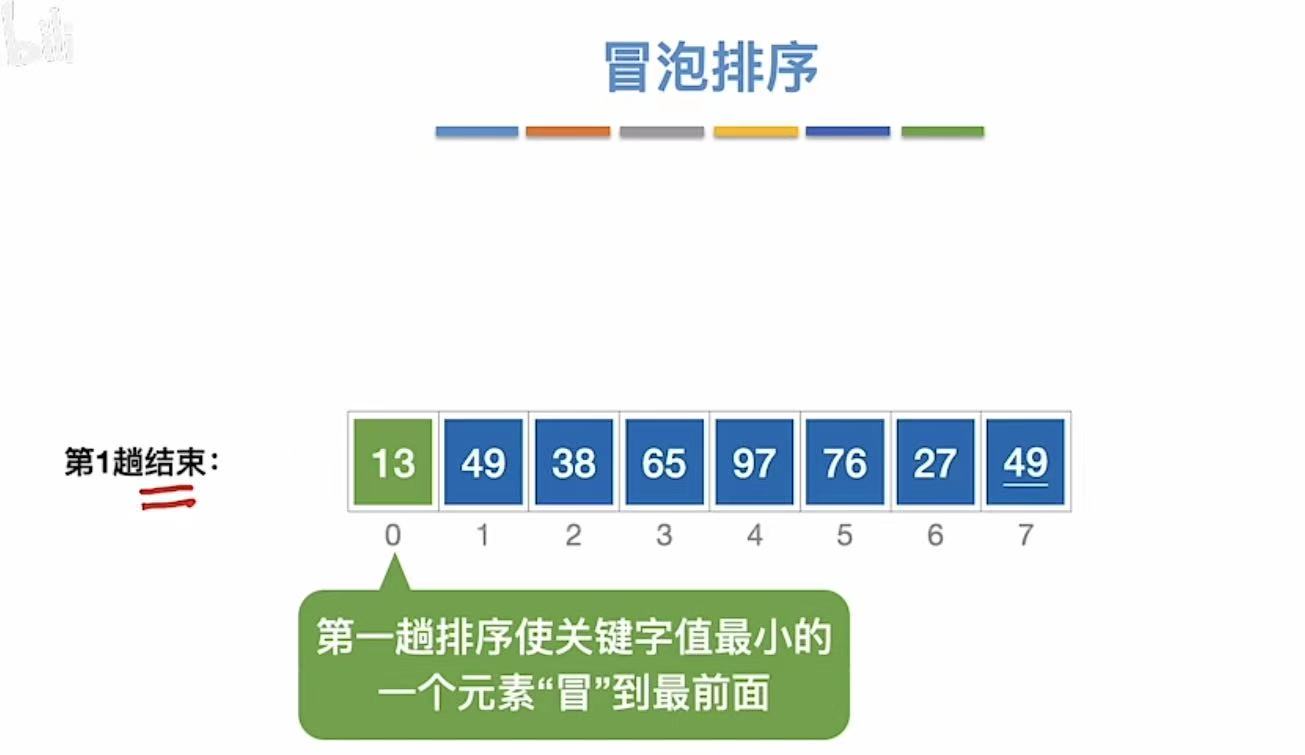
3.1.1.2 第二趟

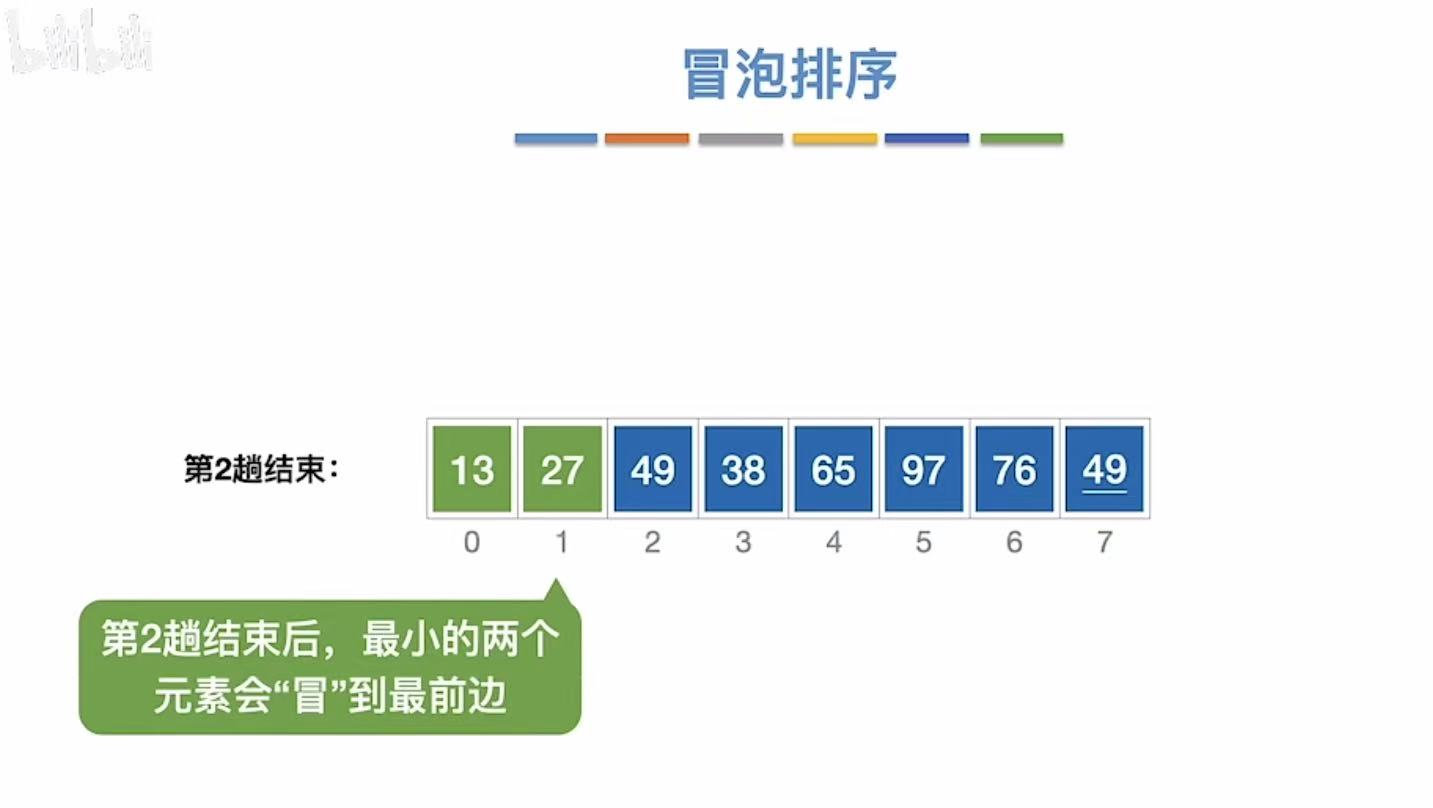
3.1.1.3 第三趟

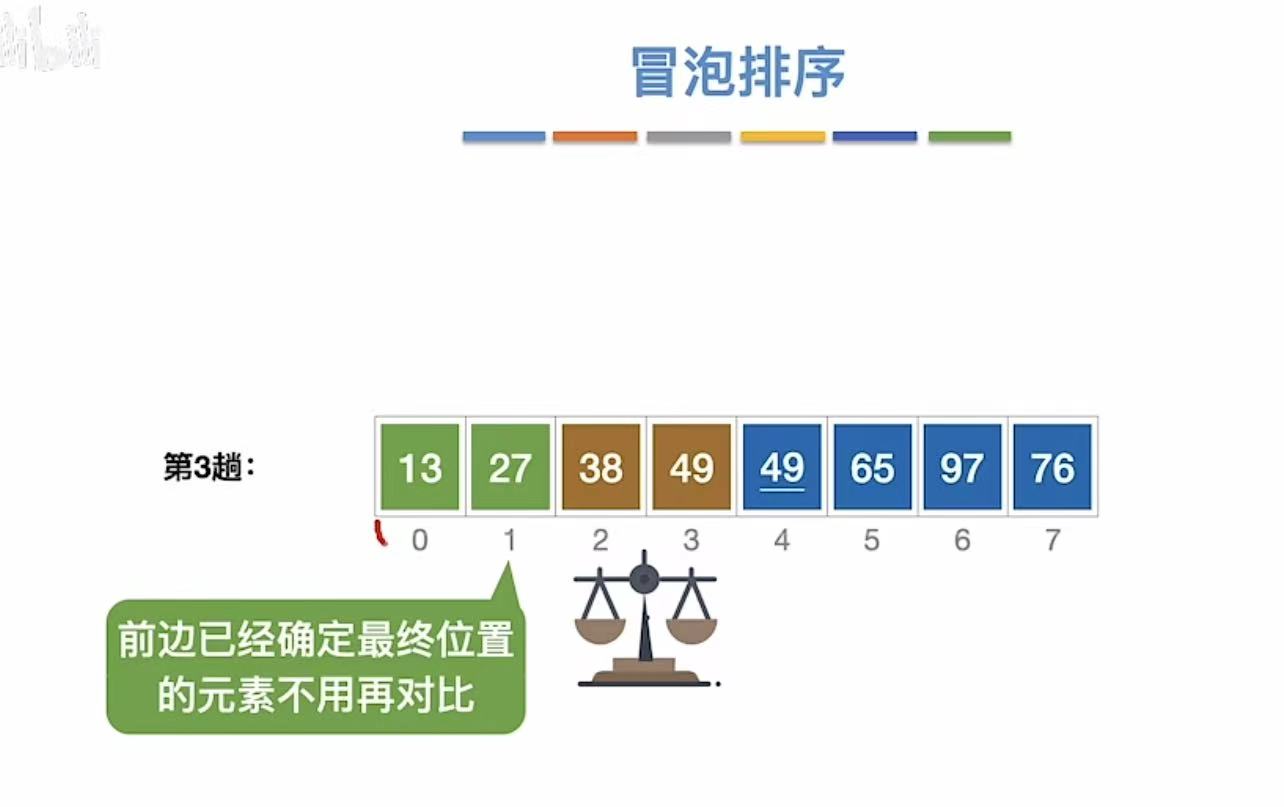
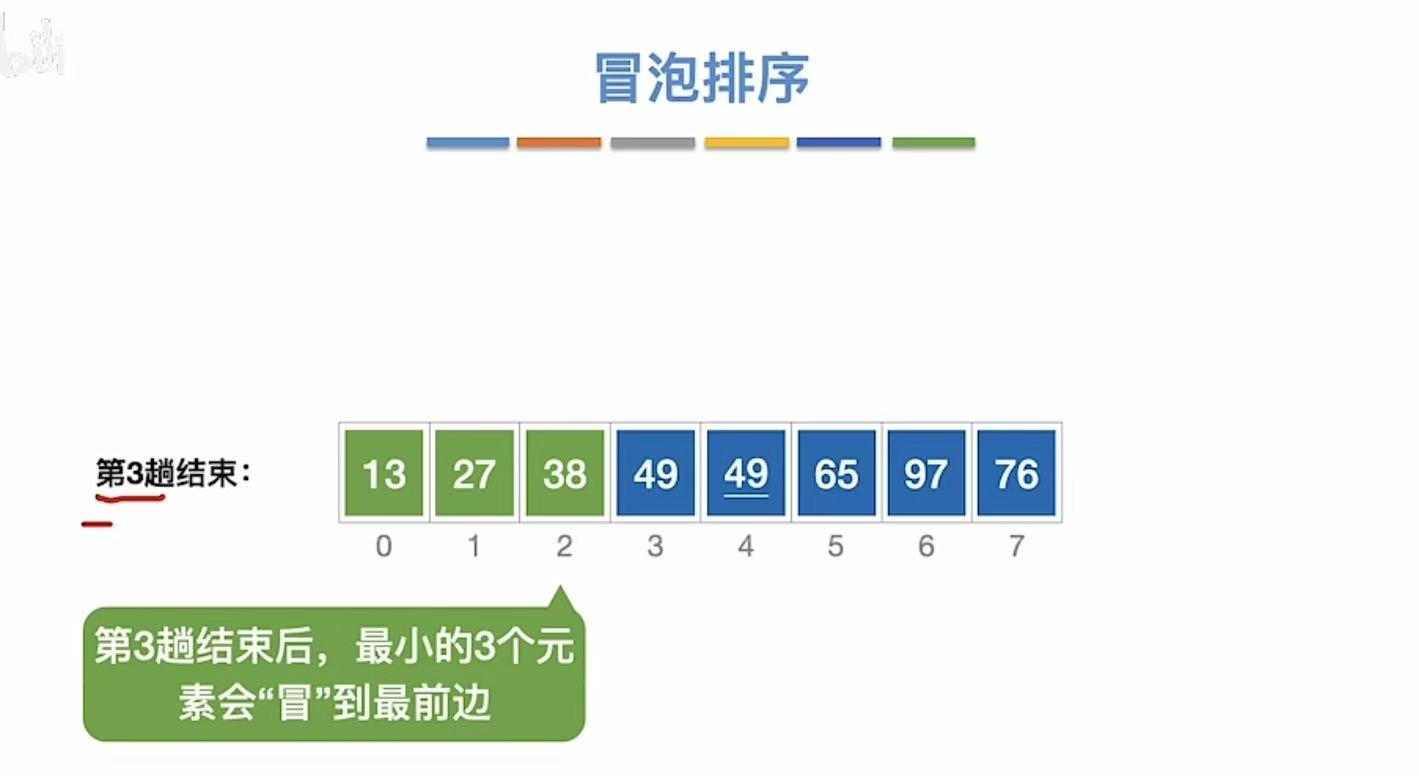
3.1.1.4 第四趟

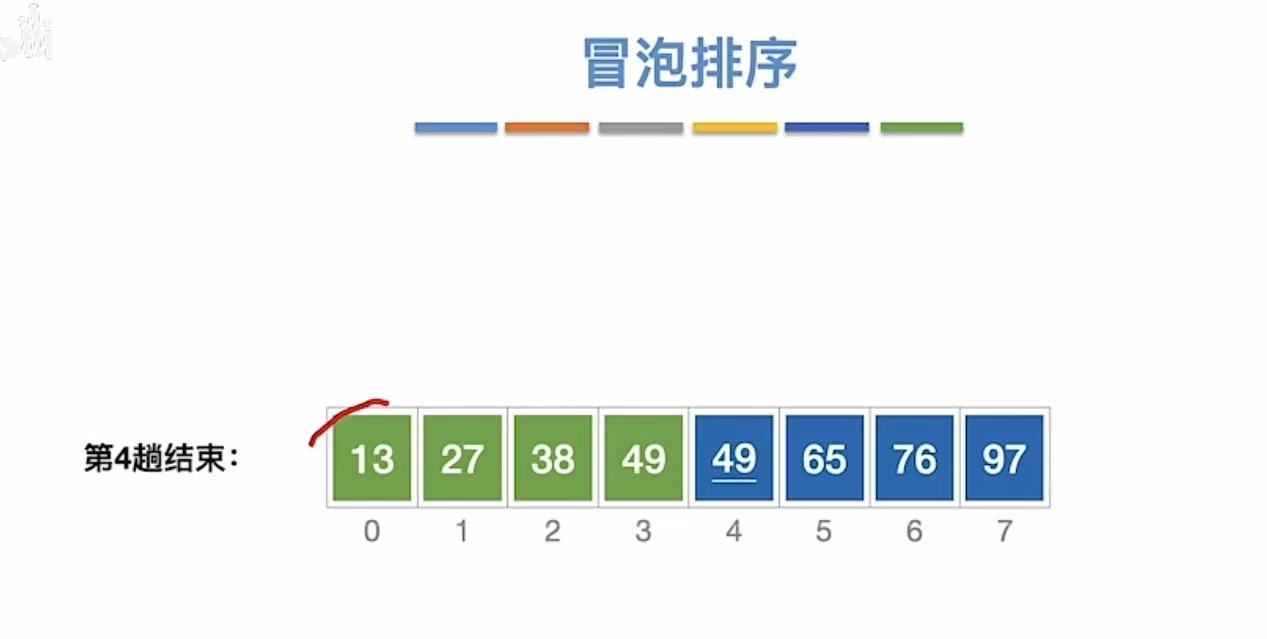
3.1.1.5 第五趟

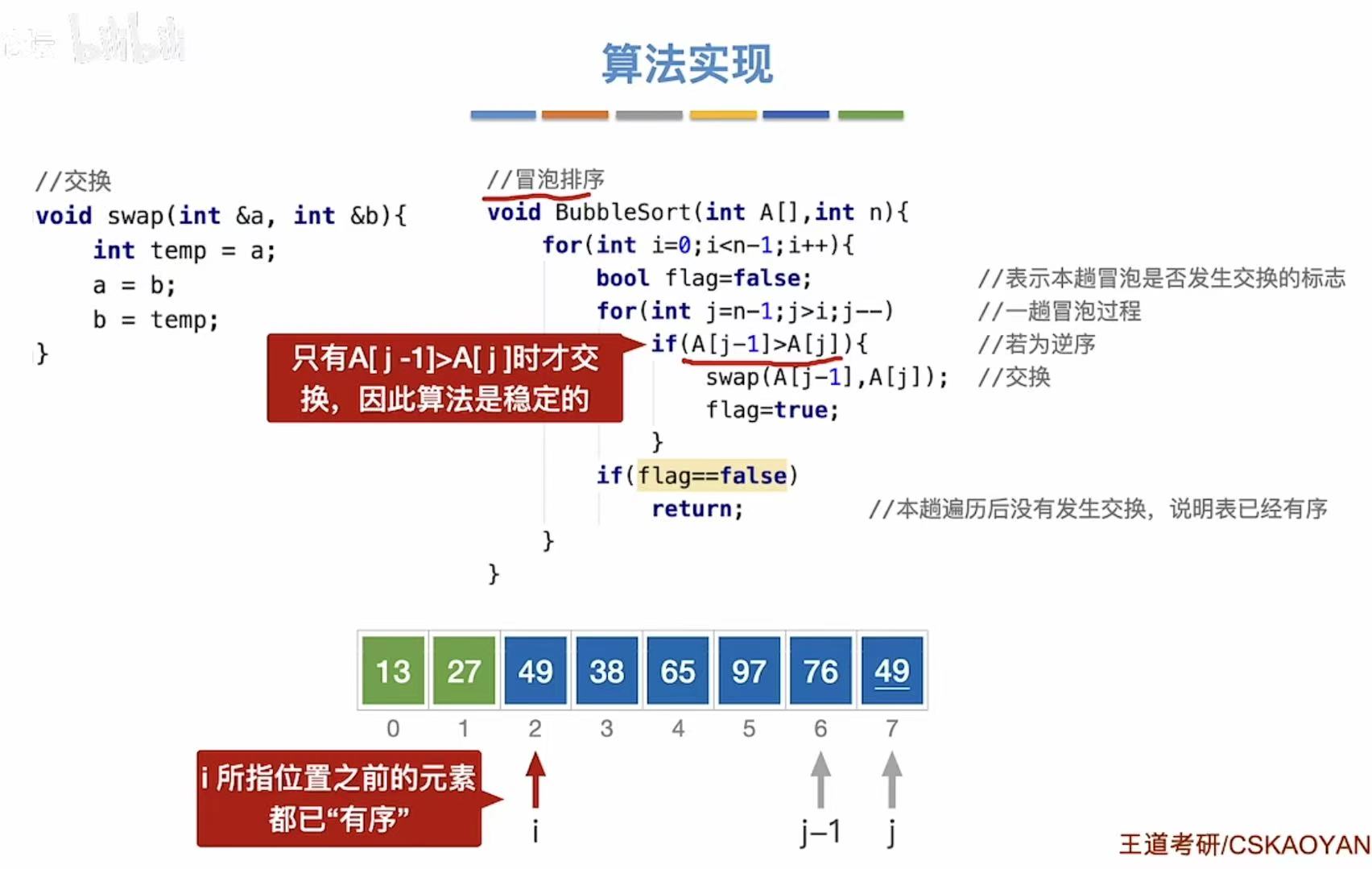
3.1.2 算法实现

java 复制代码

// 交换函数：交换两个整数的值
void swap(int &a, int &b) {  // 使用引用传递，直接修改原变量
    int temp = a;            // 用临时变量保存 a 的值
    a = b;                   // 将 b 的值赋给 a
    b = temp;                // 将 temp（原 a）赋给 b
}

// 冒泡排序：通过相邻元素比较并交换，将最大值"冒泡"到末尾
void BubbleSort(int A[], int n) {
    // 外层循环：控制排序轮数，最多 n-1 轮
    for (int i = 0; i < n - 1; i++) {
        bool flag = false;   // 标志位：记录本轮是否发生交换

        // 内层循环：每轮从后往前比较相邻元素
        // j 从 n-1 开始，每次减 1，直到 i 结束
        for (int j = n - 1; j > i; j--) {
            // 如果前一个元素大于后一个元素（逆序），则交换
            if (A[j - 1] > A[j]) {
                swap(A[j - 1], A[j]);  // 交换相邻元素
                flag = true;           // 标记本轮发生了交换
            }
        }

        // 如果本轮没有发生任何交换，说明数组已经有序
        if (flag == false)
            return;  // 提前结束，优化性能
    }
}

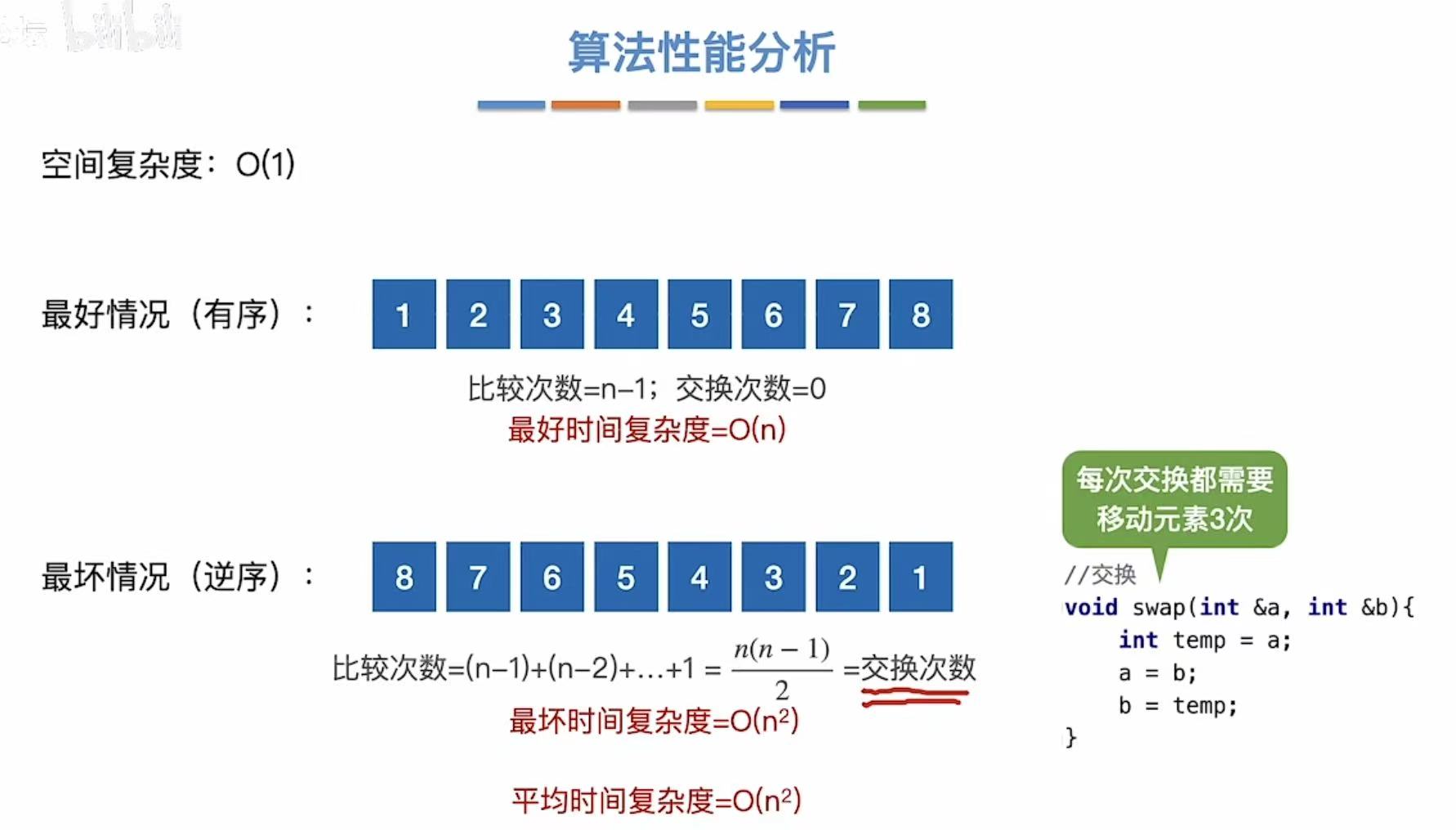
3.1.3 算法性能分析

3.1.4 小结

3.2 快速排序

3.2.1 算法思想

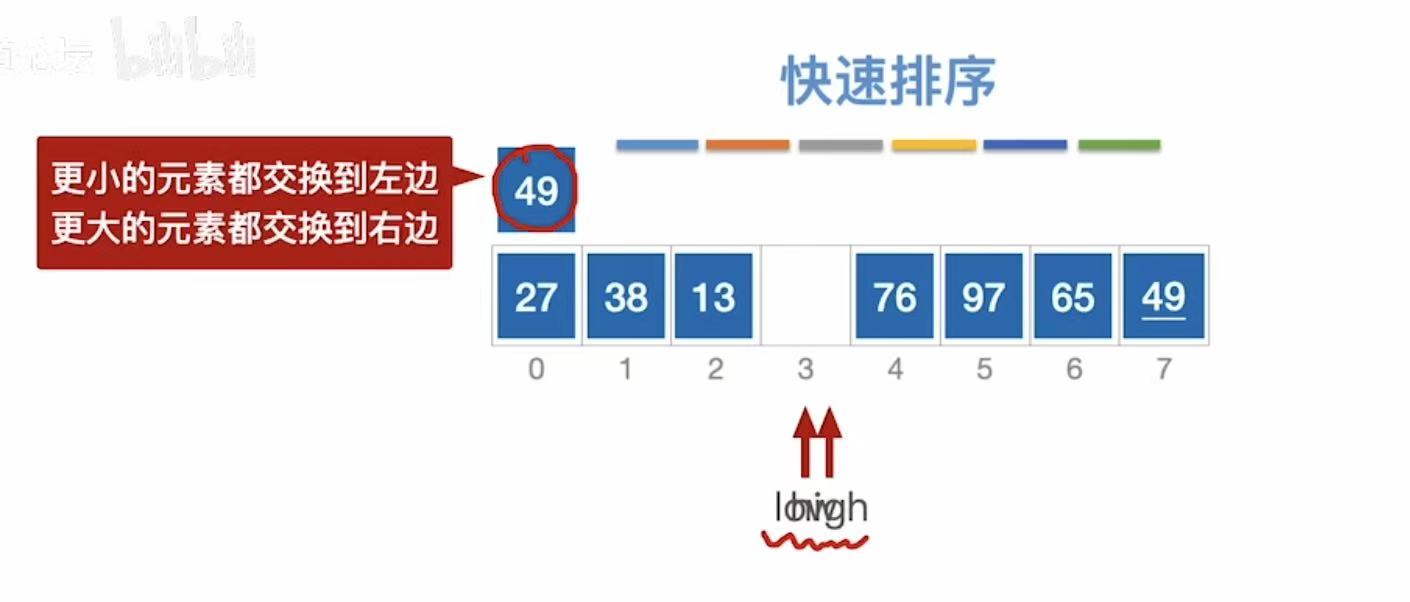
以第一个数字为基准，小于它的就插入到左边，大于它的就插入到右边。（进行n轮）

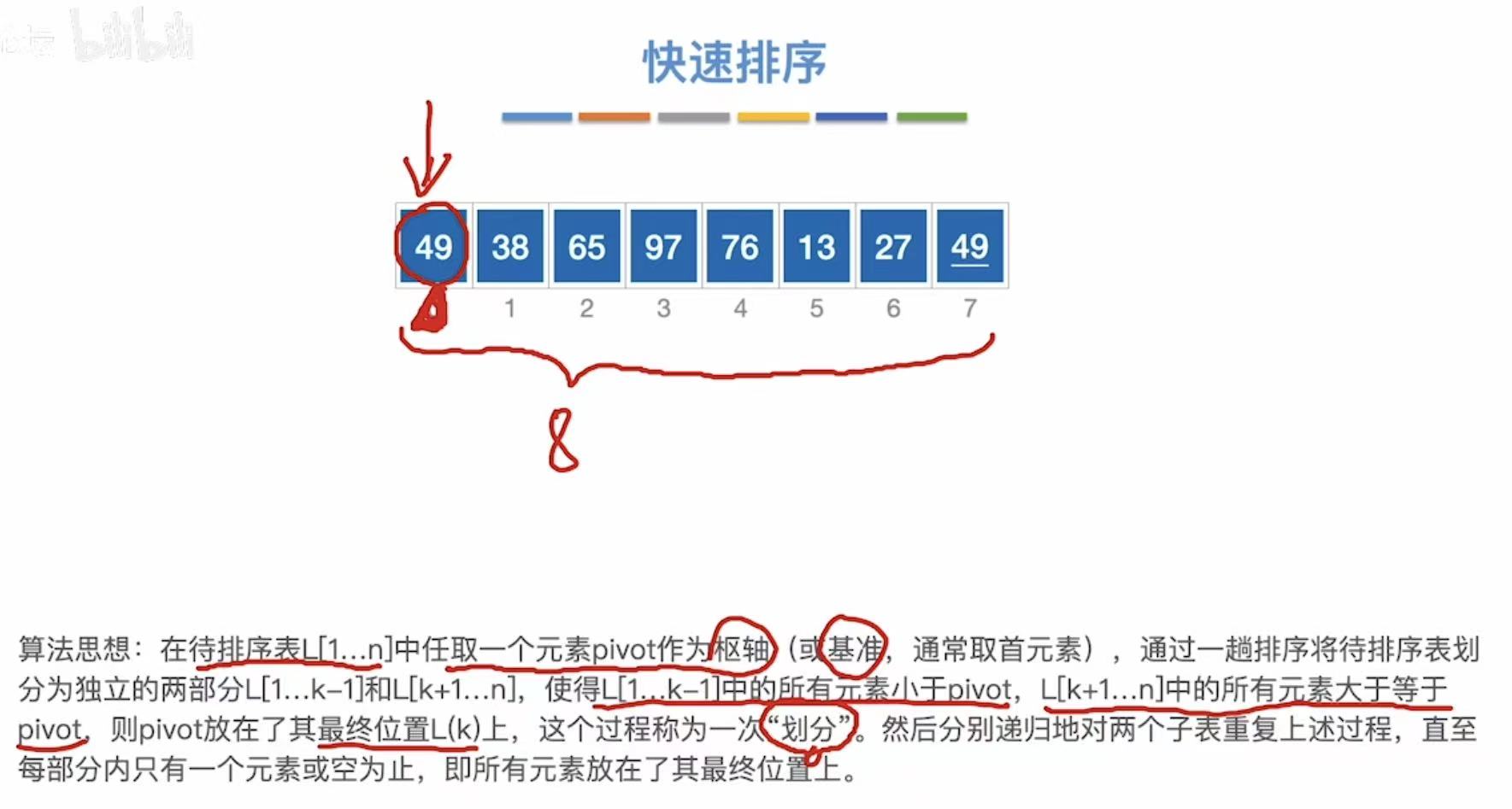
49为基准线：

low指向空，不管；
high指向49，和基准49比，等于49，49不动
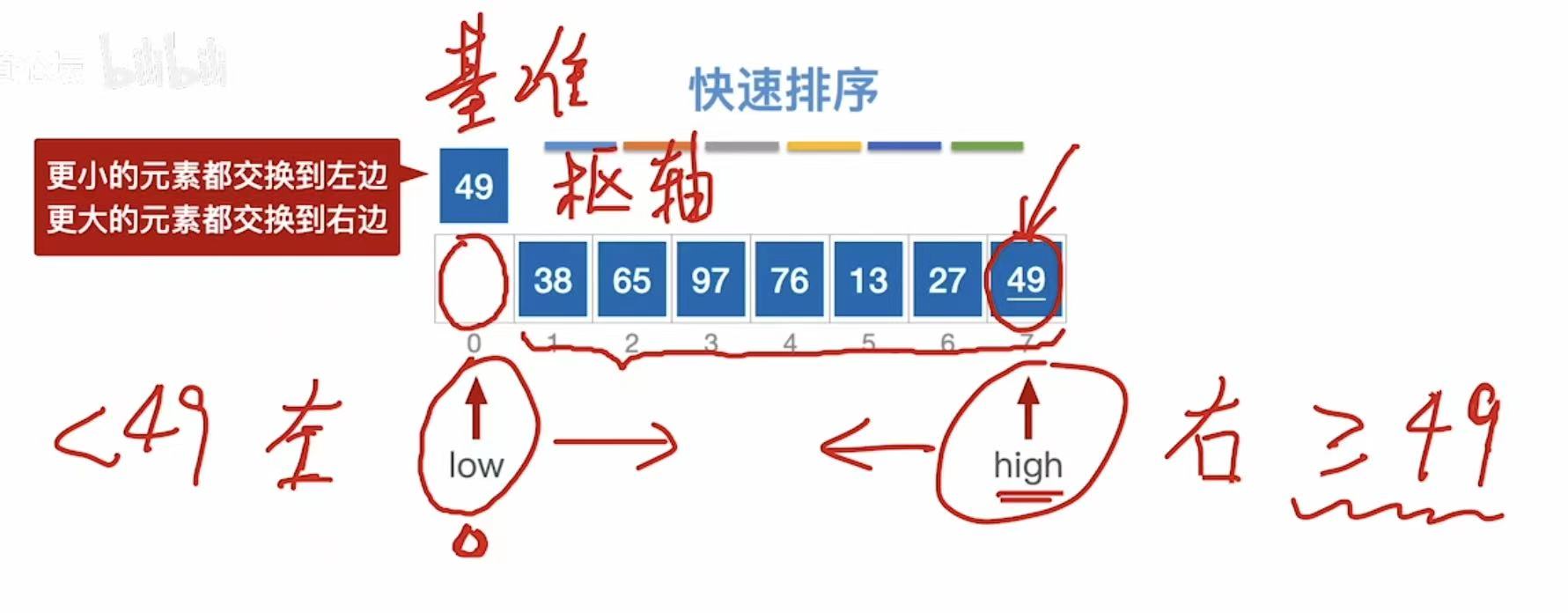
high--，指向27，27<49
27插入到low指向的位置

此时：

low++，指向38
high指向空，不动
low指向38，38<49，38不动
high依旧指向空，不动
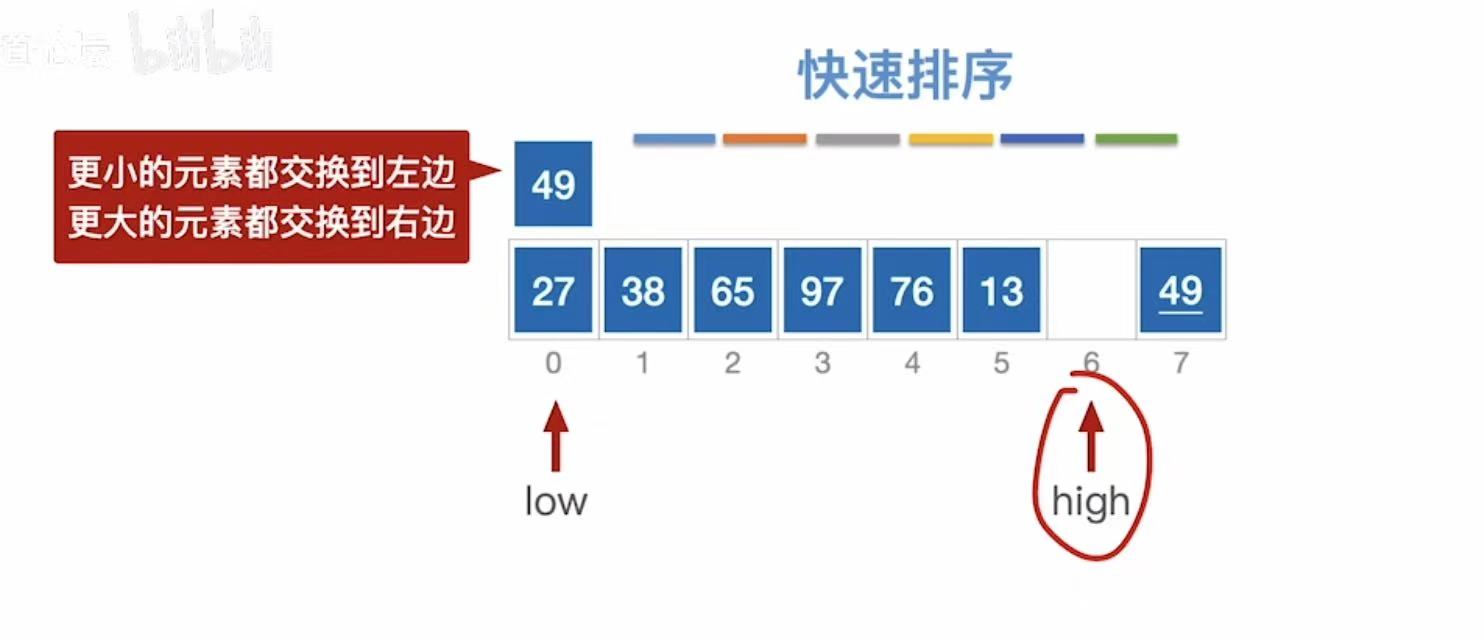
low++，指向65，65>49，65插入到high的位置；

此时：

low指向空，不管；
high指向65，high--；
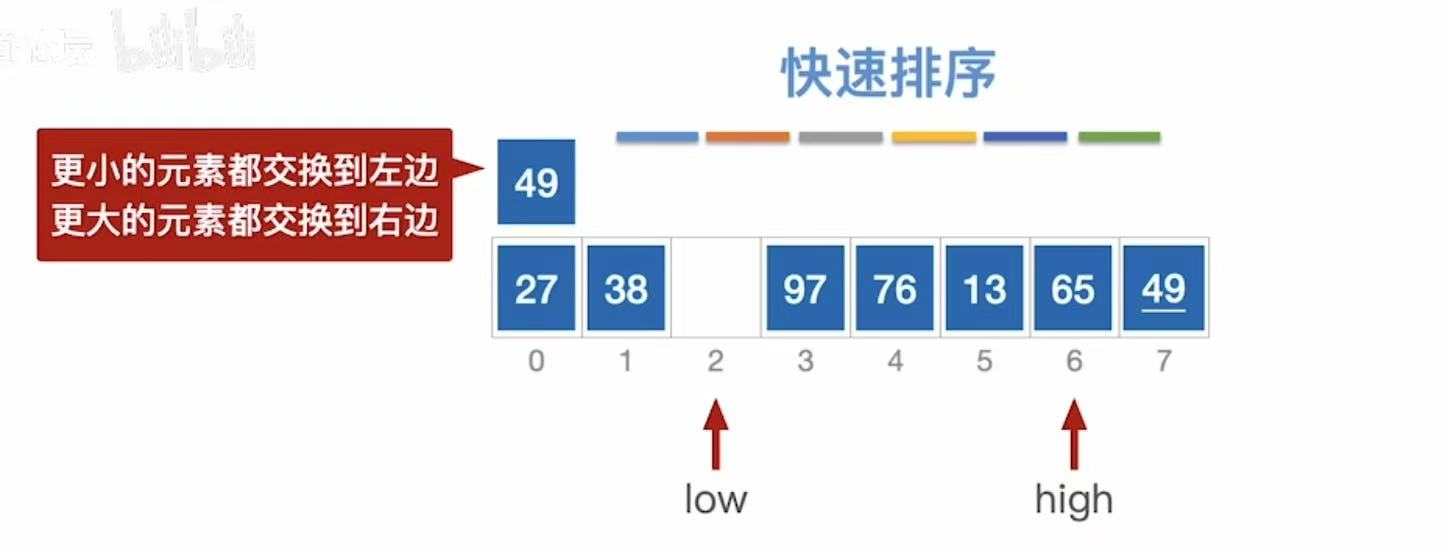
low指向空，不管；
high指向13，13<49，13插入到low的位置

此时：

low指向13，low++；
high指向空，不管
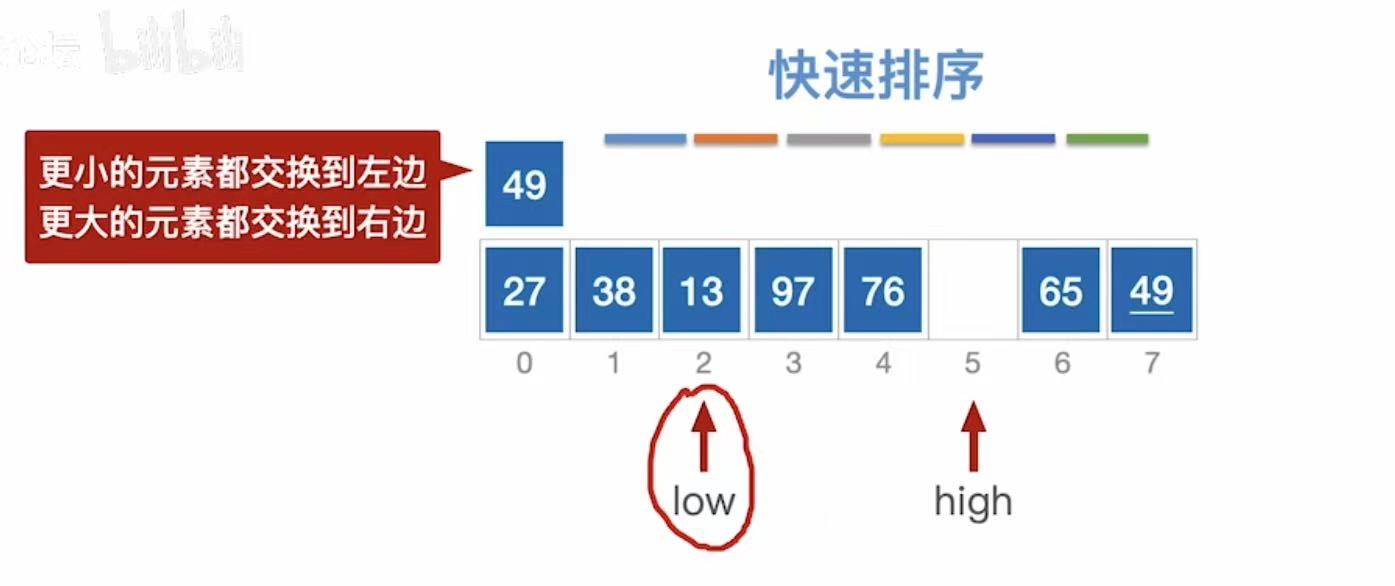
low指向97，97>49，97插入到high的位置，high--；

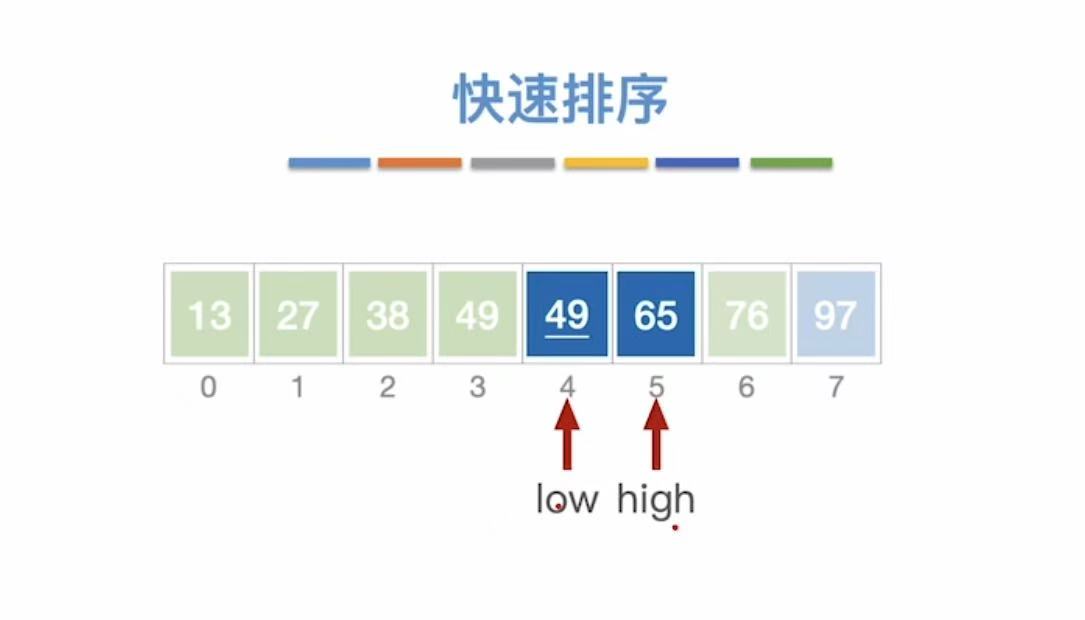
此时：

low指向空，不动
high--指向76，76>49，不动，high--；
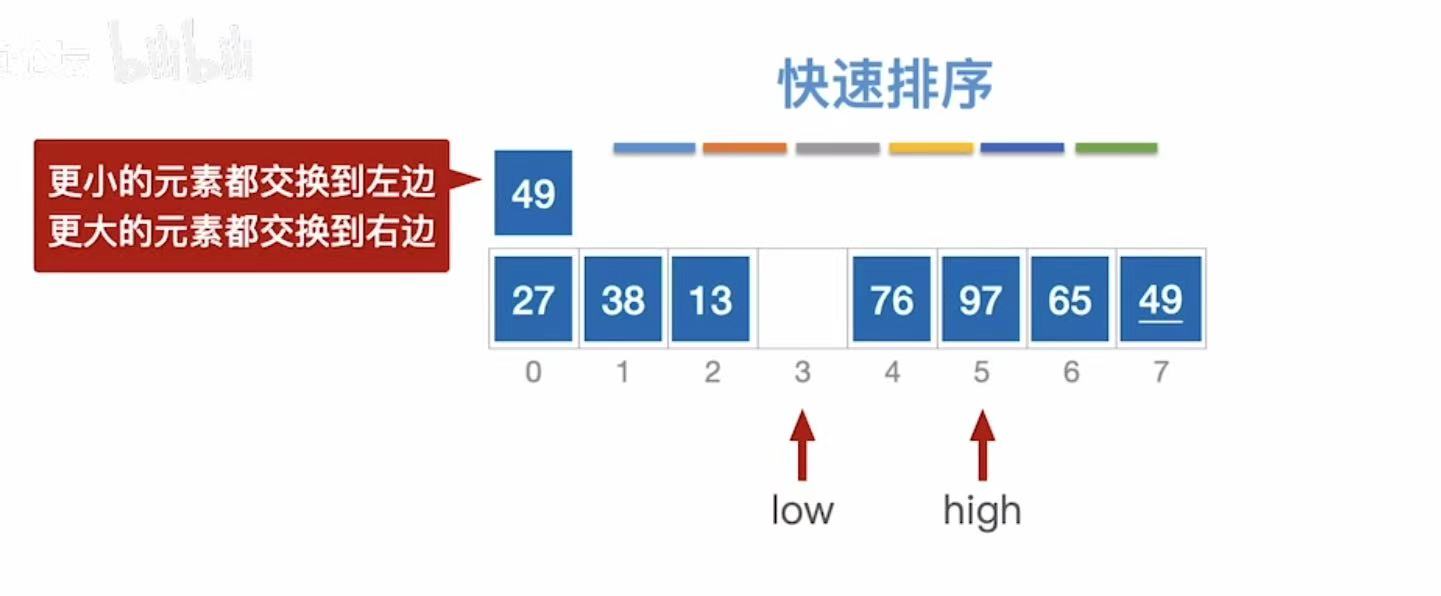
low指向空，low不动
high--指向空；
此时被指的空间就是基准值49该插入的位置

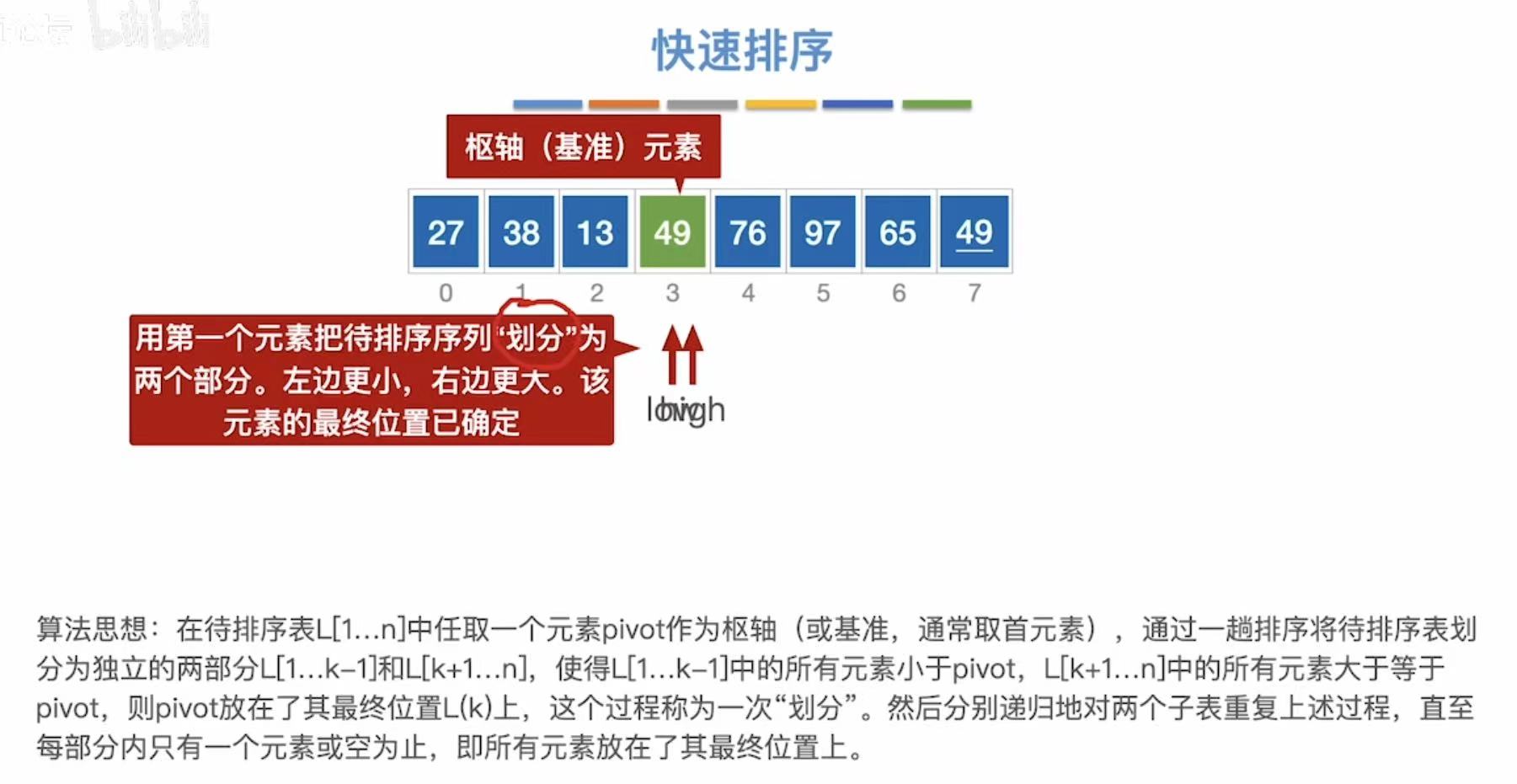
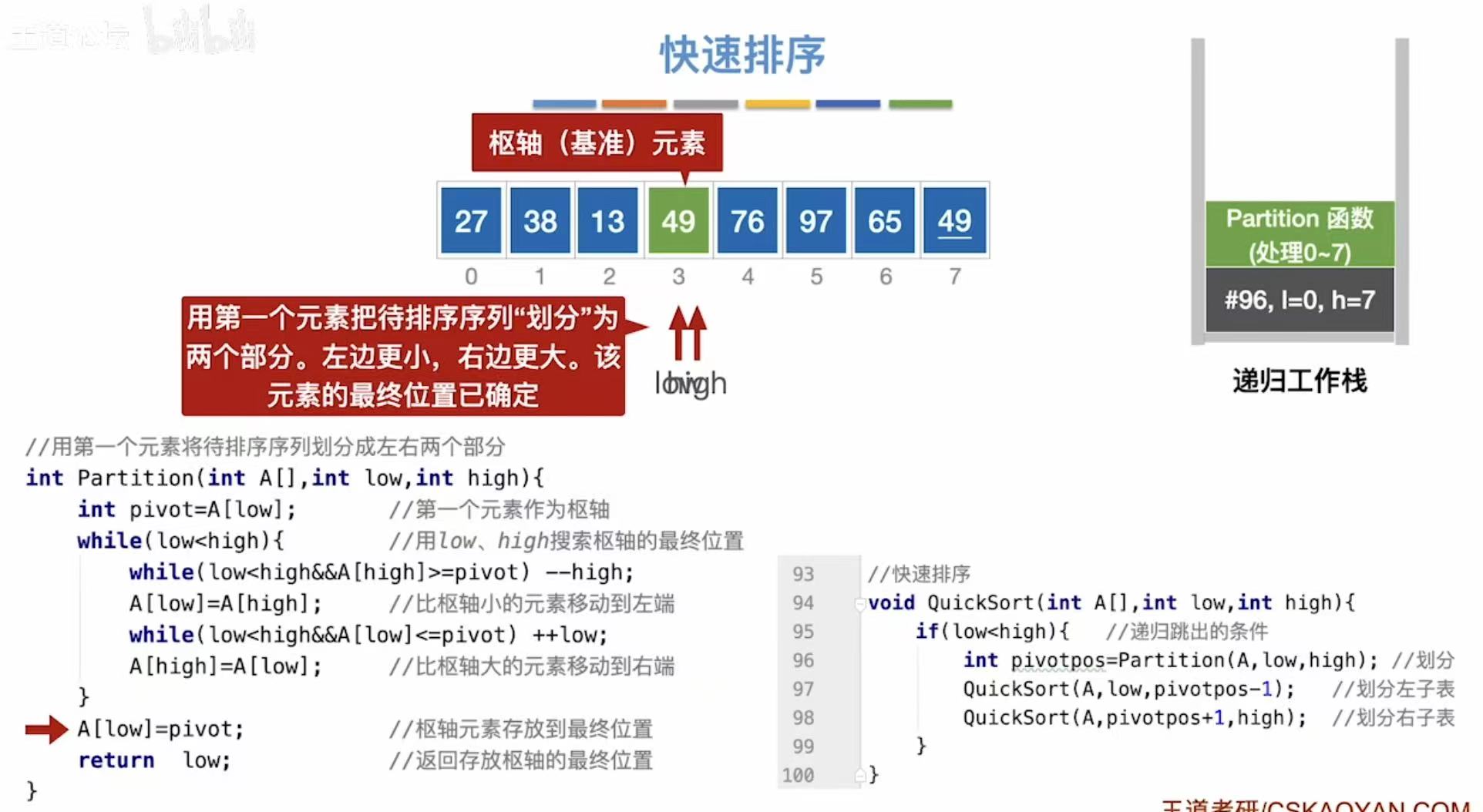
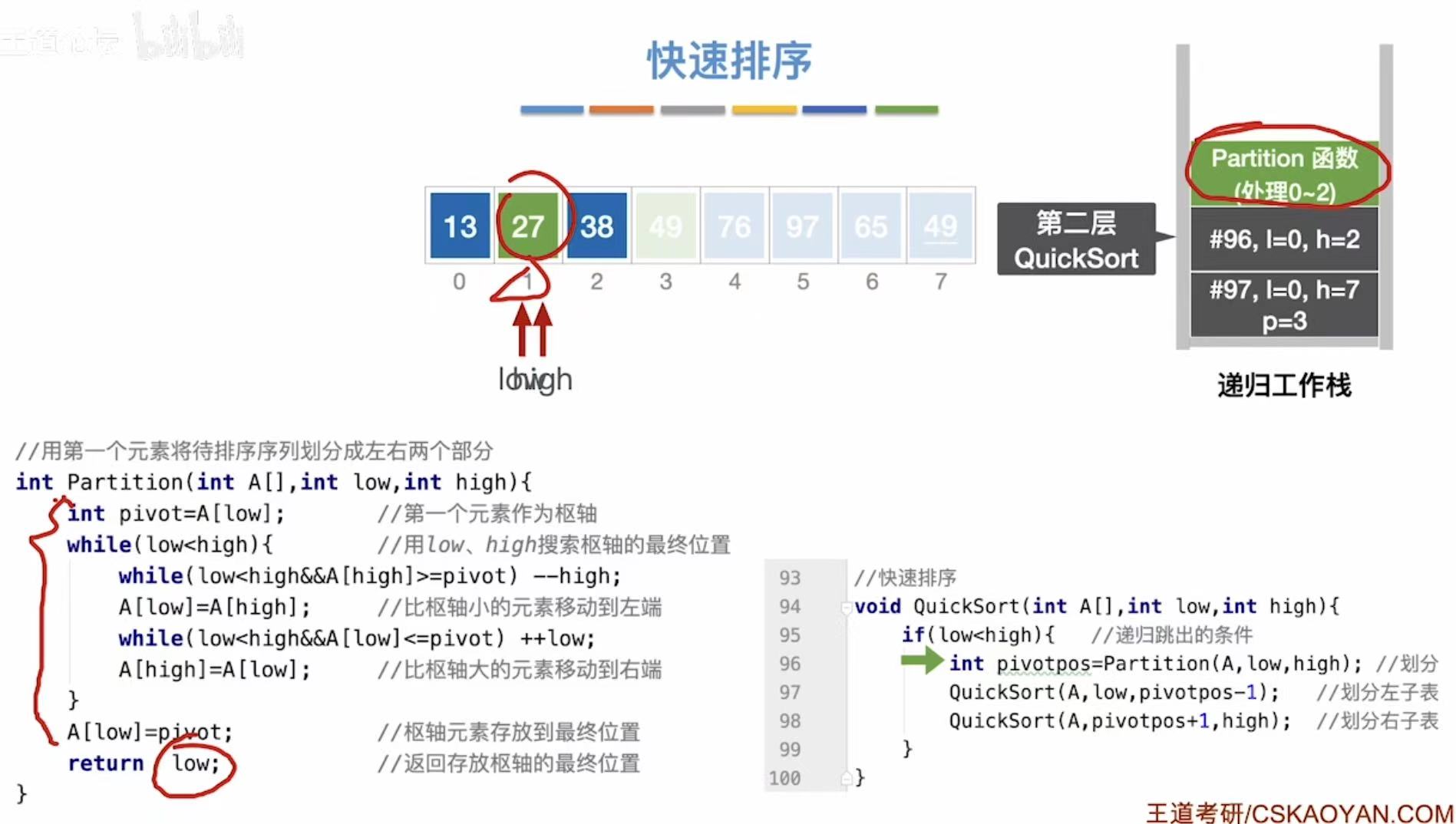
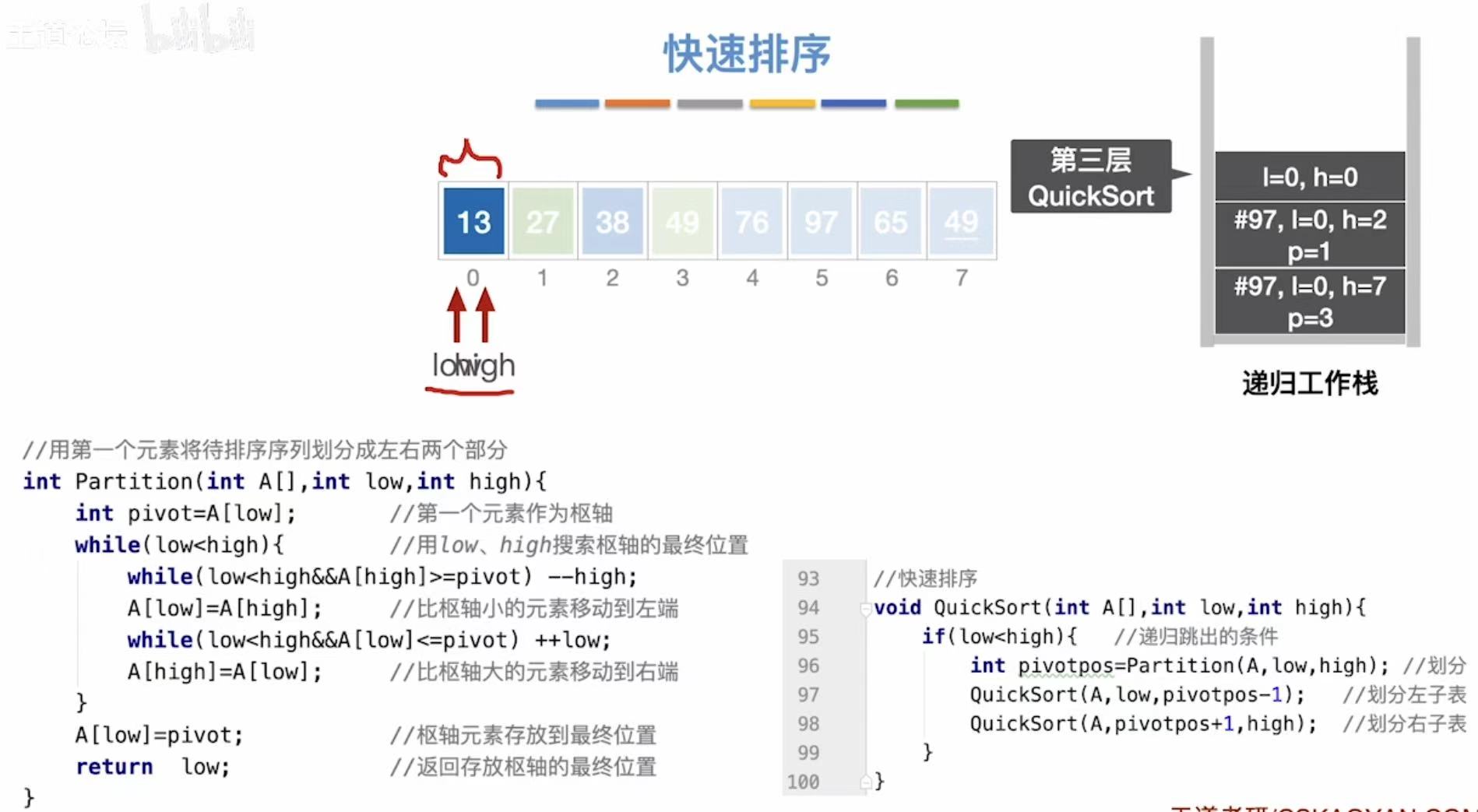
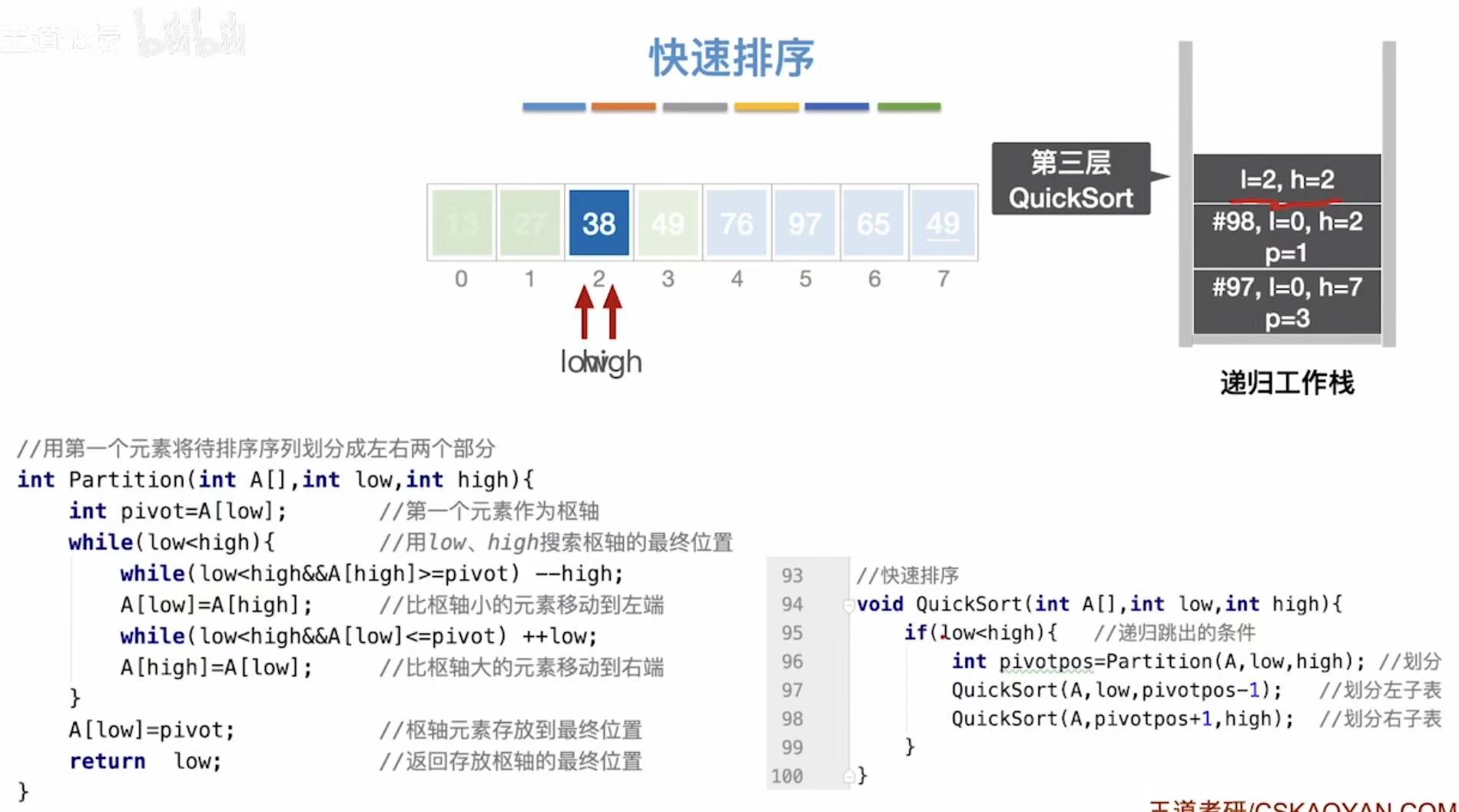
按照上述的逻辑，再次重复快速排序的步骤：

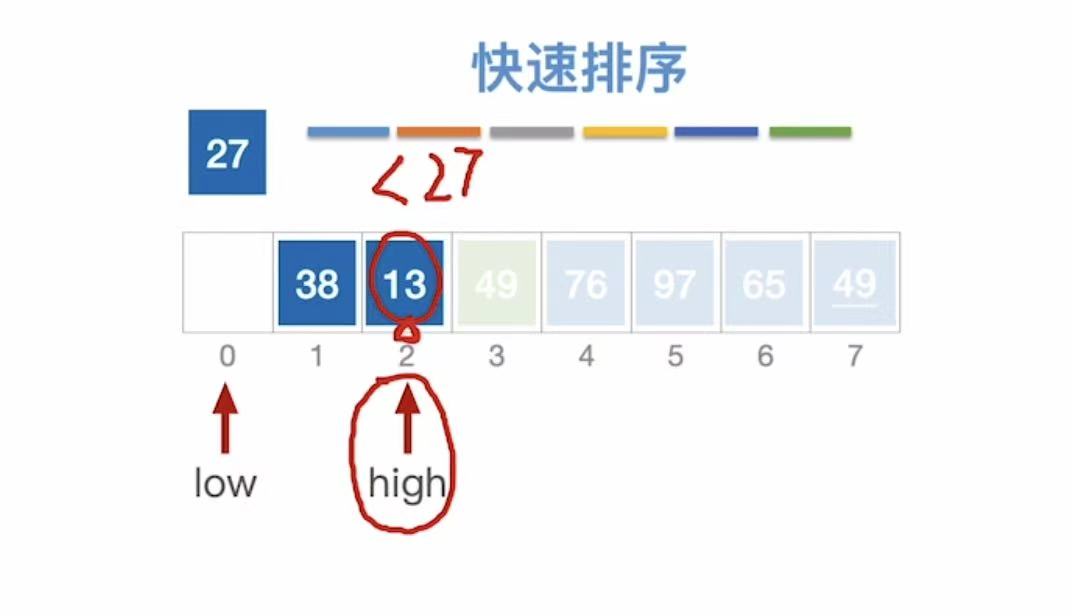
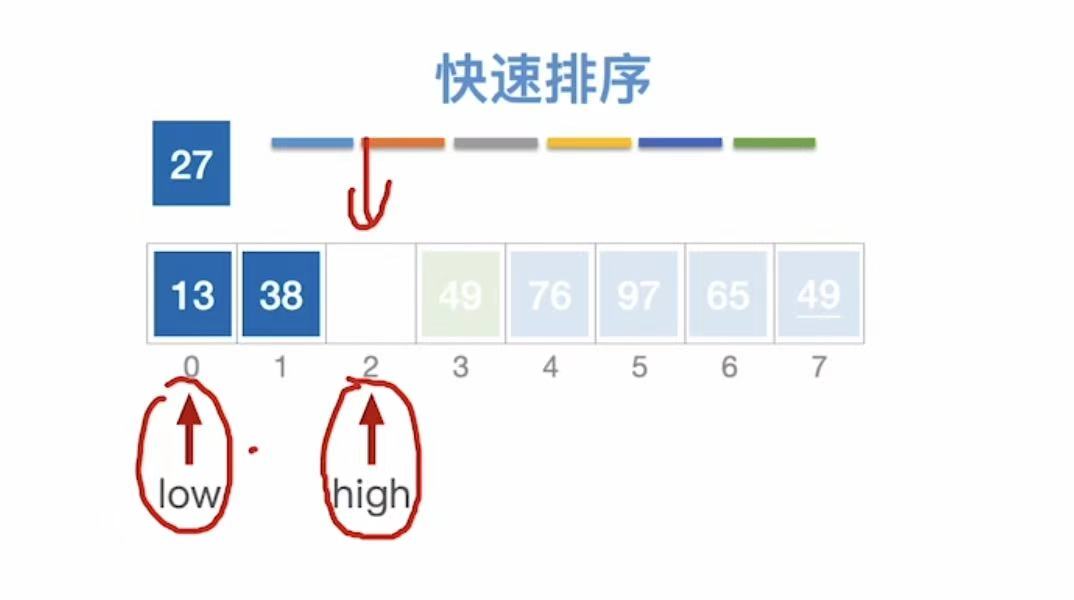
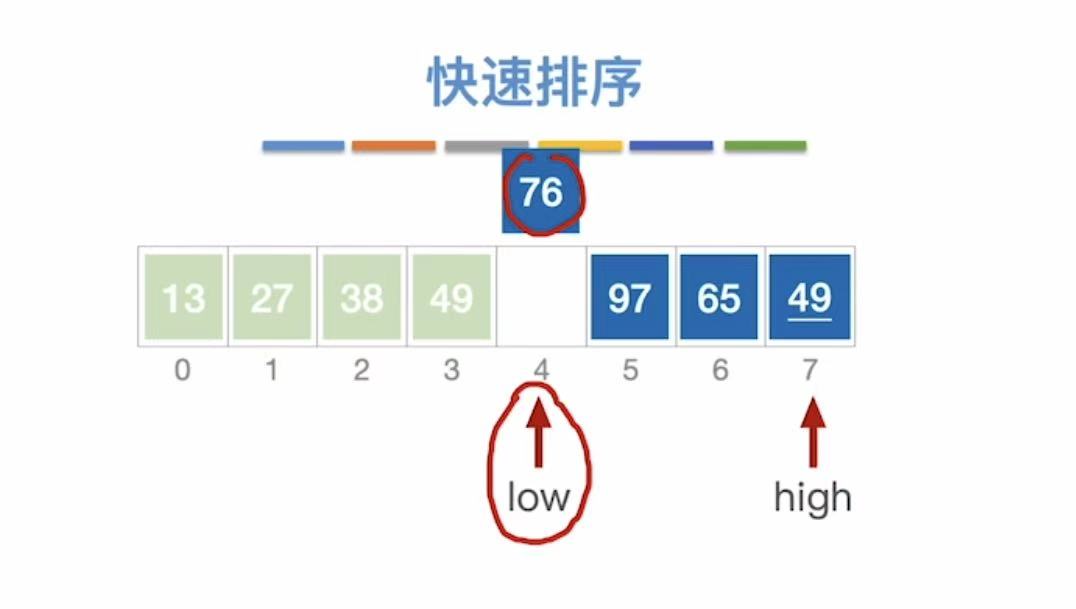
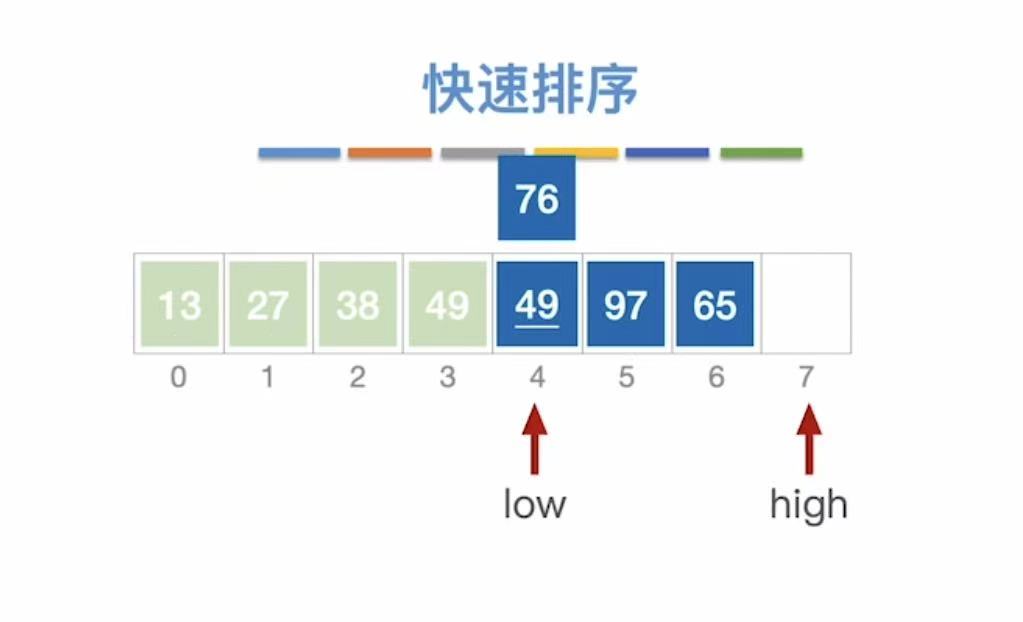
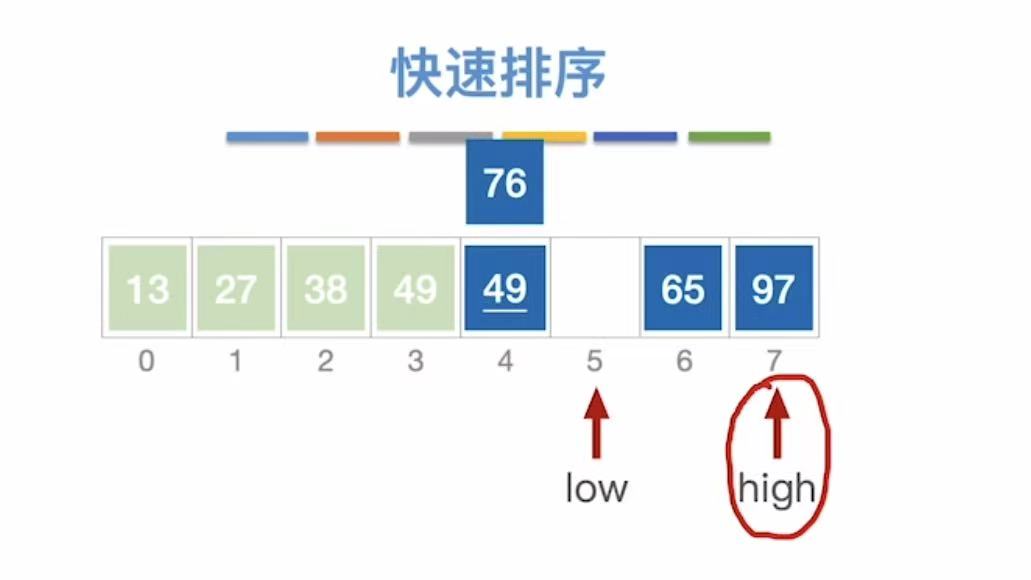
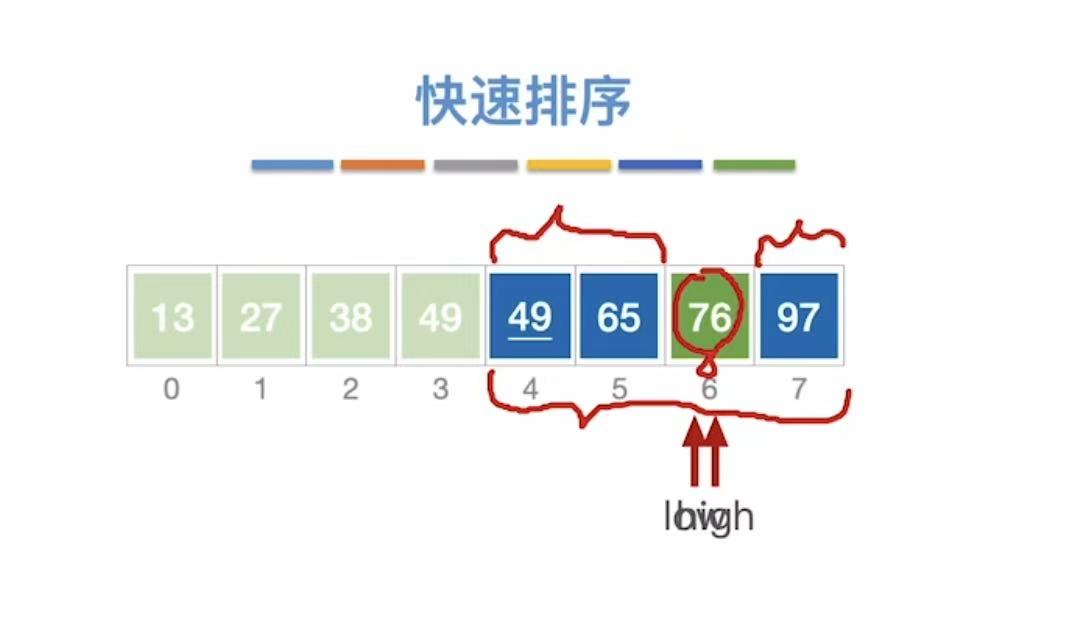
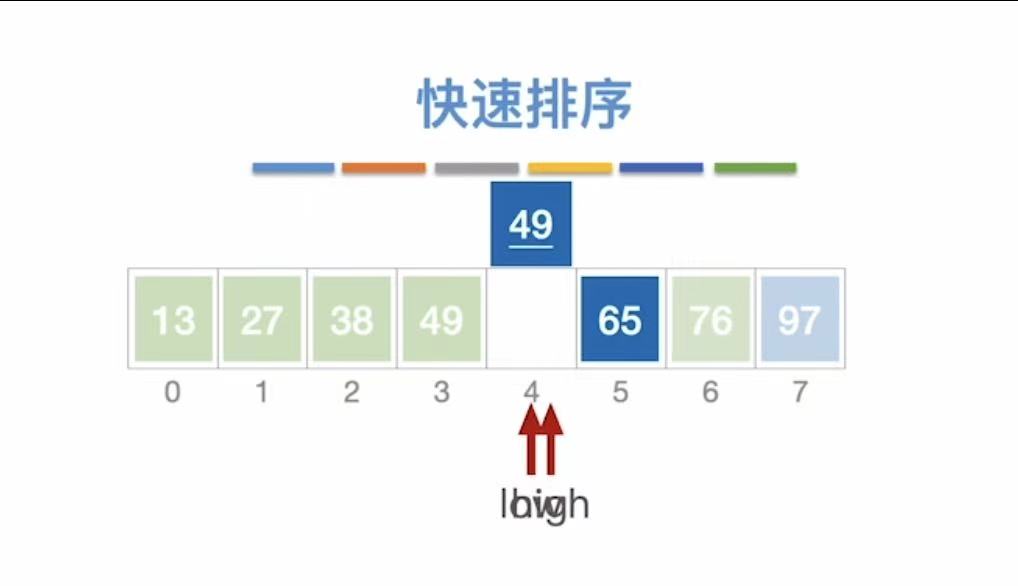
最终得到的结果：

3.2.2 算法实现

分区（Partition）：

java 复制代码

// 用第一个元素作为枢轴，将数组划分为左右两部分
int Partition(int A[], int low, int high) {
    int pivot = A[low];  // 将第一个元素 A[low] 作为枢轴（pivot）
    
    while (low < high) {  // 当 low 和 high 没有相遇时继续循环
        // 从右向左找：找到第一个小于 pivot 的元素
        while (low < high && A[high] >= pivot)
            high--;        // 右指针左移
        
        // 此时 A[high] < pivot，将其移到左边
        A[low] = A[high];  // 将较小值放到左端
        
        // 从左向右找：找到第一个大于 pivot 的元素
        while (low < high && A[low] <= pivot)
            low++;         // 左指针右移
        
        // 此时 A[low] > pivot，将其移到右边
        A[high] = A[low];  // 将较大值放到右端
    }
    
    // 最终 low == high，此时将原 pivot 放到正确位置
    A[low] = pivot;       // 枢轴元素放入最终位置
    
    return low;           // 返回枢轴的最终位置（即分割点）
}

快速排序（QuickSort）：

java 复制代码

// 快速排序：递归地对左右子数组进行排序
void QuickSort(int A[], int low, int high) {
    if (low < high) {     // 递归终止条件：当区间长度小于等于1时停止
        int pivotpos = Partition(A, low, high);  // 划分数组，返回枢轴位置
        
        // 递归排序左半部分（小于枢轴的元素）
        QuickSort(A, low, pivotpos - 1);
        
        // 递归排序右半部分（大于枢轴的元素）
        QuickSort(A, pivotpos + 1, high);
    }
}

栈深度	函数调用	low	high	操作说明
0	`Partition(0,7)`	0	7	处理整个数组，pivot = A[0] = 49
1	`QuickSort(0, pivotpos-1)`	0	3	左子表（小于等于 49 的部分）
2	`Partition(0,3)`	0	3	分割左子表，pivot = A[0] = 49
3	`QuickSort(0, pivotpos-1)`	0	1	更小的左子表
4	`Partition(0,1)`	0	1	分割
5	`QuickSort(0, pivotpos-1)`	0	-1	空区间，返回
6	`QuickSort(pivotpos+1, 1)`	1	1	单元素，终止
7	`QuickSort(pivotpos+1, 3)`	2	3	右子表
8	`Partition(2,3)`	2	3	分割
9	`QuickSort(2, pivotpos-1)`	2	1	空区间，返回
10	`QuickSort(pivotpos+1, 3)`	3	3	单元素，终止
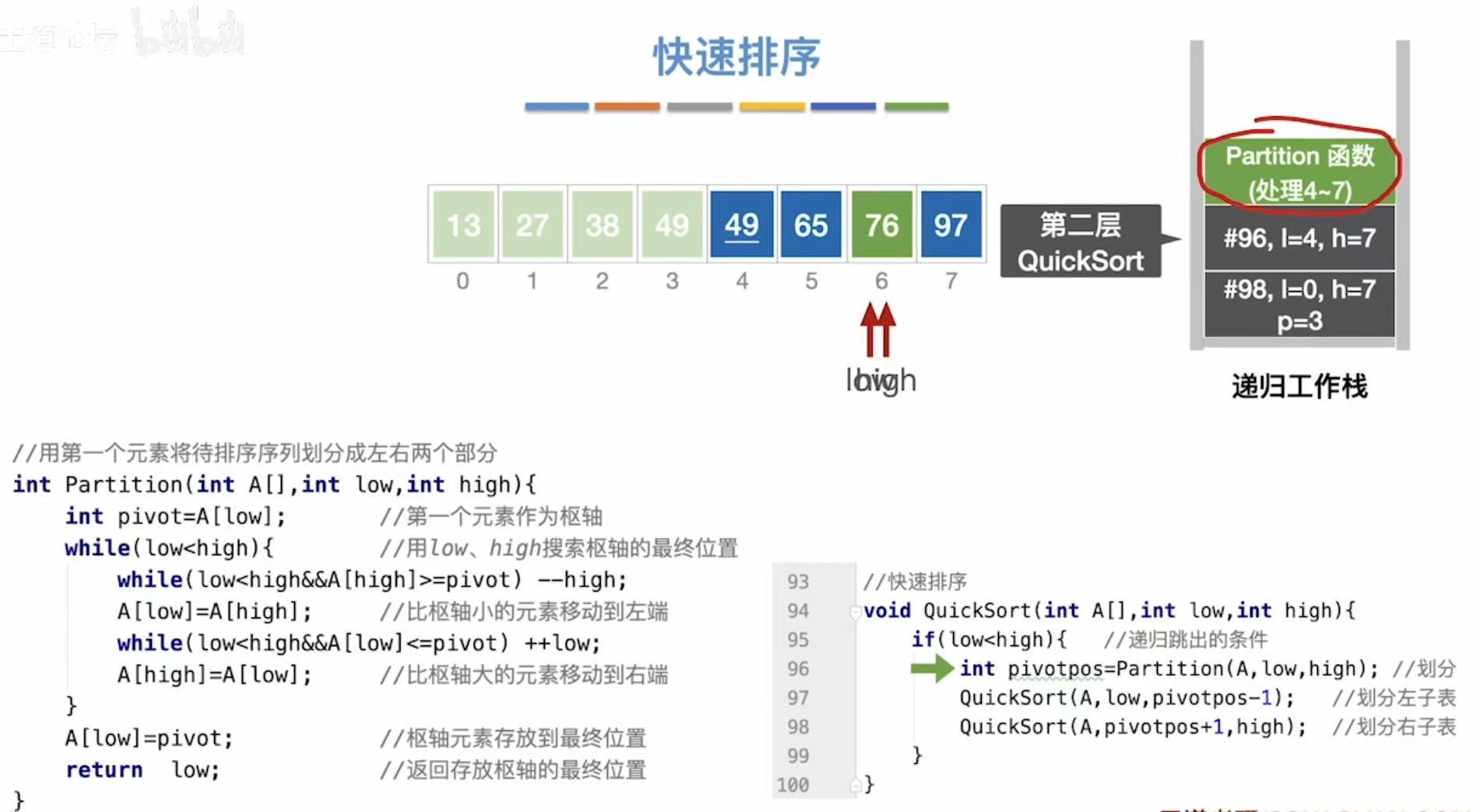
11	`QuickSort(pivotpos+1, 7)`	4	7	右子表（大于 49 的部分）
12	`Partition(4,7)`	4	7	分割，pivot = A[4] = 76
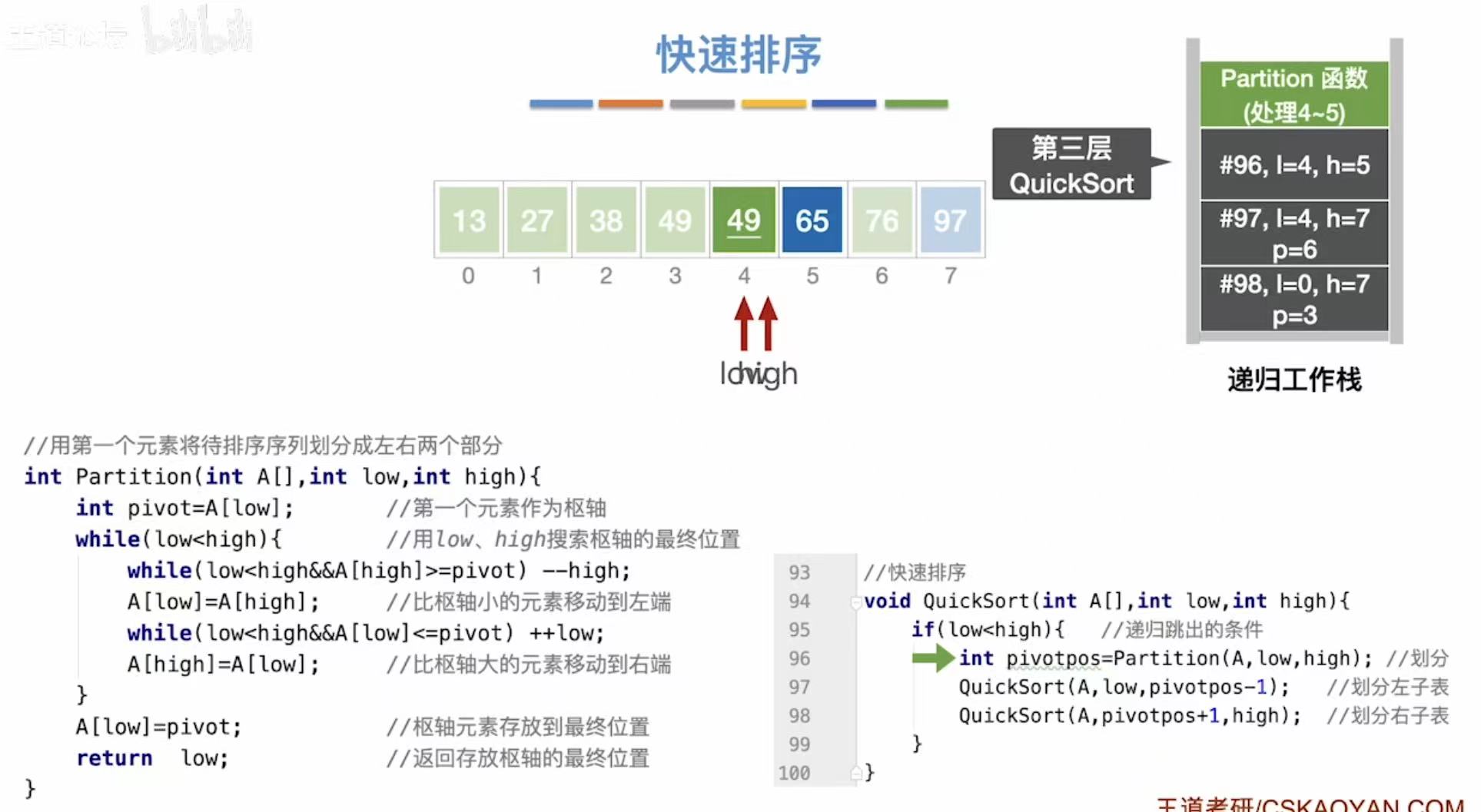
13	`QuickSort(4, pivotpos-1)`	4	5	左子表
14	`Partition(4,5)`	4	5	分割
15	`QuickSort(4, pivotpos-1)`	4	3	空区间，返回
16	`QuickSort(pivotpos+1, 5)`	5	5	单元素，终止
17	`QuickSort(pivotpos+1, 7)`	6	7	右子表
18	`Partition(6,7)`	6	7	分割
19	`QuickSort(6, pivotpos-1)`	6	5	空区间，返回
20	`QuickSort(pivotpos+1, 7)`	7	7	单元素，终止

考研408--数据结构--day15--排序&内部排序（上）

目录

排序

1. 什么是排序

2. 排序算法的应用

3. 排序算法的评价指标

4. 排序算法的分类

5. 小结

内部排序

1. 插入排序

1.1 算法思想

1.2 算法实现

1.3 算法效率分析

1.4 优化--折半插入排序

1.4.1 第一次查找

1.4.2 第二次查找

1.4.3 最终结果

1.4.4 稳定&代码

1.5 对链表进行插入排序

1.6 小结

2. 希尔排序

2.1 过程

2.1.1 第一趟

2.1.2 第二趟

2.1.3 第三趟

2.1.4 小结

2.2 算法实现

2.3 算法性能分析

2.4 小结

3. 交换排序

3.1 冒泡排序

3.1.1 过程

3.1.1.1 第一趟

3.1.1.2 第二趟

3.1.1.3 第三趟

3.1.1.4 第四趟

3.1.1.5 第五趟

3.1.2 算法实现

3.1.3 算法性能分析

3.1.4 小结

3.2 快速排序

3.2.1 算法思想

3.2.2 算法实现

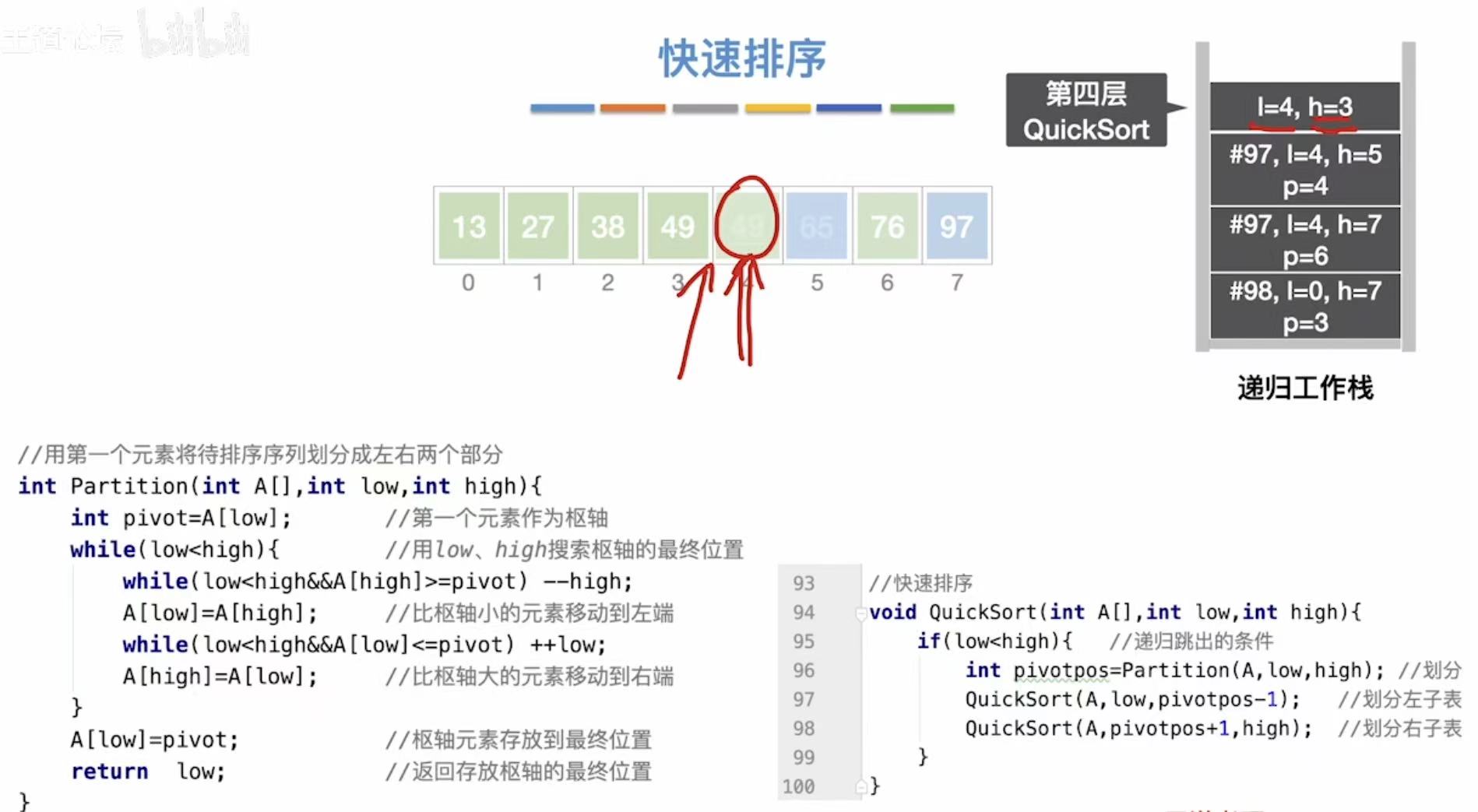
3.2.3 算法效率分析

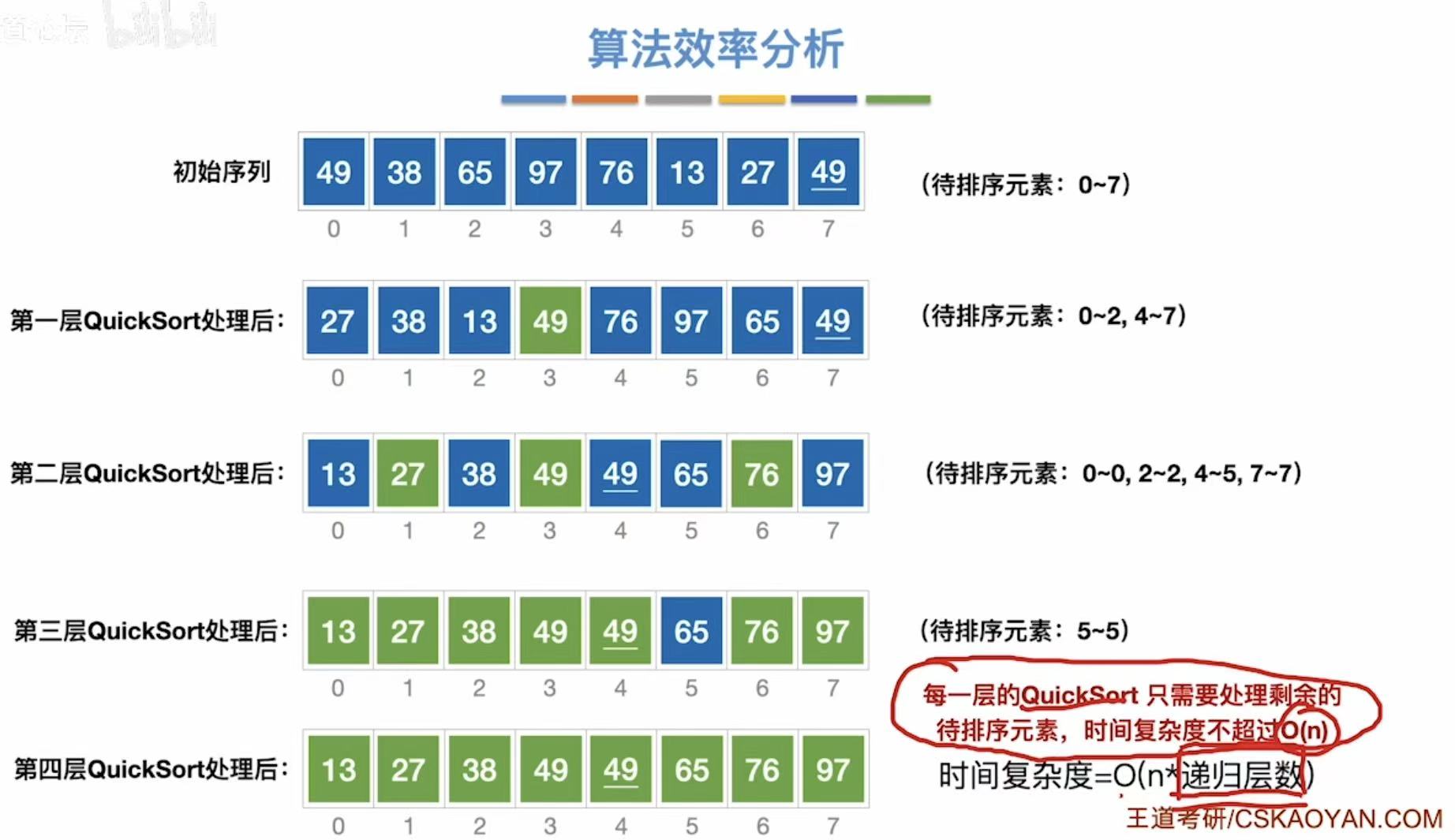
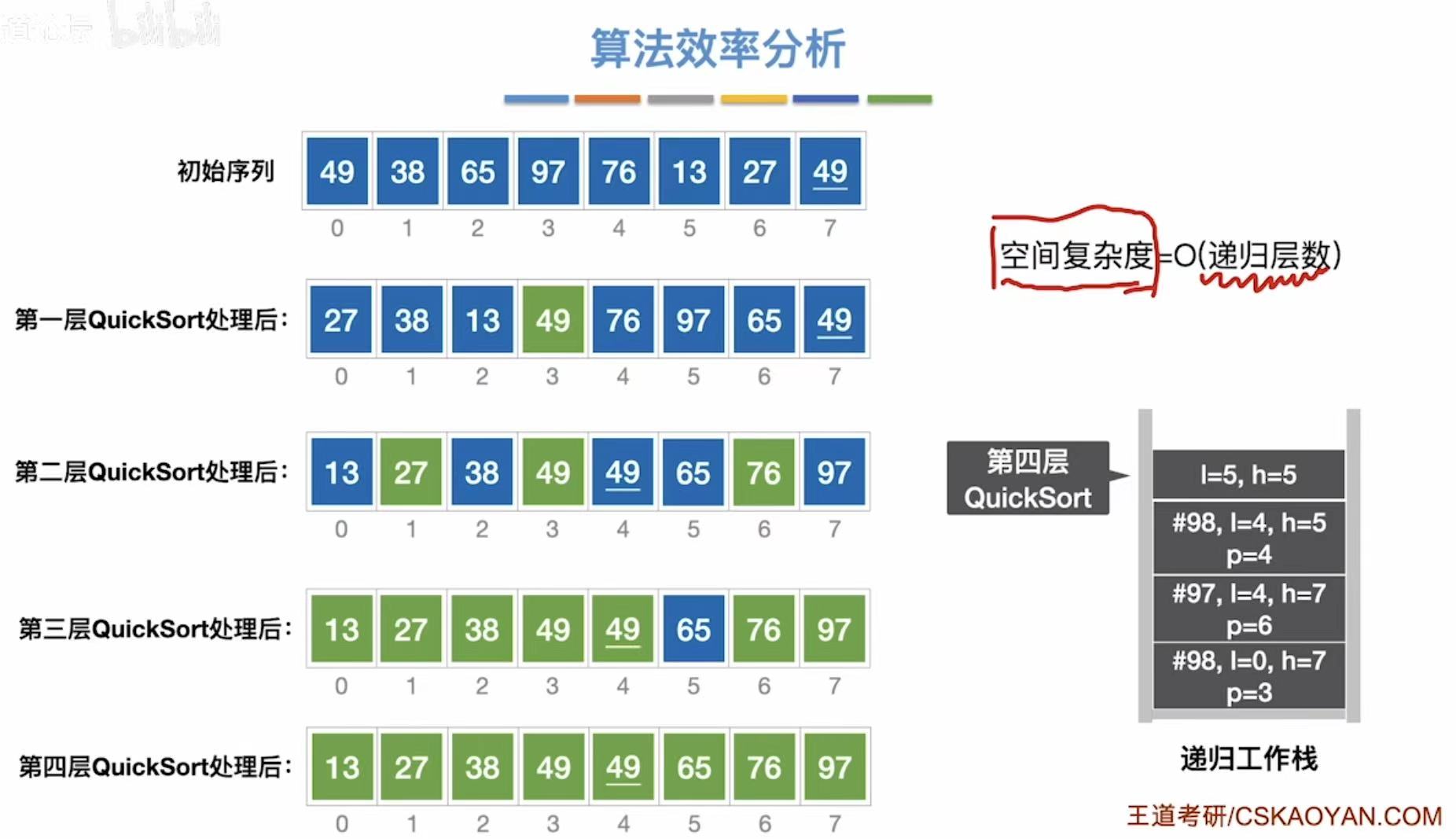
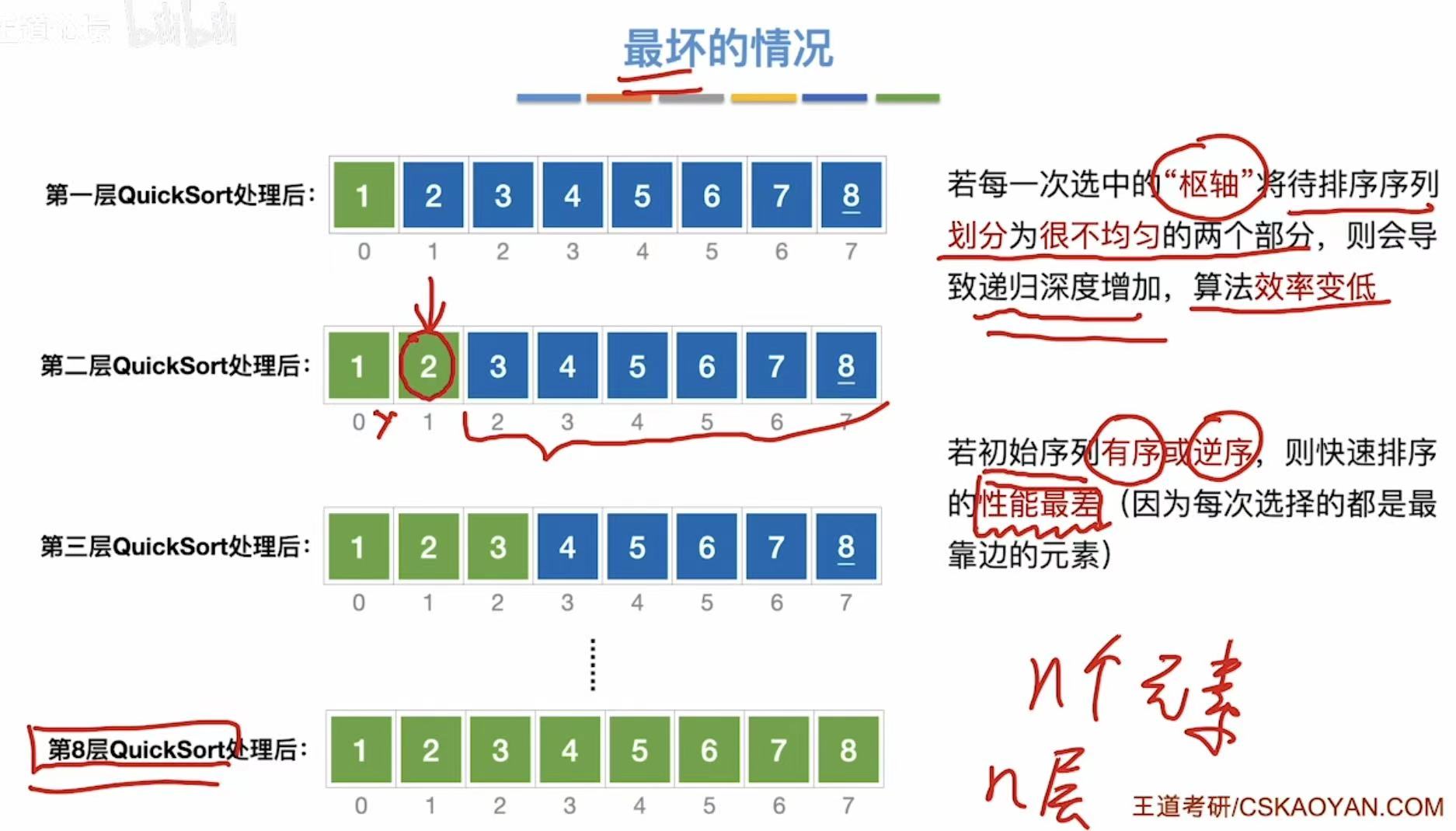
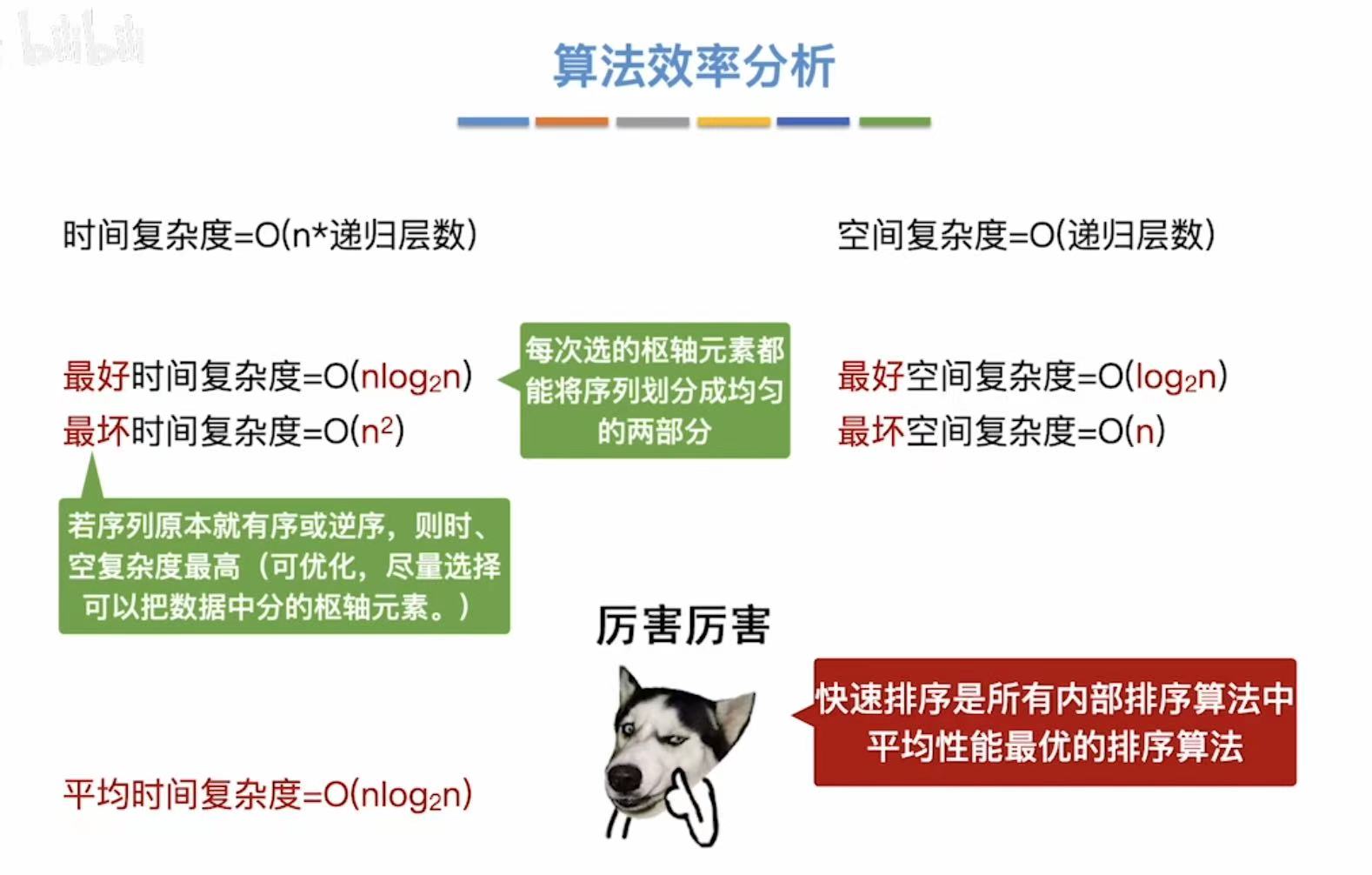
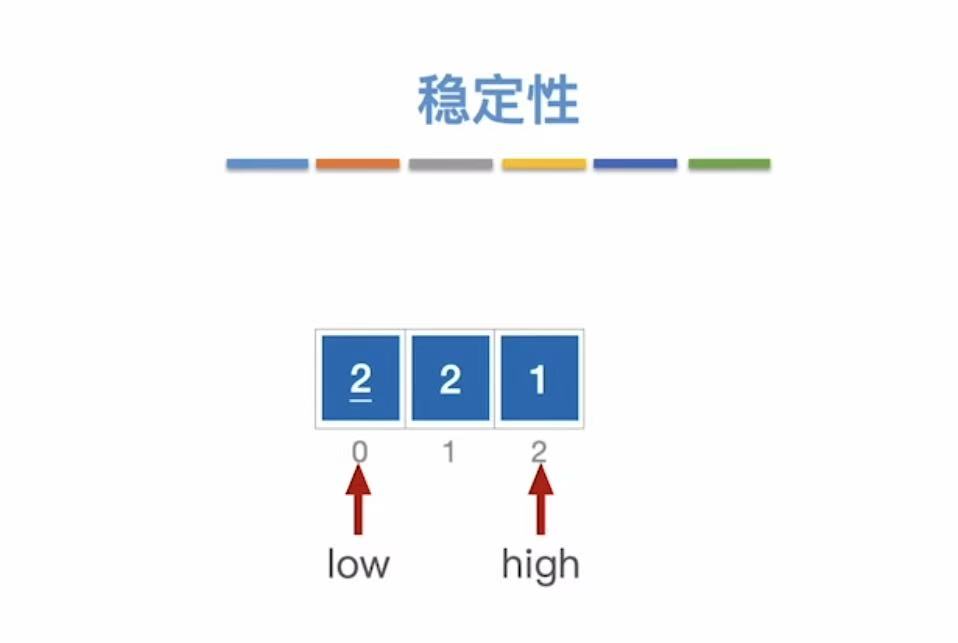
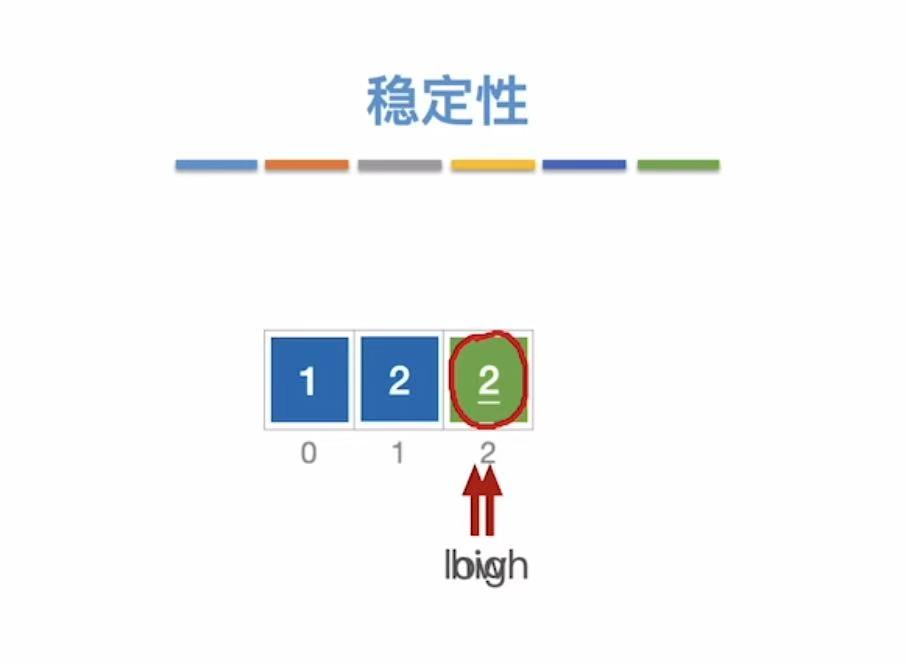
3.2.4 小结