目录
1.程序功能描述
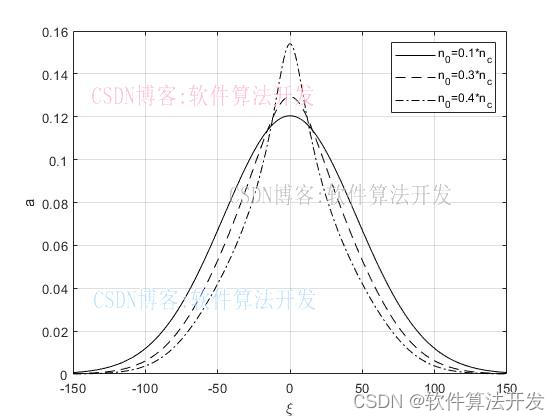
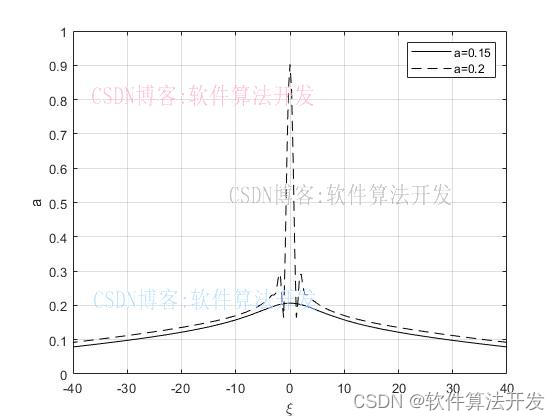
基于分步傅立叶数值算法的一维非线性薛定谔方程求解matlab仿真.
2.测试软件版本以及运行结果展示
MATLAB2022A版本运行

3.核心程序
....................................................................
%ssfm步长
d = 0.001;
M = S/d;
%输入脉冲
T0 = 70*tao;
a0 = 0.12;
%高斯脉冲
U = a0*exp(-(t/T0).^2/2);
U0 = U;
P0 = 1.77e7;
for m=1:1:M
U = exp(d*r*P0*i*(abs(U).*abs(U))).*U;
%对考虑了非线性后得到的结果进行fft变换
U = fftshift(fft(U));
%对上面的结果在频域内进行色散计算
U = exp(d*(i*B2*w2/2)).*U;
%再将结果转换到时域内
U = ifft(ifftshift(U));
end
hold on;
plot(1e2*t,abs(U),'k-.');
grid on;
xlabel('\xi');
ylabel('a');
legend('n_0=0.1*n_c','n_0=0.3*n_c','n_0=0.4*n_c');
16_025m4.本算法原理
分步傅立叶法是一种有效且广泛应用于求解 NLSE 的数值方法,它将非线性和扩散部分分开处理,利用傅立叶变换高效地求解线性部分。其基本思想是将时间演化分成小的时间步长Δt,并在每个时间步内,先线性地处理波动项(即施加傅立叶变换处理扩散),然后处理非线性项。具体步骤如下:


本课题的方程为:
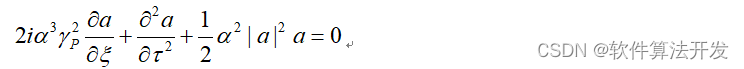
从对比可知,这两个式子形式上是相同的,区别在于本课题的式子在标准式子基础上增加了系数。
一般情况下,常规的有有限差分法和分步傅立叶法,本文我们所使用的是分布傅立叶法,下面讲一下主要的步骤:
首先,上面的公式做如下的逐步转化:
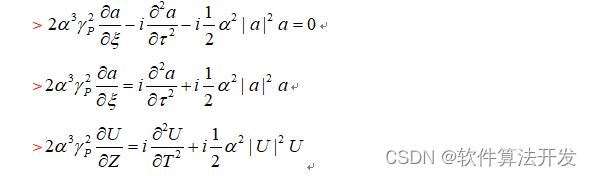
另外,从上面的式子可以看到,整个方程中U只和Z和T相关,其余均为常系数,或者是变常系数,但这U无关,那么我们简化上面的公式,把我们的公式变为标准非线性薛定谔的表现形式。


5.完整程序
VVV