数组 (原地处理数据不能使用Hash)
数组是存放在连续 内存 空间上的相同类型数据的集合。
数组可以方便的通过下标索引的方式获取到下标下对应的数据。
- 数组下标都是从0开始的。
- 数组 内存 空间的地址是连续的
正是因为数组的在 内存 空间的地址是连续的,所以我们在删除或者增添元素的时候,就难免要移动其他元素的地址 。

53 最大子数组和 (动归 普通数组部分)
给你一个整数数组 nums ,请你找出一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
子数组是数组中的一个连续部分。
贪心算法 :如果之前的数组和为负数,那么只选取当前数字作为结果会更大
class Solution {
public int maxSubArray(int[] nums) {
// 贪心算法
int max = Integer.MIN_VALUE;
int sum = 0;
for (int num : nums) {
sum = sum > 0 ? sum + num : num;
max = Math.max(max, sum);
}
return max;
}
}56 合并区间(贪心)
以数组 intervals 表示若干个区间的集合,其中单个区间为 intervals[i] = [start(i), end(i)] 。请你合并所有重叠的区间,并返回 一个不重叠的区间数组,该数组需恰好覆盖输入中的所有区间 。
class Solution {
//贪心算法
public int[][] merge(int[][] intervals) {
List<int[]> res=new LinkedList<>();
//按照左边界进行排序
Arrays.sort(intervals,(x,y)->Integer.compare(x[0],y[0]));
int start=intervals[0][0];
int right=intervals[0][1];
for(int i=1;i<intervals.length;i++){
if(intervals[i][0]>right)
{
//没有重叠部分,输出当前区间
res.add(new int[]{start,right});
//更新坐标
start=intervals[i][0];
right=intervals[i][1];
}
else{
//有重叠部分,更新右边界
right=Math.max(right,intervals[i][1]);
}
}
res.add(new int[]{start,right});
return res.toArray(new int[res.size()][]);
}
}189 轮转数组(数学问题)
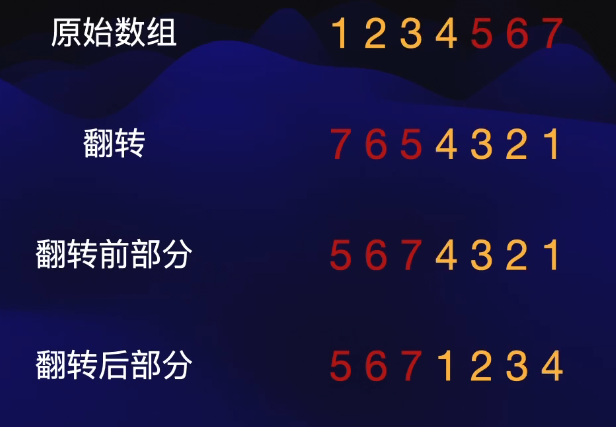
给定一个整数数组 nums,将数组中的元素向右轮转 k个位置,其中 k是非负数。
class Solution {
public void rotate(int[] nums, int k) {
// 三次翻转 1.全部翻转 2.翻转(0,k-1)3.(k,nums.length-1) 可以自己模拟一下
k %= nums.length;
reverse(nums, 0, nums.length - 1);
reverse(nums, 0, k - 1);
reverse(nums, k, nums.length - 1);
}
public void reverse(int[] nums, int s, int e) {
//双指针
while (s < e) {
int temp = nums[s];
nums[s] = nums[e];
nums[e] = temp;
s++;
e--;
}
}
}
public class Solution {
public String rotateString(String s, int k) {
char[] array = s.toCharArray();
k = k % array.length; // 如果k大于字符串长度,取余数
reverse(array, 0, k - 1); // 反转前k个字符
reverse(array, k, array.length - 1); // 反转剩余字符
reverse(array, 0, array.length - 1); // 反转整个字符串
return new String(array);
}
private void reverse(char[] array, int start, int end) {
while (start < end) {
char temp = array[start];
array[start] = array[end];
array[end] = temp;
start++;
end--;
}
}
}238 除自身以外数组的乘积(前后缀和)
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。
题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。
请 不要使用除法, 且在 O(n) 时间复杂度内完成此题。

假设有一个数组nums = [2, 3, 4, 5],我们要计算除了自身以外的元素的乘积,不使用除法。
- 计算s1和s2数组:
s1从左到右的累积乘积:[2, 6, 24, 120]。例如,s1[2] = nums[0] * nums[1] * nums[2] = 2 * 3 * 4 = 24。
s2从右到左的累积乘积:[120, 60, 20, 5]。例如,s2[1] = nums[3] * nums[2] * nums[1] = 5 * 4 * 3 = 60。
- 计算结果数组res:
对于第一个元素res[0],因为它左边没有元素,所以其结果就是s2[1] = 60。
对于最后一个元素res[3],因为它右边没有元素,所以其结果就是s1[2] = 24。
对于中间的元素:
res[1] = s1[0] * s2[2] = 2 * 20 = 40。res[1]是nums[1]除了自身以外的乘积,即nums[0] * nums[2] * nums[3]。
res[2] = s1[1] * s2[3] = 6 * 5 = 30。res[2]是nums[2]除了自身以外的乘积,即nums[0] * nums[1] * nums[3]。
最终,结果数组res = [60, 40, 30, 24],每个位置上的值都是除了该位置上的nums元素外,其余元素的乘积。
class Solution {
public int[] productExceptSelf(int[] nums) {
int n = nums.length; // 数组的长度
int[] s1 = new int[n]; // s1数组用于存储从左到右的累积乘积
int[] s2 = new int[n]; // s2数组用于存储从右到左的累积乘积
// 初始化s1和s2的第一个和最后一个元素
s1[0] = nums[0];
s2[n - 1] = nums[n - 1];
// 从左到右计算s1的累积乘积
for (int i = 1; i < n; i++) {
s1[i] = nums[i] * s1[i - 1];
}
// 从右到左计算s2的累积乘积
for (int i = n - 2; i >= 0; i--) {
s2[i] = nums[i] * s2[i + 1];
}
int[] res = new int[n]; // 结果数组
// 对于数组的第一个元素,其结果就是s2[1],因为它左边没有元素
res[0] = s2[1];
// 对于数组的最后一个元素,其结果就是s1[n-2],因为它右边没有元素
res[n - 1] = s1[n - 2];
// 对于数组中间的元素,其结果是它左边所有元素的乘积(s1[i-1])乘以它右边所有元素的乘积(s2[i+1])
for (int i = 1; i < n - 1; i++) {
res[i] = s1[i - 1] * s2[i + 1];
}
return res; // 返回结果数组
}
}另一种写法
这种方法的时间复杂度是O(n),因为它只需要两次遍历数组(一次前向,一次后向)。空间复杂度也是O(n),因为需要两个额外的数组(res和g)来存储结果和后缀累积乘积。
-
初始化结果数组 res:创建一个与输入数组nums长度相同的数组res,用于存储最终结果。
-
创建后缀累积乘积数组 g:创建一个长度为n + 1的数组g,其中n是nums数组的长度。g数组将存储从每个索引到数组末尾的元素乘积。初始化g[n]为1,因为数组末尾的元素右边没有更多元素,所以它的后缀乘积是1。
-
计算后缀累积乘积:从nums数组的倒数第二个元素开始,逆序遍历nums数组,计算每个索引i处的后缀累积乘积g[i]。g[i]的值是nums[i]乘以g[i + 1],即当前元素与它右边所有元素的乘积。
-
计算前缀累积乘积并填充结果数组 res:使用变量pre来跟踪从数组开头到当前索引的累积乘积。对于res中的每个索引i,计算res[i]的值,它是pre(区间[0, i-1]的乘积)乘以g[i + 1](区间[i+1, n-1]的乘积)。这样,res[i]就得到了除了nums[i]之外所有元素的乘积。
-
返回结果数组 res:最终,res数组包含了每个索引处除了该索引元素之外所有元素的乘积。
class Solution {
public int[] productExceptSelf(int[] nums) {
int n = nums.length;
int[] res = new int[n];
int[] g = new int[n + 1];//后缀 有效索引 0-n
g[n] = 1; // 后缀数组,表示[i, n-1]区间的乘积 最后一位(当前元素)右边没有元素,乘积设置为1
for (int i = n - 1; i >= 0; i--) {
g[i] = g[i + 1] * nums[i];
}
int pre = 1; // 表示区间[0, i-1]区间的乘积 求前缀乘积的时候顺便求了res 刨去当前元素
for (int i = 0; i < n; i++) {
res[i] = g[i + 1] * pre;
//先更新res,再更新pre 就是使用的[0,i-1]
pre *= nums[i];
}
return res;}}
矩阵(二维数组)

73 矩阵置零
给定一个 m x n 的矩阵,如果一个元素为 0 ,则将其所在行和列的所有元素都设为 0 。请使用 原地 算法**。**
我们可以用两个标记数组分别记录每一行和每一列是否有零出现。
具体地,我们首先遍历该数组一次,如果某个元素为 0,那么就将该元素所在的行和列所对应标记数组的位置置为 true。最后我们再次遍历该数组,用标记数组更新原数组即可。
时间复杂度是O(m*n),其中m是矩阵的行数,n是矩阵的列数,因为矩阵被遍历了两次。
空间复杂度是O(m+n),这是因为我们使用了两个额外的布尔数组来存储行和列的标记信息。
class Solution {
public void setZeroes(int[][] matrix) {
// 获取矩阵的行数和列数
int m = matrix.length, n = matrix[0].length;
// 创建两个布尔数组,分别标记哪一行和哪一列需要被置为0
boolean[] row = new boolean[m];
boolean[] col = new boolean[n];
// 第一次遍历矩阵,标记含0的行和列
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
// 检查当前元素是否为0
if (matrix[i][j] == 0) {
// 如果是0,标记所在的行和列
row[i] = col[j] = true;
}
}
}
// 第二次遍历矩阵,根据标记的行和列来设置0
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
// 如果行或列被标记为需要置0,就将当前元素设置为0
if (row[i] || col[j]) {
matrix[i][j] = 0;
}
}
}
}
}48 旋转图像
先把二维矩阵沿对角线反转,然后反转矩阵的每一行,结果就是顺时针反转整个矩阵。
class Solution {
public void rotate(int[][] matrix) {
int n = matrix.length;
// 先沿对角线反转二维矩阵
for (int i = 0; i < n; i++) {
for (int j = i; j < n; j++) {
// swap(matrix[i][j], matrix[j][i]);
int temp = matrix[i][j];
matrix[i][j] = matrix[j][i];
matrix[j][i] = temp;
}
}
// 然后反转二维矩阵的每一行
for (int[] row : matrix) {
reverse(row);
}
}
// 反转一维数组
void reverse(int[] arr) {
int i = 0, j = arr.length - 1;
while (j > i) {
// swap(arr[i], arr[j]);
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
i++;
j--;
}
}
}240. 搜索二维矩阵 II
编写一个高效的算法来搜索 m x n 矩阵 matrix 中的一个目标值 target 。该矩阵具有以下特性:
- 每行的元素从左到右升序排列。
- 每列的元素从上到下升序排列。
如果向左移动,元素在减小,如果向下移动,元素在增大
class Solution {
public boolean searchMatrix(int[][] matrix, int target) {
int m = matrix.length;
int n = matrix[0].length;
// 从右上角开始,规定只能向左或向下移动。
int i = 0, j = n - 1;
while (i < m && j >= 0) {
if (matrix[i][j] == target) {
return true;
} else if (matrix[i][j] < target) {
i++;
} else {
j--;
}
}
return false;
}
}59 螺旋矩阵II (模拟题目)
给定一个正整数 n,生成一个包含 1 到 n^2 所有元素,且元素按顺时针顺序螺旋排列的正方形矩阵。
示例:
输入: 3 输出: [ [ 1, 2, 3 ], [ 8, 9, 4 ], [ 7, 6, 5 ] ]
解题的核心思路是按照右、下、左、上的顺序遍历数组,并使用四个变量圈定未遍历元素的边界

upper_bound<=lower_bound // 上边界下移
从左往右遍历 <=
r<=l // 右边界左移
从上往下
u<=l // 下边界上移
从右往左
r<=l // 左边界右移
从下到上
class Solution {
public int[][] generateMatrix(int n) {
int[][] matrix = new int[n][n];
int upper_bound = 0, lower_bound = n - 1;
int left_bound = 0, right_bound = n - 1;
// 需要填入矩阵的数字
int num = 1;
while (num <= n * n) {
if (upper_bound <= lower_bound) {
// 在顶部从左向右遍历
for (int j = left_bound; j <= right_bound; j++) {
matrix[upper_bound][j] = num++;
}
// 上边界下移
upper_bound++;
}
if (left_bound <= right_bound) {
// 在右侧从上向下遍历
for (int i = upper_bound; i <= lower_bound; i++) {
matrix[i][right_bound] = num++;
}
// 右边界左移
right_bound--;
}
if (upper_bound <= lower_bound) {
// 在底部从右向左遍历
for (int j = right_bound; j >= left_bound; j--) {
matrix[lower_bound][j] = num++;
}
// 下边界上移
lower_bound--;
}
if (left_bound <= right_bound) {
// 在左侧从下向上遍历
for (int i = lower_bound; i >= upper_bound; i--) {
matrix[i][left_bound] = num++;
}
// 左边界右移
left_bound++;
}
}
return matrix;
}
}